Multivariate statistical techniques for the evaluation of groundwater quality of Amaravathi River Basin: South India

Abstract

The study of groundwater in Amaravathi River basin of Karur District resulted in large geochemical data set. A total of 24 water samples were collected and analyzed for physico-chemical parameters, and the abundance of cation and anion concentrations was in the following order: Na⁺ > Ca²⁺ > Mg²⁺ > K⁺ = Cl⁻ > HCO₃ ⁻ > SO₄ ²⁻. Correlation matrix shows that the basic ionic chemistry is influenced by Na⁺, Ca²⁺, Mg²⁺, and Cl⁻, and also suggests that the samples contain Na⁺–Cl⁻, Ca²⁺–Cl⁻ an,d mixed Ca²⁺–Mg²⁺–Cl⁻ types of water. HCO₃ ⁻, SO₄ ²⁻, and F⁻ association is less than that of other parameters due to poor or less available of bearing minerals. PCA extracted six components, which are accountable for the data composition explaining 81% of the total variance of the data set and allowed to set the selected parameters according to regular features as well as to evaluate the frequency of each group on the overall variation in water quality. Cluster analysis results show that groundwater quality does not vary extensively as a function of seasons, but shows two main clusters.

Introduction

Water is one of the most important natural resource for existence of lives and plants on the Earth. There are no other natural resources that have such an overpowering influence on human lives and plants (Sultanaa et al. 2017). Groundwater is a precious resource that India needs to utilize sustainably to meet the growing demands in its domestic, agricultural, and industrial divisions (Singh et al. 2013; Kumar et al. 2005). In the recent past, water demand of the river basin has been raised hastily by rising population and industrial activities; and it has led to serious exploitation of the available water resources. Meanwhile, the unplanned disposal of the anthropogenic wastes has resulted an undue accumulation of pollutant into waterway and terrain surface, and the successive leaching of the pollutants has caused the significant degradation of water quality of surface and shallow groundwater of the river basin. As a result, there is increasing trust to the depth groundwater resource as an option, safe, and consistent water source. However, knowledge on deep groundwater quality is limited and there is a lack of the complete study on deep groundwater quality (Chapagain et al. 2010).

Karur is a major textile center and has five major product groups, namely bed linens, kitchen linens, toilet linens, table linens, and wall hangings. An earlier survey in 2011 says that the total number of factories located on the banks of the Amaravathi River is about 515. The dyeing industry consumes totally 3225 L of water per day for dyeing process. About 14,600 m³ of coloured effluent with TDS 5000–10,000 mg/L is let into the Amaravathi River daily. Big factories had even dug tube wells to a depth of 275 m and discharged effluents into these wells lead to contamination of groundwater in the area. Soil turned infertile, the yield of the crops came down, slowly the farmlands became barren, and 250 open wells get contaminated. Kidney disorders, cancer, and abortion are high in the affected villages, revealed by local natives. Owing to zero discharge of effluents, in 2011, 459 dyeing units were closed and only 54 factories were given permission after they installed ETP (Suchitra 2014).

Recent news (Asha 1998) have driven scientists to look at the problems faced by the general public and farmers who use the groundwater for drinking, bathing, washing, agriculture, etc. Rajamanickam and Nagan (2010) have revealed that the Amaravathi River has been converted as drainage for industrial and domestic effluents. It is also reported 126 that the water quality parameters have been well above the permissible limits suggested by WHO (1977). Sivakumar et al. (2011) quantified that groundwater quality parameters of the Amaravathi River basin were crossing the permissible limits due to industrial and textile industrial activities. Similar results were reported by Raja and Venkatesan (2010) that the groundwater in Punnam village of Karur district is highly polluted due to the release of textile industries effluent. Understanding the nature of the factors influencing the groundwater composition in addition to identify them quantitatively, conventional graphical and multivariate statistical analysis was applied on hydrogeochemical statistics consisting of 24 different groundwater samples collected from Amaravathi River Basin, Tamilnadu, India.

Correlation matrix analysis is a valuable tool in hydrogeochemical studies that can specify the associations among individual parameters and thus enlightening the overall prudence of data set and enlightening the links between individual parameters and various controlling factors (Li et al. 2013; Wang and Jiao 2012). A correlation coefficient of < 0.5 exhibits poor correlation, 0.5 represents the good correlation, and > 0.5 highlights the excellent correlation (Vasanthavigar et al. 2013). Pearson’s correlation coefficient provides the elemental relationships between the original variables, which are presented in non-parametric form. Component analysis is a multivariate statistical technique which can be used for reducing complications of input variables when there is a large volume of information and it is anticipated to have an enhanced explanation of variables (Noori et al. 2010). It was used to identify the potential sources of major ions and trace metals, and to verify and quantify interrelationships among the real variables in a data set (Chen et al. 2007). CA is an unverified model recognition practice that classifies variables based on their associations. CA is considered to be a better approach than additional techniques such as principal component analysis, because it classifies the core factor in data without the requirement for some pre-assumption or a null hypothesis, and no simplification of data is required (Kumari et al. 2013). CA was used to determine the association between sampling sites, because it provides an indication of similarities/dissimilarities between the water quality parameters (Yang et al. 2014).

Physiographic setting

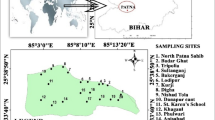
The river Amaravathi originates from Naimakad at an elevation of 2300 m above mean sea level in the Western Ghats in Idukki region of state Kerala (Fig. 1). The total length of the river is about 282 km, and it covers a total area of 8280 Km² mainly constituting five districts in Tamilnadu namely Coimbatore, Tirupur, Erode, Karur, and Dindigul. Amaravathi River in Karur lies between north latitudes 11.20° and 12.00° and east longitudes 77.28° and 78.50°. Amaravathi is a tributary of river Shanmuganadhi, Nankanchi, and Kodaganar, which joins at 60, 40, and 20 km upstream of Karur city, respectively. Amaravathi river reaches Karur district near Aravakurichi and joins with Cauvery River near Thirumakudalur village, and the water flow in the river is seasonal from late October to early February.

Fig. 1

Location map of the Amaravathi River basin showing sampling sites

Amaravathi River basin and sub-basin has four different seasons, namely summer season from March to May, southwest monsoon commencing from June to early September, northeast monsoon beginning of October to December, and winter season starting from January to February. The district receives the rain from both northeast and southwest monsoons. The northeast monsoon primarily contributes to the rainfall in the district. Precipitation habitually occurs in the form of cyclonic storms which is due to the effect of depressions in Bay of Bengal. The southwest monsoon rainfall is highly inconsistent, whereas summer rains are negligible. The average annual rainfall over the district from 1901 to 2011 varies between 620 and 745 mm, and in 2012, it was founded as 527.6 mm, much less than the states normal average rainfall of 652.20 mm (Renganathan 2014), and it is the least around Aravakurichi (622.7 mm) in the western region of the district. It progressively increases toward eastern parts and reach a maximum around Kulithalai (744.6 mm). The district enjoys a sub-tropical climate, and the relative humidities generally range from 40 to 80%. The average maximum temperature ranges from 26.7 to 38.56 °C, and the average minimum temperature ranged between 18.7 and 29.3 °C. The daylight heat is oppressive and the temperature attains high as 43.9 °C and the lowest temperature observed is 13.9 °C (CGWB 2008).

Completely, the entire area of the Karur district is a pediplain. Kadavur and Rangamalai hills occurring in the southern part of the district comprise the loose ends of the much denuded Eastern Ghats and rise to heights of over 1031 m above mean sea level. District possesses several small residual hills represented by Ayyarmalai, Thanthonimalai, and Velayuthampalayam hills. General altitude of the area is ranging between 100 m and 200 m above mean sea level. The well-known geomorphic units (Fig. 2b) known in the district are pediments, shallow pediments, buried pediments, structural hill, and alluvial plain (Ahamed et al. 2016).

Fig. 2

a–d Map showing the river, geomorphology, soil, and geology of the Karur district

Cauvery River drained the major parts of the Karur district. Amaravathi, Kodavanar, and Nanganji are the chief rivers draining the western region of the district and Pungar River drains in the eastern region of the district. The drainage pattern, generally, is dendritic. Except river Cauvery, all the rivers are seasonal and bring substantial flows during the monsoon time (Ahamed and Loganathan 2012).

Major part of the district is covered with red soil is the predominant one followed by red loam and thin red soil. Red soil is mostly seen in Kulithalai, Kadavur, Krishnarayapuram, Thogamalai, and Thanthoni blocks. Karur block is generally covered by red loam (Fig. 2c). The thin red soils are seen in K. Paramathy and Aravakurichi blocks. The major economic crops cultivated in this area are jowar (22.60%), paddy (16.30%), groundnut (6.90%), sugar cane (6.40%), and banana (5.30%). The total geographical area is 289,557 ha of which area employed in cultivation is 114,554, 37,264 ha land put into non-agricultural uses (Ahamed and Loganathan 2017) and the remaining are engaged in other activities (Table 1).

Table 1 Ninefold land-use/land-cover statistics for the district

The available data indicate that an area of about 54,709 ha, which is about 18.90% of the total geographical area of the district, is in irrigated agriculture. Dug wells accounting for about 59.97 percent of the total area irrigated in the district were the major source of water for irrigation. Tube wells account for about 9.48% of the total area irrigated in the district, while tank irrigation accounts only for 1.10%. Comparing the entire irrigation type, the canal irrigates only 29.45% area (Ahamed et al. 2015).

Geology and hydrogeology

The district is underlained entirely by Archaean Crystalline formations with fresh alluvial deposits taking place along the river and stream courses. The rigid consolidated crystalline rocks of Archaean age symbolize weathered, fractured, and fissured formations of gneisses, granites, charnockites, and additional related rocks (Fig. 2d). Deep groundwater occurs beneath phreatic conditions, and the most saturated thickness of the aquifer in rigid rock creation varied between 15 and 35 m depending upon the topographic circumstances (Ahamed et al. 2015). Thickness of the alluvial deposit is estimated to be approximately 10–12 m. The specific capacity of large diameter wells tested in crystalline rocks from 31 to 200 lpm/m of drawdown. The yield characteristics of wells vary considerably depending on the topographic set-up, lithology, and the degree of weathering. The seasonal fluctuation shows a rise in water level, which ranges from 0.46 to 1.98 m. The piezometric head varied between 3.53 and 5.34 m bgl during pre-monsoon and 2.04–7.59 m bgl during post-monsoon. The specific capacity in the weathered, partly weathered, and jointed rocks varies from 31 to 240.5 lpm/m/dd, and the transmissivity values in weathered, partly weathered, and jointed rocks vary from 15.5 to 154 m²/day. The optimum yield varied from 45.40 to 441.60 m³/day. The specific capacity in the fissured and fractured formation ranges from 6.89 to 117.92 lpm/m/dd, and the transmissivity values ranges from 11.42 to 669.12 m²/day. The specific capacity values in the porous formation vary from 135 to 958 lpm/m.dd and the transmissivity values ranged from 67.5 to 264.5 m²/day. The optimum yield varied from 232.8 to 549.6 m³/day.

Materials and methods

Sampling

Twenty-four groundwater samples were collected from bore and hand pumps during May (2013) and August (2013), representing the summer and pre-monsoon seasons, respectively. Bore wells and hand pumps for sampling were chosen on the base of an industrial unit in addition to diverse land-use patterns. Figure 1 represents the GIS map of the study area showing sampling locations. During sample collection, high-density white polyethylene bottles were used. The samples were filled up to the rim and were instantly preserved to avoid exposure to air, and were labeled scientifically. The labeled water samples were analyzed for their physico-chemical parameters in the laboratory. At sample collection for handling and preservation, the American Public Health Association (APHA 2005) standard procedures were followed to guarantee data quality and reliability.

Analytical procedures

The total dissolved solids (TDS), hydrogen ion concentration (pH), and electrical conductivity (EC) were determined immediately on location using water quality multi-tester probe (Eutech PC Tester 35), and the major ions were examined using the standard procedure suggested by the American Public Health Association (APHA 2005). Sodium (Na⁺) and potassium (K⁺) were determined by Flame photometer using Systronics make 128. Total hardness (TH), calcium (Ca²⁺), magnesium (Mg²⁺), bicarbonate (HCO₃ ⁻), and chloride (Cl⁻) were analyzed by volumetric methods following Trivedy and Goel methods, and sulphates (SO₄ ²⁻) were estimated by precipitation method using spectrophotometer. Fluoride ion concentration was estimated by ion selective electrode (Thermo scientific Orion 4 star). Phosphate and nitrate were examined by stannous chloride and brucine method using a spectrophotometer. The accurateness of the results was performed by calculating the ionic balance errors and it was usually within ± 5%.

Multivariate statistical analysis

Statistical analyses were carried out using SPSS software version 16.0. Karl Pearson correlation matrix analysis is a useful tool in hydrogeochemical studies that can indicate the associations between individual parameters and thus revealing the overall rationality of data set and enlightening the links between individual parameters and various controlling factors (Wang and Jiao 2012, Ahamed et al. 2017). A correlation coefficient of < 0.5 exhibits poor correlation, 0.5 represents the good correlation, and > 0.5 highlights the excellent correlation. Pearson’s correlation coefficient provides the elemental relationships between the original variables, which are presented in non-parametric form (Vasanthavigar et al. 2013). Two multivariate statistical techniques were employed, the PCA and the HCA. PCA is used for data reduction and for deciphering patterns within large sets of data. PCs provide information on the most meaningful parameters, which describes a whole data set affording data reduction with minimum loss of original information (Helena 2000). PCs were extracted on the symmetrical correlation matrix which consists of interrelations between variables; these PCs were subjected to varimax rotation (raw) generating. The HCA is a group of data classification technique; there are different clustering techniques; however, the hierarchical clustering is the one most widely useful in earth sciences (Davis 2002). Both Q-mode and R-mode were performed on the hydrochemical parameters. The Q-mode HCA was used to classify the samples into distinct hydrochemical groups, while the R-mode HCA is linking variables. To perform CA, an agglomerative hierarchical clustering was developed using a combination of the ward’s linkage method and squared Euclidean distances as a measure of similarity. The hydrochemical facies (Piper trilinear diagram) of the study area were plotted using AquaChem software version 4.0. GIS has emerged as a powerful tool for creating spatial distribution maps. The spatial analysis of various physico-chemical parameters was carried out using the ArcGIS v.9.3 software. To interpolate the data spatially and to estimate values between measurements, an inverse distance-weighed (IDW) raster interpolation technique was used (Srinivas et al. 2013). Analyzed results of May 2013 and August 2013 were presented in Tables 2 and 3.

Table 2 Physico-chemical characteristics of the groundwater samples (May 2013)

Table 3 Physico-chemical characteristics of the groundwater samples (August 2013)

Results and discussion

Groundwater chemistry and spatial distribution

The pH value indicates that the samples are faintly alkaline in nature (6.52–7.65), due to the collective effect of the high concentration of dissolved ions, variation in soil types, various aquifer systems, and anthropogenic activities, especially agricultural activities in the study area, and its spatial distribution is shown in Fig. 3a. The pH value of groundwater is mainly controlled by the amount of dissolved carbon dioxide, carbonate, and bicarbonate concentration (Zhou et al. 2013). An average TDS value of groundwater samples in the study area ranged between 2144 and 2101 mg/L (both seasons). None of the sample falls under “desirable for drinking” category, while 75% in both the seasons are suitable for irrigation and the remaining is out of condition for drinking and irrigational uses. Lower basin of the study area contains a high TDS value which may due to saline water intrusion and nutrient enrichment due to fertilizers could enhance TDS and, in turn, increases the EC in the lower basin. This is obviously shown in the spatial distribution map (Fig. 3b). The average value shows that the Ca²⁺ concentration exceeded the maximum allowable limit of 75 mg/L. Majority of the samples (90%) exposed higher concentration, comparing the upper and lower basin of the Amaravathi River; lower basin was mainly controlled by both weathering and anthropogenic activities to increase the concentration. The spatial distribution map of Ca²⁺ (Fig. 3c) clearly shows that samples from right side of the river basin exhibit higher value, which is highly influenced by dissolution process. The possible dissolution reaction of calcite and dolomite can be written as follows:

Fig. 3

a–d Spatial distribution of pH, TDS, Ca, and Mg in groundwater samples

$${\text{CaCO}}_{ 3} + {\text{ H}}_{ 2} {\text{CO}}_{ 3} \to {\text{ Ca}}^{ 2+ } + {\text{ 2HCO}}_{ 3}^{-} ,$$

(1)

$${\text{Ca}}\, \cdot \,{\text{Mg}}\left( {{\text{CO}}_{ 3} } \right)_{ 2} + {\text{ 2H}}_{ 2} {\text{CO}}_{ 3} \to {\text{ Ca}}^{ 2+ } + {\text{ Mg}}^{ 2+ } + {\text{ 4HCO}}_{ 3}^{-} .$$

(2)

The highest concentration of calcium, magnesium, chlorides, and bicarbonates in several cases may probably be due to their low rate of removal of soil (Ahamed et al. 2015). The mean magnesium value of groundwater samples from left and right sides of the river basin in both the seasons is between 78 and 92 mg/L. About 80% samples experienced higher value and only 20% samples possess value < 50 mg/L. The spatial distribution map shows that Mg²⁺ is found high in right side of the river basin covering upper and middle basin (Fig. 3d). From the correlation analysis, magnesium concentrations were not correlated with bicarbonate concentrations which specify that the suspension of calcite and dolomite is quite less when compared with halite and gypsum are the governing processes controlling water salinity. Gypsum suspension is the second resource of minerals in these waters subsequent to halite. The samples exceeding the acceptable limits might be due to the geology of the area. Magnesium usually occurs in less significant concentration than calcium owing to the fact that the dissolution of magnesium rich minerals is a slow process and that of calcium is additionally rich in the earth’s crust. If the concentration of magnesium in drinking water is in excess of the tolerable limit (30 mg/L), it causes an unpleasant taste to the water 187. Longer use of hard water may damage the kidney and resulted in de-functioning. Excess Mg²⁺ present in the groundwater will harmfully change the soil quality, converting it to alkaline and reduce crop yields (Ahamed et al. 2013).

The average value of Na⁺ was between 369 and 392 mg/L for left and right sides of the river basin in both the seasons. The maximum permissible limit of K⁺ in drinking water is 12 mg/L, and it is found that 45% of the samples in both seasons exceeded the limits of BIS (2003) and WHO (2005). Excess concentration of Na⁺ and K⁺ is supplied from the weathering of Na⁺ and K⁺ feldspar with carbonic acid by the following reactions:

$$2 {\text{NaAlSi}}_{ 3} {\text{O}}_{ 8} + {\text{ 2H}}_{ 2} {\text{CO}}_{ 3} + {\text{ 9H}}_{ 2} {\text{O }} \to {\text{ Al}}_{ 2} {\text{Si}}_{ 2} {\text{O}}_{ 5} \left( {\text{OH}} \right)_{ 4} + {\text{ 2HCO}}_{ 3} + {\text{ 2Na }} + {\text{ 4H}}_{ 4} {\text{SiO}}_{ 4} ,$$

(3)

$$2 {\text{KAlSi}}_{ 3} {\text{O}}_{ 8} + {\text{ 2H}}_{ 2} {\text{CO}}_{ 3} + {\text{ 9H}}_{ 2} {\text{O }} \to {\text{ Al}}_{ 2} {\text{Si}}_{ 2} {\text{O5}}\left( {\text{OH}} \right)_{ 4} + {\text{ 2HCO}}_{ 3} + {\text{ 2K }} + {\text{ 4H}}_{ 4} {\text{SiO}}_{ 4} .$$

(4)

Excess levels of Na⁺ fluctuated in the process, where Ca²⁺ and Mg²⁺ ions are exchanged with Na⁺. From the spatial distribution diagram (Fig. 4a), it clearly indicates that the rock type and weathering were important in the upper region, but the anthropogenic activities played a more significant role in downstream regions. The Na⁺ concentration increased abruptly at the stations near the dyeing industry, noticeably demonstrating that man-made activities mainly contributed to the increase of the cation. The runoff from agricultural activities and industrial wastes percolates into the groundwater and thus increases the K⁺ content. The silicate minerals present in the groundwater increase the concentration, but compared with Na⁺, the lowest concentration of K⁺ is due to the more resistance of potash feldspars to chemical weathering and is fixed on clay materials. Figure 4b obviously shows that K⁺ is uniformly distributed right through the entire study area. High Na⁺ and K⁺ concentrations are mainly due to their mineralogical origin in the soils. Weathering of feldspar and montmorillonite generates water soluble Na⁺ and K⁺ ions. In addition, cation exchange processes also contribute for high Na⁺ and K⁺ concentrations in the study area. The adequate intake for adults (19 → 70 years of age) is 4.7 g/day. This is equivalent to 78 mg/kg body weight per day for a 60 kg adult. Potassium intoxication by ingestion is rare, as potassium is quickly excreted in the absence of pre-existing kidney hurt and because large single doses generally induce nausea (WHO 2009).

Fig. 4

a–d Spatial distribution of Na, K, HCO_3, and Cl in groundwater samples

The HCO₃ ⁻ concentration in groundwater samples exceeded (both seasons) the allowable limit of 100 and 200 mg/L according to BIS (2003) and WHO (2005) guideline value. Weathering of silicate minerals such as anorthite, Na⁺ and K⁺ feldspar additionally increases the concentration of HCO₃ ⁻ in groundwater samples from the upstream of the Amaravathi River basin, and in the downstream (Fig. 4c), the relatively high concentration of HCO₃ ⁻ is due to the direct mixing of municipal sewages and industrial drainage from Karur region. The Cl⁻ concentration of groundwater samples in both the seasons is found above the acceptable limit. About 87% samples are not suitable for drinking purposes. Elevated amounts of Cl⁻ in water are usually taken as an indicator of pollution and considered as the foundation of groundwater contamination. Geologically significant sources of chloride are appetite, sodalite, connate waters, and hot springs. Higher concentration was observed in the downstream of the Amaravathi River Basin (Fig. 4d), mainly due to the surface overspill from farming land, sewage and municipal wastes, and effluents from dyeing and bleaching industries. Cl⁻ imparts a salty taste, and sometimes, higher consumption causes the critical for the development of essential hypertension, risk of stroke, left ventricular hypertension, osteoporosis, renal stones, and asthma in human beings (McCarthy 2004).

The permissible limit for F⁻ is 1 mg/L, where in the study area, 29% of samples in both the seasons exceeding the guideline value. Specifically, two samples (c and g) from right side of the river basin recorded higher F⁻ value between 2.0 and 4.0 mg/L. At this concentration, the teeth lose their shiny appearance and chalky black, gray, or white patches develop known as mottled enamel (Hussain et al. 2012). The reason behind for high value recorded in the study area was constituted of the fractured hard rock zone. Abnormal level of F⁻ in water is widespread in the fractured hard rock zone with pegmatite veins. Fluorite (CaF₂) and calcite (CaCO₃) both contain Ca²⁺, their solubilities are interdependent, as the resultant circumstances that lead to little calcite solubility can also cause high concentration of F⁻ in groundwater. The spatial distribution of F⁻ concentration in water samples from the Amaravathi river basin is shown in Fig. 5a. From this, hike value was observed in the central part of the study region. The concentration of SO₄ ²⁻ in groundwater samples collected from the left and right sides of the Amaravathi river basin varied between 179 and 209 mg/L. During the May 2013, 45.83% of samples exceed the guideline value of 200 mg/L, while in August 2013, it is 50%. The spatial distribution map (Fig. 5b) shows that the upper and lower parts of an entire basin highlighted high concentration of SO₄ ²⁻, except central basin. Conversely, SO₄ ²⁻ can be supplied by the oxidation of pyrite (geologic form), dyeing wastewater, fertilizers (anthropogenic activities), precipitation, and industrial sewage from the textile industry and pulp manufacturing processes. NO₃ ⁻ content in both the seasons comes under the acceptable limit of 45 mg/L, and the net average value of samples collected on the left and right sides of the Amaravathi river basin was 0.98 and 1.01 mg/L, respectively. The spatial distribution pattern (Fig. 5c) indicates that the samples are evenly distributed throughout the study area. In groundwater samples, the PO₄ ³⁻ concentration varied between 0.30 and 0.22 mg/L, the sample “F” (May 2013) exceeded the maximum permissible limit of 1 mg/L, indicated by Fig. 5d.

Fig. 5

a–d Spatial distribution of F, SO₄, NO_3, and PO₄ in groundwater samples

Hydrochemical facies

Durov (1948) plot was drawn by plotting the major ions as percentages of milli-equivalents in two base triangles. The total cations and the total anions are set equal to 100% and the data points in the two triangles are projected onto a square grid that lies perpendicular to the third axis in each triangle. Figure 6a showed that the water type in the study area is Na⁺–Cl⁻ and mixed Ca²⁺–Mg²⁺–Cl⁻ type. Left triangle demonstrates that the samples are strongly occupied in Na⁺ + K⁺ field rather than Ca²⁺ + Mg²⁺ field, while the upper diagram indicates that almost all the samples fall near Cl⁻ type, which explains the simple dissolution and evaporation dominance. From the square field, all the samples fall and move from middle side to right side of the square grid, express the simple dissolution or linear mixing, and reverse ion exchange mechanism, respectively.

Fig. 6

a, b Classification of groundwater based on the Durov and Piper Trilinear diagram

Piper (1944) proposed a modified trilinear diagram for understanding the hydrogeochemical regime of the study area. The diagram consists of three distinct fields, two triangular fields, and one diamond-shaped field (Fig. 6b). The triangular cationic field in May 2013 and August 2013 indicates that 79.17% of samples fall into no dominant type, and 8.33 and 12.50% samples are in Mg²⁺ and Na⁺ + K⁺ types, respectively. From the anionic triangle, 62.50% samples fall into Cl⁻ type and the remaining are in no dominant class. Most of the samples fall in Zone 4 of diamond-shaped field which indicates the predominance of mixed Ca²⁺–Mg²⁺–Cl⁻ type followed by Ca²⁺–Cl⁻ and Na⁺–Cl⁻ type.

Gibbs mechanism

The mechanism controlling the chemical composition of major dissolved salts in water and ascertained close relationships between aquifer lithology and water compositional chemistry was proposed by Gibbs (1970) through Gibbs diagram for major cations and anions. This diagram was employed to assess hydrochemical processes such as atmospheric precipitation dominance, rock weathering dominance, and evaporation–crystallization dominance by plotting the weight ratios of (Na⁺ + K⁺)/(Na⁺ + Ca²⁺) and Cl⁻/(Cl⁻ + HCO₃ ⁻) represented as a function of TDS. Figure 7 shows that 91.67% in May 2013 and August 2013 have a plot in the evaporation–crystallization field. Only 8.33% samples were falling on the rock weathering field, due to weathering of minerals and salt precipitation. However, evaporation–crystallization is the dominant field, indicating the secondary evaporation. Groundwater evaporation is a common phenomenon in the study region.

Fig. 7

Mechanism controlling the groundwater in the Amaravathi River Basin

Correlation coefficient

In summer season (May 2013), the groundwater chemistry is influenced by weathering/dissolution processes. Intensive weathering reaction enhances the major cations like Ca²⁺ and Mg²⁺ and Na²⁺ by secondary evaporation. Result shows a good positive (Table 4) correlation between EC and TDS, and also with TH (r = 0.712), Ca²⁺ (r = 0.821), Na⁺ (r = 0.917), Cl⁻ (r = 0.976), and moderate with Mg²⁺ (r = 0.654), they are derived from the weathering of silicate lithology and also due to geochemical behaviour during ionic mobilization. The high positive relation between TH with Ca²⁺ (r = 0.845), Mg²⁺ (r = 0.763), and Cl⁻ (r = 0.784) indicates that hardness in groundwater is due to each CaCl₂ and MgCl₂, and all the parameters show negative correlation with pH. Poor water quality is observed in the lower basin of the study area which is polluted by various sources like sewage, industrial effluents, dumping of agro and chemical wastes, and human wastes. During the pre-monsoon season of August 2013, results evidently indicate (Table 5) that EC and TDS show a high positive correlation (r = 1) which may be due to the fact that the conductivity increases as the ionic concentration increases. In this season, the groundwater ionic chemistry is influenced by both geochemical process and anthropogenic activities. Good agreement is observed as PO₄ ³⁻ vs NO₃ ⁻ (r = 1), PO₄ ³⁻ and NO₃ ⁻ vs F⁻ (r = 0.999), EC and TDS vs SO₄ ²⁻ (r = 0.502), SO₄ ²⁻ vs Na⁺ (r = 0.467), and SO₄ ²⁻ vs Cl⁻ (r = 0.463) demonstrate the possibilities of ion exchange and association of pyrite oxidation and gypsum, halite dissolution. However, the basic ionic chemistry is influenced by Na⁺, Ca²⁺, and Mg²⁺ which suggests that the samples belong to Na⁺–Cl⁻, Ca²⁺–Cl⁻, and mixed Ca²⁺–Mg²⁺–Cl⁻ types of water.

Table 4 Correlation coefficient matrix of major cations and anions of the study area—May 2013

Table 5 Correlation coefficient matrix of major cations and anions of the study area—August 2013

Principal component analysis

In May 2013 (summer season), based on eigenvalue greater than 1 (Fig. 8a), six PCs were extracted that accounted for 81.596% of the variance in the original data set (Table 6). The high positive and negative loadings of each variable from 1 to 6 PCs are given below Factor 1 EC, TDS, TH, Ca²⁺, Mg²⁺, Na⁺, and Cl⁻; Factor 2 temperature, K⁺, HCO₃ ⁻, COD, and negatively by PO₄ ³⁻; Factor 3 F⁻, PO₄ ³⁻, NO₃ ⁻, BOD, and negatively by DO; Factor 4 moderate by pH, PO₄ ³⁻, and negatively by COD; Factor 5 moderate by temperature, F⁻ and negatively by HCO₃ ⁻ and Factor 6 K⁺. PC1 represents that the variables have a common pattern dominated in groundwater, which accounted for 34.201% of the total variance of the data set. The positive good relation of EC, TDS, TH, Ca²⁺, Mg²⁺, and Na⁺ is due to the fact that the most of discharge from the phreatic aquifer takes place by evaporation; huge amounts of salt remain in the soil and accumulate in phreatic water. PC2 accounted for 13.120% of the total variance and highly loaded by K⁺, HCO₃ ⁻, and temperature, which implies that PC2 related to contamination from agricultural inputs with the use of chemical manures like NPK, potash, and KCl. PC3 with moderate loadings of F⁻, PO₄ ³⁻, NO₃ ⁻, and BOD explained with 11.492% of total variance, and F⁻ represents the dissolution of F⁻ bearing minerals. While PC4, PC5, and PC6 explained 9.005, 7.126, and 6.652% of the total variance of data set, respectively. Loadings of the first three components are represented by Fig. 9a.

Fig. 8

a, b Scree plot of the eigenvalues of PCA (May 2013–August 2013)

Table 6 Varimax-rotated factor loadings of groundwater quality parameters

Fig. 9

a, b Rotated loadings for components 1, 2, and 3 (May 2013–August 2013)

PCA of data obtained in August 2013 (pre-monsoon season) extracted six PCs, which accounted for 81.035% of the total variance (Table 6). PC1 explained 32.493% of the total variance and loaded strongly by EC, TDS, TH, Ca²⁺, Mg²⁺, Na⁺, and Cl⁻, moderately by SO₄ ²⁻ and COD, and negatively by pH and temperature (Eigenvalue: 6.800, Fig. 8b). PC2 is loaded primarily by K⁺, F⁻, and BOD which explained 14.905% of the total variance. PC3 is accountable for 11.264% of the total variance and is preeminently represented by F⁻, SO₄ ²⁻, and PO₄ ³⁻. PC4 explained 8.338% of the variance and is best represented by DO and COD, while negatively by temperature and TH. Furthermore, 7.364% of the total variance is explained in PC5 and loaded only by PO₄ ³⁻ and NO₃ ⁻. However, PC6 is responsible for 6.671% of the variance and represented by turbidity. PC1 is represented by Ca²⁺, Mg²⁺, Na⁺, Cl⁻, and SO₄ ²⁻, which demonstrates the concentration of aquifer minerals and secondary evaporation. This factor shows that ionic concentration increases, which lower the pH. These ions gradually increase with TDS; groundwater may be undersaturated among dolomite, calcite, and gypsum, with respect to the solubility product (Zhang et al. 2014). PC2 is represented by K⁺, F⁻, and BOD, which indicates the impact of potassium feldspar and fluorite weathering process. PC3 represented by F⁻, SO₄ ²⁻, and PO₄ ³⁻ implying an effect of the weathering process as well as inputs from agricultural fields. PC4 is not dominated by chemical parameters which implies that this factor is associated with sub-surface activities. PC5 indicates that NO₃ ⁻ and PO₄ ³⁻ are well associated with external activities. NO₃ ⁻ is largely an extensive impurity in groundwater and originates from urban and agricultural activities, but still, the association of PO₄ ³⁻ and NO₃ ⁻ is mainly due to the impact of potash fertilizers in groundwater. Remaining factor is weakly dominated to the total variance of data set explains not much impact on groundwater chemistry. First, three factors are responsible for variation in groundwater. Loadings of the first three components are represented by Fig. 9b.

Cluster analysis

In summer season on May 2013, Q-mode cluster analysis exhibits four most important groups. Group A comprises of 12 samples (Fig. 10a), which all belong from upper to middle of the Amaravathi River basin except, sample 17 and 23, shows a high similarity between the samples in the same geological formation. This group is dominated by both weathering factors. Group B has four members (sample no. 1, 7, 16, and 3), which indicated surface water recharge and water–rock interaction. Group C has two samples (6 and 18) which were highly polluted by different factors, one from the agricultural region (sample no. 6) and sample 18 located near dyeing industry, open sewage, and transport workshop shed. These groups are influenced more by pollution discharge, because the depth of the groundwater is low. Group D consists of 6 samples (sample no. 21, 22, 20, 24, 14, and 19) all are from downstream of the study area; they were highly polluted due to industrial activities, municipal sewage, and runoff from irrigation lands. A similar result is obtained for pre-monsoon season (August 2013) with a little variation among samples in Group A and B of Q-mode hierarchical cluster analysis dendrogram (Fig. 11a).

Fig. 10

a, b Dendrogram of Q and R-mode hierarchical cluster analysis (May 2013)

Fig. 11

a, b Dendrogram of the Q and R-mode hierarchical cluster analysis (August 2013)

Figures 10b and 11b show the dendrogram of R-mode cluster analysis. Based on the figures, three main clusters can be identified among physico-chemical variables. The first cluster consists of EC and TDS, and the second cluster consists of further 17 variables. The second cluster is classified into two more clusters; Cl⁻ makes the first sub-cluster, and Na⁺, HCO₃ ⁻, TH, SO₄ ²⁻, Ca²⁺ in addition to COD, Mg²⁺, K⁺, temperature, DO, pH, F⁻, BOD, NO₃ ⁻, PO₄ ³⁻, and turbidity make the second sub-cluster. The first cluster is affected mainly by salinity factor due to mineral dissolution and second cluster be attributed by multiple factor; there are many processes that influencing the geochemistry of groundwater. Cl⁻ in the first sub-cluster represents flushing of evaporated minerals from sedimentary rocks and half of the second sub-cluster is likely from natural processes, such as strong evaporation, weathering of rich feldspars and mica, whereas the second half of second factor is attributed by anthropogenic sources such as agricultural practices, sewage activities, and wastewater from bleaching industries.

Conclusion

Excess of ions in groundwater makes the water unusable for drinking purposes. Correlation matrices show geogenic process, ion and base exchange, dissolution process, evaporation dominance, agro-chemicals, and anthropogenic activities which enhance the current groundwater chemistry. Principal component analysis extracted 6 PCs which explain 81% of the total variance of the original data matrix and heavily by EC, TDS, TH, Ca²⁺, Mg²⁺, Na⁺, and Cl⁻. The parameters dependable for groundwater quality variations are principally associated with water–rock interaction (natural) and anthropogenic resources. Q-mode CA consists of four main groups, Group D has a high pollution loading comprise of samples 6, 18, and 19. R-mode consists of two clusters; first cluster consists of EC and TDS, and the second cluster consists of all other 17 variables, mainly by Na⁺, HCO₃ ⁻, TH, SO₄ ²⁻, and Ca²⁺ in addition to COD, Mg²⁺, K⁺, temperature, DO, pH, F⁻, BOD, NO₃ ⁻, PO₄ ³⁻, and turbidity. Spatial variation maps show the concentration of physical and chemical parameters covering the study region. These current findings are valuable in prospect actions in river and groundwater management for home government and policy-makers.