Introduction

The textile, leather, paint, cosmetics industries produce large quantities of wastewater containing dyes that are becoming a major environmental concern. It is estimated that 10–15% of dyes are wasted into the environment after their use in dyeing unit (Moussavi and Mahmoudi 2009). In India, an average mill producing 60 × 104 m/day of fabric is likely to discharge approximately 1.5 million L/day of effluent (CPCB 2000). In textile industries, acid dyes are largely used for high solubility, low cost and bright color and they remain unaffected in conventional treatment system (Moussavi and Mahmoudi 2009). The discharge of dye wastewater into the environment is aesthetically displeasing, impedes penetration of light and toxic to environment.

Due to good water solubility and poor biodegradability of acid dyes, it is difficult to eliminate them by conventional aerobic treatment (Robinson et al. 2001). Generation of large volumes of iron sludge and requirement of UV light and formation of byproducts hinder the application of advanced oxidation like Fenton and photo-Fenton process (Ahmad and Kumar 2010). Adsorption is the most versatile and widely used technology for dye removal because of low capital investment, less operating cost and high efficiency. Several low cost adsorbent materials have been developed such as cellulosic orange peel waste, banana pith, rice husk, clay, neem leaf powder, powdered activated sludge, activated carbon, gram husk, coal bottom ash, bagasse fly ash, deoiled soya, red mud, and sawdust (Gupta and Suhas 2009).

However, the major drawback of these materials is nonselective adsorption of acid dyes. Several amine based polymeric compounds were used for the removal of acid dyes. Amine based natural compounds like chitosan and crosslinked chitosan (Saha et al. 2005), ammonium chitosan derivative (Elwakeel et al. 2012) and synthetic polymers like MCM-41, polyaniline (PANI) were used for removals of sulfonated reactive and acid dyes (Qin et al. 2009; Donia et al. 2009; Mahanta et al. 2009; Ahmad and Kumar 2010).

Aniline formaldehyde condensate (AFC) is an amine based polymer, used for the removal of several heavy metals like Cu2+, Cr(VI) in our previous work (Kumar et al. 2007a, b, 2009). AFC is a low cost, short chain polymer with amine group throughout the chain length. To the best of our knowledge, no literature is available on azo dye removal by AFC polymer. Present study was carried out using Acid orange 8 (AO8) and Acid violet 7 (AV7) as model acid azo dyes to study adsorption kinetics, thermodynamics and equilibrium behavior on AFC. Both dyes are used in textile industry (Tunc et al. 2013; Mansour et al. 2007).

Materials and methods

Materials

Commercial grade aniline (C6H5NH2) was purified by distilling over KOH pellets at boiling point temperature of aniline (180 °C). Formaldehyde was purchased from Spectrochem, India and was used as received. Column chromatographic silica gel (60–120 mesh) purchased from Merck was used as received.

AO8 and AV7 dyes were purchased from Sigma-Aldrich, Bangalore and used as received. Both dyes were in powder form and sulfonated monoazo dyes. The chemical formula of AO8 is C17H13N2NaO4S with molecular weight of 364.35 g/mol and C.I. number 1557. AV7 has molecular weight of 566.47 g and formula of C20H16N4Na2O9S2.

Synthesis of polymers

AFC was synthesized by reacting formaldehyde (HCHO) with aniline (C6H5NH2). Detailed procedure is given in previous published literatures (Kumar et al. 2009). In a 100 mL beaker, 10 mL of 37% formaldehyde (123 mmol) was added slowly to a mixture of 18.6 g of aniline (200 mmol) and 6 mL of concentrated HCl and kept in the water bath at 80 °C for 2 h with intermittent stirring. Then it was neutralized with 8 mL of 30% NaOH and kept in the water bath for another 1 h at 60 °C temperature. Thereafter it was removed from the water bath and kept at room temperature for 12 h, then washed for three to four times with warm water to remove residual aniline and formaldehyde and dried by applying vacuum in a vacuum desiccator. AFC synthesized was of yellow color resinous material. In 25 mL methanol (CH3OH) solution, 25–30 g resinous AFC polymer was dissolved at 40–45 °C with stirring. Experimentally, it was observed that maximum 25 g of silica could be added in methanol–AFC solution to completely soak the silica gel and permit mixing. After addition of 25 g silica gel in methanol–AFC mixture, manual stirring was applied for 5 min. Then excess liquid was removed by filtering and AFC coated on silica gel was air dried for 6 h. This AFC coated silica gel was used as the adsorbent for removal of acid dyes.

Adsorption experiment

Initial solution pH, dose of adsorbent, temperature and initial concentration of dye were variable parameters for this study. All experiments were carried out with 250 mL of dye solution in 500 mL plastic bottles. Predetermined quantities of adsorbent were added to the bottles and initial solution pH was adjusted at desired value and mixing was achieved in the horizontal incubator shaker at 150 rpm and 37 °C temperature. In pH study, initial pH of dye solution was adjusted using 0.1/1N HCl/NaOH and known amount of adsorbent was added and kept for 12 h without pH control. Adsorbent dose was varied from 0.5 to 12 g/L in a similar manner. In temperature study, temperature was varied from 10 to 50 °C with a known amount of adsorbent for 12 h. For kinetic study, AO8 and AV7 solution with adsorbent was kept in horizontal shaker in different bottles and after regular time interval, each bottle was withdrawn from the shaker. After the experiment, adsorbent was separated from dye solution using centrifuge at 100 rpm and residual concentration of dye and final pH was estimated. The amount of dye adsorbed on AFC was calculated based on the difference of dye concentrations in aqueous solution before and after adsorption experiment according to Eq. (1):

$$ q_{t} = \frac{{(C_{0} - C_{t} ) \times V}}{m}, $$
(1)

where, q t is the amount of dye adsorbed per unit weight of adsorbent (mg/g) at time t, C 0 and C t are the concentrations of dye (mg/L) at initial time and at time t, respectively, V is the initial volume of dye solution (L) and m is the mass of adsorbent (g). When t is equal to the equilibrium time, C t  = C e, q t  = q e, then the amount of dye adsorbed at equilibrium was calculated using the same Eq. (1). All experiments were done at least two times and average value of residual dye concentration was used in this study.

Desorption study

Desorption study was done using AO8/AV7 loaded AFC with different strengths of NaOH (0.05–0.5N) as desorbing agent. Desorbent volume was 50 mL in each case and desorption experiments were performed in a horizontal shaker at 150 rpm for 6 h. Then the samples were centrifuged and analyzed for dye concentration in desorbent solution. Desorption amount was calculated using Eq. (2):

$$ {\text{Desorption}}\;(\% ) = \frac{{(V_{\text{des}} \times C_{\text{des}} ) \times 100}}{{(C_{0} - C_{\text{e}} )V_{\text{ads}} }}, $$
(2)

where, V des is the volume of desorbent used (50 mL), C des is the final concentration of dye in solution after desorption (mg/L), C e is equilibrium dye concentration after adsorption (mg/L), C 0 is the initial dye concentration before adsorption (mg/L) and V ads is the volume of dye solution used for adsorption experiment (250 mL).

Analytical procedure

Zero point charge of adsorbent was estimated using immersion technique as described by Fiol and Villaescusa (2009). Characterization of AFC was carried out using FTIR (Perkin Elmer, PE-RXI), FESEM (Hitachi 5500 FESEM), Particle size analyzer (Mastersizer 2000, Malvern) and BET surface area analysis (Autosorb-IQ MP).

The maximum wavelength for AO8 and AV7 were observed at 490 and 520 nm, respectively, after scanning in UV–visible spectrophotometer from 400 to 800 nm. Effect of solution pH on absorbance of dye was determined by varying initial pH (1–10) of AO8 solution of concentration 20 mg/L. It was observed that within pH 6–7, maximum absorbance was achieved. All measurements of residual dye were carried out at this solution pH. Calibration curve was prepared by dissolving known amount of dye powder in distilled water and adjusting solution pH to 3 and then absorbance was measured at 490 nm wavelength. AO8 dye followed Beer’s law up to concentration of 25 mg/L. The absorbance values were plotted against these known concentrations and linear absorbance curve was obtained with correlation coefficient of 0.99. In a likely manner, the solution pH for maximum absorbance of AV7 was determined and it showed maximum absorbance at pH of 7–8 and all analysis of AV7 dye were carried out at this pH. AV7 showed linear absorbance up to concentration of 40 mg/L.

Results and discussion

Characterization of the polymers

The particle size analysis of AFC-silica gel was evaluated volume wise for range of particle size. It was observed that mean particle diameter was 353 μm. FESEM image of AFC is shown in Fig. 1. The surface of AFC-silica gel shows that the surface was uneven. The point of zero charge (pHzpc) was determined from the change of pH. It can be seen that pH change was minimum when initial pH was 5.5. The surface area of the adsorbent was determined using standard nitrogen adsorption porosimetric technique employing the BET method. BET specific surface area was 20.850 m2/g. N2 adsorption isotherm on AFC is shown in Fig. 1. According to IUPAC classification, it followed Type-IV isotherm (Sing et al. 1985). Pore volume and pore radius of AFC were determined by employing the BJH method. Pore volume was 0.051 cc/g and pore diameter of 4.91 nm, suggesting mesoporous adsorbent.

Fig. 1
figure 1

Characteristics of AFC polymer a FESEM image; b pH for zero point charge; c BET isotherm

Full size image

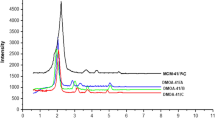
Fourier transform infrared spectrometer (FTIR) spectra of AFC polymer before and after adsorption of AO8 and AV7 are given in Fig. 2. The broad peak at 3400–3500 and 1550 cm−1 were the characteristics peaks for NH2 (Yang and Feng 2010). The peaks at 500 and 1000 cm−1 are due to Si–O–Si asymmetric stretching vibration (Donia et al. 2009). After adsorption of dyes, the band at 3400–3500 and 1550 cm−1 diminished.

Fig. 2
figure 2

FTIR spectra of AFC before and after adsorption of AO8 and AV7 dyes

Full size image

Effect of initial solution pH

The optimum pH for dye uptake was determined and results are shown in Fig. 3. Acidic pH favored removals of both dyes. Maximum uptake was achieved at pH of 3 for AO8 and at pH of 2 for AV7 dye. The uncoated silica gel was used for the removal of AO8 and AV7 dye and it was observed that with 3 g/L dose of silica gel, dye removal was only 7% for AV7 and 8% for AO8 dyes. This indicates that removal of dyes mainly occurred by polymer. Final pH is shown in Fig. 3. Change in pH followed similar trends for both dyes. Increase in pH was observed, when initial pH was less than 6 and decreased when initial pH was higher than 6.

Fig. 3
figure 3

Effect of solution pH on dye uptake and change in pH a AO8 and b AV7

Full size image

Acid dyes are anionic in nature and highly water soluble. They are effective for dyeing protein fibers like wool, nylon and silk (Donia et al. 2009). Acidic acid is used as a stimulator in dyeing process to adjust pH 3–4 (Chiou et al. 2004). Since AFC is more effective to remove acid dyes at lower pH, no pH adjustment will be required for the treatment of acid dye containing industrial wastewater by AFC.

Effect of temperature and thermodynamics

Temperature was varied from 10 to 50 °C using initial dye concentration of 100 mg/L at initial pH of 3. With increase in temperature, uptake of AO8 increased and AV7 decreased (Fig. 4).

Fig. 4
figure 4

a Effect of temperature on dye uptake. b van’t Hoff plot

Full size image

Thermodynamic parameters like enthalpy change (ΔH°) (J/mol) and entropy change (ΔS°) (J/mol K) were evaluated using van’t Hoff equation given below (Liu et al. 2015) and the plot is shown in Fig. 4b:

$$ \ln K_{\text{L}} = \left( { - \frac{\Delta H^\circ }{RT}} \right) + \frac{\Delta S^\circ }{R}, $$
(3)

where, K L is distribution coefficient for adsorption given as \( \frac{{q_{\text{e}} }}{{C_{\text{e}} }} \) L/g); R is universal gas constant (8.314 J/mol K) and T is absolute temperature (K). Free energy change (ΔG°) (J/mol) was calculated using Eq. (4) Liu et al. (2015):

$$ \Delta G^\circ = \Delta H^\circ - T\Delta S^\circ . $$
(4)

Values of thermodynamic parameters are given in Table 1. AO8 removal was endothermic and removal of AV7 was exothermic in nature. Enthalpy change was much higher for AO8 (19.97 kJ/mol) than AV7 (−5.45 kJ/mol). The heat of adsorption less than 20 kJ/mol suggests that AV7 and AO8 adsorption processes were physical in nature. Entropy change was positive for AO8 and negative for AV7. Negative entropy change of AV7 dye indicated decreased disorder at solid-solution interface. Adsorption was spontaneous for AO8 from 10 to 50 °C and for AV7 from 10 to 40 °C.

Table 1 Thermodynamic parameters for AO8 and AV7 dyes on AFC
Full size table

Effect of adsorbent dose

Dosage was varied from 0.5 to 12 g/L using 100 mg/L of AO8 and AV7 dyes at initial pH of 3. Initially with increase in adsorbent dose (0.2–12 g/L), removal of AO8 increased and the increase was substantial when the dose was increased from 0.5 to 2 mg/L (Fig. 5). At adsorbent dose of 3.6 g/L, it achieved a plateau with 99% removal. In case of AV7 dye, removal increased up to a dose of 10 g/L with maximum removal of 75%. The maximum uptakes were 164 mg/g (0.45 mmol/g) for AO8 and 68 mg/g (0.12 mmol/g) for AV7.

Fig. 5
figure 5

Effect of AFC dose on dye uptake

Full size image

Adsorption isotherm

Isotherm plots (q e vs C e) are shown in Fig. 6. Isotherm shapes were convex type for AO8 and concave type for AV7. Based on isotherm classification provided by Giles et al. (1974a), AO8 adsorption on AFC followed L2 type isotherms and AV7 followed S1 type isotherm. Based on another classification of IUPAC (Sing et al. 1985), AO8 isotherm was of Type I and AV7 was of Type III.

Fig. 6
figure 6

Isotherm plots of AO8 and AV7 dyes on AFC

Full size image

Several isotherm models were used to explain the behavior of dyes on AFC polymer. Langmuir, Freundlich and Tempkin models are given respectively in Eqs. (5–7) (Foo and Hameed 2010):

$$ q_{\text{e}} = \frac{{Q_{\text{m}} \;b\;C_{\text{e}} }}{{1 + b\;C_{\text{e}} }}, $$
(5)
$$ q_{\text{e}} = K_{\text{f}} C_{\text{e}}^{1/n} , $$
(6)
$$ q_{\text{e}} = \frac{RT}{\Delta Q}\ln A_{\text{T}} C_{\text{e}} , $$
(7)

where, q e is the amount of dye adsorbed at equilibrium (mg/g); C e is the aqueous phase dye concentration at equilibrium (mg/L); Q m is the adsorption capacity of the adsorbent (mg/g), b is the affinity constant for adsorption (L/mg) in Langmuir model. K f is the Freundlich capacity factor and n is the index of heterogeneity. In Tempkin model (Eq. 7), R is gas constant, T is temperature (K), ΔQ is the variation of adsorption energy (kJ/mol) and A T is Tempkin equilibrium constant (L/mg).

Isotherm parameters were determined using nonlinear regression and experimental isotherm data were compared with modeled data in a plot. The fitness of experimental and model data was verified from correlation coefficient (R 2) and average relative error (ARE) (Eq. 8):

$$ {\text{ARE}} = \frac{100}{n}\mathop \sum \limits_{i = 1}^{n} \left| {\frac{{(q_{\text{eexp}} - q_{\text{ecal}} )}}{{q_{\text{eexp}} }}} \right|i, $$
(8)

where, q eexp and q ecal dye uptake values observed experimentally and calculated using isotherm model, respectively. Isotherm parameters are given in Table 2. In Fig. 6, experimental and modeled isotherm plots are shown for both dyes. For AO8 dye, both Langmuir and Freundlich models provided R 2 value of 0.99 and lowest ARE value was obtained with Langmuir model. Figure 6 also shows that experimental data followed Langmuir model (green line) pretty well. Hinz (2001) suggested that L type isotherm can be described by Langmuir model. It is evident that AO8 adsorption on AFC can be best described by Langmuir model with maximum monolayer uptake of 252 mg/g and affinity constant of 0.054 L/mg.

Table 2 Estimated isotherm parameters for adsorption of AO8 and AV7 dyes on AFC polymer at pH 3 and 37 °C
Full size table

Adsorption isotherm of AV7 dye showed an upward curvature. Langmuir and Tempkin models were unable to fit experimental data with low R 2 value and high ARE value (Table 2). Previous researchers observed that for this type of isotherm, Freundlich, BET models fit experimental data better (Hinz 2001; Girods et al. 2009). BET model is given in Eq. (9):

$$ q_{\text{e}} = \frac{{Q_{\text{m}} B C_{\text{e}} }}{{(C_{\text{s}} - C_{\text{e}} )\left[ {1 + (B - 1)\left( {\frac{{C_{\text{e}} }}{{C_{\text{s}} }}} \right)} \right]}}, $$
(9)

where, Q m is the amount adsorbed in a complete monolayer, B is equilibrium constant and C s is the saturation concentration of adsorbate in water. Figure 6 shows that experimental isotherm data of AV7 dye followed both BET and Freundlich models. However, Table 2 shows that Freundlich model provided higher R 2 and lower ARE value than BET model. Also, BET isotherm provided exceptionally high Q m value, than observed in this study. Since, AV7 adsorption on AFC followed Freundlich isotherm, the adsorption was heterogeneous and multilayer. The slope in Freundlich model, 1/n, was higher than 1, suggesting cooperative adsorption of AV7 adsorption on AFC. Giles et al. (1974b) reported that S type isotherm many times follow cooperative adsorption, where adsorbate molecules tending to be adsorbed in rows or clusters.

Effect of initial dye concentration

Dye uptakes with time at varying initial concentrations (20–150 mg/L) for AO8 and AV7 are given in Fig. 7. At lower adsorbate concentration (20 and 50 mg/L) both dyes had shown comparable uptakes (6 and 5 mg/g at 20 mg/L and 14.6 and 14.2 mg/g at 50 mg/L for AO8 and AV7, respectively). With increase in initial dye concentration, uptakes increased and uptake was much higher for AO8 (46 mg/g) than AV7 (25 mg/g) at initial dye concentration of 150 mg/L. Figure 7 shows that equilibrium time was 180 min for AO8 concentration of 20–50 mg/L and increased to 600 min, at AO8 concentrations of 100 and 150 mg/L. With AV7, equilibrium time was longer, 660–720 min at 20–50 mg/L concentration and increased to 1020 min at concentrations of 100 and 150 mg/L.

Fig. 7
figure 7

Uptake of dyes with time a AO8 and b AV7

Full size image

Adsorption kinetics

Kinetic data of AO8 and AV7 on AFC (Fig. 7) were analyzed using intraparticle diffusion model (Weber and Morris 1963) (Eq. 10):

$$ q_{t} = \, k_{\text{i}} t^{0.5} + y, $$
(10)

where q t (mg/g) is the amount of dye adsorbed on AFC at different times t (min), k i is the rate of intraparticle diffusion (mg/L min0.5) and intercept, y is the thickness of the boundary layer. Intraparticle diffusion becomes the sole rate limiting step in adsorption, when intercept becomes zero. Plots are shown in Fig. 8. It is evident that plots were straight lines but did not pass through origin, suggesting AO8 and AV7 adsorption on AFC involved intraparticle diffusion, but it was not sole rate controlling step.

Fig. 8
figure 8

Intraparticle diffusion plots for AO8 and AV7 dyes on AFC

Full size image

The slope of the plot of the linear part of the q t against t 0.5 plot (here taken between 15 and 200–240 min) gives the values of diffusion rates (k i). Values of diffusion rates (k i) are given in Table 3. Regression analysis showed initial internal adsorption rate with dye concentration followed by the following relation.

$$ k_{\text{i}} = ( - 2.60)C_{0}^{0.012} \,({\text{AO8}}), $$
(11)
$$ k_{\text{i}} = ( - 2.73)C_{0}^{0.008} \,({\text{AV7}}). $$
(12)
Table 3 Kinetic parameters of AO8 and AV7 dyes adsorption by AFC polymer
Full size table

Reichenberg (1953) model was used to understand the role of external mass transfer/film diffusion on adsorption of acid dyes by AFC (Eq. 13):

$$ F = 1 - \frac{6}{{\pi^{2} }} \mathop \sum \limits_{n = 1}^{\infty } \frac{1}{{n^{2} }} \exp \left( {\frac{{ - n^{2} D_{\text{s}} \pi^{2} t}}{{R^{2} }}} \right), $$
(13)

where, F is fractional uptake at any time t (min) and F = \( \frac{{q_{t} }}{{q_{\text{e}} }} \), q t and q e are dye uptakes at time t and equilibrium, respectively, D s is the effective diffusion coefficient (cm2/min), n is an integer that defines the infinite series solution. In Eq. (13), \( \frac{{\pi^{2} D_{\text{s}} }}{{R^{2} }} \) is substituted by B and shown in Eq. (14) (Reichenberg 1953):

$$ F = 1 - \frac{6}{{\pi^{2} }} \mathop \sum \limits_{n = 1}^{\infty } \frac{1}{{n^{2} }} \exp (n^{2} Bt). $$
(14)

The values of Bt for each value of F was calculated as proposed by Reichenberg (1953) and given below:

$$ F{\text{ values}} < 0. 8 5,\quad \,Bt = 6.28318 - 3.2899F - 6.28318(1 - 1.0470F)^{{\frac{1}{2}}} , $$
(15)
$$ F{\text{ values}} > 0. 8 5,\quad Bt = - 0.4997 - \ln (1 - F). $$
(16)

The plots of Bt vs. t (Boyd’s plot) are shown in Fig. 9 for both dyes. The plots were nonlinear and did not pass through origin for both AO8 and AV7, suggesting that during initial 90–120 min, external resistance was strong and external mass transfer was controlling step in adsorption, though diffusion was also important in AO8 and AV7 adsorptions. Mohan and Singh (2002) cited that low concentration of adsorbate, inadequate mixing, high affinity between adsorbate and adsorbent as reasons for film diffusion to be controlling step in adsorption. The lower initial dye concentration was probably responsible for adsorption controlled by external mass transfer/film diffusion.

Fig. 9
figure 9

Boyd’s plots for AO8 and AV7 dyes on AFC

Full size image

Desorption and reuse

Desorption of dyes from AFC surface was studied using varying strength of NaOH solution (0.0.5–0.5N). Maximum desorption was achieved at NaOH strength of 0.1N for AO8 and AV7. However, desorption of AV7 was much higher (88%) than AO8 (49%) as shown in Fig. 10.

Fig. 10
figure 10

Desorption of dyes from AFC

Full size image

Cost analysis of AFC coated silica gel with chitosan

In a single batch of AFC synthesis, yield of AFC-silica is 30–33 g and total cost of AFC-silica (based on raw materials) is Rs. 169/30 g, with Rs. 5.63/g. Price of chitosan varies in a wide-range from Rs. 700–1390/25 g with Rs. 28–55/g. Cost of chitosan as an adsorbent is many folds higher than AFC-silica, which may be useful for the treatment of large volume of dye containing wastewater at a lower cost.

Dye removal capacity of AFC-silica was compared with published results using an acid dye, Methyl orange (MO) and results are given in Table 4. It can be seen that Zr(IV) immobilized chitosan/bentonite composite had four times higher uptake of MO dye than AFC-silica. Another Chitosan/alumina composite showed twofold higher uptake of MO dye than AFC-silica in similar experimental condition. Cost analysis showed simple chitosan was higher than AFC-silica by more than fivefold, suggesting applicability of AFC-silica.

Table 4 Comparison of AFC-silica with chitosan based adsorbents for adsorption of methyl orange (MO) dye
Full size table

Dye removal mechanism by AFC polymer

In the aqueous solution, the sulfonate groups of the acid dyes (R-SO3Na) were dissociated and converted to anionic dye ions (R-SO3 −). At lower pH, many hydrogen ions were available in solution and amine group (–NH2) of AFC accepted protons and remained in protonated form (NH3 +) and solution pH increased. Electrostatic attraction between amine (NH3 +) and anionic dye molecule (R-SO3 −) was responsible for higher uptakes of AV7 and AO8 at strong acidic pH (2–3). At neutral and alkaline pH, AFC surface was in deprotonated form (–NH2) and electrostatic attraction and dye uptake decreased. Similar mechanism for acid dye uptake by amine group of chitosan and crosslinked chitosan were suggested by previous researchers (Liu et al. 2015; Elwakeel et al. 2016a, b). pHzpc of AFC was observed as 5.5, suggesting that above this pH value, AFC surface had negative charge and Fig. 3 shows that some adsorption of dyes still occurred within pH range of 5.5–10. Electrostatic attraction could not be responsible for dye removals above pH 5.5. Hydrogen bond formation between nitrogen of amine group of polymers and OH group of dye, hydrophobic interaction between aromatic group of dye and polymers are other possible mechanisms of AO8 and AV7 removal from solution. Dye removal mechanism by AFC is shown in Fig. 11.

Fig. 11
figure 11

Dye removal mechanism by AFC

Full size image

Maximum dye uptakes were different for both the dyes, with AO8 maximum uptake was 164 mg/g (0.45 mol/g) and AV7 maximum uptake observed was 68 mg/g (0.12 mmol/g). Structure of dye was responsible for difference in uptake. AO8 dye was monovalent with single SO3 − group and AV7 dye was divalent (two SO3 −) (Fig. 10). AO8 was smaller than AV7 in molecular size and this helped in higher diffusion of AO8 dye molecules. Higher diffusion rates (k i) in Table 3 also confirm this. Further, when same adsorbent dose and same initial dye concentration was used, dye:AFC ratio was higher for AO8 than AV7. At AFC dose of 1 g/L and initial dye concentration of 100 mg/L, AO8:AFC ratio was 0.27 mmol/g and AV7:AFC ratio was 0.17 mmol/g. Higher dye: AFC ratio, increased chances of interaction between adsorbate and adsorbent molecules and enhanced dye uptake. A similar phenomenon was observed during adsorption of acid dyes on chitosan (Wong et al. 2003).

Conclusion

Adsorption kinetics, thermodynamics and equilibrium behavior of two acid azo dyes (Acid orange 8 and Acid violet 7) on amine based polymer, named aniline formaldehyde condensate (AFC) were studied. Adsorption of both dyes was favored in acidic pH. Electrostatic attraction with protonated amine group of AFC and hydrophobic–hydrophobic interaction and hydrogen bonding were responsible for dye uptake. AO8 adsorption isotherm was of Type I and followed Langmuir model. Adsorption isotherm of AV7 was of Type III and it followed Freundlich model. External mass transfer controlled dye adsorption on AFC. Maximum adsorption capacities of AO8 and AV7 were observed as 164 and 68 mg/g, respectively. Higher molecular weight of divalent AV7 dye was responsible for lower dye: AFC ratio in solution, resulting lower uptake of AV7.