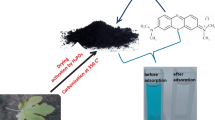
Abstract
This study investigates the potential of the stem axis of Artocarpus odoratissimus fruit (TSA) as an adsorbent for the removal of methyl violet 2B (MV). The functional group analysis was carried out using Fourier-transform infrared spectroscopy. Investigation of the effects of pH and ionic strength provide insights on the involvement of electrostatic attraction and hydrophobic–hydrophobic attraction between the adsorbent and adsorbates. Kinetics models (pseudo-first-order, pseudo-second-order, Weber–Morris and Boyd) and isotherm models (Langmuir, Freundlich and Dubinin–Raduskevich) were used for characterising the adsorption process. The Langmuir model predicted a high q m of 263.7 mg g−1. Thermodynamics studies indicate the adsorption system is spontaneous, endothermic and physical sorption dominant. The spent adsorbent was successfully regenerated using water and obtained adsorption capacity close to the unused adsorbent even after fifth cycle of washing.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Textile industry is a very high water intensive and a mill of production rate of 8000 kg per day of fabric utilise 1.6 million litres of freshwater with the dyeing section producing up to 15% of total wastes (Kant 2012). Synthetic dye itself is usually designed to withstand heat, photo or chemical degradation. The dye wastewater if not disposed properly can lead to severe ecological destruction, especially if discharged directly into the river which is still common practice in some low income countries (Ahmed et al. 2012; Awomeso et al. 2010; Mittal 2016). Damages may not be limited to aquatic life forms, but may spread downstream to agricultural land, aquaculture farms or bring harm to whoever utilise the water resources.
A few common industrial wastewater remediation methods include ozonation, membrane filtration, adsorption (Kooh et al. 2016b), ion-exchange (Naushad et al. 2015) and phytoremediation (Kooh et al. 2016c). Adsorption is the most popular water remediation method (Wang et al. 2011) due to its simple remediation process and can be adopted by any textile mill without the need of advanced knowledge. The cost of the water treatment depends on the type of adsorbent and its adsorption efficiency. Examples of low-cost alternatives may include soil materials such as peat (Chieng et al. 2015), abundant weeds (Lim et al. 2016), or wastes derived from agriculture or industries such as walnut shell (Dahri et al. 2014), breadfruit peel (Lim et al. 2014b), soya waste (Kooh et al. 2015a; Mital and Kurup 2006), dextrin (Mittal et al. 2016b), alginate (Mittal et al. 2016a, c), egg shell (Mittal et al. 2016e), hibiscus fibre (Sharma et al. 2015) and hen feather (Mittal and Mittal 2015). However, the adsorption capacity of absorbents varied with the type of dyes. Carbonaceous materials such as carbon nanotube (Mittal et al. 2016d) and activated carbon may be effective for multiple types of dyes, however, treatment may be expensive. Moreover, activated carbon may have higher carbon footprint due to high amount of energy and chemical required to produce it (Al-Degs et al. 2008).
This research aimed to investigate the usefulness of tarap stem axis (TSA) as a potential adsorbent for the removal of methyl violet 2B (MV). Tarap (Artocarpus odoratissimus) is an evergreen tree belonging to the family Moraceae, native in the Borneo island and have been cultivated in the Philippines, Thailand and as far as the state of Florida in North America. The tarap fruit is formed from multiple flowers held by a stem axis. Each flower has an ovary which develops into small fruits and clustered or fused together into a larger fruit known as collective fruit or multiple fruit. The edible portion of tarap composed of only the white fleshy pulp (24–33%), while the non-edible portion consist of fruit rind (approximately 50%), and a huge stem axis (17–26%) (Tang et al. 2013). The TSA is slightly spongy, can be easily processed into fine powder, and is unexplored as an adsorbent for textile waste. The only report regarding TSA is the use as an adsorbent for removal of Cd (II) and Cu (II) (Lim et al. 2012). There are some reports of dye wastewater remediation using tarap skin in the removal of methylene blue, methyl violet 2B (MV) and crystal violet (Kooh et al. 2015a; Lim et al. 2015).
This study focuses on the dye MV because of its importance as a purple dye in textile industry. Other industrial applications include paper printing, inks, toners, leather, rubber, adhesives and petroleum products (Sabnis 2010). MV used for textile purposes is very cheap and can be purchased for as low as US$ 5/kg of powder. MV is often confused with another important purple dye, crystal violet (methyl violet 10B), in which they differed very much in applications. MV is a known irritant to eyes, skin, gastrointestinal and respiratory tract. Animal testing reported high toxicity to fish with a LC50 at level of 0.047 mg L−1 for Pimephales promelas (fathead minnow) (Sigma-aldrich 2012). It is also known to possess carcinogenic (Vachalkova et al. 1995) and mutagenic properties (Michaels and Lewis 1985).
The objectives of this study include the functional group analysis of the adsorbent, investigation of the effects of adsorbent dosage, pH, initial dye concentration and contact time. Isotherm and kinetics models were included to characterise the adsorption process. Thermodynamics and regeneration experiments were also carried out.
Material and method
Preparation of adsorbent and adsorbate
Tarap fruits were obtained from local market. The tarap rind and the fleshy pulps were removed from the TSA. TSA was washed with distilled water, diced into small pieces and dried in an oven at 85 °C. Dried TSA was blended into fine powder using a kitchen blender and sieved to size of less than 355 μm and stored in a desiccator.
Methyl violet 2B dye (MV) (C24H28N3Cl; Mr 393.95 g mol−1, 80% dye content) was obtained from Sigma-Aldrich. Desired amount of MV powder was dissolved in distilled water to prepare 1000 mg L−1 stock solution. Serial dilution of stock solution was carried out to obtain lower concentrations of MV.
Characterisations of adsorbent
Fourier transform infrared (FTIR) spectra were carried out using the KBr disc approach to determine the functional groups present in the adsorbent, before and after treatment of dye. KBr (Sigma-Aldrich, spectroscopy grade) was dried at 110 °C in an oven for 3 h before using. All FTIR spectra was obtained using a Shimadzu Model IRPrestige-21 spectrophotometer.
The point of zero charge (pHpzc) of the adsorbent was determined by the salt addition method using 0.1 mol L−1 KNO3 solutions (Zehra et al. 2015). Briefly, the pH of the KNO3 solution (20.0 mL) was adjusted with dilute solution of HNO3 and NaOH to obtained initial pH ranged from 2.0 to 10.0. Adsorbent (0.04 g) was added, sealed with parafilm, agitated for 24 h at 250 rpm using a Stuart orbital shaker and the final pH was measured. The pH difference, ∆pH (final pH–initial pH) vs initial pH was plotted to determine the pHpzc.
Batch adsorption procedures
The batch adsorption experiments were carried out by mixing TSA (0.04 g) with MV (20 mL) in clean Erlenmeyer flasks and agitated at 250 rpm. The concentration of the dye was determined using a Shimadzu UV-1601PC UV–visible spectrophotometer at wavelength 584 nm.
Investigation of the effects of dosage (0.01–0.06 g), pH (2–10), ionic strength (0–0.8 mol L−1 NaCl), initial dye concentration (20–500 mg L−1) and contact time (5–240 min) were conducted by changing one parameter at a time, while other parameters being kept constant.
The amount of MV adsorbed per gram of adsorbent at equilibrium, q e (mg g−1), and the removal efficiency are calculated using the following equations:
where C i is the initial dye concentration (mg L−1), C e is the dye concentration at equilibrium (mg L−1), V is the volume of dye used (L) and m is the mass of TSA (g).
To characterise the adsorption process, three isotherm models [Langmuir (1916), Freundlich (1906) and Dubinin–Radushkevich (D–R) (1947)] were used. The kinetics data was modelled with four kinetics models [pseudo-first-order (Lagergren 1898), pseudo-second-order (Ho and McKay 1999), Weber–Morris intraparticle diffusion (1963a) and Boyd (1947) models].
Thermodynamics study
The Van’t Hoff equation is used to model the thermodynamics experiment (at temperature 25–65 °C) and the equation is expressed as:
where ∆G o is the Gibbs free energy, ∆H o is the change in enthalpy, ∆S o is the change in entropy and T is the temperature (K), k is the distribution coefficient for adsorption, C s is the concentration of dye adsorbed by the adsorbent at equilibrium (mg L−1), C e is the concentration of dye remains in solution at equilibrium (mg L−1), and R is the gas constant (J mol−1 K−1).
By substituting Eq. (3) into Eq. (4) resulted in the equation as follows:
The thermodynamics parameters were obtained from the linear plot of ln k vs T −1.
Regeneration experiment
The regeneration experiment were investigated using three solvents (distilled water, 0.1 mol L−1 HNO3 and 0.1 mol L−1 NaOH), and the detailed procedure was described in our previous work (Dahri et al. 2014). Dye-treated adsorbent was prepared using 100 mg L−1 MV and was washed thoroughly using distilled water. The regenerated adsorbent was collected and dried at 70 °C for 24 h. The acidic and basic washing was carried out by agitating the dye-treated adsorbents in respective solvents for 30 min, followed by repeated distilled water washing until the pH of the washed solution is close to neutral. All the spent adsorbent was regenerated up to five cycles.
Results and discussion
Functional group analysis
The FTIR spectra provide valuable insight on the types of functional groups exist on the adsorbent’s surface and also to check the loading of dye onto the adsorbent. According to the FTIR spectrum, untreated TSA contains broad adsorption band at 3384 cm−1 which due to the vibration of –OH and –NH functional groups, C–H band (2919 cm−1), C=O bending (1611 cm−1) and C–O–C stretching band (1058 cm−1). FTIR spectrum for MV-treated TSA displayed shifts of bands for –OH or –NH (3395 cm−1), C=O (1587 cm−1) and C–O–C (1055 cm−1) indicating these functional groups may be interacting with the MV dyes. There are new bands formed only in the FTIR spectra of MV-treated TSA. The new band at 1172 cm−1 represents the C–N stretching vibration of MV and confirms the loading of MV. Another new band at 1367 cm−1 is due to the –COO− anti-symmetric stretching which indicate this functional group may also be interacting with the dye. These observations were also reported in the adsorption of MV using Azolla pinnata (Kooh et al. 2015b).
Effect of dosage
Adsorbent dosage is an important parameter in adsorption system and optimum dosage needs to be determined prior to the start of any experiment. The effect of adsorbent dosage is summarised in Fig. 1a. Adsorption system for MV was observed to have gradual increase in dye removal from dosage of 0.01–0.04 g, while beyond 0.04 g resulted in a small increase in the removal of dyes. The optimum adsorbent dosage was determined to be 0.04 g with removal efficiency of 87.2%. The initial increase is most likely due to more adsorption sites available as dosage increase. Little improvement beyond dosage of 0.04 g could be due to the higher collision rate between the adsorbent particles leading to overlapping and aggregation thus limiting the availability of adsorption sites for dye interaction.
Effects of pH and ionic strength
The adsorption of dye usually occurs by three main mechanisms: electrostatic attraction, hydrophobic–hydrophobic interactions and hydrogen bonding. Electrostatic attraction is defined as attraction between the charged groups between the dye molecule and the adsorbent, while hydrophobic–hydrophobic interaction occurs between non-polar groups (Hu et al. 2013). Electrostatic attraction is directly controlled by the pH of aqueous solution. The pH and ionic strength of solution are important parameters to include in the studies. Different solution pHs lead to different net charge on the adsorbent’s surface. To investigate the effect of pH on adsorption process, one of the most common method is the determination of the point of zero charge (pHpzc) of the adsorbent, which is the pH at which the net surface charge is zero. In this study, the pHpzc of TSA was determined to be at pH 4.34. When solution pH is higher than pH 4.34, adsorbent’s surface will become predominantly negative charged, while the opposite applies when solution pH is lower than pH 4.34.
The effect of pH on the adsorbent of MV using TSA is summarised in Fig. 1b. Removal efficiency of 74.8% was observed at pH 2, while pH at 4.2 resulted in higher removal at 87.2%. pH higher than 4.2 did not significantly increase the removal efficiency. This behaviour can be explained with the concept of pHpzc where pH >4.0 resulted in more negatively charged adsorption sites available for attraction of the cationic MV molecules. The reason that the removal efficiency at pH < pHpzc is not zero is because this adsorption system is not purely by electrostatic attraction.
The effect of ionic strength is summarised in Fig. 1c. Salt concentration is directly proportional to the ionic strength. It can be observed that the increase of NaCl concentration lead to reduction in the removal efficiency. At 0.8 mol L−1 NaCl, removal efficiency was reduced from 87.8 to 71.3%. The decrease in removal efficiency is due to the suppression of electrostatic interaction due to competition of Na+ with the cationic MV dye molecules for adsorption sites, where when in excess the Na+ ions occupied the adsorption sites causing electrostatic repulsion of cationic MV molecules (Hu et al. 2013; Vilar et al. 2005). High removal efficiency of 71.3% after suppression of electrostatic attraction indicates that hydrophobic–hydrophobic attraction could be the dominant force of attraction in TSA-MV adsorption system. This behaviour was also observed in the removal of reactive dye with activated carbon (Al-Degs et al. 2008). High removal despite high salt concentration indicates the practicability of TSA in real-life situation as dye wastewater is usually high in salt and surfactants.
Effect of initial dye concentration and isotherm modelling
The effect of initial dye concentration (C i) is summarised in Fig. 2. It can be observed that the adsorption of MV increase as the C i increase, e.g. the q e value at 20 mg L−1 MV was 9 mg g−1 and increased to 190 mg g−1 at 500 mg L−1. This behaviour is explained with Fick’s diffusion law where the concentration gradient as the driving force for the mass transfer rate, hence higher C i resulted in higher q e (Frijlink et al. 2015).
This study involves three isotherm models: Langmuir (1916), Freundlich (1906) and Dubinin–Radushkevich (D–R) (1947) for describing the adsorption data.
The Langmuir isotherm is the most common isotherm model. It is based on the assumption of the formation of monolayer coverage of adsorbate onto the adsorbent’s surface which has limited adsorption sites. All sites are the same and have the same energy and the strength of intermolecular attractive forces diminishes with distance. The equation is expressed as follow:
where q m is the maximum monolayer adsorption capacity of the adsorbent (mg g−1), and k L is the Langmuir adsorption constant (L mg−1) which is related to the free energy of adsorption.
The separation factor (R L) is a dimensionless constant and its value indicates if the model is unfavourable (R L > 1), linear (R L = 1), favourable (0 < R L < 1), or irreversible (R L = 0). The equation of R L is expressed as:
where C o (mg L−1) is the initial dye concentration (C o = 500 mg L−1).
The Freundlich isotherm model is also widely applied in adsorption studies. This model assumes multilayer coverage of adsorbates onto the adsorbent’s heterogeneous surface with non-uniform distribution of heat and affinities. The equation is as follows:
where k F (mg1−1/n L1/n g−1) is the adsorption capacity of the adsorbent and n F (Freundlich constant) indicates the favourability of the adsorption process. The adsorption process is considered favourable if 1 < n F < 10.
D–R isotherm is a temperature-dependent model which is usually applied to express adsorption mechanism with a Gaussian energy distribution onto a heterogenous surface. The equation is as followed:
where q m is the saturation capacity (mg g−1), k DR is a D–R constant (mol2 kJ−2), and ε is the D–R isotherm constant which is also known as the Polanyi potential, R is the gas constant (8.314 × 10−3 kJ mol−1 K−1) and T is temperature (K).
The mean free energy, E (kJ mol−1), obtained using D–R constant can be used to distinguish the physical and chemical adsorption. The equation is expressed as:
The parameters of the Langmuir, Freundlich and D-R isotherm models were calculated from the linear plot of: C e/q e vs. C e, ln q e vs. ln C e, and ln q e vs. ε 2, respectively.
The coefficient of determination (R 2) of the isotherm linear plots is one of the tool to determine the best-fitting relationship. To further verify the consistency of an isotherm model, another tool Chi-squared (χ 2) error function was added.
The equation of χ 2 is as followed:
where q e, exp is the experimental data while q e, cal is the calculated data generated from the isotherm model, n is the number of data points in the experiment and p is the number of parameters of the model. Smaller values χ 2 indicate smaller error.
The parameters of the isotherm models are summarised in Table 1. For TSA-MV adsorption system, both the Langmuir and Freundlich models have the highest R 2 value while D–R model has a poor fit. The value of the error function for the Langmuir is the lowest (χ 2 = 4), followed by Freundlich (χ 2 = 24), while D-R model has high error (χ 2 = 726). Thus, in the account of R 2 and χ 2, it is concluded that the Langmuir model best fitted the experimental data. This suggests that the adsorption onto TSA’s surface may result in a monolayer of adsorbates. The q m value for the adsorption of MV onto TSA was determined as 263.7 mg g−1, which is higher than many unmodified adsorbents such as jackfruit rind (126.7 mg g−1) (Dahri et al. 2016), tarap rind (137.3 mg g−1) (Lim et al. 2015) and Casuarina equisetifolia needle (165.0 mg g−1) (Dahri et al. 2013), soya bean waste (180.7 mg g−1) (Kooh et al. 2016a), Azolla pinnata (194.2 mg g−1) (Kooh et al. 2015b) and cempedak-durian peel (238.7 mg g−1) (Dahri et al. 2015), however, lower than water lettuce (267.6 mg g−1) (Lim et al. 2016) and duckweed (332.5 mg g−1) (Lim et al. 2014a).
Effect of contact time and kinetics modelling
As seen in Fig. 3a, adsorption of MV onto TSA was carried out at three different C i. The adsorption process is very rapid at the beginning due to the availability of adsorption sites, followed by much slower adsorption until attaining saturation at 120 min.
Kinetics studies provide insights on the mechanisms of adsorption process. The kinetics data were fitted into four kinetics models: pseudo-first-order (PFO) (Lagergren 1898), pseudo-second-order (PSO) (Ho and McKay 1999), Weber-Morris intraparticle diffusion (WMID) (Weber and Morris 1963a) and Boyd (Boyd et al. 1947) models.
The PFO equation is expressed as:
where q t is the amount of adsorbate adsorbed at time t (mg g−1), k 1 is the PFO rate constant (min−1) and t is the time shaken (min).
The parameters of PFO are obtained from the linear plot of (log q e– q t) vs.t,. The PFO provides an approximate solution to the true first-order rate mechanism. It differs from a true order in two ways. The parameters q e does not represent the number of available sites, and the parameter log q e is often unequal to the intercept of the plot (log q e –q t) vs.t (Aharoni and Sparks 1991).
The PSO equation is expressed as:
where k 2 is PSO rate constant (g mg−1 min−1).
The parameters of PSO are obtained from the linear plot of t/q t vs t. The model is based on the availability of adsorption sites on solid phase, rather than adsorbate concentration in bulk solution. The main advantage of this model is the ability to predict over the whole range of studies in comparison to many kinetics models. If PSO model is applicable, it indicates the electrostatic interaction and chemisorptions mechanism is the rate-controlling step where electron sharing and exchange between the adsorbate and adsorbent are involved (Dileepa Chathuranga et al. 2013; Li et al. 2014).
According to Table 2, the R 2 of PSO are close to 1.0 which displayed strong linearity, while PFO displayed poor fitting of data at all concentrations of MV. The comparison of the predicted q e (q e, cal) with experimental q e (q e, exp) for PSO are very close while the opposite by PFO. Therefore, it is concluded that PSO is the best fit for the adsorption process, and hence electrostatic interaction and chemisorption mechanism may be the rate-controlling step.
The WMID and Boyd models are used to describe the diffusion mechanism as PFO and PSO are not applicable.
The WMID equation is expressed as:
where k 3 is the intraparticle diffusion rate constant (mg g−1 min−1/2) and C is the intercept.
The Boyd model is expressed as:
where F is equivalent to \( \frac{{q_{\text{t}} }}{{q_{\text{e}} }} \) and B t is mathematical function of F.
The parameters of WMID and Boyd models were obtained from the linear plots of q t vs t ½ and B t vs t, respectively.
Intraparticle diffusion mechanism is involved and considered as the rate-limiting step in the adsorption process when the linear plot passes through the origin (Weber and Morris 1963b). The WMID plot as shown in Fig. 3b can be divided into two regions. The fast rapid external diffusion is completed within the first 5 min, and was not observed in the graph. This first region is attributed to intraparticle diffusion, while the second region is attributed to slow equilibrium. The parameter of WMID is summarised in Table 2. The WMID linear plot did not pass through the origin which indicates that the intraparticle diffusion is involved but is not the rate-limiting step. The value of C represents the boundary layer thickness whereby the larger the value, the greater is the boundary layer effect.
In the Boyd model, adsorption can occur within the pores (particle diffusion) or occur at the external surface (film diffusion) (Tavlieva et al. 2013). According to this model, the plot of B t against t (Figure not shown) will yield a straight line passing through the origin if the adsorption is governed by particle diffusion and if not, the process is controlled by film diffusion. From Table 2, the intercept of the Boyd’s plot does not pass through the origin which indicates that the adsorption might be controlled by film diffusion.
Effect of temperature and thermodynamics studies
The investigation of effect of temperature provides insight on the thermodynamics nature of the TSA-MV adsorption system. Increase of temperature from 25 to 65 °C increased the adsorption capacity from 86.7 to 93.6 mg L−1. The increase of adsorption capacity with increasing temperature indicates the TSA-MV adsorption system is endothermic. This is further verified by the positive values of the ∆H° (5.02 kJ mol−1). Value of ∆H°84 kJ mol−1 also indicates that TSA-MV adsorption system is a physical sorption dominant process (Ahmad and Kumar 2010). The ∆G° obtained at temperature of 25, 35, 45, 55 and 65 °C are −4.20, −4.70, −5.04, −5.20 and −5.54 kJ mol−1, respectively. The negative values of the ∆G° indicate the spontaneity nature of these adsorption systems. The positive value of the ∆S° (0.0311 kJ mol−1 K−1) indicated the increase in randomness of the adsorption process, which showed that the adsorption system is favourable.
Regeneration experiment
The proper way of disposing spent adsorbent which contains hazardous dyes is incineration with combustible solvents (Sigma-aldrich 2012). However, this approach may lead to production of toxic gas, increase the carbon footprint and the fuel itself increase the cost of total treatment. Regeneration experiment seek to obtain information on whether the hazardous dye can be desorb with minimal solvent and bypass the conventional incineration process. The ability to reuse and regenerate spent adsorbent is seen as value added to this adsorbent, as not all adsorbents can be regenerated and reused.
The data of the regeneration experiment is summarised in Fig. 4. All three solvents (distilled water, HNO3 and NaOH) were able to regenerate the TSA and retain adsorption capacity close to the unused adsorbent (44.5 mg g−1), where at the fifth cycle the adsorption capacities were 40.3, 43.2 and 45.2 mg g−1, respectively. The regeneration capacity of TSA is compared with another absorbent A. pinnata (AP) in the removal of MV where at the fifth cycle, the adsorption capacities of AP dropped by approximately 45% for distilled water and acid washing (Kooh et al. 2015b). This behaviour could be due to the strength of attraction between the adsorbent’s surface and the dye molecule, where there are more dye molecules bound to the TSA surface by physical adsorption (Van der Waal, electrostatic interaction, hydrophobic–hydrophobic interaction) as compared to AP.
The reason for the NaOH washing to slightly improve the adsorption capacity may be due to the removal of fat, lipid or small molecular lignocellulosic materials that expose more active functional group capable of interacting with the dye molecules. Similar observation was reported in the removal of MV using AP (Kooh et al. 2015b).
Conclusions
This study concluded that TSA is applied successfully as a good adsorbent for removal of MV. The investigation of the effects of pH and ionic strength provide evidence of the involvement of electrostatic attraction and hydrophobic–hydrophobic attraction. Equilibrium of the adsorption process was attained at short duration of time, and the fitting of the Langmuir model predicted a high q m of 263.7 mg g−1. Thermodynamics studies indicate the adsorption system is spontaneous, endothermic and physical sorption dominant. The spent adsorbent was successfully regenerated using water and obtained adsorption capacity close to the unused adsorbent after fifth cycle of washing.
References
Aharoni C, Sparks DL (1991) Kinetics of soil chemical reactions—a theoretical treatment. In: Sparks DL, Suarez DL (eds) Rates of soil chemical processes. Soil Science Society of America, Madison, pp 1–18
Ahmad R, Kumar R (2010) Adsorptive removal of congo red dye from aqueous solution using bael shell carbon. Appl Surf Sci 257:1628–1633
Ahmed TF, Sushil M, Krishna M (2012) Impact of dye industrial effluent on physicochemical characteristics of Kshipra River, Ujjain City, India. Int Res J Environ Sci 1:41–45
Al-Degs YS, El-Barghouthi MI, El-Sheikh AH, Walker GM (2008) Effect of solution pH, ionic strength, and temperature on adsorption behavior of reactive dyes on activated carbon. Dye Pigm 77:16–23
Awomeso JA, Taiwo AM, Gbadebo AM, Adenowo JA (2010) Studies on the pollution of water body by textile industry effluents in Lagos, Nigeria. J Appl Sci Environ Sanit 5:353–359
Boyd GE, Adamson AW Jr, Myers LSM (1947) The exchange adsorption of ions from aqueous solutions by organic zeolites. II. Kinetics. J Am Chem Soc 69:2836–2848
Chieng HI, Lim LBL, Priyantha N (2015) Sorption characteristics of peat from Brunei Darussalam for the removal of rhodamine B dye from aqueous solution: adsorption isotherms, thermodynamics, kinetics and regeneration studies. Desalin Water Treat 55:664–677
Dahri MK, Kooh MRR, Lim LBL (2013) Removal of methyl violet 2B from aqueous solution using Casuarina equisetifolia needle. ISRN Environ Chem 2013:1–8
Dahri MK, Kooh MRR, Lim LBL (2014) Water remediation using low cost adsorbent walnut shell for removal of malachite green: equilibrium, kinetics, thermodynamic and regeneration studies. J Environ Chem Eng 2:1434–1444
Dahri MK, Lim LBL, Mei CC (2015) Cempedak durian (Artocarpus sp.) peel as a biosorbent for the removal of toxic methyl violet 2B from aqueous solution. Korean Chem Eng Res 53:576–583
Dahri MK, Kooh MRR, Lim LBL (2016) Adsorption of toxic methyl violet 2B dye from aqueous solution using Artocarpus heterophyllus (Jackfruit) seed as an adsorbent. Am Chem Sci J 15:1–12
Dileepa Chathuranga PK, Priyantha N, Iqbal S, Mohomed Iqbal MC (2013) Biosorption of Cr(III) and Cr(VI) species from aqueous solution by Cabomba caroliniana: kinetic and equilibrium study. Environ Earth Sci 70:661–671
Dubinin MM, Radushkevich LV (1947) Equation of the characteristic curve of activated charcoal. Proc Acad Sci 55:327
Freundlich HMF (1906) Over the adsorption in solution. J Phys Chem 57:385–471
Frijlink E, Touw D, Woerdenbag H (2015) Biopharmaceutics. In: Bouwman-Boer Y, Fenton-May VI, Le Brun P (eds) Practical pharmaceutics: an international guideline for the preparation, care and use of medicinal products. Springer International Publishing, Cham, pp 323–346
Ho YS, McKay G (1999) Pseudo-second order model for sorption processes. Process Biochem 34:451–465
Hu Y, Guo T, Ye X, Li Q, Guo M, Liu H, Wu Z (2013) Dye adsorption by resins: effect of ionic strength on hydrophobic and electrostatic interactions. Chem Eng J 228:392–397
Kant R (2012) Textile dyeing industry an environmental hazard. Nat Sci 4:22–26
Kooh MRR, Dahri MK, Lim LBL, Lim LH (2015a) Batch adsorption studies on the removal of acid blue 25 from aqueous solution using Azolla pinnata and soya bean waste. Arabian J Sci Eng. doi:10.1007/s13369-015-1877-5
Kooh MRR, Lim LBL, Dahri MK, Lim LH, Sarath Bandara JMR (2015b) Azolla pinnata: an efficient low cost material for removal of methyl violet 2B by using adsorption method. Waste Biomass Valor 6:547–559
Kooh MRR, Dahri MK, Lim LBL, Lim LH, Malik OA (2016a) Batch adsorption studies of the removal of methyl violet 2B by soya bean waste: isotherm, kinetics and artificial neural network modelling. Environ Earth Sci 75:1–14
Kooh MRR, Lim LBL, Lim LH, Bandara JMRS (2016b) Batch adsorption studies on the removal of malachite green from water by chemically modified Azolla pinnata. Desalin Water Treat 57:14632–14646
Kooh MRR, Lim LBL, Lim LH, Dahri MK (2016c) Phytoremediation capability of Azolla pinnata for the removal of malachite green from aqueous solution. J Environ Biotechnol Res 5:10–17
Lagergren S (1898) Zur Theorie der Sogenannten Adsorption gel Ster Stoffe. K Sven Vetenskapsakad Handl 24:1–39
Langmuir I (1916) The constitution and fundamental properties of solids and liquids. J Am Chem Soc 38:2221–2295
Li G, Zhang D, Li Q, Chen G (2014) Effects of pH on isotherm modeling and cation competition for Cd(II) and Cu(II) biosorption on Myriophyllum spicatum from aqueous solutions. Environ Earth Sci 72:4237–4247
Lim LBL, Priyantha N, Tennakoon DTB, Dahri MK (2012) Biosorption of cadmium(II) and copper(II) ions from aqueous solution by core of Artocarpus odoratissimus. Environ Sci Pollut Res Int 19:3250–3256
Lim LBL, Priyantha N, Chan CM, Matassan D, Chieng HI, Kooh MRR (2014a) Adsorption behavior of methyl violet 2B using duckweed: equilibrium and kinetics studies. Arab J Sci Eng 39:6757–6765
Lim LBL, Priyantha N, Mansor NHM (2014b) Artocarpus altilis (breadfruit) skin as a potential low-cost biosorbent for the removal of crystal violet dye: equilibrium, thermodynamics and kinetics studies. Environ Earth Sci 73:3239–3247
Lim LB, Priyantha N, Hei Ing C, Khairud Dahri M, Tennakoon D, Zehra T, Suklueng M (2015) Artocarpus odoratissimus skin as a potential low-cost biosorbent for the removal of methylene blue and methyl violet 2B. Desalin Water Treat 53:964–975
Lim LBL, Priyantha N, Chan CM, Matassan D, Chieng HI, Kooh MRR (2016) Investigation of the sorption characteristics of water lettuce (WL) as a potential low-cost biosorbent for the removal of methyl violet 2B. Desalin Water Treat 57:8319–8329
Michaels GB, Lewis DL (1985) Sorption and toxicity of azo and triphenylmethane dyes to aquatic microbial populations. Environ Toxicol Chem 4:45–50
Mital A, Kurup L (2006) Column operations for the removal and recovery of a hazardous dyeacid red-27’ from aqueous solutions, using waste materials-bottom ash and de-oiled soya. Ecol Environ Cons 12:181
Mittal A (2016) Retrospection of Bhopal gas tragedy. Toxicol Environ Chem 98:1079–1083
Mittal A, Mittal J (2015) Hen feather: a remarkable adsorbent for dye removal. In: Green chemistry for dyes removal from wastewater: research trends and applications. pp 409–457
Mittal A, Ahmad R, Hasan I (2016a) Biosorption of Pb2+, Ni2+ and Cu2+ ions from aqueous solutions by L-cystein-modified montmorillonite-immobilized alginate nanocomposite. Desalin Water Treat 57:17790–17807
Mittal A, Ahmad R, Hasan I (2016b) Iron oxide-impregnated dextrin nanocomposite: synthesis and its application for the biosorption of Cr(VI) ions from aqueous solution. Desalin Water Treat 57:15133–15145
Mittal A, Ahmad R, Hasan I (2016c) Poly (methyl methacrylate)-grafted alginate/Fe3O4 nanocomposite: synthesis and its application for the removal of heavy metal ions. Desalin Water Treat 57:19820–19833
Mittal A, Naushad M, Sharma G, Alothman ZA, Wabaidur SM, Alam M (2016d) Fabrication of MWCNTs/ThO2 nanocomposite and its adsorption behavior for the removal of Pb(II) metal from aqueous medium. Desalin Water Treat 57:21863–21869
Mittal A, Teotia M, Soni R, Mittal J (2016e) Applications of egg shell and egg shell membrane as adsorbents: a review. J Mol Liq 223:376–387
Naushad M, Mittal A, Rathore M, Gupta V (2015) Ion-exchange kinetic studies for Cd(II), Co(II), Cu(II), and Pb(II) metal ions over a composite cation exchanger. Desalin Water Treat 54:2883–2890
Sabnis RW (2010) Handbook of biological dyes and stains: synthesis and industrial applications. Wiley, Hoboken
Sharma G, Naushad M, Pathania D, Mittal A, El-desoky GE (2015) Modification of Hibiscus cannabinus fiber by graft copolymerization: application for dye removal. Desalin Water Treat 54:3114–3121
Sigma-Aldrich (2012) Methyl violet 2B [material safety data sheet] version 5.0. http://www.sigmaaldrich.com. Accessed 25 Jan 2016
Tang YP, Linda BLL, Franz LW (2013) Proximate analysis of Artocarpus odoratissimus (Tarap) in Brunei Darussalam. Int Food Res J 20:409–415
Tavlieva MP, Genieva SD, Georgieva VG, Vlaev LT (2013) Kinetic study of brilliant green adsorption from aqueous solution onto white rice husk ash. J Colloid Interface Sci 409:112–122
Vachalkova A, Novotný L, Blesova M (1995) Polarographic reduction of some triphenylmethane dyes and their potential carcinogenic activity. Neoplasma 43:113–117
Vilar VJP, Botelho CMS, Boaventura RAR (2005) Influence of pH, ionic strength and temperature on lead biosorption by Gelidium and agar extraction algal waste. Process Biochem 40:3267–3275
Wang M-H, Li J, Ho Y-S (2011) Research articles published in water resources journals: a bibliometric analysis. Desalin Water Treat 28:353–365
Weber W, Morris J (1963a) Kinetics of adsorption on carbon from solution. J Sanit Eng Div 89:31–60
Weber W, Morris J (1963b) Kinetics of adsorption on carbon from solution. J Sanit Eng Div 89:31–60
Zehra T, Priyantha N, Lim LBL, Iqbal E (2015) Sorption characteristics of peat of Brunei Darussalam V: removal of Congo red dye from aqueous solution by peat. Desalin Water Treat 54:2592–2600
Acknowledgements
Appreciation is given to the Government of Brunei Darussalam and Universiti Brunei Darussalam (UBD) for their offer of Graduate Research Studies scholarship.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
All authors declared no conflict of interest.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Kooh, M.R.R., Dahri, M.K. & Lim, L.B.L. Removal of the methyl violet 2B dye from aqueous solution using sustainable adsorbent Artocarpus odoratissimus stem axis. Appl Water Sci 7, 3573–3581 (2017). https://doi.org/10.1007/s13201-016-0496-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13201-016-0496-y