Introduction

Scientific management of groundwater resources is important for its sustainable development. So, there is a need of adequate information about spatio-temporal behavior of water table depths over a region. Water table depth measurements, however, are inherently expensive and time consuming, particularly during the installation phase, which requires drilling a well or a piezometer. Consequently, the number of water table depth measurements that are available in a given area is often relatively sparse and does not reflect the actual level of variation that may be present. Therefore, accurate interpolation of water table depth at unsampled locations is needed for better planning and management.

For mapping of water table depth, the approach of interpolation has either been deterministic, such as inverse distance weighting (IDW) (Gambolati and Volpi 1979; Buchanan and Triantafilis 2009; Sun et al. 2009; Varouchakis and Hristopulos 2013; Arslan 2014) and radial basis function (RBF) (Sun et al. 2009; Arslan 2014) or stochastic, such as ordinary kriging (OK) (Desbarats et al. 2002; Kumar and Ramadevi 2006; Ahmadi and Sedghamiz 2008; Sun et al. 2009; Varouchakis and Hristopulos 2013; Arslan 2014) and universal kriging (UK) (Reed et al. 2000; Kumar and Ahmed 2003; Kumar 2007; Sun et al. 2009, Varouchakis and Hristopulos 2013).

Deterministic interpolation techniques create surfaces from sample points using mathematical functions, based on either the extent of similarity (IDW) or the degree of smoothing (RBF). On the other hand, geostatistical interpolation techniques (kriging) utilize the statistical properties of the sample points. It quantifies the spatial autocorrelation among sampling points and accounts for the spatial configuration of the sampling points around the prediction location (Buchanan and Triantafilis 2009).

In IDW, the interpolated estimates are based on values at nearby location without any spatial relationship among them. This method has been used primarily because of its simplicity (Sarangi et al. 2006) and often applied to interpolate groundwater depth and pollution (Rabah et al. 2011). On the other hand, RBF is one of the primary tools for interpolating multidimensional scattered data. The method’s ability to handle arbitrarily scattered data, to easily generalize to several space dimensions has made it popular in the applications of natural resource management (Sun et al. 2009).

For geospatial interpolation of groundwater depth, researchers use both OK and UK. Prakash and Singh (2000) used the OK technique and determined optimum number of observation wells that can be added to the existing network of the study area for monitoring spatial distribution of groundwater level. Kumar et al. (2005) have emphasized the use of geostatistics for better management and conservation of water resources and sustainable development of any area. Theodossiou and Latinopoulos (2006) worked on spatial analysis on groundwater level using OK to evaluate and optimize the groundwater level observation networks and improvement of the quality of obtained data. Ahmadi and Sedghamiz (2008) used OK to evaluate the spatial and temporal variations of groundwater level and found that groundwater level variations have strong spatial and temporal structure. Nikroo et al. (2010) conducted OK analysis on water table elevation of non-uniformly spaced observation wells in Iran and found a relatively strong spatial relationship between the water table elevations of the wells. Dash et al. (2010) used kriging for optimizing data collection and utility in a regional groundwater investigation and showed that OK is a useful tool to elucidate those areas lacking enough data for developing a water table management network.

Similarly, researches citing the applicability of UK in groundwater depth estimation are also numerous. Kumar and Ahmed (2003) used UK to predict monthly water level variation for a small watershed in a hard rock region of southern India. They attempted to make common variogram(s) for different time periods in a year to estimate water levels on the grids of an aquifer model for calibration purposes. Gundogdu and Guney (2007) evaluated the empirical models to fit into UK for prediction of water table depth. Kumar (2007) applied UK to the command area of a set of canal irrigation projects to show its applicability for optimal contour mapping of groundwater levels. Sun et al. (2009) compared UK with other interpolation methods for assessment of depth to groundwater and its temporal and spatial variations in the Minqin oasis of northwest China. Varouchakis and Hristopulos (2013) also compared between UK and other stochastic and deterministic methods for mapping groundwater level spatial variability in sparsely monitored basins in Greece.

These four widely used interpolation methods (IDW, RBF, OK and UK) have led to the question about which is most appropriate in predicting groundwater depth. Among numerous interpolation methods, no method is uniquely optimal, and so the best interpolation method for a specific situation can only be obtained by comparing their results (Sun et al. 2009). The purpose of this paper is to evaluate and compare the accuracy of four interpolation methods such as inverse distance weighting, radial basis function, ordinary kriging and universal kriging to predict groundwater depth.

Materials and methods

Study area and data collection

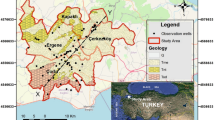
The study area is the National Capital Territory of Delhi lies between 28o24′15″ and 28o53′00″ N latitudes and 76o50′24″ and 77o20′30″ E longitudes covering an area of 1,483 km2. Nearly, 43 % of area is under built-up land, and cultivable land comprises only 10 % of the study area (Fig. 1). The climate is semi-arid with average annual rainfall of about 700.4 mm. Southwest monsoon contributes nearly 84 % of the annual rainfall during the months of July, August and September and the rest is received in the form of winter rain. The average annual temperature is 25 °C with January being the coldest month. April and May are the driest months with relative humidity of about 30 % in the morning and less than 20 % in the afternoon. Soils are deep and calcareous. The geology is marked by quartzite, inter-bedded with mica-schist, belonging to Delhi Super Group. Quartzite occurs in the central and southern part of the area while the quaternary sediments comprising older and newer alluvium cover rest of the area. The groundwater availability is controlled by hydrogeological conditions, characterized by occurrence of different geological formations like Delhi (quartzite) ridge, older and younger alluvium and Yamuna flood plain. For this study, pre-monsoon (May) and post-monsoon (November) groundwater level data of 117 observation wells for 2006 were used. The locations of groundwater observation wells (Fig. 1) were determined with the help of a global positioning system (GPS). A few locations were also cross-checked with a differential GPS.

Fig. 1
figure 1

Map of study area showing observation well locations and present land use

Full size image

Interpolation methods

Inverse distance weighting

Inverse distance weighting (IDW) is a deterministic method traditionally used to interpolate water table depth (Reed et al. 2000). It gives weight to data points such that their influence on prediction is reduced as distance from the point increases. Mathematically, it can be described by considering z (x 0) as the interpolated value, n representing the total number of sample data values, x i is the ith data value, h ij denotes the separation distance between interpolated value and the sample data value, and β denotes the weighting power:

$$z(x_{0} ) = \frac{{\sum\limits_{i = 1}^{n} {\frac{{x_{i} }}{{h_{ij}^{\beta } }}} }}{{\sum\limits_{i = 1}^{n} {\frac{1}{{h_{ij}^{\beta } }}} }}$$
(1)

The choice of this weighting power can significantly affect the estimation quality (Mueller et al. 2001). The optimal weighting power depends on the spatial structure of the data and is influenced by the coefficient of variation (CV), skewness, and kurtosis of the data (Gotway et al. 1996; Mueller et al. 2001).

Radial basis function

Radial basis function (RBF) is a real-valued function whose value depends only on the distance from the origin, or alternatively on the distance from some other point called a center. Any function \(\varPhi\) that satisfies the property \(\varPhi \left( X \right) = \varPhi \left( {\parallel X\parallel } \right)\) is a radial function. The norm is usually Euclidean distance, although other distance functions are also possible. It is possible for some radial functions to avoid problems with ill conditioning of the matrix solved to determine coefficients, since the \(\parallel X\parallel\) is always greater than zero. Among the five different RBFs such as thin-plate spline (TPS), spline with tension (SPT), completely regularized spline (CRS), multiquadric function (MQ), and inverse multiquadric function (IMQ) (Xie et al. 2011), the most widely used RBF that is CRS (Arslan 2014) was selected in this study.

Ordinary kriging

Ordinary kriging (OK) is a linear weighted-average technique, which is unbiased to expected value of errors. It is extensively used to find the linear unbiased estimation of a stationary random field with an unknown constant mean and expressed as follows:

$$\mathop Z\limits^{ \wedge } (x_{0} ) = \sum\limits_{i = 1}^{n} {\lambda_{i} Z(x_{i} )}$$
(2)

where, \(\mathop Z\limits^{ \wedge }\left( {x_{0} } \right)\;\) is kriging estimate at location x 0; Z (x i ) is sampled value at x i ; and λ i is weighing factor associated with Z (x i ). The estimation error is defined as:

$$\varepsilon (x_{0} ) = \mathop Z\limits^{ \wedge }(x_{0} ) - Z(x_{0} ) = \sum\limits_{i = 1}^{n} {\lambda_{i} Z(x_{i} )} - Z(x_{0} )$$
(3)

where, Z (x 0) is the true value of regionalized variable at spatial location x 0 and ε (x 0) is the estimation error. In an unbiased estimator, the expected value of the residual has to be 0.

$$E[\varepsilon (x_{0} )] = 0$$
(4)

The weights sum to unit, so that the predictor provides an unbiased estimation.

$$\sum\limits_{i = 1}^{n} {\lambda_{i} } = 1$$
(5)

In OK, the weighing coefficient λ i can be calculated by solving an optimization problem, whereby, the variance of errors will be minimized, subjected to unbiased condition. Using Lagrange multiplier μ, a constraint optimization problem can be converted to an unconstrained optimization problem.

Universal kriging

UK assumes the model

$$\mathop Z\limits^{ \wedge }(x_{0} ) = \mu (x_{0} ) + \varepsilon (x_{0} )$$
(6)

where, \(\mathop Z\limits^{ \wedge }(x_{0} )\) is the variable of interest, μ (x 0) is some deterministic function and ε (x 0) is random variation (called microscale variation).

The symbol x 0 simply indicates the location (containing the spatial x and y coordinates). The mean of all ε (x 0) is 0. Conceptually, the autocorrelation is modeled from the random errors ε (x 0). In fact, UK is a regression that is done with the spatial coordinates as the explanatory variables. However, instead of assuming the errors ε (x 0) as independent, they are modeled to be auto-correlated. Above-mentioned μ (x 0) is defined as drift. The drift is a simple polynomial function that models the average value of the scattered points (Ahmed 2007). The drift function is given by:

$$\mu \left( {\mathop x\nolimits_{0} } \right) = \sum\limits_{k = 1}^{K} {a_{k} \mathop f\nolimits_{k} (x_{0} )}$$
(7)

where, f k are the basis functions and a k are the drift coefficients (Goovaerts 1997).

If the surface is not stationary, the kriging equations can be expanded, so the drift can be estimated simultaneously, in effect, removing the drift and achieving stationarity. Kriging will estimate the drift, and errors from the drift. The best estimate of the original surface is created by combining the surfaces representing the estimated drift and the estimated errors.

Semivariogram analysis

In case of both OK and UK, the spatial dependence is quantified using semivariogram (Burgess and Webster 1980). The semivariogram γ(h) can be defined as one half the variance of the difference between the attribute values at all points separated by h and expressed as follows:

$$\gamma \,(h)\, = \frac{1}{2\,N(h)}\sum\limits_{i = 1}^{N\,(h)} {[Z\,(x_{i} + h) - Z(x_{i} )} ]^{2}$$
(8)

where, γ(h) is the semivariogram expressed as a function of the magnitude of lag distance or separation vector h, and N(h) is the number of observation pairs separated by distance h.

The experimental semivariogram γ(h) can be fitted to different theoretical models such as Spherical, Exponential, Linear or Gaussian to determine three semivariogram parameters, such as nugget (C 0), sill (C 0 + C) and range (A 0) (Issaks and Srivastava 1989). The value of the semivariogram for distances beyond the range is called the sill. It is often composed of two parts: a discontinuity at the origin, called the nugget effect, and the partial sill, which when added together gives the sill. The nugget effect can be further divided into measurement error and microscale variation. The nugget effect is simply the sum of measurement error and microscale variation and, since either component can be zero, the nugget effect can be comprised wholly of one or the other. The distance at which the semivariogram levels off to the sill is called the range (Johnson et al. 2001).

Model selection, semivariogram parameters for kriging and power function selection for IDW

The data sets were subjected to exploratory analysis to identify the outliers and carried out different transformations such as log normal and square root to ensure normal distribution. After this, semivariogram analysis was done using GS+ software. The best-fit theoretical model was obtained based on maximum R 2 and minimum RSS. The lag size and the number of lags in conjunction with the model functions were selected using trial and error approach. The corresponding sill, nugget, and range values were observed. However, for IDW, after ensuring normality of the data, assessment of the optimal power function was determined by testing a series of powers ranging from 1.0 to 4.0, which is the range in which the optimal power commonly lies (Kravchenko 1999). The power was increased in increments of 0.5 to determine the value that minimizes the RMSE of the prediction of water table depth.

Performance comparison of IDW, RBF, OK and UK

Generally, correlation-based and error-based measures are used to evaluate the goodness-of-fit of the models. The correlation-based measures considered in this work include the coefficient of determination (R 2), coefficient of model efficiency (E) and index of agreement (I A).

$$R^{2} = 1 - \frac{\text{ESS}}{\text{TSS}}$$
(9)

where ESS and TSS are the error sum square and total sum square of water table depth data set.

The coefficient of model efficiency (E) is expressed in the following equation (Nash and Sutcliffe 1970):

$$E = 1 - \frac{{\sum\limits_{i = 1}^{N} {(O_{i} - S_{i} )^{2} } }}{{\sum\limits_{i = 1}^{N} {(O_{i} - \mu_{0} )^{2} } }}$$
(10)

where O i and S i are the observed and simulated water table depth at ith location (m) and N is the number of observations. The coefficient of efficiency is a dimensionless measure, ranges between −∞ and 1 where higher values denote better agreement.

As the NS model efficiency is biased to the higher values, the index of agreement (I A) is used and expressed as below (Legates and McCabe 1999):

$$I_{A} = 1 - \frac{{\sum\limits_{i = 1}^{N} {(O_{i} - S_{i} )^{2} } }}{{\sum\limits_{i = 1}^{N} {\left( {\left| {S_{i} - \mu_{0} } \right.| + \left| {\left. {O_{i} - \mu_{0} } \right|} \right.} \right)^{2} } }}$$
(11)

where μ 0 is the average observed water table depth. The index of agreement varies from 0 to 1 with higher values indicating better agreement between the simulated and observed depths.

The error-based measures used in the study include the root-mean-square error (RMSE), the mean error (ME), and the mean relative error (MRE). The RMSE is a measure of the accuracy of prediction. Accurate predictions have a value close to zero. The ME represents the bias of prediction, and it should be close to 0 for unbiased methods. These measures can be computed using the following formulas:

$${\text{RMSE}} = \sqrt {\frac{{\sum\limits_{i = 1}^{N} {(O_{i} - S_{i} )^{2} } }}{N}}$$
(12)
$${\text{ME}} = \frac{{\sum\limits_{i = 1}^{N} {O_{i} - S_{i} } }}{N}$$
(13)
$${\text{MRE}} = \frac{\text{RMSE}}{\Delta }$$
(14)

where ∆ is the range and equals the difference between the maximum and minimum observed water table depth. MRE is an important measure since both RMSE and ME do not provide a relative indication in reference to the actual data.

Result and discussions

Distribution of spatial data

The outliers present in the data set were first removed. Kolmogorov and Smirnov test was carried out to ascertain the normal distribution of the data. K–S test revealed that the data were not normally distributed. In addition, skewness values of histograms of the spatial water table depths were also used to check the normality of the data set. Skewness values of the histograms regarding all the data sets and the descriptive statistics are given in Table 1. The skewness values in the first column were obtained without making any transformation. As these values were not close to zero, it was concluded that the data set was not normally distributed. To adjust the water table depth values to the normal distribution, log normal transformation was carried out and the histogram was formed again. The skewness values of the lognormally transformed data indicated that lognormal transformation can make the data normal. Similar finding was also observed by Dash et al. (2010).

Table 1 Descriptive statistics with different skewness states of observed water table depths
Full size table

Spatial structure of water table depth

The best-fit theoretical semivariogram models were tried and in all the data sets, exponential model resulted maximum R 2 and minimum residual sum of square (RSS) values, and therefore, considered as the best-fit model (Dash et al. 2010). The parameters of the best-fit exponential model for all the data sets are given in Table 2. Nugget and sill were very low. Nugget value was 0.123 and 0.292 and sill value was 1.222 and 2.309, respectively, for pre- and post-monsoon data. Nugget effect and nugget-to-sill ratio were used to classify the spatial dependence (Cambardella et al. 1994) of the variables. According to Liu et al. (2006), a variable is considered to have strong spatial dependence if the nugget-to-sill ratio is less than 0.25, and has a moderate spatial dependence if the ratio is between 0.25 and 0.75; otherwise the variable has a weak spatial dependence. So, in our case, the water table depths were highly spatially correlated. The range was found 16.45 and 35.88 km, respectively, for pre- and post-monsoon depth and also did not exhibit any trend. From the range values it can be inferred that to predict water table depth of Delhi, the maximum sampling distance should be 16.45 km. In our case, the sampling distance was less than 4 km, which was quite adequate.

Table 2 Summary of semivariogram parameters of best-fitted theoretical model to predict water table depth
Full size table

For IDW method, after normalization of dataset, the power function was optimized and the cross-validation dataset was analyzed. In this study, the optimizing parameter of the weight function was taken as 2.0.

Performance analysis

Because the primary objective of this investigation was to compare interpolation methods, first the effect of interpolation methods on accuracy was considered. The most striking result along this line was that the two kriging methods outperformed the IDW method to predict groundwater table depth for both the seasons, and RBF performed better than OK. This agreed with the findings of several authors who have made comparisons among interpolation methods (Zimmerman et al. 1999; Sarangi et al. 2006; Kumar 2007; Sun et al. 2009; Arslan 2014), but contradicted the findings of several other such authors (Weber and Englund 1992; Gallichand and Marcotte 1993; Declercq 1996). Our study strengthened the fact that the performance of kriging was superior to IDW. Of course, kriging has several other advantages, but those were not performance related. The underperformance of IDW may be due to the fact that it could not distribute the weights properly to arrest the drifting effect of water table depth. The data distribution may be another reason, but in normal condition observation wells used to be distributed randomly. So, IDW may underperform in normal practical situation.

Quantitative comparison of the interpolation methods was obtained by comparing the performance of the theoretical models. Figure 2 depicts the scatterplots of the observed versus predicted water table depth obtained by IDW, RBF, OK and UK methods during pre- and post-monsoon seasons. To facilitate the assessment, error bounds were provided. Error bounds were calculated by adding (and subtracting) the percentage of error to the simulated and observed values and then drawing the corresponding upper and lower lines. The solid line represented the 1:1 line and the dashed lines represented the ±15 % and ±30 % error bounds. The majority of the points were within the ±30 % error bounds. In case of IDW and RBF prediction, the data points below the 1:1 line signified that the model underestimated the groundwater depth at these locations and actual depth might be more than the predicted. On the other hand, the scatter points for OK and UK showed that few points were lying above the 1:1 line, indicating their overestimations by the models. The model performances for RBF, OK and UK were better when compared to the IDW results. In RBF, OK and UK scatterplots, majority of the data points were within the ±15 % error bounds and very few points were within ±30 % error bounds.

Fig. 2
figure 2

Scatterplots of the observed versus predicted water table depth obtained by inverse distance weighting, radial basis function, ordinary kriging and universal kriging methods for a Pre-monsoon and b Post-monsoon seasons. The solid line represents the 1:1 line and the dashed lines represent the ±15 and ±30 % error bounds

Full size image

Assessment measures of model performance are summarized in Table 3. High values of coefficients of determination, coefficients of model efficiency, and indices of agreement suggested a good match between observed and predicted water table depth. Among the four interpolation methods, the performance of UK was best and OK performed considerably better than IDW. The interesting fact was that RBF performed better than OK. This result is in conformity with the result obtained by Arslan 2014. Not only the model performance indicators, but the errors also confirmed the above fact. Low RMSE and ME for all the interpolation methods indicated their applicability to predict water table depth, and the superiority of UK over all other methods was also well established from its lowest error values. The MRE, which provided relative errors of the predicted data in reference to the actual data, was also very low and lowest for UK. Further analysis showed that 52, 67, 73 and 77 % of the predicted water table depths were within an error margin of ±15 % for IDW, OK, RBF and UK, respectively (Fig. 2).

Table 3 Comparison of the efficiencies and errors of the interpolation methods to predict water table depth
Full size table

The superiority of UK, RBF and OK over IDW to predict water table depth was well established by this study, but to quantify the relative performance, the per cent improvement of UK, RBF and OK over IDW was also calculated. From Table 4, it was clear that OK, RBF and UK yielded an RMSE 24.37–30.68, 26.36–28.15 and 48.64–53.58 % lower than IDW. The average decrement of RMSE of OK, RBF and UK over IDW was 27.52, 27.66 and 51.11 %, respectively. Similarly, the reduction of MRE for OK, RBF and UK over IDW was 27.49, 35.34 and 51.28 %, respectively. The R 2 value of OK, RBF and UK showed an increment over IDW with a tune of 14.21, 16.12 and 21.36 %, respectively. The drawback of IDW was the inability to account for the intersample variation that may occur in the water table depth. That is, the predictions using IDW were based solely on the values of neighboring sampling points and the weight assigned. The drawback of OK was that its predictions were based on spatial structure of water table depth measurements (Buchanan and Triantafilis 2009). The water table depth may not be a stationary variable, so, interpolation through OK obviously added some error to the prediction. The drift of water table depth towards the direction of its flow can be arrested by UK, resulted the best prediction (Kumar 2007).

Table 4 Summary of the performance of interpolation methods in terms of improvement over inverse distance weighting
Full size table

One noteworthy finding was that the ME values of OK and UK were negative (Table 3). This was not an unusual result, considering the unbiased nature of the geostatistical methods. The negative ME suggested that the theoretical model was overestimating the water table depth (i.e., observed < predicted). For IDW and RBF prediction, ME values were positive, indicating their underestimation of water table depth. This confirmed the finding obtained through scatterplots analysis (Kumar 2007).

Visualization of prediction

To visualize the spatial distribution of predicted water table depth, maps were generated. This has been undertaken by simply performing the interpolation method using UK as it has given best prediction. The interpolated maps (Fig. 3) indicated that greater depths (>20 m) were predicted in the south-eastern part of the study area and shallower depths (<20 m) were predicted in central, western and northern parts of the study area. The distribution at shallower depths was characterized by large, spatially contiguous contours.

Fig. 3
figure 3

Predicted water table depth map of Delhi interpolated through universal kriging for a Pre-monsoon and b Post-monsoon seasons

Full size image

The area-wise distribution of various water table depth within the study area was also calculated using the best interpolation method among the four, i.e., UK (Table 5). It was clear that only 20–23 % area is mainly concentrated in the south-eastern part of the study area having water table depth more than 20 m. Interestingly, there was very little or no seasonal variation of water table in this pocket. This was because the pocket lie in the Chattarpur basin surrounded by quartzite ridge which has made the basin isolated from surrounding groundwater flow paths and the groundwater recharge through surface was very low due to urbanization.

Table 5 Predicted areas interpolated through universal kriging under different water table depth
Full size table

Figure 4 illustrates the isodepth-area curves for UK estimation. It seems to be a good way for quantification of the maps that look similarly. It was seen that up to isodepth line 20 m, the curves remained close to each other with higher slope, but after this, they moved nearly parallel to each other with a gentle slope. Developing such curves and integrating them with the geostatistically derived maps help the water managers to make appropriate decision on how to exploit the aquifer; for instance, which crops or cultivation patterns are suitable for a specific year and which regions are critical that the farmers should be aware of (Ahmadi and Sedghamiz 2008). In the present study, it has been found that during pre-monsoon season nearly 720 km2 areas have groundwater depth of ≤10 m which increased to nearly 790 km2 during post-monsoon season. In this way, the local agricultural manager or advisor may suggest the farmers of the study area to change their cropping pattern during that particular season.

Fig. 4
figure 4

Groundwater isodepth-area curves for pre- and post-monsoon seasons of 2005 and 2006 obtained by universal kriging interpolation method

Full size image

Conclusions

This paper presents a comparison of stochastic (OK, UK) and deterministic (IDW, RBF) interpolation methods for groundwater level prediction. The cross-validation measures were used to compare various interpolation methods. In Delhi, IDW, RBF, OK and UK interpolation methods satisfactorily predicted the spatial variation of water table depth for both the seasons, and OK and UK methods outperformed the IDW method. RBF performed better than OK to predict depth to groundwater table. Among the kriging methods, UK performed better than OK to predict water table depth. IDW and RBF methods underestimated whereas OK and UK overestimated the water table depth. The isodepth-area curves indicated that there is greater possibility of exploitation of groundwater up to a depth of 20 m.