1 Introduction

Railway are the important drivers of the today’s society. Railways have been facing higher demands from the public and from industries due to expansion in adaptation, population growth and traffic flow. In the context of Swedish railways, there are expected into increase 3% for passenger traffic and 1% in freight traffic up to 2050 annually. To meet these demands, the infrastructure managers need to plan to achieve higher requirements; reduce the unexpected failures, increase the train capacity and reduce in cost.

The recent study (Analysis 2014) on the Swedish railway sector identifies the key problems within the existing network as (1) a backlog of track infrastructure maintenance, (2) capacity problems, and (3) punctuality. The first problem, maintenance, has been given less consideration because of low investments hence there is an excessive need for improved maintenance (Vredin 2013). With 70% single tracks and passenger and freight mix of traffic, Swedish rail infrastructure is vulnerable to traffic disturbances and lead to huge consequences in any part of the rail network.

The traffic planning is in general scheduled for 18 months in Swedish rail infrastructure. However, due to maintenance activities such as repair/replace/overhaul, this plan will change for shorter durations as well. Within the traffic planning, the Switches and Crossings (S&Cs) or turnouts are the one of the most important assets as it acts as a network switch to choose between two or more routes. Also, Nissen (2009), Ossberger and Bishop (2010) and Parahy (2011) studies showed that the failure of S&Cs led to higher costs. Hereafter, the condition of these S&Cs is crucial for planning because inoperable status leads to disruption of the traffic in two or more lanes. The condition of S&Cs can be predicted within short duration (nowcasting) or for longer durations (forecasting).

Hence, the purpose of this study is to predict the present and future status of the S&Cs for the effective traffic and maintenance planning within traffic management system. Section 1 presents the definitions of nowcasting and forecasting. Section 2 provides the background of Swedish railway traffic management system, provides the basis of nowcasting and forecasting in failure and no-failure scenarios and selection of S&C as main critical asset. Section 3 implements non-Homogenous Poisson process for S&C and its results are shown in Sect. 4.

1.1 Nowcasting and forecasting

In general, the term “forecasting” known to most of the local and global community, the term “nowcasting” is not known to, especially in railway. But this is predominantly of significant importance in various research areas especially in meteorology, economics, medicine and environmental sciences. Its approval to the railway community needs to be clarified with appropriate connotations so that it is in aligned for applicability (Oneto et al. 2017).

The term “nowcasting” frequently applied in the field of Meteorology, where it is denoting the process of providing weather data and forecasts from zero to few hours ahead (e.g. 30 min (Rasmussen et al. 2001), 1 h (Sokol 2006), 2 h (Browning and Collier 1989), 3 h (Shao and Lister 1996) (Sokol and Pešice 2009), 6 h (Isaac et al. 2014). In general, the term “nowcasting” is used when dealing with sudden events (e.g. thunderstorms, lightning, tornados) that cannot be predicted by traditional forecasting approaches and can be unsettling or represent a safety threat. Hence, the nowcasting is used for discriminating from “forecasting” both in means of timeframe (forecasts are long-term predictions, nowcasts are short-term predictions) and of methodology (nowcasts are produced with different approaches and algorithms, respect to forecasts).

The usage of “nowcasting” can be related to: a shorter span with respect to “forecasting”, a same or different approach or algorithm for execution the prediction of the value. The fact that the data used for the both approaches can be estimated with detailing in terminology so that it is of specific interest for predicting the status for railway asset’s optimization, planning and scheduling (Mantis 2017).

The term is vague enough to be stretched to cover all these slightly different meanings, so the need of a formal definition is not necessary nor, probably, useful. A reasonable simple definition could be adopted in the framework of the In2Rail project for differentiating “forecasting” and “nowcasting” processes (In2Rail 2017; Jiménez-Redondo et al. 2017):

  • Nowcasting: The process of exploiting past and present uncertain or incomplete data to make deductions about the present.

  • Forecasting: The process of exploiting past and present data to make deductions about the future.

Note that, as it is assumed that forecasts would be in any case uncertain, because of the uncertainty linked to any event that will happen in the future, there is no need to specify that the data for forecasting could be uncertain or incomplete. In this unfortunate case, the accuracy of the forecast would obviously be low, but this could happen anyway, even with ideal data, while this is not true for nowcasting, where ideal data would result in perfect nowcasts. The following term is used in this context.

Nowcasting should be used by the train dispatcher to select the best initial route to be locked for the train. The best route will be selected by evaluating measurements and estimations of the asset status giving the probability of each rout to provide the required service. By extending this analysis to other sections along the complete route to the destination, beyond the first locked section, the nowcast transforms into a forecast. The forecast can further be extended up to more than 18 months into the future.

If the nowcast and the forecast concepts should be converted into the time domain there are some parameters that have to be considered. Since the train will occupy the track later the nowcasting has to consider the time between 0 and 10 min (approximately). The length of the time span mainly depends on train length, train speed and length of the section.

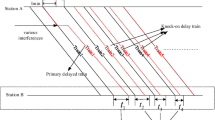
Forecasting needs to be carried out on the sections that are ahead of the locked route as shown in Fig. 1 . The time span of forecasting varies after the time span of locked route to several months that depends on the requirements, length and planning of the train. After locking the first route, the group of track sections also need to be forecasted of asset condition up to the destination for e.g., 1 day. In the diagram shown, the track route extended from T2 to T3 is the first level of forecasting. Once this information is sent to the train dispatcher, then the status of this group of track sections is known that has good asset condition and lower level of probability of failure. For the second level of forecasting, the length of time span varies from 1 day to 14 days. By knowing the condition of the asset prior this long time, necessary maintenance actions must be carried out on S&Cs. For the third level of forecasting, within time span of 14 days to 18 months, maintenance actions can be carried out as well as scheduling of the maintenance vehicles also to be intimated to train management system (TMS) for the appropriate time planning. This time can also be used to carry out for procuring, logistics and cost-effective solutions.

Fig. 1
figure 1

Nowcasting and Forecasting of routes

Full size image

2 Background of Swedish railway

2.1 Objectives

The main objective is to nowcast and forecast the probability of failure of switches and crossings based on the inspections and maintenance actions for traffic planning.

  • To identify the condition of switch

  • To calculate time to restoration if there is a failure of switching and crossing

  • To reduce the probability of risk by sending the train to the best alternative route

2.2 Swedish railway TMS

The traffic planning incorporates nowcasting and forecasting with the following factors:

  • for statistics into traffic management

  • to combine different disciplines within the Swedish rail administration

  • maintenance demand due to traffic density and characteristics

  • maintenance demand according to the use of the infrastructure

  • traffic management affected by a feed-back loop from/to every business area

The time perspective for the use case (and the time to restoration) can be from a few minutes up to several months. In the longer time perspectives (more than about 24 h), the main user of the information may rather be the production planning department than the TMS-users. However, the timeframe between the needs of the operational control (TMS-users) and the production planning dependent on the organization of the Infrastructure Manager (IM) in Fig. 2.

Fig. 2
figure 2

Illustration of failure: Production plan (graphical timetable) with infrastructure failures and estimated restoration times on a single-track line

Full size image
  1. 1.

    TMS-user identify in the production plan that a part of infrastructure is marked as out-of-order, so that a segment of the infrastructure cannot be used.

  2. 2.

    TMS-user inspects the traffic that corresponds to the restoration of the infrastructure and makes appropriate priorities to ensure that restoration time can be fulfilled.

  3. 3.

    If the infrastructure component is faulty but still usable then the error is indicated in the production plan.

  4. 4.

    The TMS-user looks at the estimated “time-to-restoration” for the affected infrastructure segment.

  5. 5.

    User adjusts the production plan to take the uncertainty of restoration time into account.

2.3 Switching and crossings

S&Cs has been selected based on the opinion from the TMS with respect to the components responsible for the largest disturbance in the train management process. Failure of this component has a larger impact on the planning systems and possibility to lock train routes, causing disturbing dominant effects in the surrounding network.

Switches and crossings (or turnouts) are a collective term like turnout where S stands for switching part and C stands for section where the rails are crossings each other as shown in Fig. 3. Switches and Crossings are mechanical, electrical and signaling systems in the railway. Their function is to be able to carry trains into two (or more) tracks in a safe way. When the switching mechanism is set up from the control system, the switch blade switches from one position to another position for diverting the train in opposite direction. The switch is locked to new position when a control signal from the locking procedure has been received. When the control signal has been received by the TMS, the asset can be utilized for an intended train route. This switching mechanism can be failed due to many types of failure modes that malfunctions the switching procedure. In some cases, called as partial failure, the switch retains in a right-side position and locked but cannot be controlled with switching mechanism.

Fig. 3
figure 3

Illustration of switches and crossings (Mishra et al. 2017)

Full size image

2.4 Failure modes of S&Cs to nowcast and forecast

S&Cs are crucial subsystems in the railway that allows the trains to change from one track to another track. By enabling trains to move, and allowing slower trains to be overtaken, S&Cs are provided to achieve higher capacity both on a single track and on double track lines. Failure modes for S&Cs are shown below (Esveld and Esveld 2001):

  1. 1.

    Drive mechanism failure: A failure in the drive mechanisms will disable any movement of the switchblade. This failure mode is considered as a semi-failure since the switching function could still be in an upstate if no movement of the switch blade is required before the locking of the trail route. This requires that the control in signaling that the blade is in a correct position and locked.

  2. 2.

    Control circuit failure: If the switch blade is in the right position but the control signal has failed to detect this, a control failure occurs. For some switch types, it is however allowed to manually inspect the blade position and pass the switch. Therefore, this failure could be considered as a semi-failure.

  3. 3.

    Snow and ice problems: During winter, the number of failures increases with up to 50%. Most of this is related to weather conditions but is also more common early in the winter that heating element fails.

  4. 4.

    Cracks: Cracks will evolve over time and are dependent on the load cases. If the crack reaches predefined limits, a failure occurs. Cracks can appear in different parts in the S&C but especially in the crossing nose where impact forces are high. There is only measured information on rail and switch rail, but not for the crossing.

There are various maintenance actions that can be performed for an S&C to retain its function. For minimal repair and short term, the lubrication is performed on the slide bars for every month. For maximum repair and longer term, surface welding, tamping and grinding are performed after a period of 1–5 years. For longer than 5 years, overhaul or renewal of subsystems such as switch blades, crossing and renovating of point machines are performed that are expensive and time consuming. Most of the maintenance decisions are taken based on an inspection report. Usually, regular inspections are carried out between 1 and 3 months. In some other countries, visual inspection is performed for every week on the most critical S&Cs.

3 Methodology

3.1 Modelling

Some researchers are interested to study the wheel/rail interaction at turnouts. Andersson and Dahlberg (1998) emphasized on wheel/rail impacts at turnouts. Gurule and Wilson (2000) developed simulation methodology for wheel/rail interaction for South African Railways. Kassa et al. (2006) developed simulation framework for dynamic interaction of train and turnout. Casanueva et al. (2014) studied the influence of S&Cs on wheel profile evolution. Kaewunruen (2014) provided structural deterioration via dynamic wheel/rail interaction.

Some more researchers are considered maintenance modelling using condition monitoring techniques for different countries. Zarembski et al. (2006) developed maintenance indices. Zwanenburg (2009) presented the modelling for degradation process of S&Cs for maintenance and renewal planning for Swiss Railway. Nicklisch et al. (2010) studies the geometry and stiffness optimization and simulation of S&C degradation. Cornish et al. (2012) developed a methodology for predictive maintenance using condition monitoring for Network Railways. They observed that there are higher peaks of strain at the crossing nodes and switch blade.

Garcí et al. (2003) and Pedregal et al. (2004) developed Reliability Centered Maintenance (RCM) approach for maintenance of S&Cs in UK. Yilboga et al. (2010) predicted the failures in turnouts using time delay neural networks. Eker et al. (2012) developed support vector machine (SVM) framework. Atamuradov et al. (2009) failure diagnostics of point machines. Guclu et al. (2010) predicts using autoregressive moving average. Mishra et al. (2017) predicted the status of S&C using track geometry degradation. The more recent studies include Kieu (2018) for analytical modelling of point process, Babishin and Taghipour (2019) for maintenance effectiveness, Das et al. (2020) for track restoration and Zarezadeh and Asadi (2019) for coherent systems. There are not many reliability studies of S&C which exploits data related to failures and maintenance records. Hence, this paper utilizes application of Non-homogenous poison process (NHPP) for predicting the failure in S&Cs.

3.2 Problem formalization

The nowcasting for the probability of failure of S&Cs can be calculated as shown in flowgraph depicted in Fig. 4. There are different data sources available to calculate the forecasting. These data sources are asset register (BIS), failures (Ofelia), Optram (Track geometry), weather (SMHI), maintenance (BESSY), interlocking system (DS-Analys) and traffic information (STIG) (Thaduri et al. 2015). This aggregated data must be cleaned before processing according to the S&C within track section. This aggregated data is useful to analyze and find the statistical insights and behavior of S&Cs.

Fig. 4
figure 4

Proposed process flow of nowcasting scenario

Full size image

The analysis of the problem can be carried out in two stages; one is statistical analysis and second is the nowcasting and forecasting prediction. The statistical results show an insight to the different types of failures and maintenance actions carried out on the S&Cs. This will help in TMS to give a quick judgement on what are the possible dominant failure modes/causes that can disrupt the traffic. From the available data, the nowcasting and forecasting of a specific S&C in a track section can be found out by using data driven methods using reliability modelling. To obtain the probability of failure, a non-homogenous Poisson process (NHPP) was used to predict the nowcasting. Furthermore, the nowcasting of further inputs such as weather forecasts from the previous data can also be prediction using regression modelling, but it is not that dominant to influence the predictions.

3.3 Proposed solution

The assets chosen in this scenario, the switches and crossings, are the repairable systems. The probabilities can be estimated by using non-homogenous Poisson process-Power law models for rerouting the traffic by TMS. This can be achieved by analyzing the life data from the growth curves. The mean number of repairs and the rate of occurrence of failure (ROCOF) over time can be calculated by using a power-law process or a homogeneous Poisson process. The developed models based on the Power Law NHPP are useful to predict the nowcast for present condition (Minitab 2017).

3.3.1 Non-homogeneous Poisson process (NHPP)

A nonhomogeneous Poisson process with an intensity function that represents the rate of failures or repairs (Crow 1975). There are several studies that utilizes NHPP for repairable systems. Hossain and Dahiya (1993) and Zhao and Xie (1996) for software reliability, Guida et al. (1989) for NHPP with Bayes inference and Yanez et al. (2002) for general renewable process using Monte Carlo Simulation, Majeske (2007) for automobile warranty claims and Garmabaki et al. (2016) for aircraft fleet. In Railway industry, there were only few studies, Pievatolo et al. (2003) for underground trains, Panja and Ray (2007a) for point machines, Panja and Ray (2007b) for track circuit signaling, Chattopadhyay and Kumar (2009) for rail degradation model and Garmabaki et al. (2016) for frequency converters.

The power-law process can model a system that is improving, deteriorating, or remaining stable. This model can predict failure/repair times that have an increasing, decreasing, or constant rate. The repair rate for a power-law process is a function of time. The non-homogeneous Poisson process (NHPP) differs from the HPP by the fact that the ROCOF varies with time. The condition to fulfil for a counting process N(t), t ≥ 0 to be an NHPP are: − N(0) = 0; − N(t), t ≥ 0 has independent increments (not in accordance with definition but assumed anyway);—the number of events (failures) in any interval ti − ti−1,(i = 1,…, n) has a Poisson distribution with mean \( \mathop \smallint \limits_{{t_{i - 1} }}^{{t_{i} }} v\left( t \right)dt \), we have (Basile et al. 2004):

$$ P(\left( {N\left( {t_{i} } \right) - N\left( {t_{i - 1} } \right) = j} \right) = \frac{{{ \exp }\left( {\mathop \smallint \nolimits_{{t_{i - 1} }}^{{t_{i} }} v\left( t \right)dt} \right)\left( {\mathop \smallint \nolimits_{{t_{i - 1} }}^{{t_{i} }} v\left( t \right)dt} \right)^{j} }}{j!} $$
(1)

where i = 1,…, n; j ≥ 0; where i and j are identifiers for failure times

The expression of the reliability function is:

$$ R\left( {t_{i} - t_{i - 1} } \right) = \exp \left( {\mathop \smallint \limits_{{t_{i - 1} }}^{{t_{i} }} v\left( t \right)dt} \right) $$
(2)

where i = 1,…, n; j ≥ 0;

ROCOF for the power law is

$$ v\left( t \right) = abt^{t - 1} $$
(3)

where a and b are indicators of the model. And the expected number of failure is

$$ v\left( t \right) = abt^{t - 1} $$
(4)

Because of the polynomial nature of the ROCOF, this model is very flexible and can model both increasing (b > 1 or a < 0) and decreasing (0 < b < 1 or 0 < a < 1)) failure rates. When b = 1 or a = 0, the model reduces to the HPP constant repair rate model (NIST 2017). Each of these tests uses the Bartlett’s modified likelihood ratio test whenever possible.

The hypotheses for these tests are:

H0: all the shapes (or scales or Mean Time Between Failure (MTBF)) are equal

H1: at least one of the shapes (or scales or MTBFs) is different

3.3.2 Probability of failure

Parametric Growth Curve is used to estimate the probability of failure within a given time frame. The estimated mean cumulative function, MCF,

$$ MCF = \left( {\frac{t}{\theta }} \right)^{\beta } $$
(5)

where t = the time since the start of the test, β = the estimated shape parameter, θ = the estimated scale parameter. The probability that at least one failure will occur between now (t) and the next t1 h is:

$$ P\left( {X \ge 1} \right) = 1 - e^{{ - \left( {MCF\left( {t + t1} \right) - MCF\left( t \right)} \right)}} $$
(6)

where X is the number of failures in the time interval (t, t + t1].

4 Nowcasting and forecasting results

4.1 Statistical results

The below results are obtained from the aggregation of available data sources obtained from Trafikverket. The figures from Figs. 6 and 7 show the dominant failure modes, causes, actions and interdependencies of failures. This information will provide a decision support to TMS for quick action possible outcomes of the failure to reduce the time to restoration. Because, the identification of the problem, in case of less information, can be useful to TMS to judge the approximate time to restoration and to get the asset in working condition.

4.1.1 Causes versus actions

The most Cause-Action pairs as shown in Fig. 5 are:

Fig. 5
figure 5

Interaction of causes and actions of S&Cs

Full size image

  • Snow–Snow clearance

  • Rinsing-material fatigue

  • Unknown cause-cleaning

The cause-action pair can provide the combination of different causes and possible actions taken on the S&Cs. As illustrated in the figure, these action pairs are dominant of all other combinations. Due to the environmental condition of Swedish network, it is shown from the results that these S&Cs are subjected to frequent failures due to snow.

4.1.2 Failure type versus subsystem corrected

The most failure type-subsystem corrected pairs as shown in Fig. 6 are

Fig. 6
figure 6

Failure type versus subsystem corrected pairs for S&Cs

Full size image

  • Point machine and bars-not possible to define

  • Heating system and broken

  • Switch blade detection because of broken materials.

There is lot of uncertainty on the point machine bars as what might be the reason for failure. This need further research to consider engineering solutions to reduce the frequency of the failures. The other systems are mostly failed because of the broken materials due to overstress and excessive usage of the subsystems.

4.1.3 Failure number versus down time of S&Cs

The distribution of time to restoration is shown in Fig. 7. The time to restoration of S&Cs is 90% in the range up to 2 h. There are some failures delayed > 1000 min due to less importance or no traffic disruption. Because of the distribution of the time to restoration, it has been presumably estimated that the TMS needs approximately two hours to plan for maintenance actions of S&Cs to do repair/replacement depending upon the traffic density.

Fig. 7
figure 7

Time to restoration of failures of S&Cs

Full size image

4.2 Nowcasting and forecasting predictions

For the demonstration purpose, the nowcasting predictions of the S&Cs are carried out for a track section 414. There are 13 S&Cs. The predictions can be carried out by using the Weibull distribution (Power Law) with Maximum Likelihood Estimation (MLE).

A nonhomogeneous Poisson process with an intensity function can be used for modelling probability of failure (PoF) of S&C since the power-law process can model a system that is improving, deteriorating, or remaining stable. The probability of failure can be estimated by using the (Majeske 2007):

$$ PoF\left( t \right) = 1 - exp\left[ {1 - \left\{ {\left( {\frac{T + t}{\eta }} \right)^{\beta } - \left( {\frac{T}{\eta }} \right)^{\beta } } \right\}} \right] $$
(7)

where η = scale parameter and β = shape parameter, T = Last occurrence of failure and t = time from the Last failure. The failure corresponds to failure record of any subsystem in an S&C system that is stored in failure database, Ofelia. The probability density function (PDF) for a 2-parameter Weibull distribution is

$$ f\left( t \right) = \frac{\beta }{\eta }\left( {\frac{t}{\eta }} \right)^{\beta - 1} e^{{ - \left( {\frac{t}{\eta }} \right)^{\beta } }} $$
(8)

where t is the failure time, β is the shape parameter and η is the scale parameter

The failure probabilities for all S&Cs are calculated from the above equation. There are 18 S&Cs in track section 414 with different failures as represented in event plot in Fig. 8. The duration of failure events is selected from the time window of year 2013 to mid of 2016 (means 0 to 1,800,000 min). The parameter estimates from Weibull distribution (Power Law) with Maximum Likelihood Estimation (MLE) is extracted from MINITAB is shown in Table 1. The Weibull parameters obtained for n = 18 S&Cs are scale parameter, η18 is 164,118 and shape parameter, β18 is 0.9049 (needs further validation). The test for equal shape parameters suggests that there is not enough proof that the systems came from same population with different shapes (P value = 0.245). The pooled estimate of the shape is valid. The tests for trend are all significant (P value = 0.000) from Anderson–Darling test. These tests showed that non-Homogenous Poisson process is applicable for modelling PoF for failure data of S&Cs in track section 414.

Fig. 8
figure 8

Event plot for time to failure (TTF) in mins

Full size image
Table 1 Extraction of parameters from Minitab
Full size table

The probability of failure (PoF) of S&Cs are calculated from the present instant (PT = 1,800,000) to 12,000 min (for example, time span for nowcasting and forecasting) are shown in Fig. 9. Here, the probability of failure of an S&C is determined by considering the time of last failure, number of failures and time between failures of a particular S&C. The nowcasting predictions of probability of failure of S&Cs are tabulated in Table 2. The predicted probability of failures shown in Fig. 9 can be utilized by TMS to reroute the train for an S&C within a network. The model will also be recalculated in the event of maintenance action or failure.

Fig. 9
figure 9

PoF of S&Cs from the present instant (PT = 1,800,000 min) to 12,000 min

Full size image
Table 2 Probability of failure from last failure until present instant + 12,000 min
Full size table

5 Conclusion

For re-routing trains by TMS, the above nowcasting predictions can provide an additional information of probability of failure of S&Cs within a network. The probability of failure for the next t + 200 h (approx. 10 days) nowcasting predictions will be helpful in a case where TMS has to choose between two possible meetings stations for two trains for shorter term decision. However, the model can be applied for the required time frame for nowcasting purposes. If the interlocking system status of two S&Cs are similar, then the TMS can decide the possible meeting station, which has less probability of failure. For the maintenance managers, the one with high probability of failure and it can disrupt the traffic has higher priority to take immediate action to make best time to restoration. In addition, the results need to be validated on the field to get the correct estimates.