An epidemic model on the dispersal networks at population and individual levels

Abstract

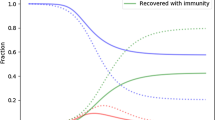
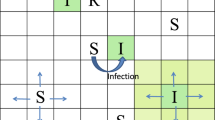
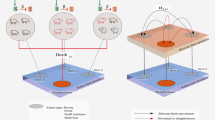
A network model at the population level and the individual level, which simulates both between-herd dynamics and within-herd dynamics, is formulated. We investigated effects of dispersal rates and local dynamics on the outcome of an epidemic at the population level. Numerical studies show that dispersal may strengthen spread of the disease on average, but lead to a less tendency for damped oscillation. Further, different types of clustering behaviors, from synchronized to completely desynchronized, are observed within our system. The results show that strengthening the coupling between farms via the immigration of infectives tends to enhance (in-phase) synchronization. Dynamic complexity, including chaotic, quasi-periodic or periodic behaviour, is observed in our model with varying the coupling strength. The main results help to explain differences in observed epidemiological patterns and to identify possible causes for different strains of Salmonella developing so much variation in their infection dynamics in UK dairy herds.

Appendices

Appendix 1

1.1 Matrices contributing to the disease-free equilibrium $E_0$

Define a matrix M(z)

$$\begin{aligned} M(z)=\left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} B_1(z)-d_1+h_Sa_{11} &{} h_Sa_{12} &{} \cdots &{} h_Sa_{1n}\\ h_Sa_{21}&{} B_2(z)-d_2+h_Sa_{22} &{} \cdots &{} h_Sa_{2n}\\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ h_Sa_{n1}&{} h_Sa_{n2} &{} \cdots &{} B_n(z)-d_n+h_Sa_{nn} \end{array}\right) . \end{aligned}$$

for any non-negative constant z. And matrix B gives

$$\begin{aligned} B=\left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} h_Sa_{11}+b_1-d_1 &{} h_Sa_{12} &{} \cdots &{} h_Sa_{1n}\\ h_Sa_{21}&{} h_Sa_{22}+b_2-d_2 &{} \cdots &{} h_Sa_{2n}\\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ h_Sa_{n1}&{} h_Sa_{n2} &{} \cdots &{} h_Sa_{nn}+b_n-d_n \end{array}\right) . \end{aligned}$$

1.2 Matrices contributing to the next generation matrix H

$$\begin{aligned} \begin{array}{rl} F_1&{}=\left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} \beta _1 S_1^*&{} 0 &{} \cdots &{} 0\\ 0 &{} \beta _2 S_2^* &{} \cdots &{} 0\\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ 0 &{}0 &{} \cdots &{} \beta _n S_n^* \end{array}\right) , \quad F_2=\left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c } \nu _1 S_1^* &{} 0&{} \cdots &{} 0\\ 0 &{} \nu _2 S_2^*&{} \cdots &{} 0 \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ 0 &{}0&{} \cdots &{} \nu _n S_n^* \\ \end{array}\right) , \\ V&{}=\left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} D_1-h_Ia_{11} &{} -h_Ia_{12} &{} \cdots &{} -h_Ia_{1n}\\ -h_Ia_{21}&{} D_2-h_Ia_{22} &{} \cdots &{} -h_Ia_{2n}\\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ -h_Ia_{n1}&{} -h_Ia_{n2} &{} \cdots &{} D_n-h_ia_{nn} \end{array}\right) .\end{array} \end{aligned}$$

where $D_i =d_i +\alpha _i +\gamma _i$, $i=1,\ldots , n$.

$$\begin{aligned} \varLambda =\left( \begin{array}{ c@{\quad }c@{\quad }c@{\quad }c} \lambda _1 &{} 0 &{}\cdots &{}0 \\ 0&{} \lambda _2 &{} \cdots &{}0 \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ 0&{}0&{}\cdots &{}\lambda _n \\ \end{array}\right) , \quad Q=\left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} \mu _1+\nu _1 S_1^* &{} 0 &{}\cdots &{}0\\ 0 &{} \mu _2+\nu _2 S_2^* &{} \cdots &{}0 \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ 0 &{}0 &{}0 &{} \mu _n+\nu _n S_n^*\\ \end{array}\right) , \end{aligned}$$

Appendix 2

The dispersal rates for the susceptibles, infectives and removeds are generated uniformly distributed to represent varying dispersal rates. In particular, we let $h_S=2^{-2} rand(10,1)$; $h_I= 2^{-2} rand(10,1); h_R= 2^{-2} rand(10,1)$. For Fig. 2b, the dispersal rates are $h_b=(h_S, h_I, h_R)^T$, and

$$\begin{aligned} h_b=\left( \begin{array}{ cccccccccc} 0.1038 &{} 0.0762 &{} 0.2186 &{} 0.0038 &{} 0.1920 &{} 0.2427 &{} 0.2475 &{} 0.1972 &{} 0.1097 &{} 0.1246 \\ 0.0535 &{} 0.1609 &{} 0.0800 &{} 0.2400 &{} 0.1817 &{} 0.1030 &{} 0.1861 &{} 0.0670 &{} 0.1100 &{} 0.2333 \\ 0.1708&{} 0.0531 &{} 0.2098 &{} 0.1572 &{} 0.0334 &{} 0.0518 &{} 0.1518 &{} 0.1575 &{} 0.0926 &{} 0.1438 \\ \end{array}\right) \end{aligned}$$

For Fig. 2c, the dispersal rates are $h_c=(h_S, h_I, h_R)^T$, and

$$\begin{aligned} h_c=\left( \begin{array}{ cccccccccc} 0.0303 &{} 0.1127 &{} 0.1790 &{} 0.2232 &{} 0.0683 &{} 0.0637 &{} 0.2164 &{} 0.0581 &{} 0.2012 &{} 0.2271 \\ 0.0580 &{} 0.0598 &{} 0.0124 &{} 0.0196 &{} 0.1602 &{} 0.0477 &{} 0.2110 &{} 0.0435 &{} 0.0427 &{} 0.2486 \\ 0.1099 &{} 0.0850 &{} 0.0786 &{} 0.0913 &{} 0.0983 &{} 0.1479 &{} 0.0299 &{} 0.0095 &{} 0.1146 &{} 0.2175\\ \end{array}\right) \end{aligned}$$