Spatial Interpolation of Gauge Measured Rainfall Using Compressed Sensing

Abstract

In this work, we suggest new spatial precipitation interpolation schemes using compressed sensing (CS), which is a new framework for signal acquisition and smart sensor design. Using CS, the precipitation maps are recovered in high resolution by obtaining sparse coefficients of radial basis functions(RBFs). Two types of methods are designed according to the construction methods of CS matrix. In the first type, the CS matrix is derived as the product of an m × n (n ≫ m) weights matrix of inverse distance weighting (IDW) and an n × n radial basis function (RBF) matrix. The second type of CS matrix consists of an m × n RBF matrix that depends on a few observation vectors and a number of n unknown vectors. The advantage of the proposed CS methods is that it can be represented at a high resolution because it is interpolated based on a large number of bases (or degrees of freedom). This prevents the variance value from being much smaller than the actual value due to interpolation using a few observation scales. To test our CS interpolation schemes, interpolation results were compared with IDW, Ordinary Kriging (OK) and RBF interpolation methods for analytic test function and some actual rainfall data. In the case of an analytic test function, when the proposed method is compared at high resolution, the error from the true value is the smallest. In real rainfall data, comparison with real values is not possible at high resolutions, but the error with the observed data is the smallest in terms of ‘spatial variogram’. In addition, the proposed CS method generates hight resolution data from rainfall cases, showing promising results when identifying peaks.

1 Introduction

Spatial precipitation interpolation plays an important role in flood control and water resource management. However, precipitation exhibits great spatial variability, making it difficult to estimate spatial precipitation. Maps of precipitation have a wide range of applications and many different interpolation procedures have been used to derive gridded rainfall field from sparsly scattered observation data. General approaches in mapping precipitation from sparse point data include regression analysis, inverse distance weighting (IDW), radial basis function (RBF), and geostatistical methods. Some studies show that performances of the methods have some differences among them. For instance, Goovaerts (2000) compared the interpolation techniques such as IDW, regression, Ordinary Kriging (OK), Simple Kriging with varying local means (SKlm), Kriging with an External Drift (KED), and ordinary co-Kriging (OCK) for annual and monthly precipitation in a region of Portugal. Lloyd (2005) compared monthly precipitation fields in Great Britain derived from Moving Window Regression (MWR), IDW, OK, SKlm, and KED. Kurtzman et al. (2009) tested different parametrization of IDW and a Local Weighted Regression (LWR) at hilly areas in the eastern Mediterranean using 16 years of daily data. Zhang and Srinivasan (2009) used Nearest Neighborhood (NN), IDW, Simple Kriging (SK), OK SKlm, and KED to interpolate ten years of daily spatial precipitation using 41 rain gauges in the downstream area of the Yellow River basin. These studies show none of the methods consistently outperforms. In addition, different methods result in similar area mean, but show significant different values of minimum and maximum precipitation, and coefficient of variation.

The two popular spatial interpolation methods are IDW and Kriging. IDW is one of the most widely used deterministic spatial interpolation models for fast and easy calculations. The weights of IDW for linear combination are only dependent on the distance between locations. Thus, IDW works well if the values at unobserved locations are expected to be similar to the values of the nearby locations.

Kriging is a geostatistical interpolation technique that considers both the distance and variation between known data points to estimate unknown values. Despite the popularity of IDW, this method requires preselection of the distance-decay parameter, and in comparison with Kriging, it is not possible to estimate the variance of the predicted values at unsampled locations (Lu and Wong 2008; Burrough and McDonnell 1998). Kriging is relatively cumbersome compared to IDW, but it is the preferred method for many spatial statistical analysis. It requires the extra steps to derive the empirical variogram and to fit a variogram function. For successful Kriging interpolation, it is important to identify the theoretical variation that best fits the given data (Sen and Sahin 2001).

RBF interpolation is an accurate interpolation method in which interpolated surfaces directly pass through observed data. In previous studies of Hardy (1971, 1990), it proved to be useful for hydrologic models. Palaseanu and Pearlastine (2008) found that the RBF model outperformed the IDW and spline interpolation methods, and Fujisaki et al. (2010) employed the RBF multiquadric method to interpolate water stage (depth) in the Everglades in Florida. Similar to IDW, the interpolated surface by RBF method is spatially smoothed due to the smoothness of the selected basis function. Disadvantages of the RBF method are that the linear matrix equation must be solved to find the interpolation coefficients and the accuracy of the interpolation results is highly dependent on the basis type or smoothing parameter.

Compressed sensing (CS) is a sparse signal processing technique for efficient acquisition, allowing the signal to be reconstructed by solving an underdetermined linear system. This technique works on the principle that through optimization, the signals can be recovered from much less samples than is normally required. In recent years, CS has attracted considerable attention in the areas of applied mathematics, such as biomedical (Donoho and Pauly 2007), astronomy (Bobin et al. 2008), and atmospheric science (Ozturk et al. 2014), due to the possibility to surpass the traditional limits of sampling theory. CS has been used to recover missing spatial or temporal data (Guo et al. 2011; Li and Parker 2008).

The purpose of this study is to present new spatial interpolation methods as alternatives to overcome the problem of spatial variability decrease duo to spatial smoothing in IDW or RBF. We propose two methods, which have large degree of freedom with underdetermined system. This systems are solved by l₁ minimizing CS algorithm. The proposed methods are compared with IDW, OK and RBF and demonstrated using an analytic 2-dimensional test function and several precipitation fields obtained from Automatic Weather Station (AWS) data. The rest of the paper is organized as follows. In Section 2, all used interpolation methods are introduced. The used data, process of quality control, and the used methods for assessing the performances are presented in Section 3. In Section 4, proposed CS interpolation schemes are applied and compared for both an analytic test function and real rainfall data. The conclusions are given in Section 5.

2 Methods

In this section, we briefly introduce IDW and RBF and propose two CS-based algorithms.

2.1 Inverse distance weighting (IDW) and ordinary Kriging (OK)

IDW method has been widely used in the literature and regarded as one of the standard spatial interpolation procedures because it is relatively fast and easy to interpret and compute. The method assumes that interpolating surface is more influenced by nearby locations rather than by farther locations. Two dimensional IDW scheme for a new unknown (interpolated) value $Z(s_{i}^{*})$ at a new location $s_{i}^{*}$ is given by

$$ Z(s_{i}^{*}) = \sum\limits_{k=1}^{m} w(r_{ik}) Z(s_{k}), \quad s_{i}^{*}, s_{k} \in \mathbb{R}^{2}, $$

(1)

where Z(s_k) is the observed values at locations s_k. The weight function is defined as $w(r_{ik})=\frac {\hat {w}(r_{ik})}{\sum \hat {w}(r_{ik})}$, where $\hat {w}(r_{ik})=1/r_{ik}^{\upbeta }$ and $r_{ik}=|s_{i}^{*}-s_{k}|$ (the distance between locations $s_{i}^{*}$ and s_k). Note that ${\sum }_{k=1}^{m} w(r_{ik})=1$. β is an important (distance-decay) parameter for IDW interpolation, and the optimal value β is dependent on the distribution of interest field.

In order to find the appropriate β, in advance, the (leave-one-out) cross-validation root mean square errors (CVEs) were computed for different β. Figure 1 shows the CVEs of IDW method for seven days’ rain data and an analytical test function for different β. The minimum CVEs for test function and for real precipitation events were observed near β = 5 and β = 3.5, respectively. In real precipitation data, the minimum CVE of IDW was observed at near β = 3.5, but the variation in CVEs was very small in the range β ∈ [3,5] and the variogram error for IDW was the smallest near β = 5. Therefore, in this work, we used β = 5 for analytic test function and actual precipitation data.

Fig. 1

CVEs of analytical test function and daily averaged CVEs of seven days’ data according to different β

OK is a classical method of Kriging that assumes constant unknown mean only over the neighborhood of nuknown position s_j. In this study, we used the ‘stable’ mode of OK which uses the following stable covariance function in Wackernagel (1995) to fit the experimental semivariogram (5) defined in Section 3.4,

$$ C (r_{ik}) = b \exp(-\frac{r^{\rho}_{ik}}{a}),$$

where b is the value at the origin, a the range parameter, ρ = 1.5, and r_ik = |s_i − s_j|.

2.2 Radial basis function (RBF) interpolation

In this paper, we consider two RBF interpolation methods using inverse multi quadric RBF (hereafter RBF-IMQ) and inverse quadratic RBF (hereafter RBF-IQ). The RBF interpolation in $\mathbb {R}^{2}$ has the form

$$ Z(s) = \sum\limits_{k=1}^{m} c_{k} \phi(r_{k}(s)), \quad s, s_{k} \in \mathbb{R}^{2}, $$

(2)

where ϕ(r_k(s)) is a radial basis function at the center (or observed position) s_k and r_k(s) = |s − s_k|. The point s is called the hidden or predicted position. In general RBF method, when $\{s_{k}\}_{k=1}^{m}$ is a set of distinct point in $\mathbb {R}^{2}$, if the hidden points are chosen as $\{s_{k}\}_{k=1}^{m}$ in Eq. 2, then Φ_{i, j} = ϕ(|s_i − s_j|) is an m × m nonsingular matrix and the following linear equation is uniquely solvable (Powell 1990).

$$ \left[\begin{array}{ccc} {\Phi}_{i,j} \end{array}\right]_{m \times m} \left[\begin{array}{ccc} c_{j} \end{array}\right]_{m \times 1} = \left[\begin{array}{ccc} Z(s_{i}) \end{array}\right]_{m \times 1}. $$

(3)

If $\{s_{i}^{*} \}_{i=1}^{n}$ is the grid points to be predicted, then the interpolated values $Z^{*}=\{Z(s_{i}^{*} )\}_{i=1}^{n}$ can be computed using the coefficients $\{c_{k}\}_{k=1}^{m}$ of Eq. 3 as

$$ \left[\begin{array}{ccc} Z^{*} \end{array}\right]_{n \times 1} = \left[\begin{array}{ccc} \phi(s_{i}^{*} -s_{k}) \end{array}\right]_{n \times m} \left[\begin{array}{ccc} c_{k} \end{array}\right]_{m \times 1}. $$

In this study, we have chosen the inverse multiquadric type of radial functions introduced by Hardy (1971, 1990) such that

$$ \phi(r_{k}(s))=(\lambda^{2} + r_{k}(s)^{2})^{-\alpha}, \quad \alpha > 0, $$

(4)

where r_k(s) is the distance between an unknown point s and an observed point s_k such that r_k(s) = |s − s_k|, and λ is the shape or smoothing parameter. If λ is large, then the shape of the basis is flat, while decreasing λ leads to a more peaked (or localized) basis function. We chose α = 1/2, the original inverse multiquadric (IMQ) introduced by Hardy (1971), and α = 1, referred to as the inverse quadratic (IQ) in Fornberg and Wright (2004). We also used the fixed shape parameter, λ = 1.

2.3 Compressed sensing (CS)

CS is achieved by solving the following optimization problem: ${\min \limits } \|\textbf {c}\|_{1}$ subject to Fc = Z, where $Z \in \mathbb {R}^{m}$, F is an m × n CS reconstruction matrix, and c is a n × 1 sparse vector (i.e., most of the components of c are zero), $\| \textbf {c}\|_{1} ={\sum }_{i=1}^{n} |c_{i}|$ is the discrete l₁ norm of the vector c. The problem can be described as the reconstruction of the sparse vector $\textbf {c} \in \mathbb {R}^{n}$ from the measurements of Z. The CS theory ensures that the number of components of c (the unknown signal) is much larger than the number of measurements (or observations) for reconstruction, i.e., n ≫ m.

The necessary conditions for the possible recovery of the original signal from compressed data were given in Candés et al. (2006a). The first condition is sparsity, where the signal has to be sparse in some domain. The second is incoherence, which is applied through the isometric property and is sufficient for sparse signals. In this study, to ensure the restricted isometry property (Candés et al. 2006a, 2006b), F is normalized by dividing elements in each column by the l₂ norm of that column such that $\hat {F}_{i,j} =F_{i,j}/L_{j}$, where $L_{j} = \sqrt {{\sum }_{i} (F_{i,j})^{2}}$. That is $\hat {F} \hat {\textbf {c}} =Y$. After normalization, the solution $\hat {\textbf {c}}$ was computed via a standard CS algorithm in Candés and Romberg (2005). Then, the coefficients c were obtained by $\textbf {c}_{j} = \hat {\textbf {c}}_{j}/L_{j}$.

2.3.1 Type 1: Compressed Sensing Matrix Obtained from IDW and RBF: CS(I)

In conventional signal processing, the reconstruction image $Z_{n \times 1}^{*}$ can be obtained by solving Fc = Z, where F = WΦ. W is an m × n measurement matrix, and Φ is an n × n basis matrix such that Z^∗ = Φc. One of the most important ideas for constructing the compressed sensing problem is to find an appropriate basis to express Z^∗. In this paper, we have chosen an RBF as a basis for Z^∗.

Let $\{Z(s_{k})\}_{k=1}^{m}$ be observed value at location $\{s_{k}\}_{k=1}^{m}$, and $\{ Z(s_{i}^{*}) \}_{i=1}^{n}$ be unobserved value at location $\{s_{i}^{*}\}_{i=1}^{n}$. The sensing reconstruction matrix F = WΦ can be designed by combining IDW and RBF schemes such that

$$\left[\begin{array}{ccc} w(|s_{1} -s_{1}^{*} |) & {\ldots} & w(|s_{1} -s_{n}^{*} |)\\ {\vdots} & & {\vdots} \\ w(|s_{m} -s_{1}^{*} |) & {\ldots} & w(|s_{m} -s_{n}^{*} |) \end{array}\right] \left[\begin{array}{ccc} \phi(|s_{1}^{*} -s_{1}^{*} |) & {\ldots} & \phi(|s_{1}^{*}-s_{n}^{*} |)\\ {\vdots} & & {\vdots} \\ \phi(|s_{n}^{*} -s_{1}^{*} |) & {\ldots} & \phi(|s_{n}^{*}-s_{n}^{*} |) \end{array}\right] \left[\begin{array}{ccc} c_{1}\\ \vdots\\ c_{n} \end{array}\right] $$

$$ = \left[\begin{array}{ccc} Z(s_{1}) \\ {\vdots} \\ Z(s_{m}) \end{array}\right] $$

$$ \Leftrightarrow W_{m \times n} {\Phi}_{n \times n} \textbf{c}_{n \times 1} = Z_{m \times 1}, $$

where w(r) is the IDW weight function and ϕ(r) is the radial basis function. Since the reconstruction matrix F = WΦ is m × n (n ≫ m), the system is underdetermined. The solution c is obtained by the standard CS algorithm in Candés and Romberg (2005). Then, the large number of unobserved values $\{ Z(s_{i}^{*}) \}_{i=1}^{n}$ at $\{ s_{i}^{*} \}_{i=1}^{n}$ are easily calculated by multiplying Φ by c, such that Z^∗ = Φc.

2.3.2 Type 2: Compressed Sensing Matrix Obtained from RBF: CS(II)

Analogous to Type 1, we design the CS system Fc = Z by substituting the data $\{s_{k} \}_{k=1}^{m}$ and $\{ s_{i}^{*} \}_{i=1}^{n}$ (n ≫ m) into Eq. 2 such that

$$ Z(s_{k})=\sum\limits_{i=1}^{n} c_{i} \phi (|s_{k}-s_{i}^{*} |), \quad k=1,\ldots, m, $$

so that the CS reconstruction matrix F is composed of just an RBF matrix dependent on observation vectors $\{s_{k}\}_{k=1}^{m}$ and the large number of unknown vectors $\{ s_{i}^{*} \}_{i=1}^{n}$ such that

$$ \begin{array}{@{}rcl@{}} &&~~\left[\begin{array}{ccccc} \phi(|s_{1} -s_{1}^{*} |) & \phi(|s_{1} -s_{2}^{*} |) & {\ldots} & \phi(|s_{1} -s_{n}^{*} |)\\ {\vdots} & {\vdots} & & {\vdots} \\ \phi(|s_{m} -s_{1}^{*} |) & \phi(|s_{m}-s_{2}^{*} |) & {\ldots} & \phi(|s_{m} -s_{n}^{*} |) \end{array}\right] \left[\begin{array}{cccccc} c_{1}\\ \vdots\\ c_{n} \end{array}\right]\\ &&= \left[\begin{array}{ccc} Z(s_{1})\\ \vdots\\ Z(s_{m}) \end{array}\right] \end{array} $$

$$ \Leftrightarrow F_{m \times n} \textbf{c}_{n \times 1} = Z_{m \times 1}. $$

Similar to the Type 1 scheme, after solving the underdetermined linear system Fc = Z, the unknown values $\{ Z(s_{i}^{*}) \}_{i=1}^{n}$ at $\{ s_{i}^{*} \}_{i=1}^{n}$ can be obtained by Z^∗ = Φc, where Φ is the same basis transform matrix composed of the RBF defined in Type 1.

3 Data Setup and Evaluation Method

3.1 Study Area

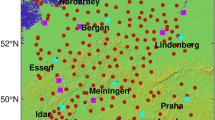
In this study, we used the rainfall intensity data measured from tipping-bucket rain gauges with 0.5 mm resolution in 325 Automatic Weather Stations (AWSs) observations within the selected domain (see Fig. 2) in the summer of 2012. This area is the western coastal area including the capital city of the Republic of Korea and covers an area of 200 km × 300 km. In Fig. 2, some areas (i), (ii), and (iii) were selected to compare the interpolated images of all methods. Zone (i) is a region with few AWSs, (ii) almost half of the zones have AWS installed, and (iii) zone is an edge zone, although AWSs are moderately distributed.

Fig. 2

Automatic weather stations (325 total) within the area 125.65E–127.98E and 34.95N–37.72N in the 200 km × 300 km domain (left), and 295 AWSs and 225 AWSs in the reference domain (right)

3.2 Data Quality Control

One minute rainfall data from AWSs was filtered by the quality control (QC) procedure consisting of integrity check, climatological extreme-value check, and spatial consistency check. In the integrity check, AWSs are excluded when the accumulated rainfall decreases as increasing accumulation time or when the missing rate of daily rainfall of AWS is greater than the empirical value 12.5 %. AWSs with one minute rainfall greater than 8 mm (corresponding to 480 mm/h) were also eliminated based on the climatological extreme-value for the summer season in Korea. For the spatial consistency check, spatial consistency index (SCI) is used to identify outliers of the rainfall measured from the neighboring AWSs (Kondragunta 2001) as follows:

$$ \begin{array}{@{}rcl@{}} SCI &=&\frac{|R_{i}-Q_{50}|}{Q_{75}-Q_{50}} ~\text{if} ~ Q_{75}\neq Q_{25} \quad \text{otherwise,}\\ SCI &=& \frac{|R_{i} - Q_{50} |}{MAD}, \end{array} $$

where R_i indicates the rainfall intensity (mm/h) at i^th AWS, and Q₅₀, Q₂₅, and Q₇₅ represent the median (50^th), 25^th and 75^th percentile of the rainfall within a given range threshold from the selected i^th AWS. MAD is a mean absolute deviation and calculated as follows:

$$ MAD = \frac{1}{N} \sum\limits_{i=1}^{N} | R_{i}-Q_{50} |, $$

where N is the total number of AWSs within the given range threshold from the each AWS. To calculate SCI, the range threshold is fixed at 30 km and the SCI is set to zero if MAD is zero. The 1-minute rainfall of AWS is flagged as an outlier when the SCI of AWS is greater than the predefined threshold (= 3.0). In the case of AWS rainfall being affected by intense thunderstorms, the consistency with the neighboring rainfall values does not have to be high. Thus, to avoid the incorrect elimination, AWSs were removed when the number of outlier flag is greater than the predefined threshold that was empirically set to 25 % in this study. Note that these thresholds used in this study are empirical values considering Korea’s climate, and currently the Korea Meteorological Agency is also using the same thresholds for QC processing in AWS.

3.3 Data Structure

Note that the number of AWSs varies from case to case after the data QC process. We denote the number of AWSs as n after applying QC process in each event. Overlapping observation locations are not permitted the linear system of the RBF method to ensure the uniqueness of the solution. In addition, it is necessary to keep more than a certain distance between locations in order to construct stable RBF matrix. Thus, in this study, we used AWSs that are more than 6 km apart among n AWSs, and the number of these AWSs actually used in the analysis is denoted by n₀. Figure 2 shows the study area (left) and the locations of 295 (= n) AWSs and 225 (= n₀) AWSs (right) at the domain 200 × 300 km² on June 30, 2012.

3.4 Evaluation methods

All computations are considered in the scaled reference domain [0,20] × [0,30]. To evaluate the performance of presented interpolation method, we used root mean square error (RMSE) or CVE. Also, to check the spatial statistical error, the spatial variogram γ(r) is computed. Since the theoretical variogram is related to the variance of the values such that 2γ(x, y) = var(Z(x) − Z(y)), the the following experimental semivariogram $\hat {\gamma } (r)$ was used.

$$ \hat{\gamma}(r) = \frac{1}{N(r)}\sum\limits_{r} \left( Z(s_{i})-Z(s_{j})\right)^{2}, $$

(5)

where Z(s_i) is the observed rainfall at s_i and N(r) is the number of pairs (s_i,s_j) such that |s_i − s_j| = r. For numerical computation, N(r) is defined as the number of pairs (s_i,s_j) such that r ≤|s_i − s_j| < r + h, and h = 0.5 (5 km).

4 Results

4.1 Tests for an Analytic Function

4.1.1 Analytic function

Before analyzing the real rainfall data, we tested our interpolation methods using an analytic test function with 225 AWS points (= n₀ on June 30) defined in the reference domain [0,20] × [0,30] such that

$$ \begin{array}{@{}rcl@{}} f(x,y) \!\!&=&\!\! 20 e^{-\frac{1}{3}(0.7(x-10))^{2}-\frac{1}{10}(0.6(y-7))^{2}} +5e^{-\frac{1}{4}(x-10)^{2}-\frac{1}{2}(0.7(y-15))^{2}} \\ &+&\!\! 8e^{-\frac{1}{6}(0.4(x-10))^{2}-\frac{1}{10}(y-5)^{2}} 10e^{-\frac{1}{5}(0.6(x-18))^{2}-\frac{1}{10}(0.9(y-30))^{2}} \\ &+&\!\! 35e^{-\frac{1}{2}(x-15)^{2}-\frac{1}{6}(0.8(y-25))^{2}}. \end{array} $$

(6)

To determine an analytic test function, we modified Franke’s function in Franke (1982) which is a standard test function for 2D scattered data fitting. The shape of f(x, y) is shown in Fig. 3a. Using the test function f(x, y), each interpolation technique was employed in the reference domain [0,20] × [0,30] using 225 AWS points. Then, the interpolated values were compared with the exact f(x, y) on 40 × 60 = 2400 uniform grids (5 km resolution).

Fig. 3

Interpolated images with 5 km resolution. For interpolation, 225 AWS points were used for the test function. The CS reconstruction matrix size is 225 × 2400

4.1.2 Interpolated images

Interpolated images of the test function f(x, y) using 225 points in Fig. 2 are presented in Fig. 3b-i. Overall, in the region where a sufficient number of AWSs are distributed, the interpolation result appears to coincide with the function f(x, y). On the other hand, in the regions (i) and (ii) in Fig. 3a with few AWSs, a clear difference is appeared in the interpolated results according to the interpolation methods. CS methods appropriately recover the field in region (ii) and only CS-IQ interpolates no precipitation (see Fig. 3h and i) in the region (i) where f(x, y) are all 0. Interestingly, CS-IQ produces strong precipitation in region (ii), and RBF and OK methods produce weak precipitation in the region (iii) where f(x, y) = 0 are all 0.

4.1.3 Quantitative evaluation

Table 1 shows the quantitative errors, such as RMSEs, mean, varience and RMSE of variogram. Note that, without CVEs, all values are obtained from 2400 uniform grid points. In this case, CS(II)-IMQ have the best results in terms of RMSE and CVE computed at 225 AWSs. All methods except IDW, OK, and CS(II)-IQ have negative mean biases and IDW and CS(II)-IQ have the best mean bais values. Interestingly, RBF, OK and IDW do not exceed the actual maximum value, but for CS methods, they have maximum values that are slightly larger than the actual value. Increasing the maximum value of the predicted value also can affect the variance value. In Table 1, the variances of CS-IMQs are not so small than the actual variance compared to IDW and RBF, but rather the variances of CS-IQs are slightly larger than the actual values. This is probably because the CS methods have greater degrees of freedom than other methods.

Table 1 Comparisons of interpolation accuracies of four methods

The rainy region (f(x, y) ≥ 0.1 mmh^− 1) of analytic function is 75 % in the reference domain. However, IDW, OK, RBF-IMQ, and RBF-IQ have rainy region areas of 81 %, 92 %, 88 %, and 89 %, respectively. This indicates that the methods generate significant false alarm rainfall.’ In particular, in the case of RBF, the mean bias in Table 1 is negative, so it is underestimated overall. CS-IMQ also has a 4 % false alarm rainfall area, which is relatively smaller than IDW (13 %), OK (17 %), or RBF (14 %). CS-IQ methods result in 71 % and 72 % rainfall areas, respectively.

As a result, the common interpolation methods generally render rainfall field oversmooth due to the sparse sampling points. Thus, the variance or the maximum value is calculated to be smaller than true value. On the other hands, the CS interpolation techniques can be useful for finding peak values in some areas due to the high degree of freedom of basis.

4.1.4 Spatial variograms

Figure 4 displays the experimental variograms of the interpolated values at 2400 points. The CS(I)-IMQ model has the best fit and the smallest error between exact variogram and interpolation as RMSE = 1.41 mmh^− 1. CS(II)-IMQ is the second best match with RMSE = 2.59 mmh^− 1. The variogram generated by RBF-IQ is significantly different from the actual value of f(x, y). This result is consistent with the errors between variances of Table 1.

Fig. 4

Variogram functions γ(r) obtained from the analytic test function f(x, y) using 2400 points. The other variogram function is computed using 2400 interpolated points approximated from 225 AWS points

For this analytic test function, it is certain that the proposed CS interpolation techniques show superior results in that the shape and peak are well produced compared to RBF or IDW interpolation. The shape and accuracy of the CS methods were not much dependent on the CS type (I or II), but influenced by the type of basis such as IMQ and IQ.

4.2 Real Rainfall Data

4.2.1 Selected events set

Table 2 shows the characteristics of the selected events in 2012. For each event, some descriptive statistics were calculated. In Table 2, n is the number of AWSs after QC in each event, and n₀ is the number of used AWSs for interpolations. The notations σ(R) and E(R) represent the standard deviation and averge vlaue of the rain rate R, respectively. One day’s set has 24 hours data set and each hour set has n₀ AWS values. Thus, in this table, E_t(σ_s(R)) is sptial standard deviation of R for n₀ AWSs, and average of σ_s(R) for 24 hours. Similarly, σ_t(E_s(R)) represents the average of n₀ rain rates R and then the stnadard devivation of E_s(R) for 24 hours. The ${\max \limits } (\sigma _{s}(R))$ is the maximum value of σ_s(R) for 24 hours. The average daily rainfall intensity had the highest temporal/spatial variability on July 6 and the average rainfall intensity was 4.2 mmh^− 1. The day with the lowest temporal/spatial variation was on July 14, and the daily mean rainfall intensity was 1.0 mmh^− 1.

Table 2 Statistics of rainfall events

4.2.2 Interpolated images

In the analysis for real rainfall data, CS reconstruction matrix F with the size n₀ × 3750 (= 50 × 75) is used to generate rainfall field at 4 km resolution. Interpolated rain intensity images using 225 points at 02:00 LST on June 30 are presented in Fig. 5. Similar to the results in Section 4.1.2, the rain fields are interpolated differently in the area with a small number of AWSs in the (i) and (ii) areas in Fig. 5a. Also, it is shown that the CS method using IQ has a tendency to identify some peaks in the rain field.

Fig. 5

Interpolated rain intensity images on 50 × 75 grids (4 km resolution) using values from 225 AWSs. The time is 0200 LST, June 30, 2012

4.2.3 Quantitative evaluation

In the analytic test function in Section 4.1, quantitative evaluations were performed at 2400 grid points with a 5 km resolution. On the other hand, in real AWS rainfall data, since the exact values are not known at grid points, only CVEs were calculated at the AWS points. The daily (24 hours) average CVEs are presented in Table 3. Interestingly, for real rainfall data, the CS methods did not yield the best CVEs, unlike the results of the analytic test function. In CVEs, there is no significant difference in the overall error, but with a slight difference, RBF-IMQ interpolation yields the smallest error of 1.89 mm h^− 1 among all methods and the following is OK interpolation with 1.92 mm h^− 1. RBF-IQ is 1.93 mmh^− 1 and IDW is 2.01 mmh^− 1. The CS methods have the largest CVEs, of which the CS(II)-IMQ is the smallest with a value of 2.02 mmh^− 1 and the CS(I)-IQ is the largest with a value of 2.06 mmh^− 1.

Table 3 Comparison of leave-one-out cross-validation RMSE (CVE) for each method

In this study, we applied the interpolation methods to n₀ AWSs that are more than 6 km from each other among the n AWSs for the stability of the RBF matrix. Thus, it is possible to compare the predicted value with the actual value at the remaining n − n₀ points that are not used in the interpolation method. The RMSE of the differences between prediction value and actual AWS rain rate is computed in Table 4. Overall, the errors are similar to each other, but OK interpolation RMSE is the smallest as 1.49 mmh^− 1 and the RBF-IQ was the next lowest at 1.52 mmh^− 1. The CS methods have smaller RMSEs than IDW of 1.64 mmh^− 1. CS(II)-IQ was 1.60 mmh^− 1 the lowest among CS methods.

Table 4 Daily averaged RMSEs for n − n₀ AWSs

4.2.4 Some discussion on the accuracy of the CS methods for real rainfall data

For real rainfall data, the daily mean CVEs were slightly larger than other interpolation methods, as opposed to the results of the analytic test function. Figure 6 uses box plots to show the all CV errors according to different rain rate. In this figure, the numbers above the boxes represent the mean and median, respectively, from above. Interestingly, in Fig. 6a, the largest error corresponding to the outlier occurred at weak rain rate of AWS. That day was the time with the highest average rainfall intensity and the largest spatial variation. In Fig. 6a, the CS-IQ methods have the narrowest interquartile range (IQR) values, while they contain the largest outlier. At rain rates above 5 mmh^− 1, the IQRs of CS methods were slightly increased than that of RBF, but the median and mean values show the closest values to zero. In particular, the values in RBF are the largest when the rainfall intensity is larger. As a result, using the CS methods improves the bias value, but may increase the range of predicted values, resulting in higher CVEs.

Fig. 6

Cross-validation (CV) errors for different rain rates: a 0 ≤ R < 5 mmh^− 1 b 5 ≤ R < 10 mmh^− 1 c10 ≤ R < 15 mmh^− 1 d15 ≤ R < 20 mmh^− 1 e 20 ≤ R < 25 mmh^− 1 (r) 25 ≤ R < 30 mmh^− 1. The numbers above the box plots represent mean (above) and median (bottom) of CV errors

Figure 7a shows the location and value of the removed AWS when the largest CV vlaue was obtained by the CS methods in Fig. 6. Figure 7b-d shows the fields interpolated by RBF-IMQ, CS(I)-IQ, and CS(II)-IQ, except for the AWS value in the circle, respectively. As expected, the two-dimensional rainfall field of RBF is smoothed, whereas the CS methods yield better minimum and maximum values. In particular, when another point on the west side of the lack of AWSs is eliminated in Fig. 7e, the western part is smoothed, resulting wide areas of light rainfall (see Fig. 7f).

Fig. 7

a The locations of AWS where the largest CV error is observed in the CS methods. The prediction fields by b RBF-IMQ, c CS(I)-IQ, and d CS(II)-IQ after excluding the point. The region of the circle represents the AWS that is excluded from interpolations. On the same day, prediction fields by f RBF-IMQ, g CS(I)-IQ, and h CS(II)-IQ after excluding one more AWS in the wertern region

While conventional interpolation methods do not properly predict minima and maxima, more extreme values can be produced in CS due to the high degree of freedom. This property of CS may be a factor in making CVEs higher than other interpolation methods. In addition, the quality of observations can be a significant factor affecting the error in interpolations. In particular, the data quality issue may have a more severe impact on the CVE of CS methods than other interpolation methods, due to the nature of CS methods for reconstructing the proper spatial structure.

4.2.5 Spatial variogram

Table 5 reports the variogram RMSEs at each time from 1:00 to 10:00 (LST) on June 30, 2012, indicating all CS methods have smaller errors than OK, IDW or RBF. The daily averaged variogram errors over 7 days are shown in Table 6. The mean over 7 days also had the lowest error of the CS method, and the highest variogram error in the RBF methods. Figure 8 shows the experimental variograms of the interpolated fields with n₀ = 225 AWSs at 1:00 (left) and 10 hours averge values during 1:00 - 10:00 on June 30. All CS methods show much smaller variogram errors than IDW or RBF.

Table 5 Variogram errors on June 30, 2012

Table 6 Daily averaged RMSEs between variograms on n₀ points and predicted 3750 points

Fig. 8

Experimental variogram graph of rain rates (blue line) at 225 AWSs, and variogram graphs of the values interpolated at 3750 points using 225 AWSs

5 Conclusions

A new spatial interpolation method of precipitation field using CS technique was proposed. CS is a signal processing technique for efficiently obtaining and reconstructing a signal, by finding solution for the under-determined linear system. The most important aspect of the CS technique is to construct a CS matrix, which is mainly composed of the product of an appropriate measurement matrix and a basis matrix. The matrix was constructed using IDW and RBF (Type 1) or RBF (Type 2). Their performance was verified by using an analytic test function and observed rainfall data from automatic weather station and was compared with the conventional spatial interpolation methods such as IDW, RBF, and OK.

The new methods (Type 1 & 2) outperformed the conventional methods in the analytic test function. In particular, they fit the analytic test function better and had smaller errors in terms of the variogram. The new methods also showed the closest variogram for the observed rainfall data but slightly worse performance in RMSE. The conventional RBF with the Hardy’s inverse multiquadric function performed the best in RMSE. This result is attributed from the smoothed field by the conventional methods. However, the new method is far superior in reconstructing the spatial structure of rain field.

The shape of the interpolated rain field and the accuracy of the new methods were strongly dependent not on the CS type (either Type 1 or 2) but on the type of basis. In general, the conventional IDW and RBF had a tendency to estimate the wide rainy areas and, moreover, made the smooth rainfall field using a small number of observed data to obtain higher accuracy. However, the new methods did not flatten the field even though they used the same smoothing parameter as the conventional RBF and IDW. The new methods were also suitable for detecting peaks, which would be useful for identifying extreme values (heavy rainy area) in sparse rain data.

The new method improves the bias but increases the CVE due to the wide prediction range. This seems to be related to the CS’s high degree of freedom. In addition, when using RBF or IDW, the optimal distance or shape variable were used. However, the optimality of these variables in CS remains to be explored. An appropriate CS matrix is one of the most important issues in CS optimization. The product of IDW and RBF matrix or a modified RBF matrix is used as a CS matrix in this study. The general number of basis for common interpolation methods is less than or equal to the number of sample points. However, the CS method allows for more basis (degree of freedom), so that the CS method can be an effective method for spatial interpolation using a small number of data. Better results will be likely produced if the algorithm can be improved by finding another efficient CS matrix.