Multivariable control of a grid-connected wind energy conversion system with power quality enhancement

Abstract

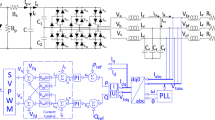
This paper proposes the design of a multivariable robust control strategy for a variable-speed WECS based on a SCIG. Optimal speed control of the SCIG is achieved by a conventional PI controller combined with a MPPT strategy. DTC-SVM technique based on a simple Clarke transformation is used to control the generator-side three-level converter in the variable speed WECS. The flow of real and reactive power between the inverter and the grid is controlled via the grid real and reactive currents and the DC link voltage using multivariable H$_{\infty }$control. The overall WECS and control scheme are developed in Matlab/Simulink and the performance of the proposed control strategy is evaluated via a set of simulation scenarios replicating various operating conditions of the WECS such as variable wind speed and asymmetric single grid faults. The power quality of the WECS system under H$_{\infty }$control control approach is assessed and the results show a significant improvement in the total harmonic distorsion as compared to that achieved with a classical PI control.

Appendices

Appendix A: Model of the grid-side

Figure 30 shows the grid-side inverter with DC source. To achieve bidirectional current flow through the converter, every switch is accompanied by an antiparallel diode. The switched converter in normal operation produces current through neuter point N, for different characteristics, depending on the operating conditions. This current flow creates an unbalance (charge and discharge of the DC side of capacitors) in the DC voltage to every capacitance capacitor $C_{dc}$. Usually with a finite value capacitors, the converter requires a special modulation algorithm that achieves a balanced DC side voltage [31].

This model is based on following simplifying assumptions [32–36]:

• All switches are supposed ideal.

• The three alternative source of voltages are balanced.

• The harmonics due the opening and closing actions of the switches are negligible.

• All voltage dips on the source side of inverter are represented by the resistor ${R}_{f}$.

• The currents and voltages in the capacitors are equal.

Using matrix representation, the three-phase abc system model of the network grid side is given by the following system of equations:

$$\begin{aligned} \frac{d}{dt}\left[ {{\begin{array}{l} {i_a } \\ {i_b } \\ {i_c } \\ \end{array} }} \right] =\left[ {{\begin{array}{l@{\quad }l@{\quad }l} {\frac{R_f }{L_f }}&{} 0&{} 0 \\ 0&{} {\frac{R_f }{L_f }}&{} 0 \\ 0&{} 0&{} {\frac{R_f }{L_f }} \\ \end{array} }} \right] \left[ {{\begin{array}{l} {i_a } \\ {i_b } \\ {i_c } \\ \end{array} }} \right] +\frac{1}{L_f }\left[ {{\begin{array}{l} {v_a -v_{oa} } \\ {v_b -b_{ob} } \\ {v_c -v_{oc} } \\ \end{array} }} \right] \end{aligned}$$

(32)

From the second hypothesis, the voltages of the three-phase source are:

$$\begin{aligned} v_{abc} =\left[ {{\begin{array}{l} {v_a } \\ {v_b } \\ {v_c } \\ \end{array} }} \right] =\sqrt{\frac{2}{3}}V_s \left[ {{\begin{array}{l} {\sin \left( {\omega _e t+\delta } \right) } \\ {\sin \left( {\omega _e t-\frac{2\pi }{3}+\delta } \right) } \\ {\sin \left( {\omega _e t+\frac{2\pi }{3}+\delta } \right) } \\ \end{array} }} \right] \end{aligned}$$

(33)

where $V_s$ is the efficient phase voltage of the source. $\delta$ is the phase angle between the fundamental voltages of the source and the inverter output voltages.

The Park transformation of Eq. (33) is given by:

$$\begin{aligned} v_{q,d,o} =V_s \left[ {{\begin{array}{l} {-\sin \delta } \\ {\cos \delta } \\ 0 \\ \end{array} }} \right] \end{aligned}$$

(34)

The system is balanced, so the homopolar part is zero. The model becomes:

$$\begin{aligned} \left[ {{\begin{array}{l} {v_q } \\ {v_d } \\ \end{array} }} \right] =\left[ {{\begin{array}{ll} {R_f }&{} {\omega _e L_f } \\ {-\omega _e L_f }&{} {R_f } \\ \end{array} }} \right] \left[ {{\begin{array}{l} {i_q } \\ {i_d } \\ \end{array} }} \right] +L_f \frac{d}{dt}\left[ {{\begin{array}{l} {i_q } \\ {i_d } \\ \end{array} }} \right] +\left[ {{\begin{array}{l} {v_{oq} } \\ {v_{od} } \\ \end{array} }} \right] \end{aligned}$$

(35)

From Eq. (35), the model of the source-side currents is given by:

$$\begin{aligned} \frac{d}{dt}\left[ {{\begin{array}{l} {i_q } \\ {i_d } \\ \end{array} }} \right] =\left[ {{\begin{array}{ll} {-\frac{R_f }{L_f }}&{} {-\omega _e } \\ {\omega _e }&{} {-\frac{R_f }{L_f }} \\ \end{array} }} \right] \left[ {{\begin{array}{l} {i_q } \\ {i_d } \\ \end{array} }} \right] +\frac{1}{L_f }\left[ {{\begin{array}{l} {v_q -v_{oq} } \\ {v_d -v_{od} } \\ \end{array} }} \right] \end{aligned}$$

(36)

From the third hypothesis can be defined the pulse functions as follows:

$$\begin{aligned} S_{abc} =\left[ {{\begin{array}{l} {S_a } \\ {S_b } \\ {S_c } \\ \end{array} }} \right] =\sqrt{\frac{2}{3}}D\left[ {{\begin{array}{l} {sin\left( {\omega _e t} \right) } \\ {sin\left( {\omega _e t-\frac{2\pi }{3}} \right) } \\ {sin\left( {\omega _e t+\frac{2\pi }{3}} \right) } \\ \end{array} }} \right] \end{aligned}$$

(37)

where $S_a ,S_b ,S_c$ are the equivalent switches respectively for phase “a”: $S_{a1}$ and $S_{a2}$, phase B: $S_{b1}$ and $S_{b2}$ and phase C: $S_{c1}$ and $S_{c2}$.

The voltages supplied by the inverter, considering only the fundamental component of the voltage (i.e. in the absence of harmonics), are expressed in terms of the DC link voltage and the switching functions as:

$$\begin{aligned} v_{oabc} =\left[ {{\begin{array}{l} {v_{oa} } \\ {v_{ob} } \\ {v_{oc} } \\ \end{array} }} \right] =\left[ {{\begin{array}{l} {S_a } \\ {S_b } \\ {S_c } \\ \end{array} }} \right] v_{dc} \end{aligned}$$

(38)

Since the system is balanced, the Park transformation of equation (38) is written as:

$$\begin{aligned} v_{oqd} =\left[ {{\begin{array}{l} {v_{oq} } \\ {v_{od} } \\ \end{array} }} \right] =Dv_{dc} \left[ {{\begin{array}{l} 0 \\ 1 \\ \end{array} }} \right] \end{aligned}$$

(39)

where D is the inverter conversion ratio between the fundamental of the output voltage and the DC voltage [37]:

$$\begin{aligned} D=\frac{\sqrt{v_{od}^2 +v_{oq}^2 }}{v_{dc} } \end{aligned}$$

(40)

The magnitude MI is given by:

$$\begin{aligned} MI=\frac{v_{o,\hbox {max}} }{v_{dc} }=\sqrt{\frac{2}{3}}D \end{aligned}$$

(41)

Substituting (34) and (39) into (36) gives:

$$\begin{aligned} \frac{d}{dt}\left[ {{\begin{array}{l} {i_q } \\ {i_d } \\ \end{array} }} \right] =\left[ {{\begin{array}{ll} {-\frac{R_f }{L_f }}&{} {-\omega _e } \\ {\omega _e }&{} {-\frac{R_f }{L_f }} \\ \end{array} }} \right] \left[ {{\begin{array}{l} {i_q } \\ {i_d } \\ \end{array} }} \right] +\frac{1}{L_f }\left[ {{\begin{array}{l} {-V_s \sin \delta } \\ {V_s \cos \delta +Dv_{dc} } \\ \end{array} }} \right] \end{aligned}$$

(42)

Based on the previous assumptions, the DC link current is:

$$\begin{aligned} i_{dc1} +i_{dc2} =2i_{dc} =S^{T}i_{abc} \end{aligned}$$

(43)

In the (d, q) axes:

$$\begin{aligned} 2i_{dc} =S^{T}M_p i_{qdo} =D\left[ {{\begin{array}{l@{\quad }l@{\quad }l} 0&{} 1&{} 0 \\ \end{array} }} \right] \left[ {{\begin{array}{l} {i_q } \\ {i_d } \\ {i_o } \\ \end{array} }} \right] \end{aligned}$$

(44)

where $M_p$ is the Park transformation matrix:

$$\begin{aligned} M_p =\sqrt{\frac{2}{3}}\left[ {{\begin{array}{l@{\quad }l@{\quad }l} {\cos \left( {\omega _e t} \right) }&{} {cos\left( {\omega _e t-\frac{2\pi }{3}} \right) }&{} {cos\left( {\omega _e t+\frac{2\pi }{3}} \right) } \\ {\sin \left( {\omega _e t} \right) }&{} {sin\left( {\omega _e t-\frac{2\pi }{3}} \right) }&{} {sin\left( {\omega _e t+\frac{2\pi }{3}} \right) } \\ {\frac{1}{\sqrt{2}}}&{} {\frac{1}{\sqrt{2}}}&{} {\frac{1}{\sqrt{2}}} \\ \end{array} }} \right] \end{aligned}$$

(45)

The voltage on the capacitor is given by:

$$\begin{aligned} \frac{dv_{dc} }{dt}=\frac{i_{dc} }{C_{dc} } \end{aligned}$$

(46)

Combining Eqs. (44) and (46) gives:

$$\begin{aligned} \frac{dv_{dc} }{dt}=\frac{D}{2C_{dc} }i_d \end{aligned}$$

(47)

Finally, combining Eq. (47) with Eq. (42), yields the following nonlinear Park model of the source current and DC link voltage.

$$\begin{aligned} \frac{d}{dt}\left[ {{\begin{array}{l} {i_q } \\ {i_d } \\ {v_{dc} } \\ \end{array} }} \right] =\left[ {{\begin{array}{l@{\quad }l@{\quad }l} {\frac{-R_f }{L_f }}&{} {-\omega _e }&{} 0 \\ {\omega _e }&{} {\frac{-R_f }{L_f }}&{} {\frac{D}{L_f }} \\ 0&{} {\frac{D}{2C_{dc} }}&{} 0 \\ \end{array} }} \right] \left[ {{\begin{array}{l} {i_q } \\ {i_d } \\ {v_{dc} } \\ \end{array} }} \right] +\frac{1}{L_f }\left[ {{\begin{array}{l} {-V_s \sin \delta } \\ {-V_s \cos \delta } \\ 0 \\ \end{array} }} \right] \end{aligned}$$

(48)

Appendix B: Linearised model of the grid-side

From the state Eq. (46), it can be seen that the control parameter $\delta$. takes the form of $\sin \delta$ and $\cos \delta$. In addition, the state matrix depends on the inverter conversion ratio D which is not constant. Therefore, the system is non-linear. The reactive component of the current $i_q$ of the source is zero (the system is operating at unity power factor), in this case phase shift $\delta$ between the fundamental voltages of the source and those of the inverter output voltage is almost zero ($\delta \approx 0)$. The model can therefore be linearized based on the following assumptions [38]:

• The second order terms are of the perturbed variables are negliglected.

• The value $\delta _0$ operating point is zero.

The $\Delta -$notation is introduced to indicate perturbed values.

Applying a small perturbation to the system gives:

$$\begin{aligned} \left\{ {{\begin{array}{l} {\mathop i\nolimits ^{\bullet } _{q0} +\mathop i\nolimits ^{\bullet } _{q\Delta } =-\frac{R_f }{L_f }\left[ {i_{q0} -i_{q\Delta } } \right] -\omega _e \left[ {i_{d0} -i_{d\Delta } } \right] +\frac{1}{L_f }\left[ {v_{q0} +v_{q\Delta } } \right] } \\ {\mathop i\nolimits ^{\bullet } _{d0} +\mathop i\nolimits ^{\bullet } _{d\Delta } =\omega _e \left[ {i_{q0} -i_{q\Delta } } \right] -\frac{R_f }{L_f }\left[ {i_{d0} -i_{d\Delta } } \right] +\frac{1}{L_f }\left\{ {\left[ {v_{d0} +v_{d\Delta } } \right] -\left[ {v_{od0} +v_{od\Delta } } \right] } \right\} } \\ {\mathop v\nolimits ^{\bullet } _{dc0} +\mathop v\nolimits ^{\bullet } _{dc\Delta } =\left( {D+D_\Delta } \right) \left[ {v_{dc0} +v_{dc\Delta } } \right] -Dv_{dc0} } \\ \end{array} }} \right. \nonumber \\ \end{aligned}$$

(49)

where the Park transformation of the source voltage and the inverter output voltages are given by [38]:

$$\begin{aligned} \left\{ {{\begin{array}{l} {v_{q\Delta } +v_{q0} =-V_s \sin \left( {\delta _0 +\delta _\Delta } \right) +V_s \sin \left( {\delta _0 } \right) } \\ {v_{d\Delta } +v_{d0} =V_s \cos \left( {\delta _0 +\delta _\Delta } \right) -V_s \cos \left( {\delta _0 } \right) } \\ {v_{od\Delta } -v_{od0} =\left( {D+D_\Delta } \right) \left[ {v_{dc0} +v_{dc\Delta } } \right] -Dv_{dc0} } \\ \end{array} }} \right. \end{aligned}$$

(50)

Using the trigonometric development of sin($\delta$ $_{0}$ +$\delta$ $_{\Delta })$ and cos($\delta$ $_{0}$ +$\delta$ $_{\Delta })$, Eq. (50) becomeS:

$$\begin{aligned} \left\{ {{\begin{array}{l} {v_{q\Delta } +v_{q0} =-V_s \left[ {\sin \left( {\delta _0 } \right) \cos \left( {\delta _\Delta } \right) -\sin \left( {\delta _\Delta } \right) \cos \left( {\delta _0 } \right) } \right] +V_s \sin \left( {\delta _0 } \right) } \\ {v_{d\Delta } +v_{d0} =V_s \left[ {\cos \left( {\delta _0 } \right) \cos \left( {\delta _\Delta } \right) +\sin \left( {\delta _0 } \right) \sin \left( {\delta _\Delta } \right) } \right] -V_s \cos \left( {\delta _0 } \right) } \\ {v_{od\Delta } -v_{od0} =\left( {D+D_\Delta } \right) \left[ {v_{dc0} +v_{dc\Delta } } \right] -Dv_{dc0} } \\ \end{array} }} \right. \end{aligned}$$

(51)

Quantities with subscript 0 are equal to those of the initial conditions ($\delta _0 =0)$. Using the following approximations [39]:

$$\begin{aligned} \left\{ {{\begin{array}{l} {\sin \delta _\Delta \approx \delta _\Delta } \\ {\cos \delta _\Delta \approx 1} \\ \end{array} }} \right. \end{aligned}$$

(52)

The linearised model of the system (51) can be written as:

$$\begin{aligned} \left\{ {{\begin{array}{l} {v_{q\Delta } +v_{q0} =-V_s \delta _\Delta } \\ {v_{d\Delta } +v_{d0} \approx 0} \\ {v_{od\Delta } -v_{od0} \approx Dv_{dc0} +D_\Delta v_{dc\Delta } } \\ \end{array} }} \right. \end{aligned}$$

(53)

Substituting Eq. (51) into (49), and assuming that the initial value of the current source is zero gives:

$$\begin{aligned} \left\{ {{\begin{array}{l} {\frac{di_{q\Delta } }{dt}=-\frac{R_f }{L_f }i_{q\Delta } -\omega _e i_{d\Delta } -\frac{V_s }{L_f }\delta _\Delta } \\ {\frac{di_{d\Delta } }{dt}=\omega _e i_{q\Delta } -\frac{R_f }{L_f }i_{d\Delta } -\frac{1}{L_f }\left[ {-Dv_{dc\Delta } +D_\Delta v_{dc0} } \right] } \\ {\frac{dv_{dc\Delta } }{dt}=\frac{D}{2C_{dc} }i_{d\Delta } } \\ \end{array} }} \right. \end{aligned}$$

(54)

Finally, the linearised state-space model of the MIMO system can be written in matrix form as:

$$\begin{aligned} \frac{dx}{dt}=Ax+Bu \end{aligned}$$

(55)

where x is the state vector $x=\left[ {i_{q\Delta } i_{d\Delta } v_{dc\Delta } } \right] ^{T},$ and u is the input vector $u=\left[ {\delta _\Delta D_\Delta } \right] ^{T}$.

A and B are the state matrix and control or input matrix respectively and are given by

$$\begin{aligned} A=\left[ {{\begin{array}{l@{\quad }l@{\quad }l} {-\frac{R_f }{L_f }}&{} {-\omega _e }&{} 0 \\ {\omega _e }&{} {-\frac{R_f }{L_f }}&{} {-\frac{D}{L_f }} \\ 0&{} {\frac{D}{2C_{dc} }}&{} 0 \\ \end{array} }} \right] ,B=\frac{1}{L_f }\left[ {{\begin{array}{ll} {-V_s } &{} 0 \\ 0 &{} {v_{dc0} } \\ 0 &{} 0 \\ \end{array} }} \right] \end{aligned}$$

(56)

The system transfer matrix is calculated using :

$$\begin{aligned} G\left( s \right) =\frac{Y}{U}=C\left( {sI-A} \right) ^{-1}B \end{aligned}$$

(57)

$$\begin{aligned} G\left( s \right) =\frac{\left[ {{\begin{array}{ll} {-\frac{V_s }{L_f }\left( {s^{2}+\frac{R_f }{L_f }s+\frac{D^{2}}{2L_f C_{dc} }} \right) }&{} {-\frac{\omega _e v_{dc0} s}{L_f }} \\ {-\frac{\omega _e V_s s}{L_f }}&{} {\left( {s^{2}+\frac{R_f }{L_f }s} \right) \frac{v_{dc0} }{L_f }} \\ {-\frac{\omega _e V_s D}{2L_f C_{dc} }}&{} {\left( {s+\frac{R_f }{L_f }} \right) \frac{Dv_{dc0} }{2L_f C_{dc} }} \\ \end{array} }} \right] }{s^{3}+2\left( {\frac{R_f }{L_f }} \right) s^{2}+\left( {\frac{D^{2}}{2L_f C_{dc} }+\left( {\frac{R_f }{L_f }} \right) ^{2}+\omega _e^2 } \right) s+\frac{D^{2}R_f }{2L_f^2 C_{dc} }} \end{aligned}$$

(58)

Appendix C: Model parameters

See Table 1.

Table 1 Models parameters values