Introduction

Groundwater in Mexico represents 39% (33,819 million m3) of the total allocated water volume (SEMARNAT 2017). The dependency on groundwater is higher in the northern part of the country and along the borderline to United States. In this area, surface water sources are scarce or absent and more than 90% of total allocated water volume comes from groundwater (e.g., Mahlknecht et al. 2008; Tamez-Meléndez et al. 2016). Recent studies identified 36 aquifers along the 3145 km (1954 mi) US–Mexican continental border; sixteen of them have been shown to be transboundary aquifer systems (Sanchez et al. 2016). Surface and groundwater management plans and projects executed on one side of the border in these aquifers may have important implications to the neighboring country.

A bilateral agreement—the Treaty between the USA and Mexico relating to the utilization of the waters of the Colorado and Tijuana Rivers and of the Rio Grande—was enacted in 1944 to structure and manage binational conflicts between USA and Mexico, considering surface water resources. Globally, while nearly 600 transboundary aquifers and aquifer bodies have been identified, only few of them have formal, binational, or multinational mechanisms for cooperation (IGRAC 2014; Sanchez and Eckstein 2017), despite the fact that there are more than 260 river basins and transboundary aquifers that are the source of increasing levels of disagreements (United Nations Water 2008; Cortez-Lara et al. 2014).

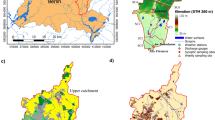
The Mexicali Valley is located at the borderline between southeastern California (USA) and northeastern Baja California (Mexico) along the lower Colorado River (Fig. 1). It encompasses a portion of the 207,234-ha (512,086 acres) Mexican Irrigation District 014, with wheat, cotton and alfalfa representing ~ 80% of the total agricultural area. In this area, surface and groundwater run over geopolitical divisions in general direction from North to South (Cortez-Lara 2015). The Mexicali Valley’s agricultural activities, irrigation, culture and history are mostly tied to flows from the Colorado River water course. Specifically, irrigation water and water for major urban and rural areas in Mexicali and Tijuana in Baja California State, and the city of San Luis Rio Colorado in Sonora State, are mainly drawn from the Colorado River. A second source is the groundwater from the Mexicali Valley aquifer, shared by the USA and Mexico. Water supply from this aquifer has been largely contested between both countries, and this fact has brought about controversies concerning the use of rights over groundwater (Cortez-Lara et al. 2009; Cortez-Lara 2015).

Fig. 1
figure 1

Location of study area, topography with main features, AAC lining project, modeled area with groundwater wells (red dots)

Full size image

In the 1930s, the US Bureau of Reclamation constructed the 42-km long All-American Canal (AAC) in Southern California and began delivering water in the 1940s. It conveys about 3453 hm3 (2799 acre-feet) of Colorado River water annually for use in the Imperial irrigation district and Coachella Valley water district service areas in California. It begins at the Imperial dam located north of Yuma, Arizona, and generally parallels the US–Mexican border to its terminals in the western Imperial Valley. The unlined AAC is porous and Colorado River water has seeped into the ground since its construction in the 1930s, with beneficial effects for agriculture in Mexicali Valley.

Prior to the AAC construction, depth to groundwater in the area was about 15 m below the AAC. Water infiltration from the AAC has raised the groundwater levels. In areas between Point Knob and Drop 2, depths to groundwater ranged from 3 m to 6 m below the AAC in the late 1980s (US Bureau of Reclamation 1990). It was estimated that the loss through infiltration was about 84 hm3 (68.1 acre-feet) per year. Of this, about 5% (4 hm3) were taken up by natural vegetation, 10% (8 hm3/year) flowed into the Imperial Valley and 85% (72 hm3/year) flowed into the Mexicali Valley (Fig. 2). From the 72 hm3/year that flowed into Mexico, 24 hm3/year entered La Mesa drain and 48 hm3/year supplied the Mexicali Valley (CONAGUA 2005; WMO 2009), representing an important water source for Mexicali’s agriculture. In November 1989, the US Congress authorized the lining of the AAC to recover the infiltration losses. The lining project extends 37 km (23 mi) starting 1.5 km (0.9 mi) west of Pilot Knob and ending at Drop 3 (CONAGUA 2005).

Fig. 2
figure 2

Modified from CONAGUA (2005)

Volume of water infiltrated by the AAC prior to the lining

Full size image

The lining of a portion of the AAC, concluded by the US government in 2008, is expected to negatively affect the Mexicali Valley. These negative effects refer mainly to groundwater level drawdowns. Groundwater levels in piezometers within a distance of 1.5 km from AAC were reported to decline between 1.43 and 1.93 m/year between September 2008 and December 2010 (WMO 2009).

Based on this trend and concern, this study evaluated the effects of the AAC lining on groundwater levels at the Mexican side. The objectives of this work were: (i) to develop a conceptual model of the aquifer on the northeastern portion of the Valley of Mexicali, Baja California State; (ii) to create a numerical groundwater flow model of this portion that reproduces the effects of the AAC lining; and (iii) to generate future scenarios according to different groundwater management schemes.

Although the lining project has generated a controversy due to the obvious impact on Mexican groundwater resources and ecosystems (Cortez-Lara et al. 2014), to our knowledge, there has been little effort to address these concerns using a quantitative approach. A challenging situation of this study area is that, although there is a vast amount of information available on extraction rates and groundwater levels during the last 80 years, the monitoring and reporting was intermittent, while at the same time the stresses and forces were very variable over time.

Case study area

The Mexicali Valley is located northeast of the peninsula of Baja California, south of the Imperial Valley in California. Hydrologically, it is located in the Colorado River basin that forms one of the most important international water systems of the US–Mexico border, supplying water through seven US states and Mexico. Mexicali has a dry, arid climate with winter rainfall and one of the most extreme climates in Mexico, with average July high temperature of 42.2 °C (108 °F), and average January high temperature of 21.1 °C (70 °F). It receives on average 75 mm (2.95 in) of rain annually (García Cueto et al. 2013). Physiographically, this area is part of the Sonoran desert province. The main economic activities in Mexicali Valley are agriculture and geothermal electric power generation (Fuentes-Arreazola et al. 2018). The primary sources of water for irrigation are surface water from the Colorado River and groundwater from the Mexicali aquifer.

Geology

Regionally, the Mexicali Valley is located in the Salton Trough, which is part of the San Andreas Gulf of California fault system that corresponds to the boundary between the Pacific and North American tectonic plates (Stock et al. 1991). Locally, no major faults have been detected. A 5000-m deep basin was created by fault movements, which was filled by sediments from the Colorado River, as well as transported eroded debris from the Colorado Plateau basin margins (Suárez-Vidal et al. 2008). The transmissive sediments in the basin can be divided into two units—lower consolidated and upper unconsolidated sediments—separated by strata with a very low permeability (Lira 2005). The upper unconsolidated sediments have a variable thickness of 400–2500 m and contain the Mexicali Valley aquifer (Álvarez-Rosales 1999; Fuentes-Arreazola et al. 2018). From borehole data, it can be inferred that the thickness of these unconsolidated deltaic sediments in the study area are at least 800 m (CICESE 1998; CONAGUA 2005; WMO 2009, 2010). They are of fine to coarse sands with intercalations of gravel, clays and silts (Lyons and van de Kamp 1980; Portugal et al. 2005) (Fig. 3).

Fig. 3
figure 3

Modified from CONAGUA (2005)

W–E geological cross-section of the Mexicali Valley (sands in yellow, clays in orange)

Full size image

The modeled portion of the Mexicali Valley is a large flat area, located a few meters above sea level (masl) (Fig. 1). The eastern portion of the studied area includes the floodplain of the Colorado River, which comes from the US and runs south, emptying into the Gulf of California. The runoff from this river was substantial in the past. Currently, dams in the US control the Colorado River, while its riverbed on the Mexican side is currently dry. There are practically no streams in the rest of the studied area. On the northern portion of the Mexicali Valley, there is a plateau known as Mesa de Andrade. This plateau rises about 20 m above the floodplain and is formed by sands. The main morphological feature in the plateau is the presence of dunes, typical of sandy deserts.

Historical evolution and operative conditions

The Mexicali Valley aquifer has a vast amount of information starting 80 years ago. However, the discontinuity of reports makes it challenging to establish stress periods for the model. The compiled information varies mainly in the uniformity of pumping well flow rates and groundwater recharge data through irrigation. The operative conditions and conceptual model of the aquifer are summarized as follows (Fig. 4):

Fig. 4
figure 4

Operational conditions to establish the numerical model of the AAC and northern portion of the Mexicali aquifer

Full size image
  1. 1.

    The operation of the AAC started in 1939, and infiltration into the underlying aquifer began immediately. Between the years 1957 and 1960, a potentiometric dome stabilized in the vicinity of the AAC. Lining of the AAC was completed in 2008.

  2. 2.

    Water infiltration from the AAC started in 1939. In 1960, an infiltration of 80 hm3/year was reported, of which 72 hm3/year circulated into Mexico. Of 72 hm3/year, 24 hm3/year were captured by La Mesa drain, and 48 hm3/year supplied to the Mexicali Valley aquifer (CONAGUA 2005). It is estimated that this infiltration rate remained constant until 2008. Due to the lining of the AAC, the infiltration rate decreased to 23 hm3/year in 2009. It is estimated that in 2012 the infiltration was close to zero (WMO 2009).

  3. 3.

    Groundwater levels for the aquifer of Mexicali Valley are available for 32 years (1957, 1979–1982, 1984–1995 and 1998–2012). From 2005 on, groundwater levels were monitored on a monthly basis (WMO 2010; CONAGUA 2012).

  4. 4.

    There is information about annual extraction rates for all pumping wells in 5 specific years (1984, 1987, 1992, 2000 and 2001). For all years between 1957 and 2012, the total amount of groundwater withdrawn from the aquifer is known (CONAGUA 2006, 2012). For those years, where individual annual extraction rates are not known, these were estimated based on the contribution of each individual well on the withdrawal from the whole aquifer, resulting in a dataset of annual flow rates for 300 production wells in the period 1957–2012. Of these, 202 wells were active in 1957, while 230 were active in 2012.

  5. 5.

    The highest extraction rates were reported from 1953 to 1980, creating constant drops in the water level of the aquifer. From 1980 to 1986, there were large surpluses of surface water from the US through the Colorado River. These surpluses were used for the agriculture, and infiltration from agricultural irrigation provided additional recharge into the aquifer. From 1987 to 2004, there was a relatively constant extraction rate and groundwater levels stabilized in general.

  6. 6.

    There is information about the volumes of water discharging from La Mesa Drain. From 1960 to 2005, a constant flow rate of 1600 lps (liters per second) was reported. In 2006 the discharge decreased to 557 lps (WMO 2010). From 2007 to 2012 the water outcropping at the drain was reported on an annual basis and the trend of decrease continued until it was negligible in 2012 (CONAGUA 2012; WMO 2010). Groundwater also outcrops at the Culiacan Drain, having a constant rate of 200 lps from 1960 to 2012 (CONAGUA 2012).

Materials

Numerical model

A mathematical model is often used in hydrogeology to address nontrivial questions (Bredehoeft and Hall 1995). It provides a quantitative framework for synthesizing field information and for conceptualizing hydrogeological processes (Anderson and Woessner 1992). Finite-difference methods allow for both steady-state and transient groundwater flow in three dimensions in heterogeneous media with complex boundaries and a complex combination of sources and sinks of water. Owing their versatility, they are most commonly used to solve groundwater problems (Anderson et al. 2015). The applied finite-difference method for solving groundwater flow equations in the heterogeneous media of the Mexicali Valley was MODFLOW (Harbaugh 2005).

Groundwater movement through porous materials of constant density can be described in three dimensions using the general groundwater flow Eq. (1), which is based on Darcy’s law:

$$\nabla \left( {k\nabla h} \right) + W\left( {x,y,z} \right) = {\text{Ss}}\frac{\delta h}{\delta t}$$
(1)

where K is hydraulic conductivity (LT−1), h is hydraulic head (L), W is volumetric flux per unit volume (representing sources and/or sinks), x and y are horizontal coordinates (L), z is vertical coordinate (L), Ss is specific storage and t is time (T) (Harbaugh 2005).

According to the principle of parsimony, groundwater flow models are always simplifications of real hydrogeological systems (Hill 2006; Zhou and Li 2011). The simplifications for this study area were that complex geological formations were reduced to a limited number of hydrogeological layers with assumed physical boundaries, dominant flow processes were considered in the model simulation, and parameter zones were defined to simplify the input of model parameters.

Model setup and geometry

The model domain was delimited taking into account the most important elements of the modeled area, i.e., the AAC, the Mesa de Andrade, La Mesa Drain, Culiacan Drain, the network of 43 monitoring wells established in 2008 to observe the groundwater level changes produced by the lining of the AAC, of which 38 were measured in 2012, the year that served for calibration. This was in addition to data from the 300 extraction wells located in the study area.

The aquifer was conceptualized as an 800-m-thick granular sediment material divided into 5 layers (Fig. 5). It was determined that the inflow to the aquifer consists of groundwater inflow coming from the north, return flow from irrigation and secondary canals covering a large area of the valley, infiltration from main unlined canals and infiltration along the bed of the Colorado River. Infiltration through main canals is now negligible, since they are mostly lined, however, in previous decades this was an important factor which was taken into account for the reconstruction of the history of the aquifer. The infiltration along the riverbed of the Colorado River has also been reduced in recent years to negligible, since all its flow has been redirected now through canals. It was also determined that the outflows from the aquifer consisted of extraction through wells, groundwater discharge south of the study area and drains (Fig. 5).

Fig. 5
figure 5

Conceptual model of the northern portion of the Mexicali Valley aquifer

Full size image

The model domain was framed using Universal Transverse Marcator (UTM) coordinates. The catchment area was 1250 km2, with grid cells spaced at 200 m × 200 m. The grid contained 250 columns (X axis) and 124 rows (Y axis) for each of the five layers. Active cells include the valley area and inactive cells were assigned to the surroundings (Fig. 6).

Fig. 6
figure 6

Model domain, active cells (white), inactive cells (light blue), general head boundary (green), drain boundary (light gray), river boundary (AAC and Colorado River) (navy blue). The 43 monitoring wells established in 2008 (purple) and 44 monitoring wells measured prior to this date are also shown (red)

Full size image

Ground surface for the model domain was imported from digitized topography (INEGI 2006). With respect to vertical discretization (number of layers), it was taken into account that there are approximately 800 m of saturated alluvium. Borehole information indicates that these sediments correspond to a single, heterogeneous, hydrogeologic unit. There is no evidence or data to suggest splitting this layer geologically. There are lateral changes of facies, which are modeled with zones with different hydrodynamic properties of the aquifer as described in the following sections. It was also taken into account that most wells, for sanitary purposes, have cemented casings in the upper 100 m. The depth of exploitation of most wells is from 100 to 250 m deep. It was arbitrarily assumed that below 800 m of depth, groundwater flow is not influenced by pumping. Hence, it was determined to establish three upper layers where exploitation takes place to allow for vertical movement of groundwater, and two bottom layers working as buffer zones. The bases for the layers were at depths of ~ 100, 200, 300, 500 and 800 m below surface, correspondingly.

Hydrodynamic properties

Information from 35 pumping well tests (CONAGUA 2006) was compiled and re-analyzed. Aquifer transmissivity was found to vary from 0.03 to 0.08 m2/s at the center of the studied area, and from 0.02 to 0.03 m2/s at the western portion. Pumping tests at Mesa de Andrade indicate intermediate values ranging from 0.02 to 0.06 m2/s (CONAGUA 2012). These transmissivities were used as a basis to feed the model with hydraulic conductivity values, using the relationship (Eq. 2):

$$K = \frac{T}{b}$$
(2)

where K is the hydraulic conductivity (m/s), T is the aquifer transmissivity (m2/s) and b is the aquifer thickness (m).

Considering well depths, an average aquifer thickness of 300 m was assumed, and based on pumping tests, hydraulic conductivity values were estimated ranging from 6 × 10−5 to 3 × 10−4 m/s. Hydraulic conductivity zones and values were adjusted during model calibration, while maintaining a scenario where hydraulic conductivities were lower in the west than the east and within the estimated limits. The calibrated Kx and Ky values varied from 8 × 10−5 to 3.5 × 10−4 m/s for the upper portion of the aquifer (Fig. 7a), and from 3 × 10−5 to 8 × 10−5 m/s for the lower layers (Fig. 7d). The storage coefficients were obtained from field data, grain size of field materials and commonly used values from literature (CONAGUA 1996, 2001, 2006; Díaz-Cabrera 2001; Freeze and Cherry 1979), and were adjusted during the calibration process. The calibrated values and distribution of storage coefficients in the upper three layers of the aquifer are shown in Fig. 7b. In the two bottom layers, the value of Ss was homogeneously set to 0.0001 and Sy to 0.1. The porosity in all the aquifer was set at 0.25.

Fig. 7
figure 7

Hydrodynamic parameter data assignation and distribution: a hydraulic conductivities in the top three layers (in m/s); b hydraulic conductivities in the two bottom layers (in m/s); c storage coefficient in the top three layers (unitless); d vertical recharge by precipitation and return flow from irrigation and channels in mm/year

Full size image

Boundary conditions

In 1930, the static water level was 15 m below the AAC (US Bureau of Reclamation 1990). Of the 56 years between 1957 and 2012, there are 32 years with records of static water levels at monitoring wells (CONAGUA 2012). These records include a total of 88 monitoring wells, of which not all were monitored every year. Potentiometric data were included in the model to be used for calibration.

With the information collected, static water level contour maps were created for 32 different years. From these, the most relevant were: 1957 (earliest data available), 1984 (high number of monitoring wells measured), 2008 (lining of the AAC) and 2012 (static groundwater levels monitored in this study). In addition, groundwater level evolution maps were created for different periods, the most representative were 1939–1972 and 2008–2011.

The initial hydraulic heads for the model were those measured in the starting year (1957). The vertical recharge is the infiltration generated in the valley by precipitation, infiltration from unlined secondary channels and infiltration from irrigation. All this information was analyzed and the calculated total infiltration used as input for the model (Fig. 7d). The irrigation losses varied through time in zone 1, and remained constant through the rest of the modeled area. This water balance throughout most of the valley is due to the decrease in pumping from wells when there are surpluses of surface water flowing from the US into Mexico through the Colorado River.

A general head boundary (GHB) was used to simulate head-dependent flux boundaries, with the flux being proportional to the difference in head. The model was supplied with a hydraulic head value outside the model domain, and the flow was calculated from this hydraulic head to the boundary cell using the conductance, a value that cannot be measured in the field and is obtained by model calibration or using the following approximation (Harbaugh 2005):

$$C = \frac{KA}{L}$$
(3)

where C is the conductance, K is the average hydraulic conductivity of the material between the “far” head and cell where the boundary is assigned, A is the area of the cell through which the groundwater flows, L is the distance between the “far” head and the assigned boundary.

GHB cells were assigned at the northern edge of the modeled area (at the limit with the inactive cells) to simulate groundwater inflow from the north. Likewise, GHB boundaries were assigned at the southern boundary of the modeled area, to simulate groundwater outflow from the modeled area (Fig. 6). GHB were assigned through the five layers of the model. The “far” head did not change through the layers, however, the conductance was different for the upper three layers from the bottom three layers (Table S1).

La Mesa drain

A drain boundary requires a conductance value such as the GHB, which is also adjusted during the calibration process. The conductance for a drain boundary was estimated using the following equation:

$$C = \frac{KLW}{M}$$
(4)

where W is the width of the cell and M is thickness of sediments deposited at the base of the drain.

La Mesa drain is located south of the Mesa de Andrade plateau, just where the topography drops about 20 m into the valley (Fig. 6). A constant volume of 1600 lps was reported at La Mesa Drain from 1960 until 2006, when it was reported to be a volume of 557 lps (WMO 2010). From 2007 to 2012, water outcropping at the drain was decreasing (Table S2). In 2012, only 23 lps were measured at the exit control point located outside the modeled area (CONAGUA 2012).

The AAC and the Colorado River

The AAC was the main canal recharge to the aquifer from 1939 to 2008. The Colorado River was also an important groundwater recharge until the year 2000. They both were modeled using the river boundary (Fig. 6). To simulate the AAC lining, the value of the conductance was set to zero (Table S3). To simulate the flow reduction in the Colorado River, the water depth of the river was reduced.

There is a vast amount of information on the extraction from the Mexicali Valley aquifer, however, it is scattered and incomplete for several periods. After a thorough analysis, a database of annual extraction flow rates from pumping wells was created. In some years, these pumping rates were direct measurements on each individual well, in other years these values were estimated as contributions to the total volume of water pumped for the whole irrigation district.

Concretely, there is information on flow rates for each well in five specific years (1984, 1987, 1992, 2000 and 2001). For all years from 1957 to 2012, the total amount of groundwater extracted from the aquifer is known through the control established by each irrigation district (CONAGUA 2006, 2012). The individual contribution of wells to the total extraction was calculated as percentage for the known years, and the total amount of water withdrawn from the aquifer each year was used together with the percentages of individual wells to calculate the extraction rate for each well for the other years in the period 1957–2012.

Hence, although there is a large amount of flow rates information, there are ranges with gaps that were filled with estimated values. This creates a degree of uncertainty in the calibration of the numerical model. Data for 300 pumping wells were included in the model considering the geographical location, slotted casing depth, total well depth, cemented casing depth and extraction rate for each modeled year. Most wells have a cemented casing on the upper 100 m.

Calibration of model

The calibration of a model refers to the demonstration that a model is able to reproduce the behavior of the aquifer, which is generally verified by comparing the model results with field measurements (Hill and Tiedeman 2007). Model calibration does not give unique results, i.e., there may be different combinations of data that can calibrate a model. With more field data available, the model will be more robust.

Calibration can be performed at steady or transient state. The model was run at transient state since it reproduces the behavior of an aquifer over time. The model was calibrated by the method of trial and error, changing areas and values of hydraulic conductivity, storage, recharge and boundaries, within acceptable ranges and supported with the available information.

For the evaluation of the effectiveness of the model, qualitative and quantitative assessments were done. Regarding the qualitative assessment, the observed hydraulic head contour lines were compared with simulated contour lines in maps, to identify outliers and bias of the model. On the other hand, the quantitative assessment was carried out comparing measured versus calculated hydraulic heads using the normalized root mean square error (NRMSE) that helps to identify the error measured in the units of interest (Eqs. 5 and 6).

$${\text{RMSE}}\; = \;\sqrt {\frac{{\sum \left( {y - x} \right)^{2} }}{N}}$$
(5)
$${\text{NRMSE}} = \frac{\text{RMSE}}{{x_{ \text{max} } - x_{\text{min} } }}$$
(6)

where x is the observed value; y is the simulated value; N is the total number of values; and xmax and xmin are the maximum and minimum observed values.

Qualitative, quantitative and mass balance calibrations were performed for the year 2012. Then, after analyzing the historic available data, calibrations were done simultaneously for different years, trying to maintain a water balance for all years for all calibration methods employed. The years chosen for calibration were based on events:

  • Year 1957—Stabilization of the potentiometric dome.

  • Year 1984—Highest reported groundwater table drawdowns.

  • Year 2008—Lining of the AAC started.

  • Year 2011—The first effects of the AAC lining clearly observed in the aquifer.

  • Year 2012—Last year with information.

Results and discussion

Groundwater levels

With the information collected and measured in this study, water table maps from different years were generated. The most representative were from the years 1957, 1984, 2008 and 2012 (Fig. 8). It shows that the flow pattern has been consistent since 1957, with equipotential lines somehow parallel to the border and groundwater flowing to the south–southwest. The highest groundwater elevations in the modeled area were 30 and 35 masl along the border. These groundwater levels decreased to 20 masl south of the study area in 1957, to 17 masl in 1984 and to 13 masl from 2008 and onwards. In the northern portion of the study area, a potentiometric dome formed due to infiltration from the AAC, and gradually started to disappear in 2009 (Fig. 8).

Fig. 8
figure 8

Water table contour maps for the years 1957 (a), 1984 (b), 2008 (c), and 2012 (d)

Full size image

Infiltration from AAC seepage resulted in the rise of groundwater levels in the Mexicali Valley aquifer over the years. The potentiometric history in the Mexicali Valley shows that from 1939 to 1972, groundwater levels increased up to 14 m in the AAC area, creating a dome (US Bureau of Reclamation 1987; Fig. 8a). In the southern portion of the study area, groundwater levels did not show any change in the same period.

Some groundwater drawdowns have been detected in the area, mostly since the lining of the AAC in 2008. These drawdowns are more pronounced in wells and piezometers located near the AAC. As an example, in 1930, the area near to Drop 2 had depths to the water table of 15 m below the AAC (US Bureau of Reclamation 1990). Water levels in this area increased due to the ACC infiltrations, and in 2008 the monitoring well BC10-CNA2, located in this area, reported a depth to the water level of 4.5 m below the AAC (recovery of 11.5 m up to 2008). For the year 2012, the water level at this well had decreased to 10.0 m below the AAC, which means a drawdown of 5.5 m in 4 years (CONAGUA 2012). This shows the effect of the AAC increasing water levels from 1930 to 2008, and then the effect of the AAC lining, lowering the water levels since 2008.

Groundwater dropped 4.0 m near the border during 2008–2011, which translates into a 1.3 m drawdown per year. In the southern portion of the study area, groundwater levels did not show any change. From 2008 to 2012, wells near the border reported drawdowns ranging from 3.53 to 5.76 m (CONAGUA 2012). Monitoring well BC10-CNA2 is representative of all the areas where the AAC was lined, and showed that the water table tended to stabilize to the groundwater level that existed in 1930, prior to the effect of the infiltrations from the AAC.

Model calibration

Groundwater levels measured on each monitoring well were compared to those calculated by the model. The model reproduced acceptably the measured equipotential lines for the relevant years 1957, 1984, 2008, 2011 and 2012. Figure 9 shows as an example of the results for the year 2012. The normalized root mean squared error (NRMSE) for stress periods corresponding to the calibrated years ranged from 5.5 to 16.3% (Fig. 10). The amount of monitoring wells for each stress period ranged from 21 to 39 (Table 1). These were the amounts of monitoring wells used for both the qualitative calibration comparing with a hand-drawn calibration and the quantitative calibration of observed vs. calculated heads plots.

Fig. 9
figure 9

Observed (red) and simulated (blue) contour lines for the year 2012

Full size image
Fig. 10
figure 10

Calculated vs. observed heads for the calibration years (1957, 1984, 2008, 2011 and 2012)

Full size image
Table 1 Normalized root mean squared error (NRMSE) and the amount of monitoring wells employed for each calibrated stress period
Full size table

Calibration was also done by performing a groundwater balance in the modeled area. A groundwater balance can be calculated by estimating the following parameters:

$$I\; - \;O\; = \; \pm \;\Delta S$$
(7)

where I is the total groundwater inflow, O is the total groundwater outflow, ΔS is the change in groundwater storage. Further:

$$I\; = \;I_{\text{GW}} \; + \;I_{\text{VInf}}$$
(8)

and

$$O\; = \;E\; + \;O_{\text{GW}} \; + \;D$$
(9)

where IGW is the inflow as groundwater flow, IVInf is the vertical infiltration from unlined channels and irrigation, E is the withdrawal by groundwater extraction, OGW is the outflow as groundwater flow, and D is the groundwater outflow through drains. Then:

$$I_{\text{GW}} \; + \;I_{\text{VInf}} \; - \;E\; - \;O_{\text{GW}} \; - \;D\; = \; \pm \;\Delta S.$$
(10)

Groundwater balances were prepared for years 2008 and 2011, because these years had enough information to perform detailed groundwater balances. Groundwater inflow and outflow were determined applying Darcy’s law on inflow and outflow cells drawn on equipotential contour maps. Groundwater extraction volumes and drain water were obtained from revised information (CONAGUA 2006, 2012). The change in groundwater storage was calculated from groundwater evolution contour maps and storativity values. The results are summarized in Table 2.

Table 2 Results from groundwater balances for the years 2008 and 2011
Full size table

The inflow as groundwater (IGW), determined in the groundwater balance, would be equivalent to the inflow produced by the sum of the general head boundary (GHBIN) and the river boundary (river) in the model. The vertical infiltration from unlined channels and irrigation (IVInf) from the groundwater balance would be equivalent to the vertical recharge boundary (recharge) in the model. Outflow as groundwater flow (OGW) from the groundwater balance would be equivalent to the outflow produced by the general head boundary (GHBOUT) in the model.

The groundwater balance calculated for 2008 was used to calibrate the model for the year 2008. In addition, since the aquifer balance did not seem to have been altered much through time from the creation of the AAC to its lining in 2008, this balance was used to estimate a certain degree of calibration for model mass balances for the years 1957 and 1984 (it should be noted that in 1957 the drain still did not work). These dates yielded reasonable matches between the groundwater balance and that estimated by the model. Likewise, the groundwater balance performed for the year 2011 was used to calibrate the model in 2011 and 2012, obtaining very good matches (Table 3).

Table 3 Comparison of groundwater balances
Full size table

Sensitivity analysis

Once the model was calibrated, a sensitivity analysis was performed. Different runs were executed in which key parameters were varied by increasing or decreasing its value by 20% and 40%. After each run, the NRMSE errors were analyzed and compared to the NRMSE obtained during calibration for the year 2012, which was 5.5%. The sensitivity analysis was performed on storage coefficients, hydraulic conductivities, vertical recharge, groundwater pumping rates and general head boundary. The variations for these values were performed evenly throughout the model.

The results show that the model is practically insensitive to changes in storage coefficients (Fig. 11). The model was slightly more sensitive to changes in hydraulic conductivity, noting that an increase in hydraulic conductivity decreased marginally the NRMSE error, however, this calibration would alter the groundwater mass balance calibration. The model was more sensitive to changes in vertical recharge. The sensitivity of the model was even larger and more noticeable with variations in extraction rates. Finally, the model was highly sensitive to changes in the general head boundary (groundwater inflow/outflow) (Fig. 11).

Fig. 11
figure 11

Sensitivity analysis: summary of NRMS errors for key calibration parameters

Full size image

These sensitivities show that it is necessary to have a good estimate of groundwater inflow/outflow through detailed field hydrogeologic studies. These results show that to obtain a better model, it would be necessary to extend the model to a larger area and decrease the sensitivity to the GHB boundaries.

It is also necessarily to determine more accurately current extraction flow rates for each well, especially since there is information about extraction flow rates per well only for few specific years. The last year with measured flow rates individually per well was in 2001. It is also necessary to conduct studies to determine more precisely the different areas with induced vertical recharge and the values from irrigation returns and infiltration by canals.

Forecasting simulations

Upon completion of the calibration process and sensitivity analysis, the forecasting of the evolution of the aquifer under proposed actions was performed. The forecasted scenarios were in accordance to the water supply schemes for the Mexicali area. The simulations were performed for the years 2017, 2022 and 2027. To perform these simulations, the following modifications were done to the calibrated model:

  • The values of GHB boundaries in recharge areas (groundwater inflow) were extended in time, decreasing the value of the hydraulic heads according to the projection of future drawdown of water levels in the area of the AAC.

  • The values of GHB boundaries in discharge areas (groundwater outflow) were extended in time without any modifications from their last values.

  • The values for the drain boundaries were extended in time, without any modifications from the last values. This boundary will have no effect on groundwater levels once these levels have decreased enough near the drain to avoid being captured by it. This was already happening in 2012 for some portions of the drain, and could be appreciated on the decline of water being captured by the drain boundary.

  • Vertical recharge values were extended in time without any modification of the last value in the simulation.

  • Extraction rates for all active wells in 2012 were extended for all the simulation time.

  • The river boundary was no longer active in the latest simulation years, then it was not necessary to extend their values over time.

  • The initial conditions and physical characteristics of the model such as hydraulic conductivity, storage coefficients and discretization do not require any modification to perform the simulations.

Scenario 1

The aquifer behavior was simulated assuming that none of the variables varied except for GHB inflow. This would be considered a baseline forecast scenario. In this forecast, for the year 2017, a drawdown of 2.5 m was observed in the northern area of the model, near the AAC. In the rest of the model, only a minimum drawdown was observed. Within the next 5 years (year 2022), a cumulative drawdown of 5 m was observed in the AAC area, while in the rest of the model this parameter was between 2 and 3 m. From 2022 to 2027, drawdowns continue throughout the model, however, these are minor (< 0.2 m per year). In the wetlands, groundwater levels will drop to about 1 m through this 15-year period. The results of this simulation support the idea that the lining of the AAC will produce a drawdown on the aquifer to groundwater levels similar to those that existed prior to the infiltrations produced by the AAC.

Scenario 2

The aquifer behavior was simulated with the addition of six wells north of the wetlands (upstream from them) in the Mesa de Andrade. This area is located just south of the AAC, between Drops 2 and 3. The purpose of this scenario was to evaluate the idea of local water authorities to drill wells in this area for additional water supply. The pumping rate for each well was set at 50 lps (total of 300 lps or 9.5 hm3/year) which is a medium to low pumping rate for wells in the vicinity. All other model variables remain fixed. For the year 2027, a 2-m drawdown near these extraction wells was observed. Away from them, the effect in groundwater levels is minimal, however, this effect would be enough to dry out the wetland.

Scenario 3

In accordance to the water supply schemes for the Mexicali area, the aquifer behavior was simulated with the addition of 15 pumping wells located south of the AAC (2 km south of the border, Fig. 12). The extraction rate for each well was set to 150 lps (total of 2250 lps or 71 hm3/year), which would be the maximum expected extraction rate per well in this area. All other model variables remain unchanged. For the year 2017, a drawdown of 10.0 m was observed near these wells, a drawdown of 2.5 m in the area south of the Mesa de Andrade, and a drawdown of 2.0 m on the northeastern portion of the model, but no significant changes in the southern portion of the model. By the year 2022, the accumulated drawdown near of the wells is 13 m, in the area south of the Mesa de Andrade is 3 m (just 0.5 m in the last 5 years), an accumulated 3.5 m of drawdown on the northeastern portion of the model (just 0.5 m in the last 5 years), and 1 m drawdown in the southern portion of the model. For the year 2027, the accumulated drawdown near the pumping wells is 16 m, in the area south of the Mesa de Andrade is 3.5 m, in the southern portion of the model 1.5 m, and to the northeastern portion there is an accumulated drawdown of 5 m (Fig. 12). The greatest drawdown is observed in the vicinity of the extraction wells, with just over 1 m/year. However, after the 15 years of simulation, no stabilization of groundwater levels in this area could be observed. Thus, the drop in a 20- or 25-year period would probably continue to increase.

Fig. 12
figure 12

Drawdown to the year 2027 according to simulation with 15 extraction wells south of the AAC, with an added extraction rate of 71 hm3/year

Full size image

Conclusions

This investigation presents the case of Mexicali Valley aquifer representing a highly contested transboundary aquifer at US–Mexican border. This investigation attempted to address the hydrodynamic effects of the construction of the All-American Canal in the 1930s and its lining in the 2000s from USA on groundwater resources in Mexicali Valley, Mexico.

Starting in the 1940s, the infiltration from the All-American Canal seepage resulted in the rise of groundwater levels in the Mexicali Valley aquifer. From 1939 to 1972, groundwater levels increased up to 14 m in the All-American Canal area, creating a groundwater dome producing benefic effects on the agriculture in Mexicali Valley. On the other hand, the lining of the All-American Canal in 2008 started a gradual process of drawdown in groundwater levels in its vicinity. Drawdowns of up to 5.8 m have been observed in 4 years at monitoring wells close to the All-American Canal. It appears that groundwater levels tend to stabilize to those that existed prior to the infiltrations produced by the All-American Canal.

A groundwater flow model was prepared for the affected portion of the Mexicali Valley aquifer. Although available information was not continuous over time, it was possible to run the model from 1957 to 2012 and calibrate it by comparing groundwater elevation contour maps, measuring the normalized error (NRMSE) between observed and modeled water levels at monitoring wells, and compare observed with modeled groundwater balances for the model domain.

A sensitivity analysis demonstrated that the model is practically insensitive to changes in storage coefficients. It is slightly more sensitive to changes in hydraulic conductivity, and is even more sensitive to changes in vertical recharge. The sensitivity of the model is larger and more noticeable with variations in wells’ pumping rates and general head boundaries, which represent groundwater inflow and outflows in the model. This shows that to obtain a better model, it would be necessary to extend the model to a larger area and decrease the sensitivity to the GHB boundaries.

The aquifer behavior was simulated assuming that none of the variables varied except for general head inflow. From the year 2012 to 2022, a cumulative drawdown of 5 m was observed near the All-American Canal area. These results support the idea that the lining of the AAC will produce a drawdown on the aquifer to groundwater levels similar to those that existed prior to the infiltrations produced by the All-American Canal. At the existing wetlands, a 1 m drawdown will be registered due to the lining, which may affect the existing ecosystem. Any additional pumping done on the Mesa de Andrade will likely dry the wetland.

Because the model is highly sensitive to pumping extraction rates, it is recommended to increase the accuracy of these estimates by performing discharge flow rate measurements at each well, at least once a year. A new groundwater model would greatly benefit by a finer grid, updated groundwater levels and specially by extending the model extents to decrease its sensitivity to groundwater inflows and outflows.