1 Introduction

The analysis of papers citation is a useful tool for evaluating the quality and influence of academic entities for authors, papers, and publication venues. It is used to evaluate research articles, authors, and venues. With a few exceptions Science, Nature, and PLOS ONE, high-level publication venues are generally subject specialized, according to popular belief. In recent years, the use of citation data assessment has gotten a lot of attention in Moed (2005). The goal is to use an article's citation rate to calculate a quantifiable estimate of its importance. It is possible to do individual and group assessments as well as article evaluations by categorizing articles according to researchers (i.e., the authors of the articles), research groups, research institutions, and nations.

There are several objections to using citation data to evaluate research. However, among the statistical indicators now available, the citation rate is undeniably the best suited for evaluating an element of research relevance (degree of effect or usage of publications). Citation data can be utilized in study evaluation if done carefully and constraints are taken into account in Abramo and D’Angelo (2015). It should be highlighted, however, that research should be assessed from a variety of perspectives, and citation rates are one of these perspectives. Citation-based metrics are not objective indications in and of themselves, but they are a useful supplement to subjective peer assessment. Even though it is widely acknowledged that an article's citation count is an effective indicator of its relevance, the count of an individual piece does not necessarily correspond to the item's rating in Moed (2006).

In a publication, the most essential item is its citation. The goal of this study is to see how the number of co-authors affects the number of citations in research papers. The measurement impact of a research article shows us the value of research, almost carried out by the primary author and co-authors who have the same notion about the subject being investigated. Various research were done on certain aspects that might impact an article's citation rate in Pal and Bharati (2019). The purpose of this research is to study how the number of co-authors affects research publishing quotations. We will analyze how co-authors count and cite research articles and examine how co-authors count the effects on publication citations. In order to rate a publication, its citation is the most essential factor. Measuring the effect of a research article informs us about the significance of the study, which usually always has a lead author and additional co-authors who share the same viewpoint on the research issue. Several studies have been done on numerous aspects that may impact an article's citation rate. There will be a correlation study between the number of co-authors and the number of citations for research papers, and we will examine how the number of co-authors affects the number of citations for publications.

In this paper, We use two methods to examine the impact of co-author count on the number of citations in a research paper: (i) Pearson's correlation coefficient (PCC), and (ii) multiple regression (MR). The goal of multiple linear regression (MLR) is to model the linear relationship between the explanatory (independent) variables and response (dependent) variables to test the mutual effect of multiple features on the citation. The main originality of this paper is to introduce an effective prediction module (EPM) which uses a probabilistic neural network (PNN) to predict the number of citations from the most effective factors (NA, NC, VC, and YF).

The results have proven that PNN has the best prediction accuracy. EPM achieved the highest accuracy due to the advantages of PNN in Talaat et al. (2020). which are: (i) PNN networks predict target probability scores with high accuracy. (ii) because there is no return (feedback) to the network in PNNs, they are much faster than multilayer perceptron networks. (iii) As the size of the representative training set grows, it is guaranteed to converge to an optimal classifier. (iv) Outliers aren't as noticeable in PNN networks.

By using a clustering method to put authors with similar backgrounds together, the proposed algorithm can be enhanced. However, due to the dataset used, it is not relevant in our approach. However, in future work, we can improve this issue since, in spectral clustering, the algorithm learns a robust affinity matrix utilizing several features, allowing us to find optimal weights for each feature simultaneously in Li et al. (2018a). In a variety of applications, spectral clustering has proven to be beneficial in Li et al. (2018b, 2019). In our paper, we use PNN to test the mutual effect of multiple features. Multiple regression (MR) is also used to test the mutual effect of multiple features. To test the mutual effect of the chosen features, multi-class classification can be used like linear discriminant analysis (LDA) which we can use in future work in Yan et al. (2020). A deep learning algorithm is necessary to optimize huge parameters so that the model learns how to extract high-quality features in Ren et al. (2021).

The following is how the rest of the paper is structured: The literature evaluation of various research including citation analysis is detailed in Sect. 2. The dataset, technique, and equations that were utilized are all described in Sect. 3. The findings of the review and discussion are presented in Sect. 4 of the report. In Sect. 5, we talk about our conclusion.

2 Related work

Several studies have been performed to look at the incredible increase in research collaboration during the past decades. The bulk of these is focused on the variables that impact scientific collaboration, which is a field of study led by Melin and Persson (1996), Katz and Martin (1997). Other major but fewer studies, such as Larivière et al. (2014), Jones et al. (2008) and Stewart (1983), have attempted to demonstrate a direct functional relationship between the number of citations gained and specific characteristics of the contributor's list for a scientific article.

The choice to collaborate, particularly with people with different skills, cultures, and experiences, is primarily driven by the intricacy and multidisciplinary nature of certain research issues in He et al. (2009). However, among the predictors of collaboration, there may be elements to examine that are simply 'utilitarian.' This suggests that collaboration is being sought in order to improve the chances of the paper getting published in Kalwij and Smit (2013), accepted by prestigious journals in Al-Herz et al. (2014), or receiving citations (Sin (2011); Leimu et al. (2008)).

Formal help in the form of co-authorship from a well-known and respected scientist can boost the manuscript's credibility significantly. This phenomenon, known as the 'Matthew effect,' was investigated in Robert K. Merton's first research, which demonstrated the 'impact of the cumulative activity,' i.e., scientists with more citations would be cited more frequently than scientists of similar publishing quality. Citation choices are influenced by social factors such as the author's professional position in Merton (1968). Similar reasons might explain why more prestigious institutions have more collaborations than others in Piette and Ross (1992), as well as why more developed countries play a larger role in international cooperation networks in Luukkonen et al. (1992).

Any principal investigator entrusted with creating a collaboration team and, as a result, co-authorship of their work should be aware of the phenomenon. Every co-author has a web of relationships to which they are inexorably tied and which will almost definitely lead to citations. As a result, having more co-authors implies having more social networks, and therefore having a better chance of having co-authored works acknowledged.

Apart from the numerous researches described in the preceding section, many additional empirical investigations have found that co-authorships had better visibility than the average, both in terms of journal importance and citations in Bordons et al. (2013). In Hoekman et al. (2010) Using a sample of papers from 17 demographic journals indexed in the Social Science Citation Index between 1990 and 1992, in Jones et al. (2008). Multi have discovered a potential that the citation has grown by 7%, due to an increase of one author, notwithstanding rare exceptions in certain fields of research (Haslam et al. (2008); Didegah and Thelwall (2013a); Van Dalen et al. (2001, 2005).

They believe that expanding the number of teams increases the division of labor, and hence that the division of scientific activity enhances productivity. According to research in Acedo et al. (2006), co-authorship influences a paper's potential impact on the community of reference, as evidenced by the numerous citations received by the scientific literature surveying managers and organizations.

This is supported by a previous study of the UK and Irish Accounting and Finance category published in 1998–1999 in Beattie and Goodacre (2004). Based on a sample of work published in the top natural journals of science, research in Skilton (2009). examines the critical relevance of 'diversity in the discipline field inside the cooperative team and finds the supremacy of 'intelligent over social' capital in quotation behavior. By analyzing modest changes in the makeup of co-author networks and the articles themselves, researchers have shown how cooperative effects on citations tend to be minimized in Hurley et al. (2013), Didegah and Thelwall (2013b).

Finally, we point out that the connection between author numbers and citations received might be explained in part by the natural increase in self-citation that occurs when works are written by more authors in Leimu and Koricheva (2005). and perhaps from various colleges in Herbertz (1995). According to Larivière et al(2014), self-citation helps to explain the link between impact and collaboration, but it doesn't fully explain it. Rather than a "mechanical" output, this appears to be due to the increased epistemic value associated with collaborative research in (Beaver (2004); Wray (2002)).

3 Dataset and indicators

This section discusses the used dataset and the used methodology.

3.1 Dataset

In this paper, we use Citation Network Dataset from the following link https://www.aminer.cn/citation. The data set is designed for research purposes. The citation data is extracted from DBLP, ACM, MAG (Microsoft Academic Graph), and other sources. The first version contains 629,814 papers and 632,752 citations. Each paper is associated with abstract, authors, year, venue, and title. The data set can be used for clustering with network and side information, studying influence in the citation network, finding the most influential papers, topic modeling analysis, etc. We use DBLP-Citation-network V13: 5,354,309 papers and 48,227,950 citation relationships (2021-05-14). In each text file, each line represents a paper, which is in JSON schema. To make it easier to handle, we convert the dataset into an excel sheet.

3.2 Methodology of impact calculation

To test the impact of co-author count on citation count of research publications, we follow two methods: (i) Pearson’s correlation coefficient (PCC), and (ii) multiple regression (MR).

3.2.1 Pearson’s correlation coefficient (PCC)

Correlation coefficients are used to measure how strong a relationship is between two variables. There are several types of the correlation coefficient, but the most popular is Pearson’s. Pearson’s correlation (also called Pearson’s r) is a correlation coefficient commonly used in linear regression. If you’re starting in statistics, you’ll probably learn about Pearson’s R first. When anyone refers to the correlation coefficient, they are usually talking about Pearson’s.

A correlation coefficient of 1 means that for every positive increase in one variable, there is a positive increase of a fixed proportion in the other. For example, shoe sizes go up in (almost) perfect correlation with foot length. A correlation coefficient of − 1 means that for every positive increase in one variable, there is a negative decrease of a fixed proportion in the other. For example, the amount of gas in a tank decreases in (almost) perfect correlation with speed. Zero means that for every increase, there isn’t a positive or negative increase. The two just aren’t related. One of the most commonly used formulas is Pearson’s correlation coefficient formula. To test the impact of co-author count on citation count of research publications, we calculate Pearson’s correlation coefficient (ra) between the most effective variables and citation count (CC) as following: (i) we calculate ra between the two variables number of authors (NA) and citation count (CC) as shown in Eq. (1). The number of authors variable is derived from the authors.name.

$${\text{ra}} = { }\frac{{n \left( {\sum NA CC} \right) - \left( {\sum NA} \right)\left( {\sum CC} \right)}}{{\sqrt {\left[ {n \sum \left( {NA} \right)^{2} - \left( {\sum NA)^{2} } \right]} \right[n \sum \left( {CC} \right)^{2} - \left( {\sum CC)^{2} } \right]} { }}} .$$
(1)

(ii) We calculate Pearson’s correlation coefficient (rc) between the two variables number of countries (NC) and citation count (CC) as shown in Eq. (2). The number of countries variable is derived from the author.org.

$${\text{rc}} = { }\frac{{n \left( {\sum NC CC} \right) - \left( {\sum NC} \right)\left( {\sum CC} \right)}}{{\sqrt {\left[ {n \sum \left( {NC} \right)^{2} - \left( {\sum NC)^{2} } \right]} \right[n \sum \left( {CC} \right)^{2} - \left( {\sum CC)^{2} } \right]} { }}}.$$
(2)

(iii) We calculate Pearson’s correlation coefficient (rv) between the two variables venue category (VC) and citation count (CC) as shown in Eq. (3). The venue category is derived from the venue.type.

$${\text{rv}} = { }\frac{{n \left( {\sum VC CC} \right) - \left( {\sum VC} \right)\left( {\sum CC} \right)}}{{\sqrt {\left[ {n \sum \left( {VC} \right)^{2} - \left( {\sum VC)^{2} } \right]} \right[n \sum \left( {CC} \right)^{2} - \left( {\sum CC)^{2} } \right]} { }}}.$$
(3)

(iv) We calculate Pearson’s correlation coefficient (ry) between the two variables Year_From (YF) and citation count (CC) as shown in Eq. (4). The Year_From is derived from the year (the published year).

$${\text{ry}} = { }\frac{{n \left( {\sum YF CC} \right) - \left( {\sum YF} \right)\left( {\sum CC} \right)}}{{\sqrt {\left[ {n \sum \left( {YF} \right)^{2} - \left( {\sum YF)^{2} } \right]} \right[n \sum \left( {CC} \right)^{2} - \left( {\sum CC)^{2} } \right]} { }}},$$
(4)

where, ra is Pearson’s correlation coefficient between the two variables NA and CC, rc is Pearson’s correlation coefficient between the two variables NC and CC, rv is Pearson’s correlation coefficient between the two variables VC and CC, ry is Pearson’s correlation coefficient between the two variables YF and CC. NA is the number of authors. NC is the number of Countries. VC is the venue category. CC is the number of citations. YF is the year of publication, n is the number of sample points.

The venue category can be 1, 2 or 3 (Quarter) depending on the venue where the paper has been published in.

3.2.2 Multiple regression (MR)

In the second step, we used multiple regression analysis to investigate the extent to which the citation rates of articles are influenced by the potential factors introduced in Sect. 4.1.

Multiple regression analysis using four factors as explanatory variables showed that the highly significant explanatory variables were as follows (in decreasing order of partial correlation coefficient): (i) number of authors (NA), (ii) number of countries (NC), (iii) venue category (VC), (iv) Years_From (YF). formula and calculation of multiple linear regression represented in (5).

$${\text{NCC}} = {\upbeta }0 + {\upbeta }1\left( {{\text{NA}}} \right) + {\upbeta }2{ }\left( {{\text{NC}}} \right) + {\upbeta }3{}\left( {{\text{VC}}} \right) + {\upbeta }4\left( {{\text{YF}}}\right) + \EUR,$$
(5)

where NCC is the new citation count (the predicted value of citation count), Β0 is the NCC-intercept (constant value), β1 is the change in NCC each 1 increment change in NA, β2 is the change in NCC each 1 increment change in NC, β3 is the change in NCC each 1 increment change in VC, β4 is the change in NCC each 1 increment change in YF, € is the model error term.

The most common attributes that considered as factors potentially affecting the citation frequency of the sample articles are summarized as shown in Table 1.

Table 1 Attributes affecting citation frequency
Full size table

3.3 Effective prediction module (EPM)

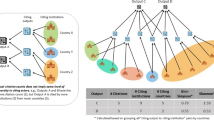
To predict the number of citations from the previously mentioned factors (NA, NC, VC, and YF), we use Probabilistic Neural Network (PNN). EPM is used to predict the citation count based on the most effective factors chosen in Sect. 4.2.1 which are: (i) NA, (ii) NC, (iii) VC. The EPM uses the PNN to predict the citation count, using the most effective factors chosen in Sect. 4.2.1 which are: (i) NA, (ii) NC, (iii) VC. In order to detect the citation count (CC), PNN is trained using the training dataset.

Then PNN will be tested using the testing dataset. The architecture of PNN is shown in Figs. 1 and 2. The steps of the PNN based prediction algorithm (PPA) are shown in Algorithm 1.

Fig. 1
figure 1

PNN

Full size image
Fig. 2
figure 2

PNN architecture

Full size image

3.3.1 Illustrative example

Assume there are ten cases. For each case, we consider the values from three factors NA, NC, and VC as shown in Table 2.

Table 2 Predictors (NA, NC, VC)
Full size table

Assume new predictors with values [4, 3, 1]. Count_1 is the number of examples belongs to CC = 1. Count_2 is the number of examples belongs to CC = 2. Count_3 is the number of examples belongs to CC = 3.

As P2 has the largest value, the new predictors with values [4, 3, 1] will be detected as CC = 2 (Tables 2, 3, 4, 5, 6).

Table 3 Input data set for PNN
Full size table
Table 4 Test example
Full size table
Table 5 Training calculations 1
Full size table
Table 6 Training calculations 2
Full size table

4 Implementation and evaluation

This section presents the results of the methodology presented in Sect. 4, which was carried out to investigate how co-author count impacts the citations of the research publications.

4.1 Calculating the Pearson’s correlation coefficient (PCC)

In order to investigate the impact of co-author count on citation count of research publications, we calculate Pearson’s correlation coefficient (ra) between the two variables number of authors (NA) and citation count (CC) as shown in Fig. 3.

Fig. 3
figure 3

No. of citation count vs. no. of authors (NA)

Full size image

From Fig. 3, it is shown that there is a strong relationship between the Number of Authors (NA) and Citation Count (CC). The ra =  + 0.0539 (positive correlation) means that both variables move in tandem—that is, in the same direction. When NA increases, CC increases. When NA decreases, CC decreases. We also calculate Pearson’s correlation coefficient between the citation count (CC) and the most effective variables to compare between the impact of the number of authors and the impact of the other factors such as (i) rc between number of countries (NC) and citation count (CC) as shown in Fig. 4.

Fig. 4
figure 4

No. of citation count vs. no. of countries (NC)

Full size image

From Fig. 4, it is shown that there is a positive relationship between the number of countries (NC) and citation count (CC). The rc =  + 0.0355 (positive correlation) means that both variables move in tandem—that is, in the same direction. When NA increases, CC increases. When NA decreases, CC decreases. (ii) rv between Venue Category (VC) and Citation Count (CC) as shown in Fig. 5.

Fig. 5
figure 5

No. of citation count vs. venue category (VC)

Full size image

From Fig. 5, it is shown that there is a negative relationship (inverse correlation) between venue category (VC) and citation count (CC). The rv = − 0.1176 which makes sense as VC = 1, 2, or 3. Then number indicates the quarter (Q). When the number of Q increases, the impact factor of the journal decreases, and it makes sense that when the impact decreases (the Q increases), the citation count decreases. (iii) ry between Year_From (YF) and citation count (CC) as shown in Fig. 6.

Fig. 6
figure 6

No. of citation count vs. Year_From (YF)

Full size image

From Fig. 6, it is shown that there is a negative relationship (inverse correlation) between Year_From (YF) and citation count (CC). The ry = − 0.0264. The older the search, the higher the number of citation count (CC). The whole calculated PCC (r) values are shown in Table 7.

Table 7 Impact of selected factors (NA, NC, VC, and YF) on CC
Full size table

From Table 7, it is shown that the NA is the most influential factor (the relation between NA and CC is the most powerful relation).

4.2 Calculating the multiple regression (MR)

In order to predict the number of citations from the previously mentioned factors (NA, NC, VC, and YF), we use Multiple Linear Regression (MLR). The goal of multiple linear regression (MLR) is to model the linear relationship between the explanatory (independent) variables and response (dependent) variables. The higher R-square, the tight relationship exists between dependent variables and independent variables. In the case of using all the previous factors (NA, NC, VC, and YF), the R-square = 0.00516. The equation from the data analysis should be NCC = 8.664 + 0.5709 × NA − 0.1372 × NC + 0.139 × VC − 0.0526 × YF. The normal probability plot is shown in Fig. 7.

Fig. 7
figure 7

Normal probability plot (NA,NC,VC,YF)

Full size image

From Fig. 7, it is shown that the residuals are normally distributed. In the case of removing one factor (NA) and using only the three factors (NC, VC, and YF), the R-square = 0.00243. The equation from the data analysis should be NCC = 8.8806 + 0.4947 × NC − 0.0728 × VC − 0.0355 × YF. The normal probability plot is shown in Fig. 8. It is observed that the R-square decreases in case of removing NA as shown in Table 8 which means that the NA is the most influential factor (the relation between NA and CC is the most powerful relation).

Fig. 8
figure 8

Normal probability plot (NC,VC,YF)

Full size image
Table 8 MLR calculations
Full size table

4.3 Results of effective prediction module (EPM)

To test the effect in the case of implementing PNN, we first partition the used dataset into a training dataset and testing dataset, and then we implement back propagation (BP), general regression neural network (GRNN), and PNN. The values of mean and standard deviation are shown in Table 9.

Table 9 Accuracy of BP, GRNN, and PNN
Full size table

The results have proven that PNN has the best prediction accuracy.