Skip to main content
SpringerLink
Log in

Heat transfer in a non-uniform channel on MHD peristaltic flow of a fractional Jeffrey model via porous medium

  • Original Paper
  • Published:
Indian Journal of Physics Aims and scope Submit manuscript

Abstract

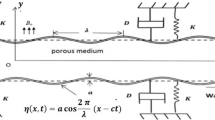
Peristalsis has recently been a hot topic in biomedical engineering and biological sciences because of its importance. This paper provides a rudimentary insight into the peristaltic transport of an MHD fractional fluid over a permeable medium in a non-uniform channel that is the aim of the research. In mathematical modeling, fluid fills the porous region according to an altered Darcy's law. The derived equations were solved analytically via the long-wavelength hypothesis reliant on the small Reynolds number hypothesis, to solve the leading equations. Temperature, velocity, pressure gradient, friction forces, and pressure rise are all solved using confined solutions. The obtained results were validated with the state-of-threat literature reports. It was claimed that our systematic approach. The numerical results are computed, discussed numerically, and graphs are used to present them. The effects of relevant parameters on the previously mentioned quantities are investigated by plotting graphs based on the computational results. The results show that the parameter effect is extremely powerful. As a limiting case of the problem considered, an adequate comparison with prior results in the literature has been made.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

Data availability

The manuscript has no associated data.

References

  1. T W Latham. M I T (1966)

  2. N S Wahid, M E H Hafidz Uddin, N M Arifin, M Turkyilmazogl and N A Abd Rahmin C F D Lett. 12 1 (2020)

    Google Scholar 

  3. J K Singh and S Vishwanath Int J Thermofluid Sci Technol. 7 07040 (2020)

    Article  Google Scholar 

  4. J Zhao Chin. J. Phys. 67 501 (2020)

    Article  Google Scholar 

  5. H Rachid. Abstr Appl Anal. 2015 (2015)

  6. H Qi and H Jin Acta Mech. Sin. 22 301 (2006)

    Article  ADS  Google Scholar 

  7. S Amana and Q Al-Mdallala J. King Saud Univ. Sci. 32 450 (2020)

    Article  Google Scholar 

  8. A M Abd-Alla, S M Abo-Dahab, E N Thabet and M A Abdelhafez Sci. Rep. 12 10608 (2022)

    Article  ADS  Google Scholar 

  9. Y Carrera, G Avila-de, E J la Rosa and J Alvarez-Ramirez Vernon-Carter Phys. A: Stat. Mech. Appl. 482 276 (2017)

    Article  Google Scholar 

  10. X Guo, J Zhou, H Xie and Z Jiang Math Probl Eng. 2018 1 (2018)

    Google Scholar 

  11. A M Abd-Alla, E N Thabet and F S Bayones Sci. Rep 12 3348 (2022)

    Article  ADS  Google Scholar 

  12. V K Narla, K M Prasad and J V Ramanamurthy Chin J Eng. 2013 1–7 (2013)

    Article  Google Scholar 

  13. A Razzaq, A R Seadawy and N Raza Physics Scr. 95 11 115220 (2020)

    Article  ADS  Google Scholar 

  14. K Javid, S Ud-Din Khan, S Ud-Din Khan, M Hassan, A Khan and S A Alharbi Eur Phys J Plus 136 1 (2021)

    Google Scholar 

  15. Z Khanet al. Coat 10 163 (2020)

    Article  Google Scholar 

  16. K Javid, U F Alqsair, M Hassan, M M Bhatti, T Ahmad and E Bobescu Biomech Model Mechanobiol. 20 1399 (2021)

    Article  Google Scholar 

  17. F S Bayones, A M Abd-Alla and E N Thabet Waves in Random and Complex Media (2022). https://doi.org/10.1080/17455030.2021.2019352

    Article  Google Scholar 

  18. K Ramesh, D Tripathib, M M Bhatti and C M Khalique J. Mol. Liq. 314 113568 (2020)

    Article  Google Scholar 

  19. A M Abd-Alla and S M Abo-Dahab Multidiscip Model Mater Struct 17 895 (2021). https://doi.org/10.1108/MMMS-12-2020-0292

    Article  Google Scholar 

  20. M Rahimi-Gorji, S Cosyns, C Debbaut, G Ghorbaniasl, W Willaert and W Ceelen Eur J Surg Oncol. (2022). https://doi.org/10.1016/j.ejso.2021.12.317

    Article  Google Scholar 

  21. F S Bayones, A M Abd-Alla and E N Thabet Complexity (2021). https://doi.org/10.1155/2021/9911820

    Article  Google Scholar 

  22. T Hayat, M Javed and N Ali Transp. Porous Media 74 259 (2008)

    Article  MathSciNet  Google Scholar 

  23. E U Haque, A U Awan, N Raza, M Abdullah and M A Chaudhry Alex. Eng. J. 57 2601 (2018)

    Article  Google Scholar 

  24. A M Abd-Alla, S M Abo-Dahab, E N Thabet, M A Abdelhafez and E N Thabet Waves in Random and Complex Media (2022). https://doi.org/10.1080/17455030.2022.2084653

    Article  Google Scholar 

  25. M Hameed, A Khan, R Ellahi and M Raza Eng Sci Technol an Int J Eng Sci Technol. 18 496 (2015). https://doi.org/10.1016/j.jestch.2015.03.004

    Article  Google Scholar 

  26. M Rahimi-Gorji, C Debbaut, G Ghorbaniasl, S Cosyns, W Willaert and W Ceelen Sci Rep. 12 6305 (2022). https://doi.org/10.1038/s41598-022-10369-8

    Article  ADS  Google Scholar 

  27. M Kothandapani and S Srinivas Phys. Lett. 372 4586 (2008)

    Article  Google Scholar 

  28. K Vajravelu, G Radhakrishnamacharya and S V Radha Krishnamurty Int J Non Linear Mech. 42 754 (2007)

    Article  Google Scholar 

  29. M Rahimi-Gorji, C Debbaut, G Ghorbaniasl, W Willaert, S Cosyns and W Ceelen Eur J Surg Oncol. (2021). https://doi.org/10.1016/j.ejso.2020.11.222

    Article  Google Scholar 

  30. T Anwar, P Kumam, A Tassaddiq, I Khan and P Thounthong Chin. J. Eng. 68 849 (2020)

    Google Scholar 

  31. M Rahimi-Gorji et al. Eur J Surg Oncol. 28 S110 (2021). https://doi.org/10.1245/s10434-021-09682-9

    Article  Google Scholar 

  32. F Ali, S Majeed and A Imtiaz Math. Probl. Eng. 2021 6624912 (2020). https://doi.org/10.1155/2021/6624912

    Article  Google Scholar 

  33. M Rahimi-Gorji, C Debbaut, W Willaert, P. Segers, G Ghorbaniasl, W Ceelen. Biomed. Eng. (2019). http://hdl.handle.net/1854/LU-8638305

  34. S Liu, W Yang and L Zheng Appl. Math. Lett. 124 107630 (2022)

    Article  Google Scholar 

Download references

Acknowledgements

The authors are grateful for the financial support provided by Taif University Researchers Supporting Project (TURSP-2020/96), Taif University, Taif, Saudi Arabia.

Author information

Authors and Affiliations

  1. Department of Mathematics, Faculty of Science, Sohag University, Sohag, Egypt

    A. M. Abd-Alla & Esraa N. Thabet

  2. Department of Mathematics, Faculty of Science, Aswan University, Aswan, 81528, Egypt

    Esraa N. Thabet

  3. Department of Mathematics and Statistics, College of Science, Taif University, P. O. Box 11099, Taif, 21944, Saudi Arabia

    F. S. Bayones & Abdullah M. Alsharif

Authors
  1. A. M. Abd-Alla
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Esraa N. Thabet
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. F. S. Bayones
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Abdullah M. Alsharif
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Esraa N. Thabet.

Ethics declarations

Conflict of interest

The authors have no relevant financial or non-financial interests to disclose. The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix I

Appendix I

$$ k = \frac{ - \beta }{{1 + R}},\;\;f_{1} = \left( {1 + \lambda_{1}^{{\alpha_{1} }} \partial_{t}^{{\alpha_{1} }} } \right)\,,\,\,\,\,\,\,\,\,\,\,f_{2} = \,\,\left( {1 + \lambda_{1}^{{\beta_{1} }} \partial_{t}^{{\beta_{1} }} } \right), $$
$$ c_{1} = \frac{ - 1}{{2\left( {h + \gamma } \right)}},\;\;c_{2} = \frac{{\left( {1 - kh\left( {2\gamma + h} \right)} \right)}}{2},\;\;A = f_{2} + f_{1} M^{2} K, $$
$$ a_{1} = \frac{{e^{{\frac{ - \sqrt A y}{{\sqrt K \sqrt {f_{2} } }}}} }}{{2\left( {1 + e^{{\frac{2h\sqrt A }{{\sqrt K \sqrt {f_{2} } }}}} } \right)A^{{{\raise0.7ex\hbox{$5$} \!\mathord{\left/ {\vphantom {5 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} }}, $$
$$ a_{2} = e^{{\frac{2h\sqrt A y}{{\sqrt K \sqrt {f_{2} } }}}} \sqrt {f_{2} } \sqrt K - e^{{\frac{2\sqrt A y}{{\sqrt K \sqrt {f_{2} } }}}} \sqrt {f_{2} } \sqrt K - e^{{\frac{h\sqrt A y}{{\sqrt K \sqrt {f_{2} } }}}} h\sqrt A , $$
$$ a_{3} = - e^{{\frac{{\sqrt A \left( {h + 2y} \right)}}{{\sqrt K \sqrt {f_{2} } }}}} h\sqrt A + e^{{\frac{\sqrt A y}{{\sqrt K \sqrt {f_{2} } }}}} y\sqrt A + e^{{\frac{{\sqrt A \left( {2h + y} \right)}}{{\sqrt K \sqrt {f_{2} } }}}} y\sqrt A , $$
$$ \begin{gathered} a_{4} = e^{{\frac{\sqrt A h}{{\sqrt K \sqrt {f_{2} } }}}} \left( {2f_{2}^{2} - f_{1} f_{2} K\left( { - 2\frac{dp}{{dx}} + 2c_{2} Gr + kGr\left( {h^{2} + 2K} \right) - 4M^{2} } \right) + f_{1}^{2} K^{2} M^{2} \left( {2\frac{dp}{{dx}} - 2c_{2} Gr - kGrh^{2} + 2M^{2} } \right)} \right), \hfill \\ a_{5} = e^{{\frac{{\sqrt A \left( {h + 2y} \right)}}{{\sqrt K \sqrt {f_{2} } }}}} \left( {2f_{2}^{2} - f_{1} f_{2} K\left( { - 2\frac{dp}{{dx}} + 2c_{2} Gr + kGr\left( {h^{2} + 2K} \right) - 4M^{2} } \right) + f_{1}^{2} K^{2} M^{2} \left( {2\frac{dp}{{dx}} - 2c_{2} Gr - kGrh^{2} + 2M^{2} } \right)} \right), \hfill \\ a_{6} = e^{{\frac{\sqrt A y}{{\sqrt K \sqrt {f_{2} } }}}} \left( { - 2f_{2}^{2} + f_{1}^{2} K^{2} M^{2} \left( { - 2\left( {\frac{dp}{{dx}} - 2c_{2} Gr + M^{2} } \right) + kGry^{2} } \right) + f_{1} f_{2} K\left( { - \frac{dp}{{dx}} + 2c_{2} Gr - 4M^{2} + kGr\left( {2K + y^{2} } \right)} \right)} \right), \hfill \\ a_{7} = e^{{\frac{{\sqrt A \left( {2h + y} \right)}}{{\sqrt K \sqrt {f_{2} } }}}} \left( { - 2f_{2}^{2} + f_{1}^{2} K^{2} M^{2} \left( { - 2\left( {\frac{dp}{{dx}} - 2c_{2} Gr + M^{2} } \right) + kGry^{2} } \right) + f_{1} f_{2} K\left( { - \frac{dp}{{dx}} + 2c_{2} Gr - 4M^{2} + kGr\left( {2K + y^{2} } \right)} \right)} \right), \hfill \\ \end{gathered} $$
$$ b_{1} = 2\left( {1 + e^{{\frac{2h\sqrt A }{{\sqrt K \sqrt {f_{2} } }}}} } \right)A^{{{\raise0.7ex\hbox{$5$} \!\mathord{\left/ {\vphantom {5 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} , $$
$$ b_{2} = - 2\left( {1 - e^{{\frac{2h\sqrt A }{{\sqrt K \sqrt {f_{2} } }}}} } \right)f_{1} f_{2}^{{{\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} K^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} + 2\left( { - 1 - e^{{\frac{2h\sqrt A }{{\sqrt K \sqrt {f_{2} } }}}} } \right)f_{1}^{2} \sqrt {f_{2} } K^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-\nulldelimiterspace} 2}}} M^{2} , $$
$$ b_{3} = 2\left( { - 1 - e^{{\frac{2h\sqrt A }{{\sqrt K \sqrt {f_{2} } }}}} } \right)f_{1}^{2} hK^{2} M^{2} \sqrt A , $$
$$ b_{4} = - 4e^{{\frac{2h\sqrt A }{{\sqrt K \sqrt {f_{2} } }}}} f_{1} f_{2} hK\sqrt A \cosh \left( {\frac{h\sqrt A }{{\sqrt K \sqrt {f_{2} } }}} \right), $$
$$ b_{5} = - 2\left( { - 1 - e^{{\frac{2h\sqrt A }{{\sqrt K \sqrt {f_{2} } }}}} } \right)f_{2}^{{{\raise0.7ex\hbox{$5$} \!\mathord{\left/ {\vphantom {5 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} \sqrt K + \left( {1 - e^{{\frac{2h\sqrt A }{{\sqrt K \sqrt {f_{2} } }}}} } \right)f_{1} f_{2}^{{{\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} GrK^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} \left( {2c_{2} + c_{1} h + kh^{2} + 2kK} \right), $$
$$ b_{6} = - 4\left( { - 1 - e^{{\frac{2h\sqrt A }{{\sqrt K \sqrt {f_{2} } }}}} } \right)f_{1} f_{2}^{{{\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} K^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} M^{2} - 2c_{2} \left( { - 1 + e^{{\frac{2h\sqrt A }{{\sqrt K \sqrt {f_{2} } }}}} } \right)f_{1}^{2} \sqrt {f_{2} } GrK^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} M^{2} , $$
$$ b_{7} = \left( { - 1 + e^{{\frac{2h\sqrt A }{{\sqrt K \sqrt {f_{2} } }}}} } \right)f_{1}^{2} \sqrt {f_{2} } Grh\left( {2c_{1} + kh} \right)K^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} M^{2} + 2\left( { - 1 + e^{{\frac{2h\sqrt A }{{\sqrt K \sqrt {f_{2} } }}}} } \right)f_{1}^{2} \sqrt {f_{2} } K^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-\nulldelimiterspace} 2}}} M^{4} , $$
$$ b_{8} = - 2\left( {1 + e^{{\frac{2h\sqrt A }{{\sqrt K \sqrt {f_{2} } }}}} } \right)f_{2}^{2} \sqrt A h - 4c_{1} e^{{\frac{h\sqrt A }{{\sqrt K \sqrt {f_{2} } }}}} f_{1} f_{2} GrK^{2} \sqrt A - 2c_{2} \left( { - 1 - e^{{\frac{2h\sqrt A }{{\sqrt K \sqrt {f_{2} } }}}} } \right)f_{1}^{2} GrK^{2} M^{2} \sqrt A , $$
$$ \begin{gathered} b_{9} = - \frac{1}{3}\left( { - 1 - e^{{\frac{2h\sqrt A }{{\sqrt K \sqrt {f_{2} } }}}} } \right)f_{1}^{2} Grh^{2} \left( {3c_{1} + kh} \right)K^{2} M^{2} \sqrt A + 2\left( { - 1 - e^{{\frac{2h\sqrt A }{{\sqrt K \sqrt {f_{2} } }}}} } \right)f_{1}^{2} hK^{2} M^{4} \sqrt A + \hfill \\ \,\,\,\,\,\,\,\,\,\,\frac{1}{3}e^{{\frac{h\sqrt A }{{\sqrt K \sqrt {f_{2} } }}}} f_{1} f_{2} Grh\left( {6c_{2} + 3c_{1} h + kh^{2} } \right)K\sqrt A \cosh \left( {\frac{h\sqrt A }{{\sqrt K \sqrt {f_{2} } }}} \right), \hfill \\ \end{gathered} $$
$$ b_{10} = 4e^{{\frac{h\sqrt A }{{\sqrt K \sqrt {f_{2} } }}}} f_{1} f_{2} Gr\left( {c_{1} + kh} \right)K^{2} \sqrt A \cosh \left( {\frac{h\sqrt A }{{\sqrt K \sqrt {f_{2} } }}} \right) - 8e^{{\frac{h\sqrt A }{{\sqrt K \sqrt {f_{2} } }}}} f_{1} f_{2} hKM^{2} \sqrt A \cosh \left( {\frac{h\sqrt A }{{\sqrt K \sqrt {f_{2} } }}} \right). $$

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Abd-Alla, A.M., Thabet, E.N., Bayones, F.S. et al. Heat transfer in a non-uniform channel on MHD peristaltic flow of a fractional Jeffrey model via porous medium. Indian J Phys 97, 1799–1809 (2023). https://doi.org/10.1007/s12648-022-02554-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12648-022-02554-2

Keywords

Search

Navigation