Modelling and simulation of atmosphere-breathing electric propulsion intakes via direct simulation Monte Carlo

Abstract

The Air-Breathing Ion Engine (ABIE) is an electric propulsion system capable of compensating for drag at low altitudes by ingesting the surrounding atmospheric particles to be utilized as propellant. The current state of the art of the ABIE performance is evaluated via Direct Simulation Monte Carlo (DSMC), due to the rarefied nature of the atmosphere in Very-Low Earth Orbit (VLEO). Nevertheless, the scarce availability of relevant simulation methodologies in the literature limits the repeatability of such numerical studies. Therefore, this paper proposes an independent methodology applicable to the modelling and simulation of Atmosphere-Breathing Electric Propulsion (ABEP) intakes that aims to validate the ABIE DSMC results retrieved from the literature. This is achieved by investigating the ABIE intake collection efficiency and compression ratio through the open-source solver dsmcFoam+ and by assessing the results against the available RARAC-3D DSMC data. First, the variation of grid transparency is discussed and compared between both solvers, yielding a mean percentage error of $2.97\%$ for the compression ratio and $2.06\%$ for the collection efficiency. Second, the absence of intermolecular collisions is verified for which errors of $1.61\%$ for collection efficiency and $3.49\%$ for compression ratio are observed. Then, the variation of flow incidence angle is simulated between $0^{\circ }$ and $15^{\circ }$, yielding differences lower than $1.80\%$. Consecutively, the intake aspect ratio is varied between 10 and 40, for which a maximum discrepancy of $1.83\%$ is measured and, finally, the drag coefficient of the intake is obtained in dsmcFoam+ to define the power density requirements.

1 Introduction

Because of their proximity to Earth, missions in Very-Low Earth Orbit (VLEO: 100-450 km) benefit from several payload and platform advantages. The performance of such missions is improved as the distance with the ground decreases when compared to higher orbits. For instance, as the diffraction of an imaging system is proportional to the orbital altitude and its corresponding radiometric resolution is inversely proportional to the square distance from the target, the performance of optical payloads results enhanced at lower altitudes. Similarly for the case of synthetic aperture radar payloads, the signal return is also improved as the required antenna area is inversely proportional to the altitude. Moreover, the requirements for accuracy of measured signals and transmittance power in data communications are reduced, meaning that smaller on-board antennas may be used to achieve the same performance as higher altitudes. Alternatively, should the improved payload performance not be dictated by the mission requirements, the on board sensors and antennas may be re-sized to achieve the intended outcome at a reduced payload volume and weight, hence improving the launch capabilities. This would lead to an increase in available launch mass with the same propellant, or, alternatively, to a lower launch cost for the same payload mass [8].

In addition to the launch capabilities, which are affected directly by flying to lower orbits in VLEO, missions operating within this range require no end-of-life manoeuvre for disposal to comply with the Inter-Agency Space Debris Coordination Committee (IADC) guidelines. Because of the atmospheric drag present at low altitudes, re-entry is naturally guaranteed. This same reason lowers the risk of collision with space debris, which have a shorter residence time in the lower region of the atmosphere [10]. Furthermore, the persisting atmospheric layer of the atmosphere shields solar activity effects in VLEO, hence extending the lifetime of the sensitive electronics on-board the S/C. A more dedicated review and analysis of these benefits is retrievable from [5].

As a consequence of the numerous advantages offered, the VLEO range is critically important for high-resolution imaging, weather forecasting, surveillance services, communications, precision agriculture, earth observation and many more space applications. Nevertheless, due to the presence of a residual atmosphere at such altitudes, the impacts between an atmospheric particle and the S/C generates an exchange of energy which heats up, slows down the S/C and leads to orbital decay. The mission lifetime is a mission design driver limited by the amount of drag that the propulsion system can compensate for and by its sustainable time duration. These two parameters depend on the drag the S/C generates, the amount of propellant it can store on-board, and the propulsion system efficiency [19]. Moreover, increasing the on board propellant not only would increase the mass of the satellite, and therefore the overall mission cost, but would also enlarge the dimensions of the S/C, leading to higher levels of drag.

In recent years, substantial progress has been made on mission enhancement in VLEO owing to the advancement of Atmosphere-Breathing Electric Propulsion (ABEP). The innovative concept of ABEP is based on the ingestion of atmospheric particles to be used as propellant. ABEP systems typically comprise of two main components: the intake, whose function is to collect the scarce atmospheric molecules, and the thruster, which ionizes, accelerates, and expels the particles in the opposite direction to the S/C velocity vector, thereby generating thrust through momentum exchange [19]. A schematic of the overall system applied to a generic spacecraft is shown in Fig. 1, where the intake is facing into the direction of flight, and the thruster powered by the solar arrays is located inside the S/C core.

Fig. 1

Schematic of ABEP concept; adapted from [8]

The concept offers a flexible solution to the propellant restriction as the need for propellant storage is partially or entirely eliminated, virtually enabling continuous operations within VLEO. Hence, the limiting factor is not the depletion of propellant but the deterioration of other main subsystems [19].

Drawing from the countless opportunities enabled by ABEP, this paper aims to contribute to the research community involved in the development of such technologies by proposing a reproducible methodology for modelling and simulating the performance of ABEP intakes via Direct Simulation Monte Carlo (DSMC). In fact, both the scarce availability of replicable methodologies for numerical analysis retrievable from the literature and the closed source nature of the solvers employed, constrain the degree of reproducibility of the research method, and therefore its overall validity. Hence, the simulation methodology described in this paper is developed within the dsmcFoam+ framework, a free and open source software, that is applicable to any passive ABEP intake by varying the corresponding operational constraints, intake geometry and environmental conditions. For the purpose of this research, the design developed by Fujita [6, 7], Hisamoto [9] and Nishiyama [12] of the Japan Aerospace Exploration Agency (JAXA) is investigated such that the results obtained in dsmcFoam+ can be compared and validated with those retrieved from the literature.

1.1 Air-breathing ion engine

The first ABEP design was proposed in 2003 under the name of Air-Breathing Ion Engine (ABIE) and is still considered one of the most advanced concepts in the context of ABEP [12]. The system configuration shown in Fig. 2 is composed of an air intake, a discharge chamber in which the collected atmosphere particles are ionized actively by an Electron Cyclotron Resonance (ECR) ion engine and a neutralizer.

Fig. 2

Operation principle of ABIE, with no neutralizer [12]

As opposed to other ABEP concepts, the intake is fully integrated around the S/C cylindrical core and it entails two main sections: a collimator and a reflector, or diffuser. The former presents numerous slender ducts, resembling the shape of straws - in a honeycomb structure - to form narrow passages. The main function of this section is to reduce the backflow of the discharged particles. The reflector, on the other hand, dams up the flow and reflects the particles in both the mirror direction as well as a random direction at lower velocity values. This, in fact, is a 45$^{\circ }$ surface at the back of the intake. The concept also includes grids for ion beam acceleration at the outlet of the intake, which have a transparency of about 25%. Nishiyama [12] then conducted a preliminary sizing of ABIE and determined the cross-sectional cylindrical area of the inlet for a varying design altitude of 150–200 km.

In 2004, Fujita [6] developed the ABIE concept and integrated the intake within the ideal S/C configuration, comprising of solar panels to provide sufficient power to the thruster and aerodynamic surfaces for attitude control, as shown in Fig. 3.

Fig. 3

Conceptual diagram of fully-integrated ABIE [7]

The concept was then simulated through the RARAC-3D DSMC model such that the geometrical dimensions of the intake could be optimised. In particular, it is important to observe the variation of the core dimensions as a function of altitude in Fig. 4; when ABIE is designed for 140 km (a), the length is 0.8 m and the outer inlet diameter is 1.16 m. Conversely, for a design altitude of 200 km (b), the length increases to 2.91 m and inlet diameter increases to 1.29 m due to the scarcer presence of air particles [7].

Fig. 4

Optimised ABIE intake dimensions for an altitude of a 140 km and b 200 km [7]

A final study from a 2012 paper [9] published by JAXA further investigates the performance of the ABIE concept via the RARAC-3D code. In addition to the varying intake aspect ratio, the effect of incidence angle was investigated. The main design of the ion engine has been kept constant throughout the years, with the major modification of having removed the straws in the inlet region for the simulations. The results of these publications set the basis for the work of this research and are hereby used to validate the accuracy of the methodology developed over the following sections.

1.2 Air intake

The most important component in the ABIE concept for the purpose of this paper is the air intake. Its function is to scoop the rarefied atmosphere particles and to feed them into the discharge chamber while minimising the backflow and corresponding flow losses. The design of the ABIE intake is non-trivial due to the flow conditions experienced in VLEO. The Knudsen Number Kn, defined in Eq. 1 as the ratio of the mean free path of the molecules $\lambda$ to the characteristic length of the S/C, results large (i.e. $Kn>>10$).

$$\begin{aligned} Kn=\lambda /L \end{aligned}$$

(1)

The flow regime is thus considered as Free Molecular Flow (FMF), meaning that the probability of intermolecular collisions is very low, and the flow is dominated by collisions at the walls. Moreover, the reflection behaviour of such collisions in VLEO has been shown to be effectively diffuse due to current typical spacecraft materials via numerical models and in-flight measurements of the S3-1, Proton 2, Ariel 2 and Explorer 6 satellites [11]. This explains the cylindrical geometry chosen for the satellite core which aims to suppress the scattering of the inflowing particles as much as possible.

The two most important parameters employed in this paper to evaluate the performance of the air intake are the compression ratio $\beta$ and intake collection efficiency $\eta _{c}$. Ideally, both should be maximised to achieve the highest performance. However, as discussed in this paper, a compromise between the two often must be made. The first variable is defined in Eq. 2 as the ratio of the atmospheric density reached inside the chamber $\rho _{c}$ to its free stream equivalent $\rho$:

$$\begin{aligned} \beta =\rho _{c}/\rho \end{aligned}$$

(2)

The second parameter is defined in Eq. 3 and it represents the number of particles that reach the thruster $N_{thr}$, divided by the number of incoming flow particles $N_{in}$:

$$\begin{aligned} \eta _{c}=N_{thr}/N_{in} \end{aligned}$$

(3)

To perform DSMC simulations on the intake, the geometrical model in Fig. 5 is implemented.

Fig. 5

Geometrical model for the ABIE air intake [6]

The inner cylinder represents the satellite core and has a radius $R_1$ and length $L_1$, whereas the outer cylinder forms the air duct with a radius $R_2$ and length $L_1+L_2$. The convergence angle of the reflector is kept at 45$^{\circ }$ such that the captured air particles reflect towards the discharge chamber. The entrance to the latter is represented with a circular plate of radius $R_3$ at the back of the intake. In the case of the ABIE intake, this back plate constitutes the acceleration grid required by the ion engine. However, for the simulation of different intakes the grid can be adjusted to the design criteria.

To investigate and discuss the effect of varying intake aspect ratios, the dimensionless geometrical parameter X is introduced in Eq. 4 as defined by Fujita [7], for which the intake geometries can be easily varied.

$$\begin{aligned} X=(R_2-R_1)/L_1 \end{aligned}$$

(4)

Table 1 Geometrical dimensions of the ABIE air intake [6]

The geometrical dimensions reported in Table 1 are employed to reproduce the DSMC investigation carried out by Fujita [7]. It is important to note that the dimensions of the S/C core are kept constant while the inlet outer radius $R_2$ is varied, such that the aspect ratio may be varied. Computer-Aided Design (CAD) models are thus generated and shown in Fig. 6. The effect of an increase in X is evident as the overall air duct volume is reduced. While this may allow fewer particles to enter the intake, further compression is expected.

Fig. 6

CAD models of the air intake with increasing aspect ratio X

In addition to the geometry of the air intake, it is also important to determine the environmental conditions surrounding the S/C. Quantifying accurately the properties of the Earth’s atmosphere is rather challenging as the environment is a complex dynamic system that is constantly changing over space and time. Given the elaborate nature of the atmosphere, a reference atmospheric model is required to describe how the properties of ideal gases change, primarily as a function of altitude. Due to the large number of factors that continuously influence the real atmosphere, such as latitude and day of the year, a reference is agreed internationally for the model to be representative of year-round and midlatitude conditions. Throughout the work of this paper, the representative values reported by Fujita [7] for an altitude of 180 km are used as a reference. It is worth noticing that the three main species detected at this altitude are diatomic Nitrogen $N_2$, diatomic Oxygen $O_2$ and monoatomic Oxygen O, and their corresponding number density n, average molecular weight $\overline{M_w}$, velocity v and temperature T are reported in Table 2. These are obtained through the MSISE-90 (Mass Spectrometer-Incoherent Scatter Model) atmospheric model for a latitude and longitude of 0$^{\circ }$. The model is also initiated on the $1^{st}$ of January 2002 as a characteristic representation of the upper atmosphere [7].

Table 2 Atmospheric conditions at 180 km; MSISE-90 [7]

2 Direct simulation Monte Carlo

As opposed to the differential equations in continuum mechanics, the DSMC method measures directly the physical action of individual simulated particles. A large representative number of simulated molecules is required in order for the global distribution function of the real gas to be fully discretised, although this number should always be much smaller than the real number of particles [14]. It follows that each DSMC particle may represent several real particles. The molecules move in a simulated physical space such that time t is a parameter and the flow is computed as unsteady. This physical space is referred to as the computational domain, which is split into many cells of side length $\varDelta x$. In a small time step $\varDelta t$, the molecular motion and the intermolecular collisions are decoupled, where the time steps must be much smaller than the local mean collision time. The simulator therefore calculates and stores the cartesian positions, velocities and internal energies of each molecule as they change with molecular collisions and boundary interactions [3]. Because the DSMC method is inherently stochastic, the physical quantities of interest are computed as averages of single instantaneous fluctuating values over the converged computational time [1].

The DSMC solver for rarefied gas dynamics adopted for the work of this paper is dsmcFoam+. It is a package within the OpenFOAM (Open-source Field Operation And Manipulation) software framework and parallelised with Message Passing Interface (MPI). The toolbox, developed in C++, is open-source and released under the General Public License (GNU), as published by the Free Software Foundation. dsmcFoam+ is an extension of the standard dsmcFoam solver, and it includes several key features for both transient and multi-species flows in the context of DSMC research with the aim of enhancing the flexibility, extensibility and accuracy of the results [24]. The OpenFOAM version used in this work is OF-v1706 with the addition of the ThirdParty folder and the hyStrath repository [4].

2.1 Computational domain and mesh

The OpenFOAM computational domain is a three dimensional Cartesian coordinate system. The mesh is generated within dsmcFoam+ through the blockMesh and snappyHexMesh applications to generate a rectangular parallelepiped subdivided into hexagonal faces with a determined grid refinement and grading. Its function is to initialise the particles, provide a cell-list algorithm for performing particle collisions, decompose the domain for parallel computations and to resolve macroscopic field properties [24]. When creating a mesh in DSMC, the following criteria must be satisfied:

• The cell size $\varDelta x$ must be smaller or equal to the molecular free path to ensure that the collisions number per cell does not approach the continuum limit [21].

• The cell size $\varDelta x$ must be smaller or equal to the distance travelled by each DSMC particle during one time-step $\varDelta t$ to avoid artificial viscosity [23].

• The equivalent number of particles generated within the domain that represent one real particle $n_{eq}$ should be between 7 and 20 times the number of cells generated within the mesh. When $n_{eq}<7 \cdot n_{cells}$ an inflated number of collision occurs and the accuracy is compromised. Conversely, as $n_{eq}>20 \cdot n_{cells}$ the computational time is unnecessarily increased as this is proportional to $n_{eq}^2$ [2].

Fig. 7

DSMC computational domain for the ABIE air intake

For simplicity reasons, the Graphical User Interface (GUI) simFlow 4.0 [22] is run to generate more advanced meshes; the CAD models in Fig. 6 are first imported as STL files. The surfaces are then separated by means of the split function such that the outlet and walls of each air intake can be classified into their corresponding face groups. The Hex Meshing functionality allows to generate a box-shaped domain that encompasses the imported geometry, as shown in Fig. 7.

According to the aforementioned mesh criteria, the cell size would need to be:

• $\varDelta x \le 105 m$, as $\lambda =\frac{1}{\sqrt{2} \pi \cdot d^2 \cdot n}$ [20] (see Table 3)

• $\varDelta x \le 0.422 m$ as the distance travelled by an individual particle corresponds to $\varDelta t \cdot \sqrt{2R \cdot T/ \overline{M_w}}$ [23], where $\varDelta t =5 \cdot 10^{-4} s$, the molar gas constant is equal to $R=8.3145$ $J/K \cdot mol$ and the other properties are defined in Table 2.

As in every simulation, a trade-off between mesh refinement and computational time exists. In the case of DSMC, this occurs because of the third criterion stated: the number of equivalent particles should be between 7 and 20 times as much as the number of cells. As the cell size is reduced, more cells are generated and, thus, more particles are required. Since the computational time is proportional to $n_{eq}^2$, a longer duration is required. The cell size is therefore chosen to equal $\varDelta x=0.3 m$ by setting the number of divisions to 20 in each Cartesian direction. Moreover, a minimum refinement level of 1 and maximum level of 2 are included in the intake as larger flow gradients are expected within this region; the mesh is shown in Fig. 8.

Fig. 8

Cross sectional view of the ABIE air intake mesh

2.2 Boundary conditions

The dsmcFoam+ solver offers a wide variety of DSMC boundary conditions which are created via the boundariesDict application. These are categorised into dsmcPatchBoundaries, dsmcCyclicBoundaries and dsmcGeneralBoundaries [24]. A total of 6 boundaries are required for the simulation of the ABIE intake; four patches are needed to define the domain whereas one patch and one wall are required to simulate the air intake itself, as shown in Fig. 9.

Fig. 9

DSMC boundary conditions for the ABIE air intake

Regarding the dsmcPatchBoundaries, all the sides, inlet and outlet of the computational domain are set as dsmcDeletionPatch such that the molecules are removed from the domain upon collisions. Furthermore, the intake walls are set as dsmcDiffuseWallPatch, to simulate the diffuse nature of the gas-wall interactions in VLEO [7]. While the velocity on the wall surface is zero, according to the no-slip condition, the wall temperature is calculated to equal 294 K by Fujita [7] by assuming an emissivity coefficient of 0.5 and a flat surface perpendicular to the heat source. A similar approach is undertaken for the air intake outlet, which is programmed as a dsmcAbsorbingDiffuseWallPatch. This is to simulate the outlet as a wall with the same properties just mentioned, in addition to the absorbing functionality of the patch that replicates the transparency of the acceleration grid $\eta _t$. Therefore, the absorption probability of each species is varied throughout the simulations.

On the other hand, the inlet of the domain is set as dsmcFreeStreamInflowPatch under the dsmcGeneralBoundaries. This boundary condition generates a free stream flow of particles with the number density and velocity in in Table 2.

2.3 Molecular model

In the Free Molecular Flow regime, mentioned in Sect. 1.2, the intermolecular collisions may be neglected as the flow is dominated by gas-surface interactions [2]. However, to verify the approach taken in regarding the flow as FMF in the simulation of an ABEP intake, a realistic but sufficiently simple molecular model is required to determine the post-collision velocities of the two colliding particles. While this is easily switched off to noBinaryCollisions in the dsmcProperties file, a molecular model is adopted to compare the simulation results with and without the model. In fact, if the flow is in FMF, the molecular model should not affect the results as only very few inter-molecular collisions are expected. The Variable Hard Sphere (VHS) model is chosen by Fujita [6, 7] to simulate ABIE, and it is therefore chosen as the reference scheme with the properties shown in Table 3. This includes the particle diameter of each species d, its corresponding mass m, internal degrees of freedom (IDOF) and viscosity power $\omega$ [21]. Note that VHS model is enabled throughout the simulations, unless clearly stated otherwise.

Table 3 Parameters for the VHS molecular model [21]

2.4 Time control

Each simulation is run with a time-step $\varDelta t =5 \cdot 10^{-4} s$ and a writing time of $\varDelta t =1 \cdot 10^{-3} s$. The number of DSMC particles inside the domain and their average linear kinetic energy are recorded at each time-step such that their normalised behaviour is plotted over time as in Fig. 10. The convergence criterion requires such parameters to stabilise in order for the results to be meaningful [2]; a convergence time of 0.42s is achieved in order for the percentage change of the normalised values to equal $1\cdot 10^{-6}~\%$ and satisfy the criterion. Within the dsmcFoam+ environment, the startSampling utility is therefore run such that the dsmcVolFields in the fieldPropertiesDict averages the macroscopic field properties across the remaining simulation duration of approximately 8 times as long as the convergence time. This allows for enough data to be averaged over time to counteract the stochastic nature of the simulation [2].

Fig. 10

Convergence criterion for dsmcFoam+ simulations

3 Results and discussion

To visualise the flow behaviour within the air intake, the application ParaView 5.8.0 is used, in which the DSMC computational domain may be imported under the file-format .foam. This allows to compute the compression ratio $\beta$ by displaying the rhoN property for the entire gas mixture and applying Eq. 2. The intake collection efficiency, on the other hand, requires further calculations; the particle flow rate at the outlet $N_{thr}$ is obtained by computing the dot product of the velocity vector with the number density of the gas and, consequently, by integrating the values over the surface area of the outlet itself. This can be executed in the ParaView environment by means of the Integrate Variables utility. Conversely, the inlet flow rate $N_{in}$ is computed analytically from the inflow free stream conditions in Eq. 5 [15], where $S_n$ is the normal component of the speed ratio defined as $\frac{v}{\sqrt{2R \cdot T/ \overline{M_w}}}$. Given the properties in Table 2, $S \approx 9.2$.

$$\begin{aligned} \begin{aligned} N_{in}=\frac{A_{inlet} \cdot \varDelta t \cdot n \cdot \sqrt{2R \cdot T/ \overline{M_w}}}{2 \cdot n_{eq}\cdot \sqrt{\pi }}\times \\ \times \{ e^{-S_n^2} + \sqrt{\pi } \cdot S_n [1+erf(S_n) ]\} \end{aligned} \end{aligned}$$

(5)

3.1 Effect of acceleration grid transparency

As stated in the JAXA papers [6, 7], the acceleration grid located at the intake outlet surface is a component specific to the ABEP concept investigated that is defined as the fraction of particles reaching the thruster to those reaching the base plate in Fig. 5. While this corresponds to a value of $\eta _{t} \approx 0.2$ in the specific case of the Air-Breathing Ion Engine, a study of $\eta _{t}=0,0.1,0.2,0.3,0.4$ is carried out for the air intake with $X=10$. To simulate the variation in $\eta _t$, the Intake-Outlet patch in Fig. 9, with boundary condition dsmcAbsorbingDiffuseWallPatch, allows the modification of the gas absorption probability.

The resulting compression ratio $\beta$ and intake collection efficiency $\eta _c$ are plotted in Fig. 11 against the DSMC data obtained by Fujita [7] and summarised in Table 4 as a function of grid transparency $\eta _t$.

Fig. 11

Performance variation of ABIE with grid transparency $\eta _t$

Table 4 Influence of grid transparency $\eta _t$ on collection efficiency $\eta _c$ and compression ratio $\beta$ against RARAC-3D [7]

The dashed lines plotted in Fig. 11 are shown in Eq. 6 and represent the values simulated in RARAC-3D, with initial compression ratio $\beta _0=177$ [7].

$$\begin{aligned} {\begin{matrix} \beta =\beta _0[1-0.772(1- e^{-8.15 \cdot \eta _t})] \\ \eta _c=0.475(1- e^{-8.15 \cdot \eta _t}) \end{matrix}} \end{aligned}$$

(6)

It is observed that the intake collection efficiency increases with grid transparency, with an exponential rise for $\eta _t \le 10\%$ of $\varDelta \eta _c=25.49\%$ within an increase of $10\%$ in $\eta _t$. In fact, as $\eta _t \rightarrow 40\%$, the gradient of the red line becomes more shallow, only increasing by $4.14\%$ for the same percentage increase in $\eta _t$. This shows that the air intake approaches a theoretical limit for $\eta _c$. Conversely, the compression ratio shows an exponential decrease for $\eta _t \le 10\%$ which becomes less pronounced as $\eta _t \rightarrow 40\%$. This is quantified by the percentage change in $\beta$ for the first $10\%$ increase in $\eta _t$ which is almost twice as much as the variation between $30\% \le \eta _t \le 40\%$. The trends of the two performance parameters is almost symmetrical but opposite about the y-axis; on one hand, allowing more particles to pass through the grid leads to a greater collection efficiency. On the other hand, the compression of the collected particles is reduced as more particles exit the intake. This is exemplary of the intrinsic trade-off between $\beta$ and $\eta _c$, which should be carefully selected according to the mission requirements and constraints.

When comparing the accuracy of dsmcFoam+ with that achieved by RARAC-3D [7], the percentage difference error $\delta _{diff}$ is employed to quantify the discrepancy between the two solvers. From the values in Table 4 it is noticed that a mean percentage error of $\overline{\delta }_{diff}\approx 2.97\%$ for the compression ratio and $\overline{\delta }_{diff}\approx 2.06\%$ for the intake collection efficiency are yielded. The relatively low figures underline the great consistency between dsmcFoam+ and RARAC-3D, with a slightly better agreement on $\eta _c$ than $\beta$. Moreover, it is observed that the maximum $\delta _{diff}$ for both performance parameters is achieved at $\eta _t=40\%$. This is explained by the simulations carried out by Fujita [6, 7], which were performed for a maximum value of $\eta _t=30\%$. Although Eq. 6 has been extrapolated to a greater range, it was recommended to maintain $0\% \le \eta _t \le 30\%$. The results obtained by this paper, however, prove the validity of Eq. 6 even beyond the original range with a reasonable percentage error up until $\eta _t \rightarrow 40\%$.

3.2 Effect of intermolecular collisions

To verify the validity of the FMF flow regime - which assumes the presence of no intermolecular collisions - the VHS molecular model in Sect. 2.3 is turned off and replaced by the NoBinaryCollisions command within the dsmcProperties folder. The ABIE air intake is therefore simulated in dsmcFoam+ with $X=10$, $\eta _t=10\%$ and no binary collisions. It is observed that the collection efficiency reaches a value of $\eta _c=25.90\%$, with an error of only $\delta _{diff}=1.61\%$ when compared to the case in Table 4. The compression ratio $\beta$, on the other hand, yields a slightly larger error of $\delta _{diff}=3.49 \%$ as $\beta \approx 106$. As summarised in Table 5, the percentage errors of both parameters are relatively marginal and prove that the FMF assumption of no binary collisions is valid and may be used to simplify the analysis further.

Although the discrepancy is small, the results show that the presence of intermolecular collisions leads to a slight reduction in the performance of the system. This suggests that the incoming flow molecules collide with those already trapped at the back of the intake and increase the backflow through the lateral ducts [17].

Table 5 Influence of DSMC intermolecular collisions

3.3 Effect of incidence angle

The previous results are pressented under the assumption that the flow is aligned with the direction of flight of the ABIE air intake. However, through the standard operations of a space mission, the S/C might be expected to undergo both orbital and attitude control manoeuvres. Moreover, the presence of external environmental influences, horizontal winds and orbital disturbances may induce torques that would alter the configuration and performance design-point of the ABEP system. More specifically, both manoeuvres and disturbance torques are effects that would cause a variation in the incidence angle of the flow $\alpha$ with respect to the intake. The presence of the angle between the intake and the flow depicted in Fig. 12, and its effect on the compression ratio is therefore investigated.

Fig. 12

Schematic of Velocity Vector with Incidence Angle

The dsmcFreeStreamInflowPatch in Sect. 2.2 is implemented with a variation in the velocity component according to Fig. 12. The individual velocity components along the x and y axes are therefore calculated as $V_x=V \times \cos (\alpha )$ and $V_y=V \times \sin (\alpha )$ for $\alpha =0^{\circ },5^{\circ },10^{\circ },15^{\circ }$ in the ABIE intake with aspect ratio $X=10$. Thus, the characteristic feature of this attitude configuration is that the flow entering the intake has a vertical velocity. The results are plotted qualitatively in Fig. 13 and quantitatively in Fig. 14 against the data obtained by Fujita [6, 7] for $\eta _t=0$.

Fig. 13

ABIE number density distribution for RARAC-3D [6, 7] (left) and dsmcFoam+ (right), with varying incidence angle $\alpha =5^{\circ }$ (top) and $\alpha =15^{\circ }$(bottom), for $X=10$ and $\eta _t=0$

The general distribution trends in Fig. 13 (right) show a rapid decrease in density with incidence angle from $\alpha =5^{\circ }$ to $\alpha =15^{\circ }$, in agreement with RARAC-3D [7] in Fig. 13 (left). This occurs because the collimated flow is not aligned with the system and cannot easily cross the intake itself. Fewer particles are transmitted through ABIE, considering that even the fast particles that would not have collided with the lateral ducts are more likely to be scattered by the intake.

Because of the boundary conditions, the particles scatter diffusely with the walls and reflect randomly inside the intake, hence decreasing the probability of the collected particles to reach the thruster; the overall performance of ABIE is thus reduced. As the main duct can be approximated by a two-dimensional rectangle with aspect ratio 10, the angle between the diagonal and the long side can be computed as $\arctan (X^{-1})$ which equals $5.70^{\circ }$ for the configuration with $X=10$ [7]. When the incidence angle reaches this critical value (i.e. $\alpha =5.70^{\circ }$), the inclined surface at the back of the intake becomes a reflector. A greater number of particles is therefore observed to scatter with the walls of the duct and bounce back outside through the duct. As the variation of compression ratio with incidence angle is plotted in Fig. 14, the presence of a critical angle becomes evident. The performance of the intake appears to suddenly drop at the threshold after which the inclined surface at the back of the intake acts as a reflector. The individual data points of compression ratio for the simulations performed in dsmcFoam+ are also plotted against the RARAC-3D results in Fig. 14, validating the accuracy of both as the discrepancy yielded is $\delta _{diff} \le 1.8 \%$. Although the performance of ABEP intakes is dependant on the geometrical configuration, similar trends as the one observed in Fig. 14 can be retrieved from the literature. For instance, a degradation of $10\%$ in compression ratio is yielded for an angle of $5^{\circ }$ by [15], which increases up to $20-30\%$ for $\alpha =10^{\circ }$, thereby verifying the tendencies obtained.

Fig. 14

Variation of compression ratio $\beta$ with incidence angle $\alpha$ for dsmcFoam+ against RARAC-3D [7]

3.4 Effect of intake aspect ratio

The variation of aspect ratio, quantified by the nondimensional parameter X in Eq. 4, is also investigated. The CAD models in Fig. 6 are all imported in dsmcFoam+ by following the methodology discussed in Sect. 2, with $X=10,20,40$. Note also that the grid transparency is kept as $\eta _t=0$, such that the results can be compared directly with those obtained in RARAC-3D by Fujita [7].

Fig. 15

ABIE number density distribution for RARAC-3D [6, 7] (left) and dsmcFoam+ (right), with varying aspect ratio $X=40$ (top) and $X=10$ (bottom), for $\eta _t=0$

As the nondimensional variable X is increased, the geometry of the air intake results more elongated along the system horizontal axis. Nevertheless, the outer diameter and, consequently, the available inlet area are reduced. As shown in the comparison of number density distribution between $X=10$ and $X=40$ in Fig. 15, it is clear that the overall compression ratio increases with aspect ratio. This is in accordance with the DSMC simulations performed on the RARAC-3D solver by Fujita [6, 7], shown on the left-hand side of Fig. 15.

For a more quantitative comparison, Eq. 7 has been extrapolated by Fujita [7] and plotted in Fig. 16 as a benchmark for the dsmcFoam+ results shown in Table 6.

$$\begin{aligned} \beta =\beta _0(0.244-0.330 \ln (X^{-1})) \end{aligned}$$

(7)

Table 6 Influence of aspect ratio X on the compression ratio $\beta$ against RARAC-3D [7] for $\eta _t=0$

Fig. 16

Variation of compression ratio $\beta$ with aspect ratio X for dsmcFoam+ against RARAC-3D [7]

It is observed that the dsmcFoam+ values are in strong agreement with those obtained via RARAC-3D [6], as the mean absolute percentage error for the three individual data points collected is $1.10\%$. While a narrower inlet area and more elongated geometry might result beneficial for the compression ratio of the propulsion system, it is also important to consider the increase in weight that such an variation in aspect ratio would cause at a system-level [7].

3.5 Atmospheric drag coefficient and power requirements

The atmospheric drag force is the result of an exchange of momentum caused by the impact of the flow particles against the S/C surfaces. The purpose of the on board propulsion system, or ABEP in the case of this particular study, is to generate a force in the opposite direction of the drag vector to compensate - either partially or fully - the decaying effect of the colliding particles. An accurate estimation of the amount of drag experienced by a S/C in service is therefore crucial.

A preliminary approach to quantify the atmospheric drag D is to adopt Eq. 8, where A refers to the cross sectional area perpendicular to the direction of flight and $C_d$ is the drag coefficient [16].

$$\begin{aligned} D=\frac{1}{2} \cdot \rho \cdot V^2 \cdot A \cdot C_d \end{aligned}$$

(8)

All the parameters on the right-hand side of Eq. 8 are already defined in Tables 1 and 2, except from the drag coefficient which is of particular interest for this research. While a standard theoretical figure of $C_d=2$ has been chosen by Fujita for the cross sectional area of the satellite [6, 7], a DSMC investigation is hereby undertaken for the ABIE intake. While this simplification does not include the solar array panels and aerodynamic surfaces shown in Fig. 3, it is considered representative for the aerodynamic conditions experienced by the cross sectional area of the satellite that faces towards the direction of flight as described in the original design of the engine  [12]. Thus, it is noted that this approximation is only valid for a horizontal flight with no incidence angle with the flow.

The forceCoeffs function object is coded at the end of the controlDict script to measure the force coefficients along the main body axes by specifying the free stream parameters in Table 2. In addition, the reference length of the flow is calibrated as $R_2$ in Fig. 5, and the cross sectional area of the S/C is set as $\pi \cdot R_2^2$. As the drag coefficient - corresponding to the body force coefficient along the x-axis - is obtained, the drag force is computed by means of Eq. 8.

The three configurations of the ABIE air intake with intake aspect ratio $X=10,20,40$ are simulated in dsmcFoam+ and the drag results are reported in Table 7. It is observed that as X is increased, the cross sectional area of the S/C perpendicular to the flow decreases. This causes an increase in $C_d$ and consecutive reduction of atmospheric drag. While this might appear to benefit the overall system, it is essential to satisfy the condition for full drag compensation: the amount of thrust produced must equal the atmospheric drag experienced by the S/C. This is represented by Eq. 9, where the thrust is calculated as the product of the gas mass flow rate $\dot{m}$ and its exhaust velocity $v_{ex}$ [6].

$$\begin{aligned} \frac{1}{2} \cdot \rho \cdot V^2 \cdot A \cdot C_d=\dot{m} \cdot v_{ex} \end{aligned}$$

(9)

Table 7 Atmospheric drag dsmcFoam+ results

The mass flow rate can then be calculated according to Eq. 10, where $\zeta$ is the ratio of the air intake cross sectional area to the satellite cross sectional area such that $\zeta =1-(1+L_1/X \cdot R_1)^{-2}$, and the ion-engine propellant utilization efficiency is $\eta _u=0.8$ [6].

$$\begin{aligned} \dot{m}= \rho \cdot v \cdot A \cdot \zeta \cdot \eta _c \cdot \eta _u \end{aligned}$$

(10)

The exhaust velocity required by the propulsion system is hence computed in Eq. 11, by substituting Eq. 10 into Eq. 9.

$$\begin{aligned} v_{ex}=\frac{v \cdot C_d}{2 \cdot \eta _c \cdot \eta _u} \end{aligned}$$

(11)

Lastly, to establish the feasibility of such a propulsion system, the ion-engine acceleration power $P_a$ is calculated from Eq. 12, under the assumption that the ion acceleration is performed ideally. This is an essential parameter to consider at a system-level as it defines the amount of power required by the power subsystem. In a self-sustained system, in fact, the choice of ABEP is usually complemented with the use of solar arrays and on board batteries.

$$\begin{aligned} P_a=\dot{m} \cdot v_{ex}^2/2 \end{aligned}$$

(12)

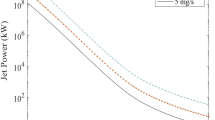
It is important to note that the thrust generated by ABEP intakes, and therefore the ion-engine power acceleration, is a function of the intake collection efficiency. A plot of power density requirements $p_a$ is shown in Fig. 17 for the range of intake collection efficiency $0\% \le \eta _c \le 50\%$.

Fig. 17

Power density requirements for varying air intake collection efficiency and aspect ratio $X=10,20,40$

As the intake is elongated, the power density requirements increase remarkably due to the large decrease in mass flow rate within the intake for a small reduction of frontal drag area. For the same intake collection efficiency of $\eta _c=40\%$, $2.23~kW/m^2$ are required for $X=10$, $3.96~kW/m^2$ for $X=20$ and $26.21~kW/m^2$ for $X=40$. A lower aspect ratio would therefore be preferred to reduce the power requirements, although this would lead to a reduction in the compression ratio as shown in Table 6. In the context of ion-engine acceleration power, the acceleration voltage is of significant importance for the exhaust velocity as the latter is proportional to the square of the former, as shown in Eq. 13. Similarly, the ion-engine beam current density can be formulated in Eq. 14, where e is the elementary charge of an electron in coulombs, from which the relationship with the required power density is clear.

$$\begin{aligned} V_{\mathrm {A}}=\frac{m \cdot v_{\mathrm {ex}}^{2} }{2 e} \end{aligned}$$

(13)

$$\begin{aligned} i=\frac{\dot{m} \cdot e }{m \cdot A} \end{aligned}$$

(14)

The results for the beam voltage and current density corresponding to the power requirements in Fig. 17 are shown in Table 8 from which it is observed that the acceleration voltage decreases with increasing of intake collection efficiency, while the acceleration current density increases. For any required conditions to be satisfied in terms of beam current and voltage, Table 8 can be used to determine the permissible range under which the intake can operate.

Table 8 Beam acceleration voltage, acceleration current density and power density

Hence, the power subsystem should be carefully sized and traded-off with the performance of the propulsion system. However, high levels of power density could result unpractical; the intake collection efficiency $\eta _c$ and propellant utilization efficiency $\eta _u$ should ideally be optimised. The results shown in Table 4, for instance, show that the former could be improved by increasing the transparency of the acceleration grids.

4 Conclusion

This paper focused on the validation of the ABIE air intake performance by proposing an alternative and accessible simulation methodology for the numerical analysis of the engine through the dsmcFoam+ open source solver. Following the introduction to the VLEO environment along with its major benefits, a review of the ABIE operation principle and available studies is carried out in which the key design components were outlined. To evaluate the performance of the intake, its collection efficiency and compression ratio have been defined as design drivers of the system component.

As the modelling process is strictly bound to the the geometrical configuration of the intake along with the free stream atmospheric conditions, the intake dimensions as well as the environmental conditions at an altitude of 180 km have been implemented as obtained by Fujita [7] through the MSISE-90 atmospheric model. The air intake CAD models with varying aspect ratios were then imported and meshed within the dsmcFoam+ computational domain, where the DSMC criteria for grid size and number of particles have been satisfied. Similarly, the boundary conditions have been assigned according to the free stream conditions identified and the VHS binary collision model implemented.

Finally, the results obtained were discussed in the context of the system performance and compared with the DSMC simulations performed in RARAC-3D [6, 7] as hereby summarised:

• 1. The transparency of the acceleration grids has been varied between $0 \% \le \eta _t \le 40 \%$ for $X=10$, showing that while the intake collection efficiency is improved as $\eta _t$ increases, the compression ratio decreases in a specular fashion. When comparing the dsmcFoam+ results to RARAC-3D, the percentage difference is calculated. Although the error increases with the magnitude of $\eta _t$, a reasonable value of $\overline{\delta }_{diff}=2.97 \%$ is yielded for the compression ratio and $\overline{\delta }_{diff}=2.06 \%$ for the collection efficiency. While dsmcFoam+ seems to predict the latter parameter more accurately, the discrepancy of both figures is relatively small.

• 2. When the VHS molecular model was deactivated for the configuration with $X=10$ and $\eta _t=10 \%$, the intake performance was improved as the collection efficiency increased by $1.61 \%$ and the compression ratio by $3.49 \%$. The small increase, attributed to the reduction in backflow, validated the FMF assumption of no binary collisions.

• 3. As the attitude of a S/C varies throughout its operations, the effect of flow misalignment was simulated for the $X=10$ and $\eta _t=0$ configuration with $\alpha =0^{\circ }, 5^{\circ }, 10^{\circ }, 15^{\circ }$. An increase in $\alpha$ beyond the critical angle of $5.7^{\circ }$ resulted in a rapid decrease in chamber density, hence reducing the overall compression ratio. This is because of the greater number of particles scattering with the duct walls and hence bouncing back outside the intake. Even under these circumstances, the discrepancy between dsmcFoam+ and RARAC-3D was relatively small as $\delta _{diff} \le 1.8\%$.

• 4. By increasing the intake aspect ratio from $X=10$ to $X=20$ and, consequently, to $X=40$, the compression ratio significantly increased by $21 \%$ and $18 \%$ respectively. This occurred as more particles were trapped inside the intake by the narrower lateral passage. This was in accordance with the RARAC-3D results as the percentage difference yielded was $\delta _{diff} \le 1.83\%$.

• 5. As opposed to the theoretical value of $C_d=2$, the coefficient of drag of the air intake with configurations $X=10,20,40$ was simulated in dsmcFoam+, yielding an increase in $C_d$ as X was increased. The more accurate values of $C_d$ were thus employed to compute the exhaust velocity, mass flow rate and, therefore, the beam acceleration voltage, acceleration current density and power density required for full drag compensation. The relevance of establishing such requirements lies in constraining the operational envelope of the system, depending on the intake configuration, collection efficiency and power available.

To conclude, the DSMC results of the ABIE air intake retrieved from the literature have been validated by means of the dsmcFoam+ code within the OpenFOAM toolbox, as a strong and consistent agreement was observed with the RARAC-3D data. Whilst this paper simulated the ABIE air intake, the methodology devised within dsmcFoam+ may be applied to the design and optimisation process of any passive ABEP intake as its accuracy has been verified. With suitable assumptions, the computational cost of the simulations can be reduced even further but the accuracy could be compromised. The DSMC technique implemented therefore represents an analysis method of high modelling capabilities. In addition to the validation of the ABIE performance, the DSMC methodology proposed within a publicly available solver supports the development of ABEP technologies on a much broader scale.

4.1 Future work

Given the profound dependency between the free stream conditions and the intake performance, the atmospheric conditions of interest should be evaluated more precisely; the MSISE-90 is a representative atmospheric model and its data should only be used for preliminary results. To increase the accuracy of future simulations, further empirical data should be collected within the specific geographical and temporal envelope of interest for the mission. To optimise the performance of the ABIE intake, the addition of a honeycomb duct at the inlet could be implemented, as this has been shown to act as a molecular trap, thereby reducing the backflow of the incoming flow [17, 18]. Furthermore, given the importance of the gas-surface interaction model chosen, materials that lead to specular collisions should be investigated and adopted as DSMC simulations of specular intakes yielded intake collection efficiencies of up to 94% [18]. Moreover, an experimental verification should be conducted to validate the DSMC results presented in this paper. For instance, the Rarefied Orbital Aerodynamics Research (ROAR) facility is currently being used to test ABEP intake models on the ground [13]. Additionally, in-flight data would be extremely valuable towards the accurate measurement of in-situ flow behaviour.