Skip to main content
SpringerLink
Log in

Tensor Product Based Polytopic LPV System Design of a 6-DoF Multi-strut Platform

  • Regular Papers
  • Control Theory and Applications
  • Published:
International Journal of Control, Automation and Systems Aims and scope Submit manuscript

Abstract

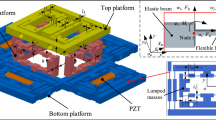
Multi-strut platform is widely used for precise instrument vibration isolation. In this paper, a Newton-Euler based 6-DOF 12-strut platform model is proposed. Nonlinearity of platform dynamic component is derived by establishing polytopic linear parameter varying (LPV) system. To guarantee the linearization accuracy of LPV system while reducing model elements to a real-time computing level. Tensor product(TP) model transformation and truncated high-order singular value decomposition(HOSVD) are used to decompose LPV system high-order tensor into unique principle basis. Then low-rank approximation of system is implemented by discarding minor singular basis vectors, for the sake of minimizing storage space and computing complexity. And then the parameter varying system is represented by convex combination of discretized system vertexes. So quadratic regulator method can be applied to vertex linear time-invariant subsystem controller to construct the global controller. Performance of the proposed multi-strut platform is demonstrated through hardware in loop simulation.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. D. DiFrancesco, A. Grierson, K. Dan, and T. Meyer, “Gravity gradiometer systems — Advances and challenges,” Geophysical Prospecting, vol. 57, no. 4, pp. 615–623, 2009.

    Article  Google Scholar 

  2. C. Jekeli, “A review of gravity gradiometer survey system data analyses,” Geophysics, vol. 58, no. 4, pp. 508–514, 1993.

    Article  Google Scholar 

  3. D. Stewart, “A platform with six degrees of freedom,” Archive Proceedings of the Institution of Mechanical Engineers, 1847–1982 (vols. 1–196), no. 180, pp. 371–386, 1965.

    Google Scholar 

  4. E. F. Fichter, “A stewart platform-based manipulator: General theory and practical constrution,” The International Journal of Robotics Research, vol. 5, no. 2, pp. 157–182, 1986.

    Article  Google Scholar 

  5. W. Q. D. Do and D. C. H. Yang, “Inverse dynamic analysis and simulation of a platform type of robot,” Journal of Robotic Systems, vol. 5, no. 3, pp. 209–227, 1988.

    Article  Google Scholar 

  6. B. Dasgupta and T. S. Mruthyunjaya, “A Newton-Euler formulation for the inverse dynamics of the Stewart platform manipulator,” Mechanism and Machine Theory, vol. 33, no. 8, pp. 1135–1152, 1998.

    Article  MathSciNet  Google Scholar 

  7. B. Dasgupta and T. S. Mruthyunjaya, “Closed-form dynamic equations of the general Stewart platform through the Newton—Euler approach,” Mechanism and Machine Theory, vol. 33, no. 7, pp. 993–1012, 1998.

    Article  MathSciNet  Google Scholar 

  8. Y. Nakamura, H. Kawakami, and S. Wakui, “Bandwidth expansion of a pressure control system for pneumatic antivibration apparatuses in presence of dead time,” Journal of Advanced Mechanical Design Systems & Manufacturing, vol. 9, no. 3, pp. 495–500, 2015.

    Article  Google Scholar 

  9. M. D. Emami, S. A. Mostafavi, and P. Asadollahzadeh, “Modeling and simulation of active hydro-pneumatic suspension system through bond graph,” Mechanika, vol. 17, no. 3, pp. 312–317, 2011.

    Article  Google Scholar 

  10. H. Du and N. Zhang, “Fuzzy control for nonlinear uncertain electrohydraulic active suspensions with input constraint,” IEEE Transactions on Fuzzy Systems, vol. 17, no. 2, pp. 343–356, 2009.

    Article  Google Scholar 

  11. Y. Zhang, A. G. Alleyne, and D. Zheng, “A hybrid control strategy for active vibration isolation with electrohydraulic actuators,” Control Engineering Practice, vol. 13, no. 3, pp. 279–289, 2005.

    Article  Google Scholar 

  12. N. R. Fisco and H. Adeli, “Smart structures: Part I — Active and semi-active control,” Scientia Iranica, vol. 18, no. 3A, pp. 275–284, 2011.

    Article  Google Scholar 

  13. E. Guglielmino, G. Gheorghe, M. Giuclea, T. Sireteanu, and C. W. Stammersl, Semi-active Suspension Control: Improved Vehicle Ride and Road Friendliness, 2008.

    MATH  Google Scholar 

  14. Q. Rong and G. W. Irwin, “LMI-based control design for discrete polytopic LPV systems,” Proc. of European COntrol Conference (ECC), IEEE, pp. 1489, 2003.

    Google Scholar 

  15. W. Xie, Y. Kamiya, and T. Eisaka, “Robust model matching for polytopic LPV plant,” IEEJ Transactions on Electronics, Information and Systems, vol. 123, no. 11, pp. 1989–1995, 2004.

    Article  Google Scholar 

  16. P. Apkarian, P. Apkarian, and P. Gahinet, “A convex characterization of gain-scheduled H∞ controllers,” IEEE Transactions on Automatic Control, vol. 40, no. 5, pp. 853–864, 1995.

    Article  MathSciNet  Google Scholar 

  17. P. Baranyi, “Convex hull generation methods for polytopic representations of LPV models,” Proc. of 7th International Symposium on Applied Machine Intelligence and Informatics, pp. 69, 2009.

    Google Scholar 

  18. P. Zoltan, “Polytopic decomposition of linear parametervarying models by tensor-product model transformation,” Applied Mechanics and Materials, vol. 203, pp. 142–147, 2006.

    Google Scholar 

  19. L. Lathauwer, B. de Moor, and J. Vandewalle, “A multilinear singular value decomposition,” SIAM Journal on Matrix Analysis and Applications, vol. 21, no. 4, pp. 1253–1278, 2000.

    Article  MathSciNet  Google Scholar 

  20. L. Szeidll, P. Baranyi, Z. Petres, and P. Varlaki, “Numerical reconstruction of the HOSVD based canonical form of polytopic dynamic models,” Proc. of International Symposium on Computational Intelligence and Intelligent Informatics, Morocco, 2007.

    Google Scholar 

  21. P. Baranyi, “Tensor-product model-based control of twodimensional aeroelastic system,” Journal of Guidance, Control, and Dynamics, vol. 29, no. 2, pp. 391–400, 2006.

    Article  Google Scholar 

  22. B. Takarics and P. Baranyi, “Tensor-product-model-based control of a three degrees-of-freedom aeroelastic model,” Journal of Guidance, Control, and Dynamics, vol. 36, no. 5, pp. 1527–1533, 2013.

    Article  Google Scholar 

  23. L. Wu, J. Li, F. Ma, and L. Yang, “Optimal antivibration design of vehicle-mounted vibration isolation platform,” SAE Technical Papers, 2018-01-1400, 2018. DOI: https://doi.org/10.4271/2018-01-1400

    Google Scholar 

  24. L. Liu, G. Zheng, and W. Huang, “Multi-strut platform for passive whole-spacecraft vibration isolation,” Chinese Journal of Applied Mechanics, vol. 22, no. 3, pp. 329–334, 2005.

    Google Scholar 

  25. P. Baranyi, TP-Model Transformation-Based-Control Design Frameworks, 2016.

    Book  Google Scholar 

  26. P. Baranyi, Y. Yam, and P. Várlaki, “Tensor product model transformation in polytopic model-based control,” Reference & Research Book News, vol. 28, no. 6, 2013.

    Google Scholar 

  27. T. G. Kolda and B. W. Bader, “Tensor decompositions and applications,” SIAM Review, vol. 51, no. 3, pp. 455–500, 2009.

    Article  MathSciNet  Google Scholar 

  28. R. E. Bellman, Matrix Analysis, McGraw-Hill, NY, 1978.

    MATH  Google Scholar 

  29. P. A. Regalia and S. K. Mitra, “Kronecker products, unitary matrices and signal processing applications,” SIAM Review, vol. 31, no. 4, pp. 586–613, 1989.

    Article  MathSciNet  Google Scholar 

  30. J. V. Manjón, P. Coupé, L. Concha, A. Buades, D. L. Collins, and M. Robles, “Diffusion weighted image denoising using overcomplete local PCA,” PloS One, vol. 8, no. 9, pp. e73021–e73021, 2013.

    Article  Google Scholar 

  31. N. Hao, M. E. Kilmer, K. Braman, and R. C. Hoover, “Facial recognition using tensor-tensor decompositions,” SIAM Journal on Imaging Sciences, vol. 6, no. 1, pp. 437–463, 2013.

    Article  MathSciNet  Google Scholar 

  32. K. Batselier, C. Ko, and N. Wong, “Tensor network subspace identification of polynomial state space models,” Automatica, vol. 95, pp. 187–196, 2018.

    Article  MathSciNet  Google Scholar 

  33. B. Gunes, J. van Wingerden, and M. Verhaegen, “Tensor networks for MIMO LPV system identification,” International Journal of Control, vol. 93, no. 4, pp. 797–811, 2020.

    Article  MathSciNet  Google Scholar 

  34. L. Lü, M. Medo, H. Y. Chi, Y. C. Zhang, Z. K. Zhang, and T. Zhou, “Recommender systems,” Physics Reports, vol. 519, no. 1, pp. 1–49, 2012.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. State Key Laboratory of Automotive Simulation and Control, Jilin University, Changchun, China

    Fangwu Ma & Liang Wu

  2. College of Automotive Engineering, Jilin University, Changchun, China

    Jinhang Li & Daofa Yuan

Authors
  1. Fangwu Ma
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jinhang Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Liang Wu
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Daofa Yuan
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jinhang Li.

Additional information

Publisher’s Note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Fangwu Ma received his B.S. and M.S. degrees in automotive engineering from Jilin University in 1982 and 1988, and his Ph.D. degree from the Imperial College London, in 1999. His research interests include wheel-legged robot, all-terrain vehicle, intelligent vehicle, and lightweight design. He is the SAE Fellow and the VP of FISITA.

Jinhang Li received his B.S. degree in automotive engineering from Jilin University in 2016, and he is now a Ph.D. candidate from Jilin University. His research interests include nonlinear control, adaptive control, and system identification.

Liang Wu received his Ph.D. in engineering for Gyeongsang National University (GNU), Korea in 2015. His research interests include Vehicle Dynamics, attitude motion control and vibration isolating control. He is currently an Associate Professor in The State Key Laboratory of Automotive Simulation and Control, Jilin University, China.

Daofa Yuan received his B.S. degree from Hainan University. He has been working for M.S. degree from Jilin University since September 2019. His research interets include semi-active control and intelligent algorithms.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ma, F., Li, J., Wu, L. et al. Tensor Product Based Polytopic LPV System Design of a 6-DoF Multi-strut Platform. Int. J. Control Autom. Syst. 20, 137–146 (2022). https://doi.org/10.1007/s12555-020-0318-8

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12555-020-0318-8

Keywords

Search

Navigation