Skip to main content
SpringerLink
Log in

Robust Guaranteed Cost Control for a Class of Nonlinear 2-D Systems with Input Saturation

  • Regular Papers
  • Control Theory and Applications
  • Published:
International Journal of Control, Automation and Systems Aims and scope Submit manuscript

Abstract

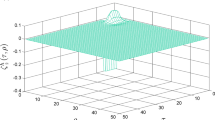
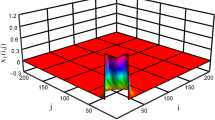
In this paper, a robust guaranteed cost controller is designed for a class of two-dimensional(2-D) discrete-time systems described by Roesser model, where the system simultaneously contains input saturation, parametric uncertainty and sector nonlinearity. Firstly, a convex hull representation is used to describe saturated input of the system. Secondly, a sufficient condition for ensuring the asymptotic stability of the closed-loop system and the existence of the robust guaranteed cost controller is given according to the Lyapunov stability theory. Then, this sufficient condition is transformed into a linear matrix inequality form by using Schur complement lemma and the design of robust guaranteed cost controller is realized by the solution of LMI. Finally, a numerical example is given to illustrate the effectiveness of the proposed method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. R. P. Roesser, “A discrete state-space model for linear image processing,” IEEE Transactions on Automatic Control, vol. 20, no. 1, pp. 1–10, February 1975.

    Article  MathSciNet  Google Scholar 

  2. H. Xu and Y. Zou, “Robust H-infinity filtering for uncertain two-dimensional discrete systems with state-varying delays,” International Journal of Control, Automation, and System, vol. 8, no. 4, pp. 720–726, August 2010.

    Article  Google Scholar 

  3. Y. Ren and D. W. Ding, “Integrated fault detection and control for two-dimensional Roesser systems,” International Journal of Control, Automation, and System, vol. 15, no. 2, pp. 722–731, April 2017.

    Article  Google Scholar 

  4. Q. Y. Xu, X. D. Li, and M. M. Lv, “Adaptive ILC for tracking non-repetitive reference trajectory of 2-D FMM under random boundary condition,” International Journal of Control, Automation, and System, vol. 14, no. 2, pp. 478–485, April 2016.

    Article  Google Scholar 

  5. D. Yang, G. D. Zong, and H. R. Karimi, “H∞ refined anti-disturbance control of switched LPV systems with application to aero-engine,” IEEE Transactions on Industrial Electronics, 2019. DOI: https://doi.org/10.1109/TIE.2019.2912780

    Article  Google Scholar 

  6. K. Wan and X. D. Li, “High-Order Internal Model-Based Iterative Learning Control for 2-D Linear FMMI Systems With Iteration-Varying Trajectory Tracking,” IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2019. DOI: https://doi.org/10.1109/TSMC.2019.2897459

  7. Z. X. Duan and Z. R. Xiang, “Finite frequency H∞ control of 2-D continuous systems in Roesser model,” Multidimensional Systems and Signal Processing, vol. 28, no. 4, pp. 1481–1497, October 2017.

    Article  MathSciNet  Google Scholar 

  8. I. Ghous, Z. R. Xiang, and H. R. Karimi, “H∞ control of 2–D continuous Markovian jump delayed systems with partially unknown transition probabilities,” Information Sciences, vol. 382, pp. 274–291, October 2017.

    Article  Google Scholar 

  9. I. Ghous and Z. R. Xiang, “H∞ control of a class of 2-D continuous switched delayed systems via state-dependent switching,” International Journal of Systems Science, vol. 47, no. 2, pp. 300–313, 2016.

    Article  MathSciNet  Google Scholar 

  10. S. X. Ye and W. Q. Wang, “Stability analysis and stabilisation for a class of 2-D nonlinear discrete systems,” International Journal of Systems Science, vol. 42, no. 5, pp. 839–851, May 2011.

    Article  MathSciNet  Google Scholar 

  11. J. T. Dai, Z. Z. Guo, and S. L. Wang, “Robust H∞ control for a class of 2-D nonlinear discrete stochastic systems,” Circuits, Systems, and Signal Processing, vol. 32, no. 5, pp. 2297–2316, March 2013.

    Article  MathSciNet  Google Scholar 

  12. X. H. Bu, H. Q. Wang, Z. S. Hou, and W. Qian, “Stabilisation of a class of two-dimensional nonlinear systems with intermittent measurements,” IET Control Theory and Applications, vol. 8, no. 15, pp. 1596–1604, October 2014.

    Article  MathSciNet  Google Scholar 

  13. X. H. Bu, J. Q. Liang, Z. S. Hou, and J. Q. Yang, “Quantized H infinity control for a class of 2-D systems with missing measurements,” International Journal of Control, Automation, and System, vol. 15, no. 2, pp. 706–715, April 2017.

    Article  Google Scholar 

  14. P. Kokil, “An improved criterion for the global asymptotic stability of 2-D discrete state-delayed systems with saturation nonlinearities,” Circuits, Systems and Signal Processing, vol. 36, no. 6, pp. 2209–2222, June 2017.

    Article  MathSciNet  Google Scholar 

  15. H. L. Xu, Y. Zou, J. W. Lu, and S. Y. Xu, “Robust H∞ control for a class of uncertain nonlinear two-dimensional systems with state delays,” Journal of the Franklin Institute, vol. 342, no. 7, pp. 877–891, November 2005.

    Article  MathSciNet  Google Scholar 

  16. H. K. Khalil, Nonlinear Systems, Upper Saddle River, 2002.

  17. H. L. Ren, G. D. Zong, and T. S. Li, “Event-triggered finite-time control for networked switched linear systems with asynchronous switching,” IEEE Transactions on Systems, Man, and Cybernetics: Systems, vol. 48, no. 11, pp. 1874–1884, November 2018.

    Article  Google Scholar 

  18. H. L. Ren, G. D. Zong, and K. H. Reza, “Asynchronous finite-time filtering of networked switched systems and its application: an event-driven method,” IEEE Transactions on Circuits and Systems — I: Regular Papers, vol. 66, no. 1, pp. 391–402, January 2019.

    Article  MathSciNet  Google Scholar 

  19. R. H. Wang, L. L. Hou, G. D. Zong, S. M. Fei, and D. Yang, “Stability and stabilization of continuous-time switched systems: A multiple discontinuous convex Lyapunov function approach,” International Journal of Robust and Nonlinear Control, vol. 29, no. 5, pp. 1499–1514, March 2019.

    Article  MathSciNet  Google Scholar 

  20. G. D. Zong, H. L. Ren, and L. L. Hou, “Finite-time stability of interconnected impulsive switched systems,” IET Control Theory and Applications, vol. 10, no. 6, pp. 648–654, March 2016.

    Article  MathSciNet  Google Scholar 

  21. G. D. Zong, R. H. Wang, W. X. Zheng, and L. L. Hou, “Finite-time H∞ control for discrete-time switched nonlinear systems with time delay,” International Journal of Robust and Nonlinear Control, vol. 25, no. 6, pp. 914–936, April 2015.

    Article  MathSciNet  Google Scholar 

  22. H. Fertik and C. Ross, “Direct digital control algorithm with anti-windup feature,” IET Control Theory and Applications, vol. 6, no. 4, pp. 317–328, October 1967.

    Google Scholar 

  23. A. Glattfelder and W. Schaufelberger, “Stability analysis of single-loop control systems with saturation and antireset-windup circuits,” IEEE Transactions on Automatic Control, vol. 28, no. 12, pp. 1074–1081, December 1983.

    Article  Google Scholar 

  24. E. F. Mulder, M. V. Kothare, and M. Morari, “Multivariable anti-windup controller systhesis using linear matrix inequlities,” Automatica, vol. 37, pp. 1407–1416, October 2001.

    Article  Google Scholar 

  25. Y. Y. Cao, Z. L. Lin, and T. Hu, “Stability analysis of linear time-delay systems subject to input saturation,” IEEE Transactions on Circuits and Systems I, vol. 49, no. 2, pp. 233–240, February 2002.

    Article  MathSciNet  Google Scholar 

  26. T. Hu, Z. Lin, and B. M. Chen, “Analysis and design for discrete-time linear systems subject to actuator saturation,” Systems & Control Letters, vol. 45, no. 2, pp. 97–112, February 2002.

    Article  MathSciNet  Google Scholar 

  27. A. Benzaouia, F. Tadeo, and F. Mesquine, “The regulator problem for linear systems with saturations on the control and its increments or rate: An LMI approach,” IEEE Transactions on Circuits and Systems I, vol. 53, no. 12, pp. 2681–2691, December 2006.

    Article  MathSciNet  Google Scholar 

  28. A. Hmamed, F. Mesquine, and F. Tadeo, “Stabilization of 2-D saturated systems by state feedback control,” Multidimensional Systems and Signal Processing, vol. 21, no. 3, pp. 277–292, October 2010.

    Article  MathSciNet  Google Scholar 

  29. S. Huang, Z. Xiang, and H. Karimi, “Robust l2-gain control for 2-D nonlinear stochastic systems with time-varying delays and actuator saturation,” Journal of the Franklin Institute, vol. 350, no. 7, pp. 1865–1885, September 2013.

    Article  MathSciNet  Google Scholar 

  30. B. R. Barmish, “Necessary and sufficient conditions for quadratic stabilizability of an uncertain system,” Journal of Optimization Theory and Applications, vol. 46, no. 4, pp. 399–408, August 1985.

    Article  MathSciNet  Google Scholar 

  31. S. Chang and T. Peng, “Adaptive guaranteed cost control of systems with uncertain parameters,” IEEE Transactions on Automatic Control, vol. 17, no. 4, pp. 474–483, August 1972.

    Article  MathSciNet  Google Scholar 

  32. X. Guan, C. Long, and G. Duan, “Robust optimal guaranteed cost control for 2D discrete systems,” IEE Proc. Control Theory Applications, vol. 148, no. 5, pp. 355–361, September 2001.

    Article  Google Scholar 

  33. A. Dhawan and H. Kar, “An LMI approach to robust optimal guaranteed cost control of 2-D discrete systems described by the Roesser model,” Signal Processing, vol. 90, no. 9, pp. 2648–2654, September 2010.

    Article  Google Scholar 

  34. A. Dhawan and H. Kar, “An improved LMI-based criterion for the design of optimal guaranteed cost controller for 2-D discrete uncertain systems,” Signal Processing, vol. 91, no. 4, pp. 1032–1035, April 2011.

    Article  Google Scholar 

  35. W. Chen and W. Zhang, “A 2D-based approach to guaranteed cost repetitive control for uncertain discrete-time systems,” Optimal Control Applications and Methods, vol. 32, no. 6, pp. 720–733, April 2011.

    Article  MathSciNet  Google Scholar 

  36. A. Tandon and A. Dhawan, “Non-fragile robust optimal guaranteed cost control of uncertain 2-D discrete state-delayed systems,” International Journal of Systems Science, vol. 47, no. 14, pp. 3303–3319, December 2016.

    Article  MathSciNet  Google Scholar 

  37. L. V. Hien and H. Trinh, “Switching design for suboptimal guaranteed cost control of 2-D nonlinear switched systems in the Roesser model,” Nonlinear Analysis: Hybrid Systems, vol. 24, pp. 45–57, May 2017.

    MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Electrical Engineering and Automation, Henan Polytechnic University, Century Avenue 2001, Jiaozuo, 454000, China

    Xuhui Bu, Jiaqi Liang, Sen Wang & Wei Yu

Authors
  1. Xuhui Bu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jiaqi Liang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Sen Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Wei Yu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Xuhui Bu.

Additional information

Publisher’s Note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Recommended by Associate Editor Guangdeng Zong under the direction of Editor Hamid Reza Karimi. This work was supported by the National Natural Science Foundation of China (Nos. 61573129, U1804147), the Innovative Scientists and Technicians Team of Henan Polytechnic University (T2019-2, T2017-1), the Innovative Scientists and Technicians Team of Henan Provincial High Education (20IRTSTHN019), and the Innovation Scientists and Technicians Troop Construction Projects of Henan Province (CXTD2016054).

Xuhui Bu received his Bachelor’s and Master’s degrees in automation control from Henan Polytechnic University, Jiao-Zuo, China, in 2004 and 2007, respectively, and his Ph.D. degree in control thoery and application from Beijing Jiaotong University, Beijing, China, in 2011. He is currently an Associate Professor in Henan Polytechnic University, JiaoZuo, China. He has authored over 50 peer-reviewed journal papers and over 20 papers in prestigious conference proceedings. His research is mainly related to data-driven control, iterative learning control, traffic control and networked system control.

Jiaqi Liang was born in 1992. She is currently a doctor graduate student in mining control engineering, with Henan Polytechnic University, jiaozuo, China. She received her Bachelor’s degree in computer science and technology from Henan University of Science and Technology and Master’s degree in Control Science and Engineering from Henan Polytechnic University, in 2014 and 2018, respectively. Her research is mainly related to iterative learning control, mulit-agent systems control.

Sen Wang was born in 1994. He received his Bachelor’s degree in automation control from Henan Polytechnic University, Jiaozuo, China, in 2016. He is currently pursuing an Master’s degree in Control Science and Engineering with Henan Polytechnic University, Jiaozuo, China. His current research interests include two-dimensional system theory, network control systems.

Wei Yu was born in 1994, and received his B.Sc. from Henan Polytechnic University in 2018. Now he is an M.Sc. candidate in Henan Polytechnic University. The main researchdirection is model-free adaptive control.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Bu, X., Liang, J., Wang, S. et al. Robust Guaranteed Cost Control for a Class of Nonlinear 2-D Systems with Input Saturation. Int. J. Control Autom. Syst. 18, 513–520 (2020). https://doi.org/10.1007/s12555-019-0455-0

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12555-019-0455-0

Keywords

Search

Navigation