Skip to main content
SpringerLink
Log in

A New Global Robust Exponential Stability Criterion for H∞ Control of Uncertain Stochastic Neutral-type Neural Networks with Both Timevarying Delays

  • Regular Paper
  • Control Theory and Applications
  • Published:
International Journal of Control, Automation and Systems Aims and scope Submit manuscript

Abstract

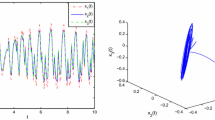
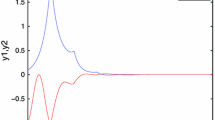
This paper mainly focuses on a novel H∞ control design to handle the global robust exponential stability problem for uncertain stochastic neutral-type neural networks (USNNNs) with mixed time-varying delays. Here the delays are assumed to be both discrete and distributed, which means that the lower and upper bounds can be derived. Firstly, we draw a control law for stabilized and stability of the neutral-type neural networks (NNNs). Secondly, by employing the Lyapunov-Krasovskii functional(LKF) theory, Jensen’s integral inequality, new required sufficient conditions for the global robust exponential stability of the given neural networks (NNs) are established in terms of delay-dependent linear matrix inequalities (LMIs), which can be easily checked in practice. The conditions obtained are expressed in terms of LMIs whose feasibility can be verified easily by MATLAB LMI control toolbox. Moreover, we have compared our work with previous one in the existing literature and showed that it reduces conservatism. Finally, one numerical example with their simulations is given to validate the effectiveness of our proposed theoretical results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. R. Sakthivel, R. Anbuvithya, K. Mathiyalagan, Y. K. Ma, and P. Prakash, “Reliable anti-synchronization conditions for BAM memristive neural networks with different memductance functions,” Applied Mathematics and Computation, vol. 275, pp. 213–228, 2016.

    Article  MathSciNet  Google Scholar 

  2. R. Sakthivel, M. Sathishkumar, B. Kaviarasan, and S. M. Anthoni, “Robust finite-time passivity for discrete-time genetic regulatory networks with Markovian jumping parameters,” Zeitschrift Naturforschung A, vol. 71, no. 4, pp. 289–304, 2016. [click]

    Google Scholar 

  3. X. Li and J. Wu, “Stability of nonlinear differential systems with state-dependent delayed impulses,” Automatica, vol. 64, pp. 63–69, 2016.

    Article  MathSciNet  MATH  Google Scholar 

  4. X. Zhang, G. Lu, and Y. Zheng, “Synchronization for timedelay Lur’e systems with sector and slope restricted nonlinearities under communication constraints,” Circuits, Systems, and Signal Processing, vol. 30, no. 6, pp. 1573–1593, 2011. [click]

    Article  MathSciNet  MATH  Google Scholar 

  5. M. Syed Ali, N. Gunasekaran, and Q. Zhu, “State estimation of fuzzy delayed neural networks with Markovian jumping parameters using sampled-data control,” Fuzzy Sets and Systems, vol. 306, pp. 87–104, 2017. [click]

    Article  MathSciNet  MATH  Google Scholar 

  6. J. Cao, D. Huang, and Y. Qu, “Global robust stability of delayed recurrent neural networks,” Chaos Solitons & Fractals, vol. 23, pp. 221–229, 2005.

    Article  MathSciNet  MATH  Google Scholar 

  7. X. Li and J. Cao, “An impulsive delay inequality involving unbounded time-varying delay and applications,” IEEE Transactions on Automatic Control, vol. 62, pp. 3618–3625, 2017.

    Article  MathSciNet  MATH  Google Scholar 

  8. M. Syed Ali, P. Balasubramaniam, and Q. Zhu, “Stability of stochastic fuzzy BAM neural networks with discrete and distributed time-varying delays,” International Journal of Machine Learning and Cybernetics, vol. 8, no. 1, pp. 263–273, 2017. [click]

    Article  Google Scholar 

  9. X. Li and J. Cao, “Delay-dependent stability of neural networks of neutral type with time delay in the leakage term,” Nonlinearity, vol. 23, no. 7, 2010.

    Google Scholar 

  10. R. Saravanakumar, M. Syed Ali, J. Cao, and H. Huang, “H state estimation of generalised neural networks with interval time-varying delays,” International Journal of Systems Science, vol. 47, no. 16, pp. 3888–3899, 2016.

    Article  MathSciNet  MATH  Google Scholar 

  11. X. Mao, X. Li, and J. Liu, “New robust stability criterion for neural networks of neutral type with time-varying delays,” Fourth International Conference on Natural Computation, 2008.

    Google Scholar 

  12. R. Rakkiyappan, Q. Zhu, and A. Chandrasekar, “Stability of stochastic neural networks of neutral type with Markovian jumping parameters: A delay-fractioning approach,” Journal of the Franklin Institute, vol. 351, no. 3, pp. 1553–1570, 2014.

    Article  MathSciNet  Google Scholar 

  13. B. Lee and J. Lee, “Robust stability and stabilization of linear delayed systems with structured uncertainty,” Automatica, vol. 35, no. 6, pp. 1149–1154, 1999. [click]

    Article  MathSciNet  MATH  Google Scholar 

  14. L. H. Xie, “Output feedback H control of systems with parameter uncertainty,” Int. J. Control, vol. 63, pp. 741–750, 1996.

    Article  MathSciNet  MATH  Google Scholar 

  15. R. Li and J. Cao, “Dissipativity analysis of memristive neural networks with time-varying delays and randomly occurring uncertainties,” Mathematical Methods in the Applied Sciences, vol. 39, no. 11, pp. 2896–2915, 2016.

    Article  MathSciNet  MATH  Google Scholar 

  16. W. Xie and Q. Zhu, “Mean square exponential stability of stochastic fuzzy delayed Cohen rossberg neural networks with expectations in the coefficients,” Neurocomputing, vol. 166, pp. 133–139, 2015. [click]

    Article  Google Scholar 

  17. H. Zhang, M. Dong, Y. Wang, and N. Sun, “Stochastic stability analysis of neutral-type impulsive neural networks with mixed time-varying delays and Markovian jumping,” Neurocomputing, vol. 73, pp. 2689–2695, 2010.

    Article  Google Scholar 

  18. F. Yao, J. Cao, P. Cheng, and L. Qiu, “Generalized average dwell time approach to stability and input-to-state stability of hybrid impulsive stochastic differential systems,” Nonlinear Analysis: Hybrid Systems, vol. 22, pp. 147–160, 2016.

    MathSciNet  MATH  Google Scholar 

  19. L. Liu and Q. Zhu, “Almost sure exponential stability of numerical solutions to stochastic delay Hopfield neural networks,” Applied Mathematics and Computation, vol. 266, pp. 698–712, 2015. [click]

    Article  MathSciNet  Google Scholar 

  20. X. Xiao, L. Zhou, D. Ho, and G. Lu, “Conditions for stability of linear continuous Markovian switching singular systems,” IET Control Theory & Applications, vol. 8, no. 3, pp. 168–174, 2014.

    Article  MathSciNet  Google Scholar 

  21. Y. Wu, Y. Wu, and Y. Chen, “Mean square exponential stability of uncertain stochastic neural networks with timevarying delay,” Neurocomputing, vol. 72, pp. 2379–2384, 2009.

    Article  Google Scholar 

  22. G. Zames, “Feedback and optimal sensitivity: Model reference transformations, multiplicative seminorms and approximate inverses,” IEEE Transactions on automatic control, vol. 26, no. 2, pp. 301–320, 1981. [click]

    Article  MathSciNet  MATH  Google Scholar 

  23. Y. Du, X. Li, and S. Zhong, “Robust reliable H control for neural networks with mixed time delays,” Chaos, Solitons and Fractals, vol. 91, pp. 1–9, 2016.

    Article  MathSciNet  Google Scholar 

  24. M. Ali and R. Saravanakumar, “Improved delay-dependent robust H control of an uncertain stochastic system with interval time-varying and distributed delays,” Chinese Physics B, vol. 23, no. 12, pp. 209–231, 2014. [click]

    Google Scholar 

  25. S. Lakshmanan, K. Mathiyalagan, J. H. Park, R. Sakthivel, and F. A. Rihan, “Delay-dependent H state estimation of neural networks with mixed time-varying delays,” Neurocomputing, vol. 129, pp. 392–400, 2014.

    Article  Google Scholar 

  26. K. Mathiyalagan, R. Anbuvithya, R. Sakthivel, J. H. Park, and P. Prakash, “Non-fragile H synchronization of memristor-based neural networks using passivity theory,” Neural Networks, vol. 74, pp. 85–100, 2016. [click]

    Article  Google Scholar 

  27. R. Saravanakumar, M. S. Ali, and M. Hua, “H state estimation of stochastic neural networks with mixed timevarying delays,” Soft Computing, vol. 20, no. 9, pp. 3475–3487, 2016.

    Article  MATH  Google Scholar 

  28. I. Stamova, T. Stamov, and X. Li, “Global exponential stability of a class of impulsive cellular neural networks with Supremums,” International Journal of Adaptive Control and Signal Processing, vol. 28, pp. 1227–1239, 2014.

    Article  MathSciNet  MATH  Google Scholar 

  29. E. Boukas and Z. Lin, Deterministic and Stochastic Time Delay Systems, Birkhauser, Boston, vol. 187, 2002.

  30. J. Park, “An analysis of global robust stability of uncertain cellular neural networks with discrete and distributed delays,” Chaos, Solitons & Fractals, vol. 32, no. 2, pp. 800–807, 2007.

    Article  MathSciNet  MATH  Google Scholar 

  31. M. Syed Ali, S. Arik, and R. Saravanakumar, “Delaydependent stability criteria of uncertain Markovian jump neural networks with discrete interval and distributed timevarying delays,” Neurocomputing, vol. 158, pp. 167–173, 2015. [click]

    Article  Google Scholar 

  32. X. Li, M. Bohner, and C. Wang, “Impulsive differential equations: Periodic solutions and applications,” Automatica vol.52, pp. 173–178, 2015.

    Google Scholar 

  33. Q. Zhou, X. Shao, J. Zhu, and H. Karimi, “Stability analysis for uncertain neural networks of neutral type with timevarying delay in the leakage term and distributed delay,” Abstract and Applied Analysis, vol. 2013, pp. 4339–4344, 2013.

    MATH  Google Scholar 

  34. Y. Fang, K. Li, and Y. Yan, “Novel robust exponential stability of Markovian jumping impulsive delayed neural networks of neutral-type with stochastic perturbation,” Mathematical Problems in Engineering, Article, vol. 3, pp. 1–20, 2016.

    Google Scholar 

  35. P. Balasubramaniam, G. Nagamani, and R. Rakkiyappan, “Global passivity analysis of interval neural networks with discrete and distributed delays of neutral type,” Neural Processing Letters, vol. 32, pp. 109–130, 2013.

    Article  Google Scholar 

  36. C. Y. Lu, “A delay-dependent approach to robust control for neutral uncertain neural networks with mixed interval time-varying delays,” Nonlinearity, vol. 24, pp. 1121–1136, 2011.

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Alagappa University, Karaikudi, 630 004, India

    Maharajan Chinnamuniyandi

  2. Ramanujan Centre for Higher Mathematics, Alagappa University, Karaikudi, 630 004, India

    Raja Ramachandran

  3. School of Mathematics, Southeast University, Nanjing, 211189, China

    Jinde Cao

  4. School of Electrical Engineering, Nantong University, Nantong, 226019, China

    Jinde Cao

  5. Department of Mathematics, Faculty of Science, Maejo University, Chiang Mai, Thailand

    Grienggrai Rajchakit

  6. School of Mathematics and Statistics, Shandong Normal University, Ji’nan, 250014, P. R. China

    Xiaodi Li

Authors
  1. Maharajan Chinnamuniyandi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Raja Ramachandran
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Jinde Cao
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Grienggrai Rajchakit
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Xiaodi Li
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jinde Cao.

Additional information

Recommended by Associate Editor Ohmin Kwon under the direction of Editor Jessie (Ju H.) Park. This work was jointly supported by the Rajiv Gandhi National Fellowship under the University Grant Commission, New Delhi with (Ref. No.F1-17.1/2016-17/RGNF-2015-17-SC-TAM-21509) and the Thailand research grant fund (RSA5980019) and Maejo University.

Maharajan Chinnamuniyandi received the B.Sc. degree in Mathematics from Alagappa Govt. Arts College affiliated to Alagappa University, Karaikudi in 2012, the M.Sc. and M.Phil. degrees in Mathematics from Alagappa University, Karaikudi, Tamilnadu, India, in 2014 and 2015, respectively. He was a recipient of University rank holder award in post graduation and also recipient of University rank holder award with gold medal in M. Phil. He is currently pursuing a Ph.D. degree in Alagappa University, Karaikudi, Tamilnadu, India. His current research interests include stability theory of neural networks, complex systems, fractional-order neural networks, stochastic and impulsive dynamical systems.

Raja Ramachandran received the M.Sc., M.Phil., and Ph.D. degrees in Mathematics from Periyar University, Salem, India, in 2005, 2006 and 2011, respectively. He served as a Guest faculty at Periyar University, India, after the completion of his doctoral studies. He was the recipient of Sir.C.V. Raman Budding Innovator Award for the year 2010 from Periyar University, India. He is currently working as an Assistant Professor in Ramanujan Centre for Higher Mathematics, Alagappa University, Karaikudi, India. He obtained a grant from UGC for distinguished Young Scientist Award for the year 2013. His research interests include fractional differential equations, neural networks, genetic regulatory networks, robust nonlinear control, stochastic systems, stability analysis of dynamical systems, synchronization and chaos theory. He has authored and coauthored for more than 40 publications in these research areas in Science Citation Indexed Journals. He was a member of the Editorial Board for two special issues in Mathematical Problems in Engineering and also he served as a reviewer for more than 20 SCI journals.

Jinde Cao is a Distinguished Professor, the Dean of School of Mathematics and the Director of the Research Center for Complex Systems and Network Sciences at Southeast University. From March 1989 to May 2000, he was with the Yunnan University. In May 2000, he joined the School of Mathematics, Southeast University, Nanjing, China. From July 2001 to June 2002, he was a Postdoctoral Research Fellow at the Department of Automation and Computer-Aided Engineering, Chinese University of Hong Kong, Hong Kong. Professor Cao was an Associate Editor of the IEEE Transactions on Neural Networks, the Journal of The Franklin Institute, Neurocomputing, and Differential Equations and Dynamical Systems. He is currently an Associate Editor of the IEEE Transactions on Cybernetics, the IEEE Transactions on Cognitive and Developmental Systems, the Neural Networks, Nonlinear Analysis: Modeling and Control, Mathematics and Computers in Simulation, the Advances in Difference Equations, and the Journal of Artificial Intelligence, and Soft Computing Research. He is a Fellow of IEEE, a Member of the Academy of Europe, and a Fellow of Pakistan Academy of Sciences. He has been named as Highly-Cited Researcher in Mathematics, Computer Science and Engineering by Thomson Reuters. He received the National Innovation Award in 2017.

Grienggrai Rajchakit received the Ph.D. degree in Applied Mathematics from KMUTT, Bangkok, Thailand. He served as a lecturer at Department of Mathematics Faculty of Science Maejo University, Chiangmai Thailand. He was the recipient of Thailand Frontier author Award by Thomson Reuters Web of Science in the year 2016. His research interests include differential equations, neural networks, robust nonlinear control, stochastic systems, stability analysis of dynamical systems, synchronization and chaos theory. He has authored and coauthored for more than 70 publications in these research areas. He was a reviewer for more than 20 journals.

Xiaodi Li was born in Shandong province, China. He received the B.S. and M.S. degrees from Shandong Normal University, Jinan, China, in 2005 and 2008, respectively, and the Ph.D. degree from Xiamen University, Xiamen, China, in 2011, all in applied mathematics. He is currently a Professor with the Department of Mathematics, Shandong Normal University. He has authored or coauthored more than 50 research papers. He is an Academic Editor of International Journal of Applied Physics and Mathematics (SG), Applications and Applied Mathematics (USA), and British Journal of Mathematics & Computer Science (UK). His current research interests include stability theory, delay systems, impulsive control theory, artificial neural networks, and applied mathematics.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Chinnamuniyandi, M., Ramachandran, R., Cao, J. et al. A New Global Robust Exponential Stability Criterion for H∞ Control of Uncertain Stochastic Neutral-type Neural Networks with Both Timevarying Delays. Int. J. Control Autom. Syst. 16, 726–738 (2018). https://doi.org/10.1007/s12555-017-0410-x

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12555-017-0410-x

Keywords

Search

Navigation