Skip to main content
SpringerLink
Log in

Trajectory linearization based output tracking control of an unmanned tandem helicopter with variance constraints

  • Regular Papers
  • Robotics and Automation
  • Published:
International Journal of Control, Automation and Systems Aims and scope Submit manuscript

Abstract

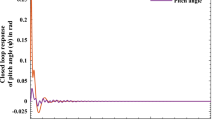
An output tracking control problem for an unmanned tandem rotor helicopter with variance constraints is investigated in this paper. A modified Trajectory Linearization Control (TLC) is proposed to stabilize a nonlinear continuous-time flight dynamics system of the tandem helicopter. The tracking controller structure of TLC is designed by using two-time-scale nonlinear dynamic inversion. The base control law of the translational and attitude loops is designed in a pseudo-inversion feedforward controller to deal with nonlinear features of the plant and a proportional integral controller to stabilize the linear slowly time-variant error system resulted from the nonlinear flight system. Furthermore, a feasible TLC strategy is designed to meet a performance index set including steady trajectory tracking error variance and desired Parallel D-spectrum (PD-) eigenvalues to achieve good flight quality. The Variance-constrained Trajectory Linearization Control (VCTLC) is designed to realize the desired steady tracking precision and agile capability. Flight simulation results show the VCTLC method is feasible and effective in attitude and altitude tracking.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Abbreviations

m, I i :

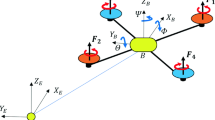
helicopter mass and inertial matrix, i = x, y, and z

Xf,rm, Yf,rm, Zf,rm:

forces generated by front/rear rotor

Lmr, Mmr , Nmr:

rotor moments in body frame

M=[LmMmNm]T:

torque on helicopter vector

hf, hr, l f , lr:

vertical and horizonal distances between gravity center and front/rear rotor’s center, see Fig. 1

Θ = [ϕθω]T:

helicopter angular position vector

P=[p e x p e y p e z ]T:

position vector relative to air in inertial frame

νb = [ν b x ν b y ν b z ]T:

body velocity vector

ωb = [p q r]T:

angular rate vector in body frame

LA, DA:

helicopter lift and drag

FH, FY, Qfm, Qrm:

horizontal force, side-force, and torques generated by front and rear rotor.

α, βs, acs:

angel of attack(AOA), slide angle(SA), and lift curve slope, respectively

λi, σs:

rotor inflow ratio and solidity ratio

µa, φ :

rotor advanced ratio and inflow angle

Ω, R :

rotor speed and radius

a0, rb:

coning angle, radius of blade element

b, \( \bar c \):

blade number and mean chord

δω=[δlatδlonδdir]T:

control inputs in longitudinal-, lateral-, and directional-direction respectively

θtw,θ p ,θ1s,θ1c:

rotor blade twist rate, rotor root collective pitch, and longitudinal/lateral cyclic pitch angle in wind axes respectively resuted from δ ω

Tf, Tr, Tm:

thrusts generated by front and rear rotors and their mean value respectively

ais , bis :

longitudinal and lateral tilt of tip path plane of the rotor with respect to shaft, i = f, r

ρa, d:

air density and stochastic disturbances

ωn, ζ:

plant natural frequency, damping ratio

f, r :

front- and rear- rotors

b, e, w, s :

in body, inertial frame and in wind, shaft axes, respectively

trim, ctrl, com:

in nominal control, error feedback and command input, respectively

\( \bar x,\tilde x \) :

nominal and error values of x

References

  1. S. Lee, C. Ha, and B. S. Kim, “Adaptive nonlinear control system design for helicopter robust command augmentation,” Aerospace Science and Technology, vol. 9, pp. 241–251, 2005.

    Article  MATH  Google Scholar 

  2. B. S. Kim and A. J. Calise, “Nonlinear flight control using neural networks,” Journal of Guidance, Control and Dynamics, vol. 20, no. 1, pp. 26–33, 1997.

    Article  MATH  Google Scholar 

  3. P. K. A. Menon, G. B. Chatterji, and V. H. L. Cheng, “Two-time scale autopilot for high performance aircraft,” Proc. of AIAA Guidance, Navigation and Control Conference, pp. 40–45, 1991.

  4. H. J. Lee, J. B. Park, and Y. H. Joo, “Comments on ‘output tracking and regulation of nonlinear system based on Takagi-Sugeno fuzzy model’,” IEEE Trans. on System, Man, and Cybernetics-part B: Cybernetics, vol. 33, no. 3, 521–523, June 2003.

    Article  Google Scholar 

  5. S. Esteban, J. Aracil, and F. Gordillo, “Lyapunov based asymptotic stability analysis of a three-time scale radio/control helicopter model,” Proc. of AIAA Atmospheric Flight Mechanics Conference, pp. 1–32, 2008.

  6. J. J. Zhu, Nonlinear Tracking and Decoupling by Trajectory Linearization, Dept. ECE, Louisiana State University, 1998.

  7. J. J. Zhu, “A note on extension of the eigenvalue concept,” IEEE Control Systems Magazine, vol. 13, no. 6, pp. 68–70, December 1993.

    Article  Google Scholar 

  8. Y. Liu, Neural Adaptive Nonlinear Tracking Using Trajectory Linearization, Ph.D. Dissertation, Ohio University, 2007.

  9. R. Huang, Y. Liu, and J. J. Zhu, “Guidance, navigation, and control system design for tripropeller vertical-takeoff- and- landing unmanned air vehicle,” Journal of Aircraft, vol. 46, no. 6, pp. 1837–1856, 2009.

    Article  Google Scholar 

  10. A. F. Hotz and R. E. Skelton, “A covariance control theory,” Int. Journal of Control, vol. 46. no. 1, pp. 13–32, 1987.

    Article  MATH  MathSciNet  Google Scholar 

  11. C.-H. Hu, J.-H. Zhu, X.-L. Huang, J.-C. Hu, and Z.-Q. Sun, “Output tracking of an unmanned tandem helicopter based on dynamic augment method,” Int. Journal of Control, Automation, and Systems, vol. 2, no. 2, pp. 156–164, 2004.

    Google Scholar 

  12. T. M. Adami, J. J. Zhu, A. K. Ishihara, and Y. H. Yeh, et al., “Six-DOF trajectory tracking for payload directed flight using trajectory linearization control,” Proc. of AIAA Guidance, Navigation and Control Conference, Seattle, Washington, pp. 1897–1916, 2009.

  13. A. J. Ostroff, D. R. Downing, and W. J. Rood, “A technique using a nonlinear helicopter model for determing trims and derivatives,” NASA Technical Note, TN D-8159, pp. 44–64, 1976.

  14. H. K. Khalil, Nonlinear Systems, 3rd Edition, Prentice Hall, New Jersey, 2002.

    MATH  Google Scholar 

  15. O. Tanner and H. P. Geering, “Two-degree-of freedom robust controller for an autonomous helicopter,” Proc. of the American Control Conference, Denver, Colorado, pp. 993–998, 2003.

  16. S. Barnett and C. Storey, “Analysis and synthesis of stability matrix,” Journal of Differential Equation, vol. 3, pp. 414, 1967.

    Article  MATH  MathSciNet  Google Scholar 

  17. B. Israel, A. Grevile, and T. N. E. Generalized Inverse: Theory and Application, John Willey and Sons, Inc., 1974.

Download references

Author information

Authors and Affiliations

  1. School of Aeronautics and Astronautics, Shanghai Jiao Tong University, Shanghai, 200240, China

    Shi-Qian Liu & Zhong-Liang Jing

  2. Department of Automation, Shanghai Jiao Tong University, Shanghai, 200240, China

    Jun-Guo Lu

Authors
  1. Shi-Qian Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jun-Guo Lu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Zhong-Liang Jing
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Shi-Qian Liu.

Additional information

Recommended by Editorial Board member Wen-Hua Chen under the direction of Editor Jae-Bok Song. This work was supported by the National Nature Science Foundation of P. R. China under Grant No. 10577012, the Aeronautical Science Foundation of China under Grant No. 20101757005, and the Shanghai Astronaut Foundation under Grant No. 09AA0303-4. The authors wish to thank the reviewers for their constructive comments and the editors for continuous encouragement. And thank Dr. Liang Zhu and Wei Shi in Shanghai Jiaotong University for giving much help.

Shi-qian Liu received his Ph.D. degree in Control Science and Engineering in 2003 from Nanjing University of Science and Technology. From January 2005 to March 2007, he was a postdoctoral researcher in the Department of Computer Science and Technology, Tsinghua University. He is currently an associate professor in the School of Aeronautics and Astronautics, Shanghai Jiao Tong University, China. His research interests are in the field of flight dynamics and control, nonlinear system, and automated UAVs.

Jun-Guo Lu received his Ph.D. degree in Control Theory and Control Engineering from Nanjing University of Science and Technology in 2001. From October 2001 to September 2003, he was with the Department of Automation, Shanghai Jiao Tong University as a Post-Doctoral Fellow. He is currently an associate professor in Department of Automation, Shanghai Jiao Tong University. His main research interest is in the field of chaos and complex system control, etc.

Zhong-liang Jing received his Ph.D. degrees in electronics and information technology from Northwestern Polytechnical University in 1994. He is currently Associate Dean, the Cheung Kong professor of Control Science and Engineering. From 1997 to 1998, he was a senior visiting scholar of the University of California at Berkeley. His research interests are information fusion, target tracking, etc.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Liu, SQ., Lu, JG. & Jing, ZL. Trajectory linearization based output tracking control of an unmanned tandem helicopter with variance constraints. Int. J. Control Autom. Syst. 8, 1257–1270 (2010). https://doi.org/10.1007/s12555-010-0611-z

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12555-010-0611-z

Keywords

Search

Navigation