Skip to main content
SpringerLink
Log in

Principle and Application of the Ball End Mill Tool Radius Compensation for NURBS Curve Swept Surfaces Based on 3-Axis CNC Milling Machines

  • Regular Paper
  • Published:
International Journal of Precision Engineering and Manufacturing Aims and scope Submit manuscript

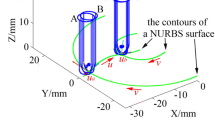
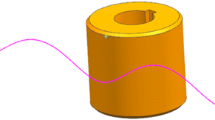
Abstract

Common 3-axis CNC milling machines are generally equipped with 2D tool radius compensation (2D-TRC), which can realize TRC function for the contours in three basic planes when flat end mills are used. The 2D-TRC function makes engineers to program according to the actual contour of a part, and avoids over-cut phenomenon. Unfortunately, the 2D-TRC is unsuitable for ball end mills (BEMs), especially in the situation of milling complex curves or surfaces. In this work, a new TRC named BEM-TRC is used for milling NURBS curve swept surfaces using BEMs based on 3-axis CNC milling machines. In BEM-TRC, the TRC of a BEM involves radial and axial compensation. The cutting point (CP), which is the tangent point between a BEM and a NURBS curve, is considered as a calculation basis point. After obtaining a CP on a NURBS curve using the equi-arc length bisection interpolation method, the cutter center point of a BEM is calculated through offsetting the CP the radius (r) distance of the BEM along its normal vector. Then the cutter location point of the BEM can be obtained according to the cutter center point. The CNC finishing program corresponding to the cutter location point can be obtained using Matlab software. The simulation based on VERICUT and machining based on a 3-axis milling machine verifies the effectiveness of the BEM-TRC. The over-cut phenomenon is avoided successfully when the BEM-TRC is used.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

References

  1. Yang, D. C. H., & Han, Z. (1999). Interference detection and optimal tool selection in 3-axis NC machining of free-form surfaces. Computer Aided Design, 31(5), 303–315.

    Article  Google Scholar 

  2. Chen, Z. C., & Cai, W. (2008). An efficient, accurate approach to representing cutter-swept envelopes and its applications to three-axis virtual milling of sculptured surfaces. Journal of Manufacturing Science and Engineering, 130(3), 031004.

    Article  Google Scholar 

  3. Wang, Z. Q., & Wang, X. R. (2014). The principle and application of cutting-point virtual tool radius compensation for ellipsoidal outer contour finishing using a ball end mill. The International Journal of Advanced Manufacturing Technology, 71(9–12), 1527–1537.

    Article  Google Scholar 

  4. Wang, T., & Chen, Y. (2011). Three-dimensional tool radius compensation for a 5-axis peripheral milling. Chinese Journal of Mechanical Engineering, 26(3), 3093–3096.

    Google Scholar 

  5. Qiao, Z., Liu, Z., Hu, M., Liu, L., Hu, W., & Ding, Y. (2019). A space cutter compensation method for multi-axis machining using triple NURBS trajectory. The International Journal of Advanced Manufacturing Technology, 103, 3969–3978.

    Article  Google Scholar 

  6. Zhou, X., Liu, X., Li, M., Wang, Z., & Meng, X. (2017). Post-processor development of a five-axis machine tool with optimization tool radius compensation. The International Journal of Advanced Manufacturing Technology, 88, 1505–1522.

    Article  Google Scholar 

  7. Zhou, B., Zhao, J., Li, L., & Xia, R. (2015). NURBS curve interpolation algorithm based on tool radius compensation method. International Journal of Production Research, 54(15), 4448–4474.

    Article  Google Scholar 

  8. Wang, F., Lin, H., Zheng, L., Liu, F., Yang, L., & Geng, C. (2013). A control algorithm for rapid movements near the radius compensation singularity in five-axis end milling. Journal of Systems Science and Complexity, 26, 718–734.

    Article  Google Scholar 

  9. Han, L., Gao, X.-S., & Li, H. (2013). Space cutter radius compensation method for free form surface end milling. The International Journal of Advanced Manufacturing Technology, 67, 2563–2575.

    Article  Google Scholar 

  10. Xu, R., & Chen, Z. (2014). Method of five-axis tool radius compensation based on post-processor. Journal of Mechanical Engineering, 50(13), 157–164.

    Article  Google Scholar 

  11. Xu, A., & Liu, N. (2011). Study on 3D cutter radius compensation technology based on direction vector. Machine Tool & Hydraulics, 39, 33–37.

    Google Scholar 

  12. Li, Z., Wang, Y., & Jin, Y. (2011). Research on 3D cutter radius compensation for 5-axis flank milling. Modular Machine Tool & Automatic Manufacturing Technique, 9, 1–3.

    Google Scholar 

  13. She, C. H., & Chang, C. C. (2006). Development of a 3D cutter compensation postprocessor system for multi-axis machining. Materials Science Forum, 505–507, 571–576.

    Google Scholar 

  14. Hong, H., Yu, D., & Zhang, L. (2009). Research on 3D cutter radius compensation for 5- axis end milling. China Mechanical Engineer, 20(15), 1770–1774.

    Google Scholar 

  15. Tung, C., & Tso, P. (2010). A generalized cutting location expression and postprocessors for multi-axis machine centers with tool compensation. The International Journal of Advanced Manufacturing Technology, 50(9–12), 1113–1123.

    Article  Google Scholar 

  16. Chen, Y., & Wang, T. (2013). Three-dimensional tool radius compensation for multi-axis peripheral milling. Chinese Journal of Mechanical Engineering, 26(3), 547–554.

    Article  Google Scholar 

  17. Chu, Z. Y., Ahn, I. H., & Seung, K. (2017). Process monitoring and inspection systems in metal additive manufacturing: Status and applications. International Journal of Precision Engineering and Manufacturing-Green Technology, 4(5), 235–245.

    Article  Google Scholar 

  18. Park, H. S., Dang, X. P., Nguyen, D. S., & Kumar, S. (2020). Design of advanced injection mold to increase cooling efficiency. International Journal of Precision Engineering and Manufacturing-Green Technology, 7(2), 319–328.

    Article  Google Scholar 

  19. Wang, X. R., Wang, Z. Q., Wang, Y. S., Wang, T. S., & He, P. (2017). A bisection method for the milling of NURBS mapping projection curves by CNC machines. The International Journal of Advanced Manufacturing Technology, 91(1–4), 155–164.

    Article  Google Scholar 

  20. Lin, B.-T., & Kuo, C.-C. (2009). Application of an integrated RE/RP/CAD/CAE/CAM system for magnesium alloy shell of mobile phone. Journal of Materials Processing Technology, 209(3), 2818–2830.

    Article  Google Scholar 

  21. Park, K., Kim, Y. S., Kim, C. S., & Park, H. J. (2007). Integrated application of CAD/CAM/CAE and RP for rapid development of a humanoid biped robot. Journal of Materials Processing Technology, 187–188, 609–613.

    Article  Google Scholar 

  22. Baek, D. K., Yang, S.-H., & Ko, T. J. (2012). Precision NURBS interpolator based on recursive characteristics of NURBS. The International Journal Advanced of Manufacturing Technology, 65(1–4), 403–410.

    Google Scholar 

  23. Lee, A.-C., Lin, M.-T., Pan, Y.-R., & Lin, W.-Y. (2011). The feedrate scheduling of NURBS interpolator for CNC machine tools. Computer Aided Design, 43(6), 612–628.

    Article  Google Scholar 

  24. Wang, X. R., Wang, Z. Q., Lin, T. S., & He, P. (2016). The high-energy micro-arc spark–computer numerical control deposition of planar NURBS curve coatings. The International Journal of Advanced Manufacturing Technology, 87(9–12), 3325–3335.

    Article  Google Scholar 

  25. Wu, J., Zhou, H., Tang, X., & Chen, J. (2015). Implementation of CL points preprocessing methodology with NURBS curve fitting technique for high-speed machining. Computers & Industrial Engineering, 81, 58–64.

    Article  Google Scholar 

  26. Caseiro, J. F., Valente, R. A. F., Reali, A., Kiendl, J., Auricchio, F., & Alves de Sousa, R. J. (2015). Assumed Natural Strain NURBS-based solid-shell element for the analysis of large deformation elasto-plastic thin-shell structures. Computer Methods in Applied Mechanics and Engineering, 284, 861–880.

    Article  MathSciNet  Google Scholar 

  27. Baek, D.-K., Ko, T.-J., & Yang, S.-H. (2012). Fast and precision NURBS interpolator for CNC systems. International Journal of Precision Engineering and Manfacturing, 13(6), 955–961.

    Article  Google Scholar 

  28. Chuang, S. H. F., & Shih, J. L. (2006). A novel approach for computing C2-continuous offset of NURBS curves. The International Journal of Advanced Manufacturing Technology, 29(1–2), 151–158.

    Article  Google Scholar 

  29. Piegl, L., & Tiller, W. (1997). The nurbs book. Berlin Heidelberg New York, New York: Springer-Verlag.

    Book  Google Scholar 

  30. Sun, Y., Bao, Y., Kang, K., & Guo, D. (2013). An adaptive feedrate scheduling method of dual NURBS curve interpolator for precision five-axis CNC machining. The International Journal of Advanced Manufacturing Technology, 68(9–12), 1977–1987.

    Article  Google Scholar 

Download references

Acknowledgements

This project is supported by National Natural Science Foundation of China (Grant no. 51465030), Employee innovation subsidy fund project of All China Federation of Trade Unions, Open project of State Key Laboratory of Advanced Welding and Joining (AWJ-21Z02), Gansu Science and Technology Planning Project (20YF8GA033, 17YF1GA018, 17CX1JA117, and 18JR3RA132), Western Young Scholars of Chinese Academy of Sciences, Lanzhou Talent Innovation and Entrepreneurship Project (2020-RC-120, 2019-RC-102, and 2018-RC-108), Longyuan Youth Innovative and Entrepreneurial Talents Project, Foundation of A Hundred Youth Talents Training Program of Lanzhou Jiaotong University, and Gansu Provincial Employee Technology Innovation Subsidy Fund Project.

Author information

Authors and Affiliations

  1. School of Mechatronic Engineering, Lanzhou Jiaotong University, Lanzhou, 730010, China

    Zhaoqin Wang, Xiaorong Wang, Xiaoqin Liu, Yusen Wang & Chengyu Li

  2. Key Laboratory of System Dynamics and Reliability of Rail Transport Equipment of Gansu Province, Lanzhou Jiaotong University, Lanzhou, 730010, China

    Zhaoqin Wang & Xiaorong Wang

  3. State Key Laboratory of Advanced Processing and Recycling of Nonferrous Metals, Lanzhou University of Technology, Lanzhou, 730050, China

    Zhaoqin Wang & Xiaorong Wang

  4. State Key Laboratory of Advanced Welding and Joining, Harbin Institute of Technology, Harbin, 150001, China

    Tiesong Lin & Peng He

Authors
  1. Zhaoqin Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xiaorong Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Xiaoqin Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Yusen Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Chengyu Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Tiesong Lin
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Peng He
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to Zhaoqin Wang or Xiaorong Wang.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wang, Z., Wang, X., Liu, X. et al. Principle and Application of the Ball End Mill Tool Radius Compensation for NURBS Curve Swept Surfaces Based on 3-Axis CNC Milling Machines. Int. J. Precis. Eng. Manuf. 22, 1517–1526 (2021). https://doi.org/10.1007/s12541-021-00555-5

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12541-021-00555-5

Keywords

Search

Navigation