Abstract
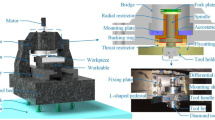
Dynamics modelling and simulating are the significant process to improve the machining accuracy of the machine tool. This paper is aimed to model and simulate the ultra-precision fly-cutting machine tool (UFMT) and find the relations between structure parameters and machined surface. In this paper, the multi-rigid-flexible-body dynamics model of the UFMT is firstly built by using transfer matrix method for multibody systems. After deducing overall transfer equation, overall transfer matrix, eigenfrequency equation and dynamics equations, the vibration characteristics and dynamics response of tool-tip are simulated and validated by tests. The machined surface is simulated by transferring displacement between the fly-cutting tool-tip and the workpiece into 3D curve. According to the simulation results, both the air-bearing stiffness of the flying-cutting head and cutting process parameters have effects on the machined surface.
















Similar content being viewed by others
Abbreviations
- \( {\varvec{Z}}_{i,j} \) :
-
State vector in modal coordinates
- \( {\varvec{z}}_{i,j} \) :
-
State vector in physical coordinates
- \( x,y,z \) :
-
Translational displacement in x, y, z physics coordinate
- \( X,Y,Z \) :
-
Translational displacement in x, y, z modal coordinate
- \( \theta_{x} ,\theta_{y} ,\theta_{z} \) :
-
Angular displacement in x, y, z physics coordinate
- \( \Theta_{x} ,\Theta_{y} ,\Theta_{z} \) :
-
Angular displacement in x, y, z modal coordinate
- \( m_{x} ,m_{y} ,m_{z} \) :
-
Internal torque in x, y, z physics coordinate
- \( M_{x} ,M_{y} ,M_{z} \) :
-
Internal torque in x, y, z modal coordinate
- \( q_{x} ,q_{y} ,q_{z} \) :
-
Internal force in x, y, z physics coordinate
- \( Q_{x} ,Q_{y} ,Q_{z} \) :
-
Internal force in x, y, z modal coordinate
- \( {\varvec{U}}_{\text{all}} \) :
-
Overall transfer matrix
- \( {\varvec{Z}}_{\text{all}} \) :
-
Overall state vector
- \( {\varvec{T}} \) :
-
Successive premultiplication of the transfer matrix of each element in the transfer paths from each tip to the root of the system
- \( {\varvec{G}} \) :
-
Successive premultiplication of the transfer matrix of each element in the transfer path from each tip to the k-th input end Ik of each body element which has multiple input ends
- \( {\varvec{v}} \) :
-
The translational and angular displacement column matrix
- \( {\varvec{M}},{\varvec{K}},{\varvec{C}} \) :
-
The mass, spring forces and damping forces matrix
- \( {\varvec{f}} \) :
-
The column matrix of external forces torques
- \( {\varvec{V}}^{k} \) :
-
Augmented eigenvector of k-order mode
- \( q^{k} \) :
-
Generalized coordinate for k-order mode
- \( \omega_{s} \) :
-
Natural frequency of s-order mode
- \( \zeta_{s} \) :
-
Damping proportion of s-order mode
- \( f_{z} \) :
-
The angular velocity of the spindle
- R :
-
The radius of the fly-cutting head
- \( z_{re} \) :
-
Relative displacements between the fly-cutting tool-tip and the workpiece surface in z-direction
References
Liang, Y., Chen, G., Sun, Y., Chen, J., Chen, W., & Nan, Y. U. (2014). Research status and outlook of ultra-precision machine tool. Journal of Harbin Institute of Technology,46(5), 28–39.
Zaeh, M., & Siedl, D. (2007). A new method for simulation of machining performance by integrating finite element and multi-body simulation for machine tools. CIRP Annals—Manufacturing Technology,56(1), 383–386.
Liang, Y. C., Chen, W. Q., Sun, Y. Z., Chen, G. D., Wang, T., & Sun, Y. (2012). Dynamic design approach of an ultra-precision machine tool used for optical parts machining. Proceedings of the Institution of Mechanical Engineers Part B-Journal of Engineering Manufacture,226(A11), 1930–1936. https://doi.org/10.1177/0954405412458998.
Liang, Y. C., Chen, W. Q., An, C. H., Luo, X. C., Chen, G. D., & Zhang, Q. (2014). Investigation of the tool-tip vibration and its influence upon surface generation in flycutting. Proceedings of the Institution of Mechanical Engineers Part C-Journal of Mechanical Engineering Science,228(12), 2162–2167. https://doi.org/10.1177/0954406213516440.
Wu, W. (2010). Extended transfer matrix method for dynamic modeling of machine tools. Journal of Mechanical Engineering,46(21), 69.
Zhang, M., Liu, Q., & Yuan, S. (2008). Machine tool spindle unit analysis system based on second development of ANSYS. Machine Tool & Hydraulics, 36(2), 11–16.
Yao, Y. F., Liu, Q., & Wen-Jing, W. U. (2011). Dynamic simulation of a linear motor feed drive system based on rigid-flexible & electrical-mechanical coupling. Journal of Vibration and Shock,30(1), 191–196.
Yang, X., An, C., Wang, Z., Wang, Q., Peng, Y., & Jian, W. (2016). Research on surface topography in ultra-precision flycutting based on the dynamic performance of machine tool spindle. International Journal of Advanced Manufacturing Technology,87(5–8), 1–9.
Rui, X., Wang, G., Lu, Y., & Yun, L. (2008). Transfer matrix method for linear multibody system. Multibody System Dynamics,19(3), 179–207.
Rui, X., Bestle, D., Zhang, J., & Zhou, Q. (2016). A new version of transfer matrix method for multibody systems. Multibody System Dynamics,38(2), 137–156.
Rui, X. T., Wang, X., Zhou, Q. B., & Zhang, J. S. (2019). Transfer matrix method for multibody systems (Rui method) and its applications. Science China-Technological Sciences,62(5), 712–720. https://doi.org/10.1007/s11431-018-9425-x.
Rui, X. T., Zhang, J. S., & Zhou, Q. B. (2014). Automatic deduction theorem of overall transfer equation of multibody system. Advances in Mechanical Engineering. https://doi.org/10.1155/2014/378047.
Rui, X., Wang, G. P., Zhang, J. S., Rui, X. T., & Sun, L. (2016). Study on automatic deduction method of overall transfer equation for branch multibody system. Advances in Mechanical Engineering,8(6), 16. https://doi.org/10.1177/1687814016651586.
Rui, X., Rong, B., Wang, G., & He, B. (2011). Discrete time transfer matrix method for dynamics analysis of complex weapon systems. Science China Technological Sciences,54(4), 1061–1071.
Rong, B., Rui, X., Wang, G., & Yu, H. (2011). Discrete time transfer matrix method for dynamic modeling of complex spacecraft with flexible appendages. Journal of Computational and Nonlinear Dynamics,6(1), 011013.
Chen, G. L., Rui, X. T., Abbas, L. K., Wang, G. P., Yang, F. F., & Zhu, W. (2018). A novel method for the dynamic modeling of Stewart parallel mechanism. Mechanism and Machine Theory,126, 397–412. https://doi.org/10.1016/j.mechmachtheory.2018.04.024.
Lu, H., Rui, X., & Chen, G. (2018). Study on the dynamics response of ultra-precision single-point diamond fly-cutting machine tool as multi-rigid-flexible-body system based on transfer matrix method for multibody systems. In 14th international conference on multibody systems, nonlinear dynamics, and control (vol. 6).
Chen, W. Q., Liang, Y. C., Sun, Y. Z., Huo, D. H., Su, H., & Zhang, F. H. (2015). A two-round design method for ultra-precision flycutting machine tools with stringent process requirements. Proceedings of the Institution of Mechanical Engineers Part B-Journal of Engineering Manufacture,229(9), 1584–1594. https://doi.org/10.1177/0954405414537248.
An, C., Deng, C., Miao, J., & Yu, D. (2018). Investigation on the generation of the waviness errors along feed-direction on flycutting surfaces. International Journal of Advanced Manufacturing Technology,96(1–4), 1457–1465.
Acknowledgements
The research was supported by Science Challenge Project (No. TZ2016006-0104).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Lu, H., Ding, Y., Chang, Y. et al. Dynamics Modelling and Simulating of Ultra-precision Fly-Cutting Machine Tool. Int. J. Precis. Eng. Manuf. 21, 189–202 (2020). https://doi.org/10.1007/s12541-019-00239-1
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12541-019-00239-1