Abstract
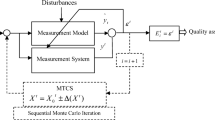
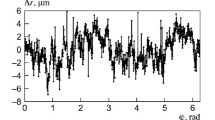
The paper presents a general algorithm for predictive metrological verification. The new algorithm is to be applied for dimensional control done with a measuring apparatus, regardless its area of use. Practically, the proposed method consists in a statistical analysis and a new interpretation for values what characterize the metrologca parameters: the accuracy error (scattering) and the precision error (fidelity). The theoretical studies and experimental researches were focused to identity the actual causes for the downgrading of the measuring apparatus due to normal wear. It was used a combination between statistical control parameters (the arithmetic mean and root-mean-square deviation (standard deviation)), and metrological characteristics (the accuracy error and precision error). The new algorithm for the predictive metrological verification allows the parameters dynamics observation. The user can forecast the evolution of the measuring apparatus qualitative characteristics. Thus, it can be discovered if the apparatus is damaged or simply it was taken out from its accuracy class due of normal wear.
Similar content being viewed by others
References
Baron, T., “Statistical Methods for Analysis and Quality Control of Production,” Didactic and Pedagogic Publishing, 1979.
Buzduga M., Marcuta C., and Sarbu G. C., “Metrology: Theory and Practice,” Technical–Info Publishing House, Chisinau, 2001. ISBN 9975-63-038-3 (in Romania)
Iliescu, C., Pantelimon, V., Cepisca, C., and Vlaicu, C., “Metrology. Measurement System,” ICPE Publishing, Bucharest, 1994. (in Romanian)
Taylor, J., “Introduction to Error Analysis, the Study of Uncertainties in Physical Measurements,” University Science Books, 1997.
Tiron, M., “Theory of Measurement Errors and the Least Squares Method,” Technical Publishing House, Bucharest, 1972.
IEEE Std. 1241-2010, “IEEE Standard for Terminology and Test Methods for Analog-To-Digital Converters,” 2001.
Bacivarov I. C., Bacivarov, A., and Mihalache A., “Statistical Control of Conformity and Products Reliability,” “Electronica 2000” Publishing House, Bucharest, 2003. ISBN 973-99878-6-9 (in Romania)
Chisci, L., Rossiter, J. A., and Zappa, G., “Systems with Persistent Disturbances: Predictive Control with Restricted Constraints,” Automatica, Vol. 37, No. 7, pp. 1019–1028, 2001.
Maciejowski, J. M., “Predictive Control: With Constraints,” Pearson Education, 2002.
Maeder, U., Borrelli, F., and Morari, M., “Linear Offset-Free Model Predictive Control,” Automatica, Vol. 45, No. 10, pp. 2214–2222, 2009.
Riaz, M. and Muhammad, F., “An Application of Control Charts in Manufacturing Industry,” Journal of Statistical and Econometric Methods, Vol. 1, No. 1, pp. 77–92, 2012.
Richards, A., “Fast Model Predictive Control with Soft Constraints,” European Journal of Control, Vol. 25, pp. 51–59, 2015.
NML CEE 73/362, “Measurements of Length,” 2001.
Official Journal of the European Union, “Regulation (EC) No 764/2008 of the European Parliament and of the Council,” 2008.
Montgomery, D. C., “Introduction to Statistical Quality Control,” Wiley, 6th Ed., 2009.
Nani, V., “Statistical Control of Processing Prismatic Pieces on Grinding Machines,” Measurement, Vol. 47, pp. 516–520, 2014.
Panaite, V. and Munteanu, R., “Statistical Control and Reliability,” Didactic and Pedagogical Publishing, 1982.
Ryan, T. P., “Statistical Methods for Quality Improvement,” Wiley, 2nd Ed., 2000.
Balestrieri, E., Catelani, M., Ciani, L., Rapuano, S., and Zanobini, A., “Word Error Rate Measurement Uncertainty Estimation in Digitizing Waveform Recorders,” Measurement, Vol. 46, No. 1, pp. 572–581, 2013.
Rao, C. V., Wright, S. J., and Rawlings, J. B., “Application of Interior-Point Methods to Model Predictive Control,” Journal of Optimization Theory and Applications, Vol. 99, No. 3, pp. 723–757, 1998.
Scokaert, P. O. and Mayne, D., “Min-Max Feedback Model Predictive Control for Constrained Linear Systems,” IEEE Transactions on Automatic control, Vol. 43, No. 8, pp. 1136–1142, 1998.
Vizireanu, D. N. and Preda, R. O., “Is “Five-Point” Estimation better than “Three-Point” Estimation?” Measurement, Vol. 46, No. 1, pp. 840–842, 2013.
Wills, A. G. and Heath, W. P., “An Exterior/Interior-Point Approach to Infeasibility in Model Predictive Control,” Proc. of 42nd IEEE Conference on Decision and Control, pp. 3701–3705, 2003.
Bemporad, A., Borrelli, F., and Morari, M., “Model Predictive Control Based on Linear Programming~ The Explicit Solution,” IEEE Transactions on Automatic Control, Vol. 47, No. 12, pp. 1974–1985, 2002.
Ling, K.-V., Wu, B. F., and Maciejowski, J., “Embedded Model Predictive Control (MPC) Using a FPGA,” IFAC Proceedings Volumes, Vol. 41, No. 2, pp. 15250–15255, 2008.
Wang, Y. and Boyd, S., “Fast Model Predictive Control Using Online Optimization,” IEEE Transactions on Control Systems Technology, Vol. 18, No. 2, pp. 267–278, 2010.
Wills, A. G. and Heath, W. P., “Barrier Function Based Model Predictive Control,” Automatica, Vol. 40, No. 8, pp. 1415–1422, 2004.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Nani, VM. A New Algorithm for Predictive Metrological Verification of Measuring Apparatus. Int. J. Precis. Eng. Manuf. 19, 167–172 (2018). https://doi.org/10.1007/s12541-018-0019-x
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12541-018-0019-x