Skip to main content
SpringerLink
Log in

Pull-in instability analysis of electrostatically actuated microplate with rectangular shape

  • Published:
International Journal of Precision Engineering and Manufacturing Aims and scope Submit manuscript

Abstract

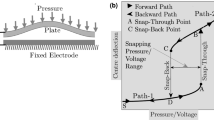
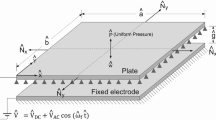
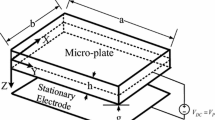
As the size of the micro-electro-mechanical systems (MEMS) continues to decrease, the classical elasticity continuum theory may be inefficient to describe their mechanical behaviors. By introducing the strain gradient elasticity into the classical Kirchhoff plate theory, the size-dependent model for electrostatically actuated microplate-based MEMS is developed. The sixth-order partial differential equation (PDE), derived with the help of the principle of minimum potential energy, can be numerically solved by utilizing generalized differential quadrature (GDQ) method and pseudo arc-length algorithm. The model, with three material length scale parameters (MLSPs) included, can predict prominent size-dependent normalized pull-in voltage with the reduction of characteristic structural size, especially when the plate dimension is comparable to the MLSP (on the order of microns). This study may be helpful to characterize the mechanical properties of electrostatically actuated MEMS, or guide the design of microplate-based devices for a wide range of potential applications.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Abbreviations

a :

length of the micro-plate

b :

width of the micro-plate

h :

thickness of the micro-plate

g :

gap between two electrodes

w(x,y) :

the transverse displacement along Z axis

\(\bar u\) :

the strain energy density

ɛ ij :

the strain tensor

ɛ′ ij :

the deviatoric strain

γ i :

the dilatation gradient tensor

η (1) ijk :

the deviatoric stretch gradient tensor

ξ s ij :

the symmetric rotation gradient tensor

∂ i :

the differential operator

u i :

the displace-ment vector

ɛ mm :

the dilatation strain

η s ijk :

the symmetric part of the second order displacement gradient tensor

δ ij :

Knocker delta

e ijk :

the permutation tensor

σ ij :

stress tensor

p i , τ (1) ijk , m s ij :

the higher-order stresses

k :

the bulk modulus

µ:

shear modulus

l 0, l 1, l 2 :

the additional independent MLSPs

ɛ :

the dielectric constant of the gap medium

x i , y i :

grid coordinates in X and Y directions

N, M :

grid number in X and Y directions

c (m) ik :

the weighting factors for the approximation of the m-th order derivative of the i-th point in the X direction

{ie1085-2}:

the weighting factors for the approximation of the m-th order derivative of the j-th point in the Y direction

s :

size effect

References

  1. Chao, P. C. P., Chiu, C. W. and Tsai, C. Y., “A novel method to predict the pull-in voltage in a closed form for micro-plates actuated by a distributed electrostatic force,” Journal of Micromechanics and Microengineering, Vol. 16, No. 5, pp. 986–998, 2006.

    Article  Google Scholar 

  2. Younis, M. I., Abdel-Rahman, E. M. and Nayfeh, A., “A reduced-order model for electrically actuated microbeam-based MEMS,” Journal of Microelectromechanical Systems, Vol. 12, No. 5, pp. 672–680, 2003.

    Article  Google Scholar 

  3. Batra, R. C., Porfiri, M. and Spinello, D., “Electromechanical model of electrically actuated narrow microbeams,” Journal of Microelectromechanical Systems, Vol. 15, No. 5, pp. 1175–1189, 2006.

    Article  Google Scholar 

  4. Nayfeh, A. H., Younis, M. I. and Abdel-Rahman, E. M., “Dynamic pull-in phenomenon in MEMS resonators,” Nonlinear Dynamics, Vol. 48, No. 1–2, pp. 153–163, 2007.

    Article  MATH  Google Scholar 

  5. Nayfeh, A. H. and Younis, M. I., “Modeling and simulations of thermoelastic damping in microplates,” Journal of Micromechanics and Microengineering, Vol. 14, No. 12, pp. 1711–1717, 2004.

    Article  Google Scholar 

  6. Zhao, X. P., Abdel-Rahman, E. M. and Nayfeh, A. H., “A reduced-order model for electrically actuated microplates,” Journal of Micromechanics and Microengineering, Vol. 14, No. 7, pp. 900–906, 2004.

    Article  Google Scholar 

  7. Machauf, A., Nemirovsky, Y. and Dinnar, U., “A membrane micropump electrostatically actuated across the working fluid,” Journal of Micromechanics and Microengineering, Vol. 15, No. 12, pp. 2309–2316, 2005.

    Article  Google Scholar 

  8. Mukherjee, S., Bao, Z. P., Roman, M. and Aubry, N., “Nonlinear mechanics of MEMS plates with a total Lagrangian approach,” Computers & Structures, Vol. 83, No. 10–11, pp. 758–768, 2005.

    Article  Google Scholar 

  9. Batra, R. C., Porfiri, M. and Spinello, D., “Reduced-order models for microelectromechanical rectangular and circular plates incorporating the Casimir force,” International Journal of Solids and Structures, Vol. 45, No. 11–12, pp. 3558–3583, 2008.

    Article  MATH  Google Scholar 

  10. Lam, D. C. C. and Chong, A. C. M., “Indentation model and strain gradient plasticity law for glassy polymers,” Journal of Materials Research, Vol. 14, No. 9, pp. 3784–3788, 1999.

    Article  Google Scholar 

  11. Lam, D. C. C., Yang, F., Chong, A. C. M., Wang, J. and Tong, P., “Experiments and theory in strain gradient elasticity,” Journal of the Mechanics and Physics of Solids, Vol. 51, No. 8, pp. 1477–1508, 2003.

    Article  MATH  Google Scholar 

  12. McFarland, A. W. and Colton, J. S., “Role of material microstructure in plate stiffness with relevance to microcantilever sensors,” Journal of Micromechanics and Microengineering, Vol. 15, No. 5, pp. 1060–1067, 2005.

    Article  Google Scholar 

  13. Nix, W. D., “Mechanical properties of thin films,” Metallurgical Transactions A-.Physical Metallurgy and Materials Science, Vol. 20, No. 11, pp. 2217–2245, 1989.

    Article  Google Scholar 

  14. Fleck, N. A., Muller, G. M., Ashby, M. F. and Hutchinson, J. W., “Strain gradient plasticity: theory and experiment,” Acta Metallurgica Et Materialia, Vol. 42, No. 2, pp. 475–487, 1994.

    Article  Google Scholar 

  15. Poole, W. J., Ashby, M. F. and Fleck, N. A., “Micro-hardness of annealed and work-hardened copper polycrystals,” Scripta Materialia, Vol. 34, No. 4, pp. 559–564, 1996.

    Article  Google Scholar 

  16. Chasiotis, I. and Knauss, W. G., “The mechanical strength of polysilicon films: Part 2. Size effects associated with elliptical and circular perforations,” Journal of the Mechanics and Physics of Solids, Vol. 51, No. 8, pp. 1551–1572, 2003.

    Article  Google Scholar 

  17. Aifantis, E. C., “Exploring the applicability of gradient elasticity to certain micro/nano reliability problems,” Microsystem Technologies-Micro-and Nanosystems-Information Storage and Processing Systems, Vol. 15, No. 1, pp. 109–115, 2009.

    Google Scholar 

  18. Yang, J., Jia, X. L. and Kitipornchai, S., “Pull-in instability of nano-switches using nonlocal elasticity theory,” Journal of Physics D: Applied Physics, Vol. 41, No. 3, Paper No. 035103, 2008.

  19. Kong, S. L., Zhou, S. J., Nie, Z. F. and Wang, K., “Static and dynamic analysis of micro beams based on strain gradient elasticity theory,” International Journal of Engineering Science, Vol. 47, No. 4, pp. 487–498, 2009.

    Article  MATH  MathSciNet  Google Scholar 

  20. Wang, B., Zhao, J. and Zhou, S., “A micro scale Timoshenko beam model based on strain gradient elasticity theory,” European Journal of Mechanics — A/Solids, Vol. 29, No. 4, pp. 591–599, 2010.

    Article  Google Scholar 

  21. Wang, B., Zhou, S., Zhao, J. and Chen, X., “Size-dependent pull-in instability of electrostatically actuated microbeam-based MEMS,” J. Micromech. Microeng., Vol. 21, No. 2, Paper No. 027001, 2011.

  22. Mindlin, R. D., “Second Gradient of Strain and Surface-Tention in Linear Elasticity,” International Journal of Solids and Structures, Vol. 1, pp. 417–438, 1965.

    Article  Google Scholar 

  23. Osterberg, P. M. and Senturia, S. D., “M-TEST: A test chip for MEMS material property measurement using electrostatically actuated test structures,” Journal of Microelectromechanical Systems, Vol. 6, No. 2, pp. 107–118, 1997.

    Article  Google Scholar 

  24. Kuang, J. H. and Chen, C. J., “Dynamic characteristics of shaped micro-actuators solved using the differential quadrature method,” Journal of Micromechanics and Microengineering, Vol. 14, No. 4, pp. 647–655, 2004.

    Article  Google Scholar 

  25. Papargyri-Beskou, S. and Beskos, D. E., “Static, stability and dynamic analysis of gradient elastic flexural Kirchhoff plates,” Archive of Applied Mechanics, Vol. 78, No. 8, pp. 625–635, 2008.

    Article  MATH  Google Scholar 

  26. Shu, C. and Richards, B. E., “Parallel simulation of incompressible viscous flows by generalized differential quadrature,” Computing Systems in Engineering, Vol. 3, No. 1–4, pp. 271–281, 1992.

    Article  Google Scholar 

  27. Shu, C., “Generalized differential-integral quadrature and application to the simulation of incompressible viscous flows including parallel computation,” Ph.D. Thesis, University of Glasgow, 1991.

  28. Shu, C. and Richards, B. E., “Application of generalized differential quadrature to solve two-dimensional incompressible Navier-Stokes equations,” International Journal for Numerical Methods in Fluids, Vol. 15, No. 7, pp. 791–798, 1992.

    Article  MATH  Google Scholar 

  29. Shu, C. and Du, H., “A generalized approach for implementing general boundary conditions in the GDQ free vibration analysis of plates,” International Journal of Solids and Structures, Vol. 34, No. 7, pp. 837–846, 1997.

    Article  MATH  Google Scholar 

  30. Rabinowitz, P. H., “Applications of Bifurcation Theory: proceedings of an advanced seminar,” Academic Press Inc., pp. 215–237, 1977.

  31. Leissa, A. W., “The free vibration of rectangular plates,” Journal of Sound and Vibration, Vol. 31, No. 3, pp. 257–293, 1973.

    Article  MATH  Google Scholar 

  32. Kim, K. S., Chang, H. S. and Akhter, N., “Determination of Poisson’s Ratio of a Beam by Time-Average ESPI and Euler-Bernoulli Equation,” Int. J. Precis. Eng. Manuf., Vol. 11, No. 6, pp. 979–982, 2010.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Civil Engineering, Shandong University, Jinan, Shandong, 250061, China

    Binglei Wang & Junfeng Zhao

  2. Department of Earth and Environmental Engineering, Columbia University, New York, NY, 10027, USA

    Binglei Wang & Xi Chen

  3. School of Mechanical Engineering, Shandong University, Jinan, Shandong, 250061, China

    Shenjie Zhou & Junfeng Zhao

  4. School of Aerospace, Xi’an Jiaotong University, Xi’an, 710049, China

    Xi Chen

  5. Department of Civil & Environmental Engineering, Hanyang University, Seoul, Korea, 133-791

    Xi Chen

Authors
  1. Binglei Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Shenjie Zhou
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Junfeng Zhao
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Xi Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Shenjie Zhou.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Wang, B., Zhou, S., Zhao, J. et al. Pull-in instability analysis of electrostatically actuated microplate with rectangular shape. Int. J. Precis. Eng. Manuf. 12, 1085–1094 (2011). https://doi.org/10.1007/s12541-011-0145-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12541-011-0145-1

Keywords

Search

Navigation