Abstract
In this study, the effect of kinetic energy of the shot peening process on microstructure, mechanical properties, residual stress, fatigue behavior and residual stress relaxation under fatigue loading of AISI 316L stainless steel were investigated to figure out the mechanisms of fatigue crack initiation and failure. Varieties of experiments were applied to obtain the results including microstructural observations, measurements of hardness, roughness, induced residual stress and residual stress relaxation as well as axial fatigue test. Then deep learning approach through neural networks was used for modelling of mechanical properties and fatigue behavior of shot peened material. Comprehensive parametric analyses were performed to survey the effects of different key parameters. Afterward, according to the results of neural network analysis, further experiments were performed to optimize and experimentally validate the desirable parameters. Based on the obtained results the favorable range of shot peening coverage regarding improved mechanical properties and fatigue behavior was identified as no more than 1750% considering Almen intensity of 21 A (0.001 inch).
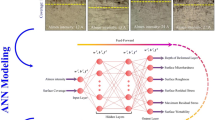
Graphic abstract

Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Fatigue failure mostly initiates from the surface layer of the components [1,2,3]. Therefore, applying severe plastic deformation (SPD) methods such as shot peening (SP) have critical role for surface and structural integrity of the materials [2, 5,6,7,8,9,9]. Tow parameters of Almen intensity and surface coverage are specified as the main parameters of SP process [10, 11]. Beneficial effects of conventional shot peening (CSP) and severe shot peening (SSP) which has higher severity than CSP (by increasing the values of intensity and coverage) were studied on improvement of mechanical properties and fatigue behavior of the different metallic materials in the last decade. The results indicate that SSP has higher positive effects than CSP which caused by inducing of higher compressive residual stress and nanocrystallization of the surface layer grains [8, 12,13,14,15,16,17,18]. However, over shot peening (OSP) which induces higher kinetic energy than SSP has detrimental influence on surface of the target material. OSP create surface defects such as overlaps and nano/micro cracks [19,20,21]. It was reported that fatigue life reduces after performing OSP compared to the severely and/or conventionally shot peened material [22,23,24]. Determination of the boundary between SSP and OSP and therefore finding the maximum optimal conditions of SP is quite challenging. Maleki et al. [25] presented some experimental approaches for specification of the boundaries between CSP, SSP and OSP. Although the presented methods works, but because of their fully experimental nature, they are time and cost consuming.
On the other hand, artificial intelligence (AI) based methods such as neural networks (NN) are remarkably applied in different aspects of science and engineering [26,27,28,29], as well as their applications in fatigue behavior prediction and analysis [30,31,32,33,34,35] and modelling of SP process [28, 30, 36,37,38]. In general, a neural network has three major layers of input, hidden and output [39]. Shallow neural network (SNN), as the primary generation of artificial neural networks, were mostly used in simulation of different processes. SNN has 1 or 2 hidden layers which generally trained by back-propagation (BP) algorithm [40]. These networks besides their beneficial applications have some limitations. The most important limitation of SNNs is the large number of data set required for their development [41]. Considering the improvements achieved in the developing of NNs by deep learning methods including restricted Boltzmann machine (RBM) and deep belief network (DBN) presented by Hinton et al. [42, 43] in 2006, it is feasible to develop deep neural network (DNN) using greedy layer-wised pre-training. After further improvements in this area, other alternative methods for pre-training of DNN such as stacked auto-encoder (SAE) were presented which helps to develop DNN with small data set and achieve higher efficiency by increasing the number of hidden layers and using SAE in between them [44,45,46,47].
In the present study, effects of different SP treatments with various severities were investigated on the microstructure, mechanical properties and axial fatigue behavior of the AISI 316L stainless steel. In addition, circumstance of residual stresses relaxation due to fatigue loading and initiation of the fatigue crack growth were studied experimentally. Then different NNs including SNN, DNN and SAE assigned DNN (SADNN) were developed for modelling of the distribution of hardness and residual stress from top surface to interior, residual stress relaxation and fatigue behavior. The developed NNs were assessed and the optimum structures were selected for parametric analyses. Afterward, based on the obtained results of NNs, further experiments were accomplished to optimize and experimental validation of the desirable parameters as well as the specification of the boundary between the SSP and OSP.
2 Experimental
2.1 Materials and Specimens
Fatigue test specimens of AISI 316L SS were prepared according to the ASTM E466 [48] standard using sheets of mechanically ground and polished material with mirror finishing. The chemical composition of the AISI 316L SS is C 0.22, Mn 1.34, Si 0.47, Cr 17.11, Cu 0.41, Mo 2.03, Ni 10.15, Co 0.26, P 0.034, S 0.005 and the remainder is Fe (in wt%). Shape and dimensions of the fatigue test specimens are shown in Fig. 1.
2.2 Shot Peening Treatments
Four different SP treatments with identical Almen intensity of 21 A (0.001 inch) and coverages of 100, 1500, 2500 and 3000% were performed on the specimens. Almen intensity was achieved according to SAE J443 standard on the A Almen strips [49]. Standard steel shots with average diameter and hardness of 0.58 mm and 50 HRC respectively were used. SP treatments performed with perpendicular impact direction and the distance between nozzle outlet and surface of the specimens was about 10 cm.
2.3 Microstructural Observations
Optical microscopy (OM) and field emission scanning electron microscopy (FESEM) were accomplished on the cross-sectioned samples using Olympus and Mira 3-XMU, respectively. Samples were impregnated in a Phenolic hot mounting resin and ground with a series of SiC papers up to P4000. Then samples were polished by polycrystalline diamond water-based suspensions and etched with Marble solution for 5 s.
2.4 XRD Crystallite Size Measurements
XRD measurements were performed for the determination of the grain size after applying SP treatments. For XRD analysis, X’Pert PRO MPD (PANalytical) X-ray diffractometer and X’Pert High Score Plus (V. 3) analyzer which associated with MATLAB R2015b were employed with CuKα radiation operating at 40 kV and 40 mA, scanning angles of 30º–150º, and irradiating an area of 10 mm. The full width at half maximum (FWHM) of the diffraction θ peaks were also obtained and the crystallite sizes were calculated using using Williamson–Hall (W–H) method [50, 51].
2.5 Microhardness Measurements
Vickers microhardness measurements were carried out from surface up to 650 µm depth using Qness GmbH Q30 A microhardness tester with a diamond Vickers indenter at a load of 10 gf for a duration of 7 s. The measurements were accomplished along three parallel paths from shot peened surface with same depth for each measurement through the core material and average of them were reported.
2.6 Surface Roughness Measurements
Before roughness measurements, samples were cleaned by means of acetone and distilled water in an ultrasound bath for 10 min per each step and then they were dried with warm air. Surface roughness was measured using SURFCORDER SE500 based on the definition of ISO 4287 [52]. Measurements were applied on three random areas of each sample and the average values were reported.
2.7 Residual Stress Measurements
The distribution of residual stresses was assessed using XRD analysis by means of Xstress 3000 G2/G2R X-ray Stress Analyzer (radiation Cr Kα, λKα1 = 2.2898 Å, irradiated area of 4 mm diameter, sin2ψ method, and diffraction angle (2θ) ~ 156 scanned between 45 and − 45). Measurements were carried out from surface to depth of 320 µm by removing a very thin layer of material with 40 µm thickness via electro-polishing with a solution of acetic acid (94%) and perchloric acid (6%).
2.8 Fatigue Test
Fatigue behavior of the as-received (AR) and shot peened specimens were studied using SANTAMSAF 250 axial fatigue test equipment with frequency of 30 Hz and stress ratio of R = 0.1. Fatigue tests performed at room temperature and air relative humidity of 50%. 20 samples were used to obtain S–N curves in each series and average fatigue life of two different specimens was reported in each stress amplitude. Only for the stress amplitude of 320 MPa, four samples of each series were used and average of them was reported.
3 Neural Networks
Inspired from performance of human’s brain, NNs are widely used for understanding complex problems and presenting logical solutions by means of functional relation [53,54,55][56]. NNS can be employed for modeling and analysis of non-linear processes which have different effective parameters [57]. Schematic architecture of a single layer NN fed with r and s number of input p and output a parameters respectively, with corresponded weight matrixes w, bias vectors b, linear combiner u and transfer function f, is presented in Fig. 2a. The methodology considered in this study is presented in Fig. 2b. Several SNNs and DNNs were developed via trial and error approach as there in no exact formula to obtain high performance NN. In the collected data, 80% of them were considered for training and the remained 20% samples were regarded in order to test and evaluate the developed network structures. Random selection of data was used for training and testing processes. Performance assessment of the networks was determined in terms of the accuracy of the predicted results of NNS which calculated by means of correlation coefficient (R2). R2 can be calculated as follows [58]:
where, n is the number of fed samples, fEXP and fANN represent the experimental and predicted values respectively. The values of FEXP and FANN are determined as follows:
Figure 3a illustrates a typical SNN with two hidden layers. It is well know that number of neurons as computational nodes of NNs and the number of layers in a NN have critical role on the performance of modelling. Number of neurons is one of the major variable parameters of the network structure. Oftentimes, by increasing the number of neurons the performance of the NN is rising as well although it makes the computational time longer.
Figure 3b illustrates architecture of a DDN schematically which is a modified SNN with more hidden layers and structurally they are so similar. DNN can be developed with or without pre-training process. In the presented image, SAE is assigned to DNN for pre-training. SAE is corresponded in between each layers of DNN. Therefore to construct SADNN with j layers and full inter-connection, j − 1 SAEs are employed and for the presented model with total 6 layers consist of [input layer-4 hidden layers-output layer], 5 SAEs are utilized. Considering the number of layers and neurons, 6 layers SADNN with L–(M–N–O–P)–Q structure, has 5 SAEs which have structures of L–(M)–L, M–(N)–M, N–(O)–N, O–(P)–O and P–(Q)–P.
Circumstance of assigning SAE to DNN according to number of neurons in each layer of DNN is shown in the right part of the Fig. 3b. The number of neurons in each SAE is similar to ones used in corresponded DNN layers. First SAE catches the input fed to DNN as its particular inputs and outputs data and after processing them the achieved outputs in its hidden layer are transferred to the second SAE as the new particular inputs and outputs. This process continues till to reach to the last SAE. After successfully training of SAEs, obtained initial weights and biases values of each layer wj(0), are assigned to DNN's corresponding layer to initialize the modelling process with fine-tuned SADNN.
Figure 3c–e shows the three different considered models in the present study. Modelling A is used for investigation of the effects of SP severity on distribution of microhardness and residual stress as outputs and depth from surface and surface coverage as inputs. In modelling B, besides the used inputs of modelling A, fatigue cycles in terms of fatigue life in particular stress amplitude is added to get the residual stress relaxation as output. Finally, in modelling C, parameters of surface coverage and stress amplitude are considered as inputs for modelling of fatigue life as output.
In the implementation of the NNs, based on the three considered models of A, B and C, different SNNs, DNNs and SADNNs were developed.
After achieving optimum structures of NNs with highest performance, chain rule based relation on the values of weights and biases are implemented to generate principle model function considering the results obtained in whole layers. For example the model function of modelling C considering 6 layers network can be determined as follows:
where a1, a2, a3, a4 and a5are the outputs of the first to fifth layers respectively. The function M assigns the values of the 2 considered input parameters of surface coverage and stress amplitude to the output parameter of fatigue life m(1).
4 Results and Discussions
4.1 Experimental Results
OM observations of the shot peened specimens with × 300 magnifications are shown in Fig. 4a that reveals the grain refinement in the surface layer of the treated materials which generated gradient structures. Also, it can be observed that by increasing the surface coverage, depth of the plastically deformed layer induced by SP is enhanced. Li et al. [59] classified engineering materials to structural and chemical gradient materials. Based on the mentioned category, shot peened materials are placed in the grain size structural gradients. Figure 4b, depicts the schematic illustration of a shot peened specimen under the applied force of axial fatigue test with considering the applied force axis on the magnified part of the specimen.
In order to achieve the crystallite size (after applying severe plastic deformation by using coverages of 1500, 2500 and 3000%) on the surface of the SP treated samples, XRD analysis were performed and the crystallite sizes were calculated. Figure 5 depicts the XRD patterns of AR and shot peened samples in different diffraction angle intervals. It can be observed that peak height of the AR sample was slightly decreased after applying SP and the decreasing trend became more notable as the severity of the treatments increased. AR sample primary consists of γ -austenite phase about 96.8% (in volume) and α-martensite phase about 3.2% (in volume). The amounts of α phase were increased up to 5.9, 11.3, 11.8 and 12.1% after applying SP treatments in the shot peened samples with 100, 1500, 2500 and 3000% due to the high extent of induced deformation. Related information obtained from XRD analysis for the three highest peaks in the high severity shot peened samples are illustrated in Table 1. It can be seen that by increasing of the surface coverage, the crystallite sizes on the top surface are decreasing down to 22.7 ± 0.5, 21.8 ± 0.5 and 21.1 ± 0.5 nm for the shot peened samples with coverage of 1500, 2500 and 3000% respectively and the materials are become nano-structured. The average grain size of the AR sample was determined as 110 ± 5 µm by stereological methods based on the OM observations. Moreover, to find out the grain size in the shot peened sample with 100% coverage, a very thin layer of top treated surface was polished and etched for OM characterization and the average grain size was measured as 65 ± 5 µm.
Figure 6a represents microhardness profiles of the AR and shot peened specimens. By increasing coverage caused by enhancing of peening duration and therefore rising of SP severity, microhardness is increased as well especially in the shot peened surface. From CSP with 100% coverage to SSP with 1500% coverage, the surface microhardness enhanced significantly up to about 22%. Distribution of induced residual stress as a function of distance from the treated surface is shown in Fig. 6b. It can be observed that by applying SSP treatments, considerable compressive residual stresses (CRSs) are induced in depth of the material due to the high energy impacts. However, by increasing coverage maintaining the same intensity, induced CRSs in the surface are not improved significantly and almost remain stable. Similar findings have been reported with analogous SP treatments on other metallic materials as well [60,61,62,63].
a Microhardness profiles of the AR and treated samples from top surface towards the core material. b Distributions of the induced residual stresses in the AR and shot peened samples. c S–N curves of the AR and shot peened samples. d Residual stress distributions at different number of cycles under 320 MPa stress amplitude in the shot peened specimens with 1500, 2500 and 3000%
Surface roughness as a well-established side effect of SP treatment was measured. The average roughness values in terms of Ra are obtained as 3.43, 3.62, 3.65, and 3.60 µm for the treatments with 100, 1500, 2500 and 3000% respectively (roughness of AR sample: 1.88 µm). The results indicate that by enhancing coverage, firstly roughness of material is raised and then remained in a stable range. Figure 6c reveals the obtained S–N curves of all series. Fatigue behavior is improved in the shot peened samples with 100 and 1500% coverage. However, in the specimens treated with 2500 and 3000% which have higher plastically deformed layer, detrimental effects of SP can be seen and they were over-shot peened. CRSs relaxation was investigated in the fatigued specimens treated with 1500, 2500 and 3000% coverage at different cycles of 1, 0.5 Nf and 0.7 Nf under 320 MPa stress amplitude (see Fig. 6d).
Almost half of the CRSs in the surface of the treated samples are released after 1st cycle and rate of CRS relaxation is decreased in the next cycles. Trend of CRSs relaxion in first cycle was reported similarly in previous studies [64, 65]. In addition, maximum CRSs in the depth of the treated samples with 1500% coverage are released more than those with 2500 and 3000% coverages in both 0.5 Nf and 0.7 Nf cycles as well as the first cycle.
It was observed that although treated specimens with 2500 and 3000% coverages had higher plastically deformed layer and a little bit higher CRSs in the initial state and lower CRSs relaxation in the fatigued conditions, these two SP treatments have detrimental effects on fatigue behavior. Also based on the OM observations no clear defects were seen on these samples. Therefore, FESEM observations with higher magnifications of × 3000–15,000 were applied to specify the generated defects caused by OPS.
Figure 7a, c and e depict the cross-sectional FESEM images of shot peened samples with 1500, 2500 and 3000% coverages. Generated micro-cracks in the surface of the treated specimens with 2500 and 3000% coverages can be clearly observed in the surface which confirms the OSP. By increasing severity in the OSP, length and number of the generated surface micro-cracks are increased. Nano-structured (NS) and ultrafine-grained (UFG) layers in the severely shot peened specimen with 1500% coverage are illustrated in Fig. 7a (left) with higher magnification of ×15,000. Figures 7b, d and f show the effects of applying axial fatigue load in the fatigued specimens at 0.5 Nf under 320 MPa stress amplitude. No fatigue crack initiation and/or growth is seen in the severely shot peened specimen with ×6000 magnification up to its the half of fatigue life. However, in the over-shot peened samples generated micro-cracks in the surface are grown in the crack opening direction caused by force axis at 0.5 Nf clearly.
4.2 Modelling Results
In order to obtain the structure of NN with highest performance and in order to compare the efficiency of SNN, DNN and SADNN various networks with different architecture and network parameters were developed for each considered modelling of A, B and C. In whole models logarithmic sigmoid (logsig) transfer functions were used in hidden and output layers and constant rate of training of 0.195 was gathered. The digital data used for implementation of NNs are presented in Appendix. Accuracy of the results of constructed SNNs with 1 and 2 hidden layers with different number of neurons in terms of considered output parameters of the three different models of A, B and C is shown in Fig. 8a, c and e (the results of Fig. 8a and b were presented in terms of output parameter of microhardness in modelling A). It can be observed that in developing SNNs, mostly by increasing the number of neurons, the performance of the network is enhancing as well. In Fig. 8b, d and f comparison of the accuracy of the developed SNNs, DNNs and SADNNs predicted with highest performance is presented. In all of the developed NNs for modelling A and C, 2 and 1 neurons were used in input and output layers respectively and in the developed NNs for modelling B, 3 and 1 neurons were used in input and output layers jointly. It can be observed that, by implementation of a SADNN in 4 hidden layers network which has the highest performance among whole developed NNs, accuracies of 0.99 were obtained for both training and testing processes that is quite acceptable. Details of the developed network performance evaluation are presented in Table 2.
In order to survey the overfitting and performance independency of the obtained optimum structure for each models of A, B and C from the used data fed to the network, repeated random sub-sampling cross validation (also known as Monte Carlo cross-validation) is applied. Three more orders of data set were generated using random function to select the other data for training and testing (80% samples for training and 20% samples for testing). Performance evaluations of the other randomly selected data are shown in Table 3 (In model A, the results are presented in terms of output parameter of microhardness). It can be observed that in the whole considered randomly derived data sets, like the one already used, accuracies of at least 0.99 and 0.98 were obtained for training and testing processes, respectively.
After successful cunstructing of the SADNN with highest performnce and accuray, related model fucations of each considered models of A, B and C were generated for parametric analysis to figure out the influence of each process paramters on the desired outputs. Figure 9 represents the results of the predicted values of parameric analysis in terms of surface coverage and deth of surface to the interior on the microhardness and induced residuals stresses. It can be observed that by increasing the coverage, depth of the enhanced hardness is rising as well altough form about 1500% coverage the values of microhardness on top surface (depth of zero) are remained quasi stable (see Fig. 9a). These results have high agreement with the presnted OM observations of plastically deformed layer in Fig. 4a. Also a sudden jump can be seen after 1000% coverage from microhardness of about 400 to 440 Hv. In Fig. 9b the distribution of the induced residual stresses in depth can be seen clearly by vartions of coverage. It can be observed that, in depth of about 70–80 µm the highest amounts of CRSs are induced after surface coverage of about 750%. Also the the obtained results of NNs clearly show the effects of low surface coverages between 0 to 100%; from 0 to 100% the values induced CRSs, gradually increase from 10 MPa to about − 250 MPa. In addition after about 225 µm depth, the SP process has not remarkable effects in inducing of CRSs. Figure 10 reveals the circumstance of CRSs relaxation in different surface coverages of 1500, 2500 and 3000%. Similar to experiments, it can be seen that in the OSP treated samples with 2500 and 3000% coverage, lower CRSs relacation occurred compared tho the severly shot peened sample with 1500% coverage by increasing of the relevant fatigue life cycles. This phenomenon depicts that, the stresses amplitudue due to axial fatigue loading are mostly used for crack propagation of the existance micro-cracks of the OSP samples rather than employing for CRSs relaxation which makes the high amount of induced residual stresses useless. These results indicatade that absence of surface defects are more important than inducing high CRSs under condition of axial fatigue loading.
Finally, as one of the major aims of this study, in Fig. 11, the paramteric analysis in terms of surface coverage and stress amplitued for prediction of fatigue life is presnted using obtaiend results of NNS from modelling C. It can be seen that by decreasing the stress amplitue as a parameter of fatigue test, the numbrer of cycles to failure are rising in each coverages. Considering fatigue life of 4.5 × 106 cycles as maximum fatigue life (Nf,max) and run-out factor, fatigue life of 3.3 × 106 cycles (presented with yellow color in the countor) has about 0.7 Nf,max. By following of the 0.7 Nf,max in the countor in the related interval of 220–290 MPa stress amplitued, it can be observed that the variation of fatigue life has three main stages. Firstly, by increasing surface coverage from about 250 to 1000% the fatigue life is enhancing gradually as well. Secondly, from SP coverage of about 1000 to 1700%–1800% the fatigue life is quasi stable. Finally, by increasing surface coverage from about 1700–1800 to 3000% the fatigue life is reducing significently which indicates the detrimental effects of OSP (see Fig. 11b). The experimnetal data used for development of modelling C, only had results of fatigue life for different coverages of 100, 1500, 2500 and 3000%. Also, the the microstructural observations showed that applied SP treatments with 2500 and 3000% coverages have signs of the OSP. However, the obtained results of NNs reavel that OSP occurred in lower coverage than 2500% and also the posetive effects of SSP still can be seen upto surface covergae of about 1700%–1800% which is more than the experimntal data of 1500%. In the next section authenticity of the predited results by NNs will be assessed experimentally.
5 Experimental Validation and Specifying the Boundary Between SSP and OSP
In order to validate the authenticity of obtained results of NNS for fatigue life variation and specifying the boundary between SSP and OSP in the shot peened 316L steel with Almen intensity of 21 A, three more SP treatments with coverages of 1750, 2000 and 2250% were performed. Surface microhardness and residual stress measurements were accomplished as well as axial fatigue. Figure 12a, illustrates the measured properties on the samples. It can be observed that as the difference of coverage between them are not high; the values of surface microhardness and residual stresses have not considerable differences. However, fatigue limit is decreased in the shot peened specimens with 2000 and 2250% coverages which indicate that they are over-shot peened. The fatigue limit in the shot peened sample with 1750% is increased compared to treated one with 1500%. The fatigue behavior results show that highest coverage for applying SSP with 21 A in the considered SP is 1750%. In addition, similar behavior in the CRSs relaxation is observed in the severely shot peened sample with 1750% and over-shot peened ones with 2000 and 2250% compared to the firstly performed SP treatments.
Figure 12b, indicates the obtained fatigue lives of the all treated samples in comparison with AR samples in the same stress amplitude of 320 MPa. From CSP (SP with 100% coverage) to SSP (SP with coverages up to 1750%) the average fatigue life is increased significantly. However, in the over-shot peened samples with 2000 and 2250% fatigue life decreased compared to severely treated samples and in the OSP treatments with coverages of 2500 and 3000% the fatigue life reduced in comparison with conventionally treated one. The obtained experimental results of fatigue tests approved the authenticity of obtained results of NNs for fatigue life variation which indicated after about 1700%–1800% coverage the OSP can be occurred.
In addition, Fig. 13 reveals FESEM images of the fatigued specimens at 320 MPa stress amplitude and 0.7 Nf after applying SP treatments with 1750, 2000 and 2250% coverages. Fatigue cracks are initiated beneath and from the surface layer in the severely and over- shot peened samples respectively (Fig. 13a, c) which can be another approval for the authenticity of obtained results of NNs. Also, in the over-shot peened sample with 2000% coverage, generated micro-cracks are grown from surface in the NS layer and some other cracks are initiated under the surface. The initiation of fatigue crack are mostly shown by observing the fracture surface (fractography) after fatigue failure, but in this study, to the best of authors knowledge, the fatigue crack initiation in a shot peened material with fatigued condition and not totally failed is presented for the first time using cross-sectional view.
Figure 14 illustrates the OM image of the treated specimen with 1750% coverage that distribution of the CRSs and also depth of each generated layers after grain refinement are shown on it schematically. Depth of the generated NS, UFG and refined grains layers after SSP were approximately measured by high magnification FESEM observations. Based on the obtained results, fatigue cracks initiated beneath the NS and UFG layers about 15 µm from the surface. By comparison with CRSs distribution, it can be observed that in the crack initiation site, the values of induced CRSs are close to their maximum. As there is no defect or micro-crack in the NS surface, the cracks must initiated under the surface layer which has high CRSs. Therefore, it can be deduced that firstly most of the applied energy by fatigue test to undergo fracture is used to decrease and release the CRSs and secondly the remained energy is used for both crack initiation and CRSs relaxation. This phenomenon caused higher CRSs relaxation in the severely shot peened samples compared to the over-shot peened materials. In the over-shot peened samples as the micro-cracks already exist in the surface, most of the applied energy is directly used for micro-crack growth which caused lower CRSs relaxation and faster fatigue failure. It is notable to mention that in the investigation of the crack initiation and growth, identical stress of 320 MPa was applied on all the severely and over-shot peened specimens that generate same energy to have better comparison.
By applying SSP and enhancing its severity, which resulted in generation of gradient structures in the surface layer from NS to refined grains, roughness alteration, microhardness improvement and inducing CRSs, cracks initiation and growth are delayed which caused fatigue behavior improvement. In the OSP, based on the total fatigue life relation which is equal to the summation of the number of cycles for the crack initiation and propagation, although SP has effects on mechanical properties improvement, existing of generated defects in the surface, remarkably reduced the required cycles for crack initiation. Therefore, after applying OSP, the fatigue life is decreased compared to CSP and SSP which indicates its detrimental influence on fatigue behavior.
According to the all mentioned above, schematic illustration of the AR and generated gradient structures in the treated surfaces with CSP and SSP processes is presented in Fig. 15a based on the microstructural observations in this study and the previous studies [66,67,68,69,70]. Also, presentation of the crack initiation sites in the treated material with SSP and OSP is shown in Fig. 15b schematically.
6 Conclusion
In this study different types of shot peening including conventional, severe and over shot peening processes were applied on 316L stainless steel. Effects of treatments were investigated through several experiments including microstructural characterization, measurements of microhardness, surface roughness and residual stress as well as axial fatigue test. Also, residual stress relaxation and fatigue crack initiation were assessed in the fatigued samples. Then the achieved experimental data used for developing there different neural networks using deep learning approach and also the stacked auto-encoder for pre-training. Correlation coefficient as a parameter of accuracy was considered for networks performance evaluation. The networks assessment results indicated that by using stacked auto-encoder assigned deep neural network very high accuracy of more than 0.99 can achieved in both training and testing process for the whole constructed models. In addition, in order to assess the authenticity of obtained results of neural networks and also to optimize the SP process and finding the boundary between SSP and OSP, further experimental validations were performed which approved the predicted results. These outcomes reveal that deep learning approach can be used as an alternative method to pave the path for modelling of the complex and non-linear phenomena such as fatigue behavior using small data set. Overall, based on the obtained experimental and modelling results it can be concluded that:
-
Gradient structures from nano-structured to refined grains were generated in the surface layer by increasing the severity of shot peening compared to the conventional treatment.
-
By increasing coverage and thus enhancing the shot peening kinetic energy, remarkable improvement in mechanical properties can be obtained.
-
Due to the grain refinement, microhardness improvement and high compressive residual stresses, crack initiation and growth were delayed resulting in fatigue strength improvement.
-
In the severely shot peened material, firstly most of the applied energy caused by fatigue loading is used to release the induced compressive residual stresses and then the remained energy is used for crack initiation and residual stresses relaxation.
-
In the over-shot peened material, the required number of cycles for crack initiation was significantly reduced due to generation of micro-cracks in the surface after high shot impacts which resulted detrimental influence on fatigue behavior.
-
Most of the applied energy of fatigue loading was directly used for micro-crack growth in resulted in lower compressive residual stresses relaxation.
-
In the shot peening of 316L steel with Almen intensity of 21A [0.001 inch], surface coverage of 1750% has the maximum beneficial effects on fatigue behavior improvement.
-
The absence of surface defects such as micro-cracks are more important than inducing high compressive residual stresses and increasing the surface layer hardness by grain refinement, under condition of axial fatigue loading for life improvements.
References
S. Bagherifard, M. Guagliano, Eng. Fract. Mech. 81, 56 (2012)
A. Amanov, R. Karimbaev, E. Maleki, O. Unal, Y.-S. Pyun, T. Amanov, Surf. Coat. Tech. 358, 695 (2019)
E. Maleki, N. Maleki, A. Fattahi, O. Unal, M. Guagliano, S. Bagherifard, Surf. Coat. Tech. 405, 126729 (2021)
Y. Efe, I. Karademir, F. Husem, E. Maleki, R. Karimbaev, A. Amanov, O. Unal, Appl. Surf. Sci. 528, 146922 (2020)
A. Tevlek, H.M. Aydın, E. Maleki, R. Varol, O. Unal, Surf. Coat. Tech. 366, 204 (2019)
E. Maleki, O. Unal, Optimization of shot peening effective parameters on surface hardness improvement. Met. Mater. Int. (2020). https://doi.org/10.1007/s12540-020-00758-x
Y. Lv, L. Lei, L. Sun, Mater. Sci. Eng. A 658, 77 (2016)
E. Maleki, S. Bagherifard, M. Bandini, M. Guagliano, Addit. Manuf. 37, 101619 (2021)
B. Sagbas, Met. Mater. Int. 26, 143 (2020)
M. Guagliano, J. Mater. Process. Tech. 110, 277 (2001)
O. Unal, E. Maleki, Measurement 125, 133 (2018)
S. Pour-Ali, A.-R. Kiani-Rashid, A. Babakhani, S. Virtanen, M. Allieta, Surf. Coat. Tech. 334, 461 (2018)
R. Karimbaev, Y.-S. Pyun, E. Maleki, O. Unal, A. Amanov, Mater. Sci. Eng. A 791, 139752 (2020)
M. Jayalakshmi, P. Huilgol, B.R. Bhat, K.U. Bhat, Surf. Coat. Tech. 344, 295 (2018)
E. Maleki, O. Unal, K.R. Kashyzadeh, Mater. Charact. 157, 109877 (2019)
G.H. Farrahi, J.L. Lebrijn, D. Couratin, Fatigue Fract. Eng. M. 18, 211 (1995)
C. Liu, H. Zheng, X. Gu, B. Jiang, J. Liang, J. Alloy. Compd. 770, 500 (2019)
C. Zhang, M. Zheng, Y. Wang, P. Gao, B. Gan, Surf. Coat. Tech. 378, 124821 (2019)
B. Gentil, M. Desvignes, L. Castex, Mater. Tech. 75, 493 (1987)
Y. Wang, H. Xie, Z. Zhou, X. Li, W. Wu, J. Gong, Int. J. Hydrogen Energ. 45, 7169 (2020)
C. Yang, Y.G. Liu, M.Q. Li, Appl. Surf. Sci. 509, 144711 (2020)
M. Benedetti, T. Bortolamedi, V. Fontanari, F. Frendo, Int. J. Fatigue 26, 889 (2004)
R. Fathallah, A. Laamouri, H. Sidhom, C. Braham, Int. J. Fatigue 26, 1053 (2004)
E. Maleki, O. Unal, K.R. Kashyzadeh, Surf. Coat. Tech. 344, 62 (2018)
E. Maleki, O. Unal, A. Amanov, Surf. Interf. 13, 233 (2018)
N. Maleki, S. Kashanian, E. Maleki, M. Nazari, Biochem. Eng. J. 128, 1 (2017)
E. Maleki, N. Maleki, J. Electron. Mater. 45, 3822 (2016)
E. Maleki, O. Unal, Met. Mater. Int. 27, 262 (2021)
E. Maleki, G.H.H. Farrahi, Int. J. Eng. Trans. B Appl. 31, 382 (2018)
E. Maleki, O. Unal, K. Reza Kashyzadeh, Int. J. Fatigue 116, 48 (2018)
E. Maleki, O. Unal, Fatigue limit prediction and analysis of nano-structured AISI 304 steel by severe shot peening via ANN. Eng. Comput. (2020). https://doi.org/10.1007/s00366-020-00964-6
H. Alqahtani, S. Bharadwaj, A. Ray, Eng. Fail. Anal. 119, 104908 (2021)
S.N.S. Mortazavi, A. Ince, Comput. Mater. Sci. 185, 109962 (2020)
J.F. Barbosa, J.A.F.O. Correia, R.C.S.F. Júnior, A.M.P. Deesus, Int. J. Fatigue 135, 105527 (2020)
D.Z. Li, W. Wang, F. Ismail, Eng. Appl. Artif. Intel. 57, 153 (2017)
E. Maleki, G.H. Farrahi, K. Reza Kashyzadeh, O. Unal, M. Gugaliano, S. Bagherifard, Effects of conventional and severe shot peening on residual stress and fatigue strength of steel AISI 1060 and residual stress relaxation due to fatigue loading: experimental and numerical simulation. Met. Mater. Int. (2020). https://doi.org/10.1007/s12540-020-00890-8
C. Karataş, A. Sozen, E. Dulek, Expert Syst. Appl. 36, 3514 (2009)
L. Shahid, F. Janabi-Sharifi, Neural Comput. Appl. 31, 4829 (2019)
M. Jahanshahi, E. Maleki, A. Ghiami, Neural Comput. Appl. 28, 3209 (2017)
E. Maleki, Mater. Today 3, 2197 (2016)
D.J. Livingstone, D.T. Manallack, I.V. Tetko, J. Comput. Aid. Mol. Des. 11, 135 (1997)
G.E. Hinton, S. Osindero, Y.-W. Teh, Neural Comput. 18, 1527 (2006)
G.E. Hinton, R.R. Salakhutdinov, Science 313, 504 (2006)
Y. Bengio, P. Lamblin, D. Popovici, H. Larochelle, in Advances in Neural Information Processing Systems 19, ed. by B. Schölkopf, J. Platt, T. Hofmann. NIPS'06: 19th International Conference on Neural Information Processing Systems, Vancouver, 4-7 December 2006. (MIT Press, Cambridge, 2007), p. 153
S. Feng, H. Zhou, H. Dong, Mater. Design 162, 300 (2019)
G. Liu, H. Bao, B. Han, Math. Probl. Eng. 2018, 5105709 (2018)
Y.B. Wang, Z.H. You, X. Li, T.H. Jiang, X. Chen, X. Zhou, L. Wang, Mol. Biosyst. 13, 1336 (2017)
ASTM E466–15, Practice for Conducting Force Controlled Constant Amplitude Axial Fatigue Tests of Metallic Materials (ASTM International, West Conshohocken, 2015)
SAE J443_201006, Procedures for Using Standard Shot Peening Almen Strip (SAE International, Warrendale, 2010)
T. Das, A. Erdogan, B. Kursuncu, E. Maleki, O. Unal, Surf. Coat. Tech. 406, 126383 (2020)
D.L. Dorset, Microsc. Microanal. 4, 513 (1998)
ISO 4287:1997, Geometrical Product Specifications (GPS)—Surface texture: profile method—Terms, definitions and surface texture parameters (International Organization for Standardization, Geneva, 1997)
E. Maleki, M.J. Mirzaali, M. Guagliano, S. Bagherifard, Surf. Coat. Tech. 408, 126782 (2020)
B. Eren, M.A. Guvenc, S. Mistikoglu, Met. Mater. Int. 27, 193 (2021)
A.F.A. El-Rehim, D.M. Habashy, H.Y. Zahran, H.N. Soliman, Mathematical modelling of Vickers hardness of Sn–9Zn–Cu solder alloys using an artificial neural network. Met. Mater. Int. (2021). https://doi.org/10.1007/s12540-020-00940-1
T. Thankachan, K.S. Prakash, V. Kavimani, S.R. Silambarasan, Met. Mater. Int. 27, 220 (2021)
E. Maleki, G.H. Farrahi, K. Sherafatnia, in Machining, Joining and Modifications of Advanced Materials. Advanced Structured Materials, vol. 61, ed. by A. Öchsner, H. Altenbach (Springer, Singapore, 2016), pp. 45–60
E. Maleki, IOP Conf. Ser. Mat. Sci. 103, 012034 (2015)
X. Li, L. Lu, J. Li, X. Zhang, H. Gao, Nat. Rev. Mater. 5, 706 (2020)
Q. Lin, H. Liu, C. Zhu, R.G. Parker, Appl. Surf. Sci. 489, 66 (2019)
S. Bagherifard, R. Ghelichi, M. Guagliano, Appl. Surf. Sci. 259, 186 (2012)
E. Maleki, O. Unal, Surf. Interf. 11, 82 (2018)
L. Xie, C. Wang, L. Wang, Z. Wang, C. Jiang, W. Lu, V. Ji, Mech. Mater. 99, 2 (2016)
K. Zhan, C.H. Jiang, V. Ji, Mater. Trans. 53, 1578 (2012)
J.-C. Kim, S.-K. Cheong, H. Noguchi, Int. J. Fatigue 55, 147 (2013)
S. Bagherifard, S. Slawik, I. Fernández-Pariente, C. Pauly, F. Mücklich, M. Guagliano, Mater. Design 102, 68 (2016)
E.R. de los Rios, A. Walley, M.T. Milan, G. Hammersley, Int. J. Fatigue 17, 493 (1995)
Y.K. Gao, X.R. Wu, Acta Mater. 59, 3737 (2011)
E.R. De Los Rios, M. Trull, A. Levers, Fatigue Fract. Eng. M. 23, 709 (2000)
E. Maleki, O. Unal, K.R. Kashyzadeh, Met. Mater. Int. 25, 1436 (2019)
Funding
Open access funding provided by Politecnico di Milano within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Maleki, E., Unal, O., Guagliano, M. et al. Analysing the Fatigue Behaviour and Residual Stress Relaxation of Gradient Nano-Structured 316L Steel Subjected to the Shot Peening via Deep Learning Approach. Met. Mater. Int. 28, 112–131 (2022). https://doi.org/10.1007/s12540-021-00995-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12540-021-00995-8