LMBOPT: a limited memory method for bound-constrained optimization

Abstract

Recently, Neumaier and Azmi gave a comprehensive convergence theory for a generic algorithm for bound constrained optimization problems with a continuously differentiable objective function. The algorithm combines an active set strategy with a gradient-free line search CLS along a piecewise linear search path defined by directions chosen to reduce zigzagging. This paper describes LMBOPT, an efficient implementation of this scheme. It employs new limited memory techniques for computing the search directions, improves CLS by adding various safeguards relevant when finite precision arithmetic is used, and adds many practical enhancements in other details. The paper compares LMBOPT and several other solvers on the unconstrained and bound constrained problems from the CUTEst collection and makes recommendations on which solver to use and when. Depending on the problem class, the problem dimension, and the precise goal, the best solvers are LMBOPT, ASACG, and LMBFG-EIG-MS.

1 Introduction

The bound constrained optimization problem (BCOPT) is the task of minimizing a function subject to a feasible region defined by simple bounds on the variables. In this paper we describe the implementation and numerical evaluation of a new active set method for solving the bound constrained optimization problem

$$\begin{aligned} \begin{array}{ll} \min &{} f(x)\\ \text {s.t. } &{} x\in {\mathbb {R}}^n,~~~\underline{x}\le x\le \overline{x}, \end{array} \end{aligned}$$

(1)

where $\mathbf{x}=[\underline{x},\overline{x}]$ is a bounded or unbounded box in ${\mathbb {R}}^n$ describing the bounds on the variables and the objective function $f:\mathbf{x}\rightarrow {\mathbb {R}}$ is continuously differentiable with gradient

$$\begin{aligned} g(x){:}{=}\partial f(x)/\partial x\in {\mathbb {R}}^n. \end{aligned}$$

Problems with naturally given bounds appear in a wide range of applications including the optimal design problem [4], contact and friction in rigid body mechanics [51], the obstacle problem [54], journal bearing lubrication and flow through a porous medium [49]. Often variables of an optimization problem can only be considered meaningful within a particular interval [31]. Some approaches [1] reduce the solution of variational inequalities and complementarity problems to bound constrained problems. The bound constrained optimization problem also arises as an important subproblem in algorithms for solving general constrained optimization problems based on augmented Lagrangians and penalty methods. Numerous research papers [17, 27, 38, 39, 52] deal with the development of efficient numerical algorithms for solving bound constrained optimization problems, especially when the number of variables is large.

1.1 Past work

In the last few years, many algorithms have been developed for solving the BCOPT problem (1).

Active set methods are among the most effective methods. They consist of two main stages that alternate until a solution is found. In the first stage one identifies a good approximation for the set of optimal active bound constraints, defining a face likely to contain a stationary point of the problem. A second stage then explores this face of the feasible region by approximately solving an unconstrained subproblem.

A classical reference for active set methods for bound constrained problems with a convex quadratic objective function (QBOPT) is the projected conjugate gradient method of Polyak [56], which drops and adds only one constraint in each iteration. That is, at each step of this active set method, the dimension of the subspace of active variables is changed by one. This fact implies that if there are $n_1$ constraints active at the starting point $x^0$ and $n_2$ constraints active on the solution of QBOPT, we need at least $|n_2-n_1|$ iterations to reach the solution of QBOPT. This may be a serious drawback in the case of large scale problems. Dembo and Tulowitzki [23] introduced methods for QBOPT in 1983 that are able to add and drop many constraints at each iteration. Their basic idea was further developed by Yang and Tolle [61] into an algorithm guaranteed to identify the face containing a local solution of QBOPT in finitely many iterations, even when the solution of the problem is degenerate. For further research on QBOPT we refer the reader to [25, 26, 53, 54].

For BCOPT with a general nonlinear objective function, Bertsekas [3] proposed an active set algorithm that uses a gradient projection method to find the optimal active variables. He showed that this method is able to find the face containing a local solution very quickly. Further research on convergence and properties of projected gradient methods can be found in [3, 14, 28]. The idea of using gradient projections for identifying optimal active constraints was followed up by many researchers. Most of them [12, 15, 16] combined Newton type methods with the gradient projection method to speed up the convergence. For example, LBFGSB, developed by Byrd et al. [12], performs the gradient projection method by computing the Cauchy point to determine the active variables. After determining the set of active variables, the algorithm performs line searches along the search directions obtained by a limited memory BFGS method [13] to explore the subspace of nonactive variables. In fact, the use of limited memory BFGS matrices and the line search strategy are the main properties that distinguish this method from others, especially from the trust region type method proposed by Conn et al. [15, 16].

A non-monotone line search was first introduced by Grippo et al. (GLL) in [36] for Newton methods, to improve the ability to follow a curved valley with steep walls. Later several works [19, 22, 29, 37, 59, 62] on non-monotone line search methods pointed out that these methods are more efficient than monotone line search methods in many cases. Other papers [4, 8, 20, 21, 32, 50, 58] indicate that gradient projection approaches based on a Barzilai–Borwein step size [2] have impressive performance in a wide range of applications. Recent works [5, 6, 8,9,10, 57] on Barzilai–Borwein gradient projection methods (BBGP) have modified them by incorporating them with the GLL non-monotone line search: For instance, Raydan [57] developed the BBGP method for solving unconstrained optimization problems, and Dai and Fletcher [20, 21] proposed BBGP methods for large-scale bound constrained quadratic programming. The idea of Raydan [57] was further developed to generate a convex constrained solver (SPG) by Birgin et al. [8, 9] and a bound constrained solver (GENCAN) by Birgin et al. [5, 6], enriched by an active set strategy.

The GALAHAD package [34] uses as bound-constrained solver LANCELOT-B, a trust-region algorithm using truncated Newton directions. Recently, Burdakov et al. [11] constructed a family of limited memory quasi Newton methods for unconstrained optimization combined with line searches or trust regions, called the LMBFG package.

To deal with negative curvature regions, Birgin and Martínez [5] used the second-order trust region algorithm of Zhang and Xu [63], and Birgin and Martínez [6] designed a new algorithm whose line search iteration is performed by means of backtracking and extrapolation. Hager and Zhang [43] developed an active set algorithm called $\texttt {ASACG}$ for large scale bound constrained problems. $\texttt {ASACG}$ consists of two main steps within a framework for branching between these two steps: a non-monotone gradient projection step, called NGPA, which is based on their research on the cyclic Barzilai–Borwein method [22], and an unconstrained step that utilizes their developed conjugate gradient algorithms [40,41,42, 44]. ASACG version 3.0 was updated by calling CGdescent version 6.0 which uses the variable HardConstraint to evaluate the function or gradient at a point that violates the bound constraints, so it could improve performance by giving the code additional flexibility in the starting step size routine. In 2017, Cristofari et al. [18] proposed a two-stage active set algorithm for bound-constrained optimization, called ASABCP. ASABCP first finds an active set estimation with a guarantee that the function value is reduced. Then it uses a truncated-Newton technique in the subspace of non-active variables.

A considerable amount of literature has been published on line search algorithms, which enforce the Wolfe conditions (Wolfe [60]) or the Goldstein conditions (Goldstein [33]). One problem with line search algorithms satisfying the Wolfe conditions is the need to calculate a gradient at each trial point. On the other hand, line search algorithms based on the Goldstein conditions are gradient-free, but they have very poor behaviour in severely nonconvex regions. Neumaier and Azmi [55] introduced a new active set method BOPT (Algorithm 9.1 in [55] = Algorithm 1) using an efficient gradient-free curved line search CLS (Algorithm 3.3 in [55] = Algorithm 2). The active set strategy used in BOPT always enforces that the gradient reduction in the components restricted by non-active variables over the reduced gradient reduction is at least asymptotically bounded. This property of the active set can remove zigzagging, a possible source of inefficiency. On the other hand, CLS has good properties in theory and achieves a reasonable reduction of the objective function.

This paper introduces an efficient version of BOPT, called LMBOPT, for bound constrained optimization problems with a continuously differentiable objective function. LMBOPT preserves the main structure of BOPT – the active set strategy and CLS. To get rid of getting stuck in nearly flat regions, LMBOPT uses safeguards in finite precision arithmetic, resulting in an improved version of CLS and a regularized conjugate gradient direction. In addition, many other practical enhancements are used, including a new limited memory method. A solver choice is based on our findings from an extensive numerical results. It depends on the problem dimension, the presence or absence of constraints, the desired robustness, and the relative costs of the function and gradient evaluations.

1.2 BOPT: an active set method for bound constrained optimization

Recently, Neumaier and Azmi [55] gave a comprehensive convergence theory for a generic algorithm for the bound constrained optimization problem (1) with a continuously differentiable objective function, called BOPT. The reduced gradient $g^{\text{ red }}(x)$ at a point x, whose components are

$$\begin{aligned} g^{\text{ red }}(x)_i{:}{=} {\left\{ \begin{array}{ll} 0 &{} \text { if }x_i =\underline{x}_i =\overline{x}_i , \\ \text { min}(0,g_i) &{} \text { if } x_i = \underline{x}_i <\overline{x}_i , \\ \text { max}(0,g_i) &{} \text { if } x_i = \overline{x}_i >\underline{x}_i , \\ g_i &{} \text { otherwise}, \end{array}\right. } \end{aligned}$$

(2)

(where $g_i{:}{=}g_i(x)$ is the ith component of gradient vector at x) vanishes at a local minimizer. At each point x during the iteration, a search direction is determined in a subspace obtained by varying the part indexed by a working set I, chosen either as the minimal set

$$\begin{aligned} I_-(x){:}{=}\{i\mid \underline{x}_i<x_i<\overline{x}_i\} \end{aligned}$$

(3)

of free indices or as the maximal set

$$\begin{aligned} \begin{array}{lll} I_+(x)&{}{:}{=}&{}I_-(x)\cup \left\{ i\mid g^{\text{ red }}_i\ne 0\right\} \\ &{}=&{}I_-(x)\cup \left\{ i\mid \underline{x}_i=x_i<\overline{x}_i, g_i<0 \text{ or } \underline{x}_i<x_i=\overline{x}_i, g_i>0 \right\} \end{array} \end{aligned}$$

(4)

of free or freeable indices. To ensure the absence of severe zigzagging, freeing iterations in which

$$\begin{aligned} I=I_+(x)\ne I_-(x), \end{aligned}$$

(5)

are restricted to cases where the choice $I=I_-(x)$ violates the inequality

$$\begin{aligned} \Vert g_I\Vert ^2_*\ge \rho \Vert g^{\text{ red }}\Vert ^2_*, \ \ \text{ for } \text{ some } \rho \in ]0,1]\text{. } \end{aligned}$$

(6)

Here $\Vert \cdot \Vert _*$ is the dual norm of a monotone norm $\Vert \cdot \Vert$, defined by $\Vert g\Vert _*{:}{=}\displaystyle \sup _{p\ne 0}g^Tp/\Vert p\Vert$, and $g_I$ stands for the restriction of g to the index set I. More generally, we denote by $x_I$ the subvector of a vector x with indices taken from the set I, by $A_{:k}$ the kth column of a matrix A, and by $A_{II}$ the submatrix of A with row and column indices taken from I.

BOPT takes a starting point $x^0\in {\mathbb {R}}^n$ and the feasible set $\mathbf{x}$ as input and returns an optimal point $x^{{\text{ best }}}$ and its function value $f^{{\text{ best }}}=f(x^{{\text{ best }}})$ as output. It uses the tuning parameters of a line search CLS (discussed in Sect. 1.3) and two tuning parameters:

$0<\varDelta _{\mathop {\mathrm {a}}}<1$ (parameter for the angle condition),

$0<\rho \le 1$ (parameter for freeing iterations).

The bent line search and conditions (6)–(9) on the search direction are essential for the convergence analysis in [55, Sects. 8 and 11], where the following is proved:

Theorem 1

Let f be continuously differentiable, with Lipschitz continuous gradient g. Let $x^\ell$ denote the value of x in Algorithm 1 after its $\ell$th update. Then one of the following three cases holds:

(i) The iteration stops after finitely many steps at a stationary point.

(ii) We have

$$\begin{aligned} \lim _{\ell \rightarrow \infty } f(x^\ell )= \widehat{f} \in {\mathbb {R}},~~~ \inf _{\ell \ge 0}\, \Vert g^{\text{ red }}(x^{\ell })\Vert _*=0. \end{aligned}$$

Some limit point $\widehat{x}$ of the $x^\ell$ satisfies $f(\widehat{x})=\widehat{f} \le f(x^0)$ and $g^{\text{ red }}(\widehat{x})=0$.

(iii) $\displaystyle \sup _{\ell \ge 0}\, \Vert x^{\ell }\Vert =\infty$.

Moreover, if BOPT converges to a nondegenerate stationary point, all strongly active variables are ultimately fixed, so that zigzagging through changes of the active set cannot occur infinitely often.

1.3 CLS: the curved line search of BOPT

CLS (Algorithm 3.3 in [55] = Algorithm 2 below), the line search used in BOPT, is an efficient gradient-free curved line search algorithm. It searches a piecewise linear path defined by directions chosen to reduce zigzagging. It takes the $\ell$th point $x^\ell$ and its function value $f^\ell = f(x^\ell )$, the gradient vector $g^\ell = g(x^\ell )$, the search direction $p^\ell$, the feasible set $\mathbf{x}$, and the initial step size $\alpha ^{{\text{ init }}}$ as input and returns the $(\ell +1)$th point $x^{\ell +1}=x(\alpha ^\ell )$, its step size $\alpha ^\ell$, and its function value $f^{\ell +1}=f(x^{\ell +1})$ as output. It uses several tuning parameters:

$\beta \in {]0,\frac{1}{4}[}$ (parameter for efficiency),

$q>1$ (extrapolation factor),

the positive integer $l^{\max }$ (limit on the number of iterations),

$\alpha ^{\max }$ (maximal value for the step size $\alpha$).

• Condition (13) is an improved form of the Goldstein condition

  $$\begin{aligned} 0<\mu ''\le \mu (\alpha )\le \mu '<1. \end{aligned}$$

  It forbids step sizes too large or too small by enforcing that $\mu (\alpha )$ is sufficiently positive and not too close to one.

• According to Theorem 3.2 of [55], a step size satisfying (13) can be found by performing CLS if the objective function f is bounded below.

• If the objective function is quadratic and an exact line search reveals that the secant step size is a minimizer of a convex quadratic function along the search ray and so the quadratic case is optimally started. Otherwise the function is far from quadratic and bounded.

1.4 LMBOPT: an efficient version of BOPT

In this paper we introduce a new limited memory method for bound-constrained optimization called LMBOPT. It conforms to the assumptions of BOPT, hence converges to a stationary point in exact arithmetic and fixes all strongly active variables after finitely many iterations, but also takes care of various efficiency issues that are difficult to explain in theory but must be addressed in a robust and efficient implementation.

Important novelties compared to the literature are

• the useful trick of moving the starting point slightly into the relative interior of the feasible domain $\mathbf{x}$,

• a useful starting direction based on the gradient signs,

• a new quadratic limited memory model for progressing in a subspace,

• a numerically stable version of the descent direction proposed by Neumaier and Azmi [55] for removing zigzagging,

• a new regularized conjugate gradient direction,

• safeguards for the curved line search taking into account effects due to finite precision arithmetic,

• new heuristic methods for an initial step size, for a robust minimal step size, and for handling null steps without progress in the line search, Taken together, these enhancements make LMBOPT very efficient and robust. We describe how to compute search directions in Sect. 2:

• Subspace information is defined in Sect. 2.1.

• A new quasi Newton direction and a regularized conjugate gradient step are introduced in Sects. 2.2 and 2.3, respectively.

• Some implementation details of these directions are given in Sect. 2.4.

Improvements in the line search are discussed in Sect. 3:

• Issues with finite arithmetic are described in Sect. 3.1.

• Ingredients of an improved version of CLS are introduced in Sect. 3.

We introduce the master algorithm and its implementation details in Sect. 4:

• A useful starting point is suggested in Sect. 4.1.

• The conditions for accepting a new point are explained in Sect. 4.2.

• Some implementation details are given in Sect. 4.3.

• The master algorithm is introduced in Sect. 4.4.

Numerical results for unconstrained and bound constrained CUTEst problems [35] are summarized in Sect. 5:

• Details of test problems and a shifted starting point are discussed in Sect. 5.1.

• Default parameters for LMBOPT are given in Sect. 5.2.

• Section 5.3 contains a list of all compared solvers and explains how unconstrained solvers turn into bound constrained solvers.

• First numerical results are given in Sect. 5.4.1, resulting in the three best solvers (LMBOPT, ASACG, and LMBFG-EIG-MS).

• Additional numerical results classified by constraints and dimensions are given in Sect. 5.4.2, resulting in a solver choice in Sect. 5.6.

• Further numerical results for hard problems are given in Sect. 5.5.

• As a consequence, a solver choice is based on our findings depending on the problem dimension, the presence or absence of constraints, the desired robustness, and the relative costs of the function and gradient evaluations in Sect. 5.6.

Kimiaei [47] contains public Matlab source code for LMBOPT together with more detailed documentation and an extensive list of tables and figures with numerical results and comparisons.

2 Search directions

In this section, we describe the search direction used at each iteration. In Sect. 2.1, subspace information is described. Accordingly, a new limited memory quasi Newton direction is discussed in Sect. 2.2. Then Sect. 2.3 describes how conjugate gradient directions are constructed and regularized. Finally, Sect. 2.4 contains the implementation details of our regularized conjugate gradient direction.

2.1 Subspace information

After each iteration we form the differences

$$\begin{aligned} s=x-x^{{{\text{ old }}}},~~~y=g-g^{{{\text{ old }}}}, \end{aligned}$$

where x, g are the current point and gradient, and $x^{{{\text{ old }}}},g^{{{\text{ old }}}}$ are the previous point and gradient.

For some subspace dimension m, the matrix $S\in {\mathbb {R}}^{n \times m}$ has as columns (in the actual implementation a permutation of) m previous point differences s. A second matrix $Y\in {\mathbb {R}}^{n \times m}$ has as columns the corresponding gradient differences y.

If the objective function is quadratic with (symmetric) Hessian B and no rounding errors are made, the matrices $S, Y\in {\mathbb {R}}^{n\times m}$ satisfy the quasi-Newton condition

$$\begin{aligned} BS=Y. \end{aligned}$$

(7)

Since B is symmetric,

$$\begin{aligned} H{:}{=}S^TY=S^TBS \end{aligned}$$

(8)

must be symmetric. If we calculate $y=Bs$ at the direction $s\ne 0$, we have the consistency relations

$$\begin{aligned} h{:}{=}S^TB s=Y^Ts=S^Ty, \end{aligned}$$

(9)

$$\begin{aligned} 0<\gamma {:}{=}s^TB s=y^Ts, \end{aligned}$$

(10)

for all $\alpha \in {\mathbb {R}}$ in exact precision arithmetic. If the columns of S (and hence those of Y) are linearly independent then $m\le n$, and H is positive definite. Then the minimum of $f(x+Sz)$ with respect to $z \in {\mathbb {R}}^m$ is attained at

$$\begin{aligned} z^{\text{ new }}{:}{=}-H^{-1}c \ \ \hbox { with}\ c{:}{=}S^Tg, \end{aligned}$$

(11)

where the associated point and gradient are

$$\begin{aligned} x^{\text{ new }}{:}{=}x+S z^{\text{ new }},~~~g^{\text{ new }}{:}{=}g\big (x^{\text{ new }}\big )=g+Y z^{\text{ new }}, \end{aligned}$$

and we have

$$\begin{aligned} S^Tg\big (x^{\text{ new }}\big )=0. \end{aligned}$$

(12)

If m reaches its limits, we use $\gamma {:}{=}y^Ts$ and form the augmented matrices

$$\begin{aligned}&S^{\text{ new }}{:}{=}\begin{pmatrix}S~~s\end{pmatrix},~~~Y^{\text{ new }}{:}{=}BS^{\text{ new }}{:}{=}\begin{pmatrix}Y~~y\end{pmatrix},\nonumber \\&\quad H^{\text{ new }}{:}{=}\big (S^{\text{ new }}\big )^T BS^{\text{ new }}{:}{=}\begin{pmatrix}H &{} h \\ h^T &{} \gamma \end{pmatrix}, \end{aligned}$$

(13)

the augmented vector $c^{\text{ new }}{:}{=}(S^{\text{ new }})^T g^{\text{ new }}=\begin{pmatrix}0 \\ s^Tg^{\text{ new }}\end{pmatrix}$, and put

$$\begin{aligned} z^{\text{ new }}{:}{=}-\big (H^{\text{ new }}\big )^{-1}c^{\text{ new }}. \end{aligned}$$

(14)

But when the allowed memory for S and Y is full we delete the oldest column of S and Y and the corresponding row and column of H to make room for the new pair of vectors, and then augment as described above.

The implementation contains a Boolean variable updateH as a tuning parameter to compute

$$\begin{aligned} h{:}{=}{\left\{ \begin{array}{ll} S^Ty &{} \hbox { if } \texttt { updateH}, \\ Y^Ts &{} \hbox { otherwise}. \end{array}\right. } \end{aligned}$$

(15)

If the objective is not quadratic, (7) does not hold exactly and $H{:}{=}S^TY$ need not be symmetric. However, the update (13) always produces a symmetric H, even in finite precision arithmetic.

2.2 A new quasi-Newton direction

We use S and Y to construct a Hessian approximation of the form

$$\begin{aligned} B=D+WXW^T, \end{aligned}$$

(16)

for some symmetric matrix $W\in {\mathbb {R}}^{n\times m}$ and some matrix $X\in {\mathbb {R}}^{n\times m}$. Thus, the additional assumption is temporarily made that B deviates from a diagonal matrix D by a matrix of rank at most m. Under these assumptions, we reconstruct the Hessian uniquely from the data S and $Y=BS$, in a manifestly symmetric form that can be used as a surrogate Hessian even when this structural assumption is not satisfied.

This provides an efficient alternative to the traditional L-BFGS-B formula [12], which needs twice as much storage and computation time.

Theorem 2

Let $D\in {\mathbb {R}}^{n\times n}$ be diagonal, $\varSigma \in {\mathbb {R}}^{m\times m}$ and $U\in {\mathbb {R}}^{n\times m}$. If $XW^TS$ is invertible then (7) and (16) imply

$$\begin{aligned} B=D+U\varSigma ^{-1}U^T, \end{aligned}$$

(17)

where

$$\begin{aligned} U{:}{=}Y-DS \end{aligned}$$

(18)

and

$$\begin{aligned} \varSigma {:}{=}U^TS \end{aligned}$$

(19)

is symmetric. The solution of $Bp=-g$ is given in terms of the symmetric matrix

$$\begin{aligned} M{:}=U^TD^{-1}Y=\varSigma ^{-1}, \end{aligned}$$

(20)

by the solution $p=D^{-1}(Uz-g)$ of $Mz=U^TD^{-1}g$.

Proof

The matrices $U{:}{=}Y-DS$ and $\varSigma {:}{=}U^TS$ are computable from S and Y, and we have

$$\begin{aligned} U=Y-DS=BS-DS=(B-D)S=WXW^TS, \end{aligned}$$

and since B is symmetric, $\varSigma =S^T(B-D)S$ is symmetric, too. By assumption, the $m\times m$ matrix $Z{:}{=}XW^TS$ is invertible, hence

$$\begin{aligned} W=UZ^{-1} \hbox { and } Z=XZ^{-T}U^TS =XZ^{-T}\varSigma . \end{aligned}$$

This product relation and the invertibility of Z imply that $\varSigma$ is invertible, too, and we conclude that $X=Z\varSigma ^{-1}Z^T$, hence

$$\begin{aligned} B=D+UZ^{-1}XZ^{-T}U^T=D+U\varSigma ^{-1}U^T. \end{aligned}$$

$\square$

To apply it to the bound constrained case, we note that the first order optimality condition predicts the point $x+p$, where the nonactive part $p_I$ of p solves the equation

$$\begin{aligned} B_{II}p_I=-g_I. \end{aligned}$$

Noting that

$$\begin{aligned} B_{II}=D_{II}+U_{I:}\varSigma ^{-1}U_{I:}^T, \end{aligned}$$

we find $D_{II}p_I+U_{I:}\varSigma ^{-1}U_{I:}^Tp_I=-g_I$, hence

$$\begin{aligned} p_I=D_{II}^{-1}(U_{I:}z-g_I), \end{aligned}$$

where $z{:}{=}-\varSigma ^{-1}U_{I:}^Tp_I$. Now $-\varSigma z=U_{I:}^Tp_I=U_{I:}^TD_{II}^{-1}(U_{I:}z-g_I)$, hence z solves the linear system

$$\begin{aligned} Mz = U_{I:}^TD_{II}^{-1}g_I. \end{aligned}$$

Here $M{:}{=}\varSigma +U_{I:}^TD_{II}^{-1}U_{I:}$ is equivalent to (20) by setting $Y=U+DS$ in (20) and using (19). With the symmetric matrix H defined by (8), we compute the symmetric $m\times m$ matrix M

$$\begin{aligned} M= & {} U^T_{I:}D^{-1}_{II}Y_{I:} =(Y_{I:}-D_{II}S_{I:})^TD^{-1}_{II}Y_{I:} = Y_{I:}^TD^{-1}_{II}Y_{I:}-S_{I:}^TY_{I:}\nonumber \\= & {} Y_{I:}^TD^{-1}_{II}Y_{I:}-H \end{aligned}$$

(21)

and find

$$\begin{aligned} z=M^{-1}U_{I:}^TD_{II}^{-1}g_I; \end{aligned}$$

(22)

hence

$$\begin{aligned} p_I=D_{II}^{-1}(U_{I:}z-g_I). \end{aligned}$$

(23)

Here, for $i=1,\cdots ,n$,

$$\begin{aligned} D_{ii}{:}{=}\sqrt{\sum _{j\in J}{} \texttt { YY}_{ij}\Big /\sum _{j\in J} \mathtt{SS}_{ij}} \end{aligned}$$

(24)

with

$$\begin{aligned} \mathtt{YY}=Y_{IJ}\circ Y_{IJ},~~~\mathtt{SS}=S_{IJ}\circ S_{IJ}, \end{aligned}$$

where J contains the indices of newest and oldest pair (s, y) and $\circ$ denotes componentwise multiplication.

Enforcing the angle condition. Due to rounding errors, a computed descent direction p need not satisfy the angle condition (8). We may add a multiple of the gradient to enforce the angle condition (8) for the modified direction

$$\begin{aligned} p^{\text{ new }}{:}{=}p-tg \end{aligned}$$

(25)

with a suitable factor $t\ge 0$; the case $t=0$ corresponds to the case where p already satisfies the bounded angle condition (8). The choice of t depends on the three numbers

$$\begin{aligned} \sigma _1{:}{=}g^Tg>0,~~~ \sigma _2{:}{=}p^Tp> 0,~~~ \sigma {:}{=}g^Tp; \end{aligned}$$

these are related by the Cauchy–Schwarz inequality

$$\begin{aligned} \sigma ^{\text{ new }}{:}{=}\frac{\sigma }{\sqrt{\sigma _1\sigma _2}}\in [-1,1]. \end{aligned}$$

We want to choose t such that the angle condition (8) holds with $p^{\text{ new }}$ in the place of p. If $\sigma ^{\text{ new }}\le -\varDelta _{\mathop {\mathrm {a}}}$, this holds for $t=0$, and we make this choice. Otherwise we may enforce the equality (8) by choosing

$$\begin{aligned} t {:}{=}\frac{\sigma +\varDelta _{\mathop {\mathrm {a}}}\sqrt{w}}{\sigma _1}\ \ \text{ with } \ \ w{:}{=}\frac{\sigma _1\sigma _2(1-(\sigma ^{{\text{ new }}})^2)}{1-\varDelta _{\mathop {\mathrm {a}}}^2}. \end{aligned}$$

(26)

The following proposition is a special case of Proposition 5.2 in [55].

Proposition 1

Suppose that $g\ne 0$ and $0<\varDelta _{\mathop {\mathrm {a}}}<1$. Then if t is chosen by (26), the search direction (27) satisfies the angle condition (8).

Given z by (22), we could compute the nonactive part of p from (23); however, this need not lead to a descent direction since B need not be positive definite. We therefore compute $u:=U_{I:}z$, and choose

$$\begin{aligned} p_I=D_{II}^{-1}(u-tg_I), \end{aligned}$$

(27)

where t is chosen analogous to (26) if this results in $t<1$, and $t=1$ otherwise. By Proposition 1, the direction (27) satisfies the angle condition (8).

2.3 A conjugate gradient step

Neumaier and Azmi [55, Sect. 7] introduced a new nonlinear conjugate gradient method chosen to reduce zigzagging for unconstrained optimization which, applied to the working subspace, may be used by BOPT to generate search directions as long as the active set does not change.

Any search direction p must satisfy $g^Tp<0$. To avoid zigzagging, [55] generated the search direction p as the vector with a fixed value $g^T p=-\overline{c}<0$ closest (with respect to the 2-norm) to the previous search direction $p^{{{{\text{ old }}}}}$. By Theorem 7.1 in [55] (applied for $B=I$),

$$\begin{aligned} p=\overline{\beta }p^{{{{\text{ old }}}}} -{\widehat{\lambda }} g, \end{aligned}$$

(28)

with

$$\begin{aligned} \overline{\beta }>0,~~~ {\widehat{\lambda }} = \frac{\overline{c}+\overline{\beta }g^Tp^{{{{\text{ old }}}}}}{g^T g}. \end{aligned}$$

(29)

The resulting method has finite termination on quadratic objective functions in exact precision arithmetic, where it reduces to linear conjugate gradients.

[55, Theorem 7.3] shows that the bounded angle condition holds for sufficiently large $\ell$ if an efficient line search such as CLS is used and there are positive constants $\kappa _1$ and $\kappa _2$ such that either $p^\ell$ is parallel to the steepest descent direction $-g^\ell$ or the conditions

$$\begin{aligned} \big (g^\ell \big )^Tg^\ell \le \kappa _1 \big (y^{\ell -1}\big )^Ty^{\ell -1}, \end{aligned}$$

(30)

$$\begin{aligned} \big (y^{\ell -1}\big )^Tp^{\ell -1} \le \kappa _2 \big (g^{\ell -1}\big )^Tp^{\ell -1} \end{aligned}$$

(31)

hold (where $y^{\ell -1}{:}{=}g^\ell -g^{\ell -1}$). Convergence is locally linear when the sequence $x^\ell$ converges to a strong local minimizer.

As in [55, Theorem 7.5] the sequence generated by (28) and (29) can be rewritten into the nonlinear conjugate gradient method of Fletcher and Reeves [30], which is equivalent to the linear conjugate gradient method of Hestenes and Stiefel [45] when f is quadratic with a positive definite Hessian matrix and bounded below. Therefore it requires at most n steps to obtain a minimizer of f in exact precision arithmetic.

As a consequence of [55, Theorem 7.3], [55, Theorem 7.6] showed that the sequence $x^\ell$ of the conjugate gradient method generated by (28) and (29) satisfies

$$\begin{aligned} \displaystyle \inf _{\ell } \Vert g^\ell \Vert _* = 0 \text{ or } \displaystyle \lim _{\ell \rightarrow \infty } f^\ell = - \infty \end{aligned}$$

and convergence is locally linear if the sequence $x^\ell$ converges to a strong local minimizer.

In this section, we discuss a new conjugate gradient method, which is equivalent to the linear conjugate gradient method of Hestenes and Stiefel [45] in the cases where f is quadratic with a positive definite Hessian matrix and bounded. Theorems 7.3, 7.5, 7.6 in [55] are valid for our conjugate gradient method in exact precision arithmetic.

The conjugate gradient method chooses the direction s in the subspace generated by typeSubspace and enforces the conjugacy relation

$$\begin{aligned} h=Y^Ts=0; \end{aligned}$$

(32)

thus making H diagonal. Both conditions together determine s up to a scaling factor: s must be a multiple of

$$\begin{aligned} p{:}{=}S r+p^{{\text{ init }}} \end{aligned}$$

(33)

for some $r\in {\mathbb {R}}^m$, in which $p^{{\text{ init }}}$ is a descent direction, computed by searchDir (discussed later in Sect. 2.4).

Then (32) requires

$$\begin{aligned} Hr=q{:}{=}-Y^Tp^{{\text{ init }}}. \end{aligned}$$

(34)

$\mathtt{hist}$ denotes the subspace basis index set (discussed later in Sect. 2.4). By restricting S, Y, and H to hist, we define

$$\begin{aligned} c_h {:}{=} \displaystyle \sum _{i\in \mathtt{hist}} g_I\circ S_{I,i}, \ \ q_h {:}{=} \displaystyle \sum _{i\in \mathtt{hist}} p^{{\text{ init }}}_I\circ Y_{I,i}, \ \ H_h {:}{=} H_{\mathtt{hist},\mathtt{hist}}. \end{aligned}$$

Then we solve the linear systems $H_h z_h{:}{=}-c_h$ and $H_h r_h{:}{=}q_h$ according to (14) and (34), respectively. Afterwards, we construct the conjugate gradient direction depending on whether the subspace is possible ($m_0>0$) or not ($m_0=0$) by

$$\begin{aligned} p_I{:}{=}{\left\{ \begin{array}{ll}-\zeta p^{{\text{ init }}}_I+S_{I,\texttt {hist}} (z_h+\zeta r_h) &{} \hbox { if } m_0>0 , \\ -\zeta p^{{\text{ init }}}_I &{} \hbox { if } m_0=0 ,\end{array}\right. } \end{aligned}$$

(35)

with

$$\begin{aligned} \zeta {:}{=}{\left\{ \begin{array}{ll}\displaystyle \frac{g^T_Ip^{{\text{ init }}}_I+q^Tz_h}{\gamma -q_h^Tr_h} &{} \hbox { if } m_0>0 ,\\ \displaystyle \frac{g^T_Ip^{{\text{ init }}}_I}{\gamma } &{} \hbox { if } m_0=0 . \end{array}\right. } \end{aligned}$$

(36)

Here $\gamma$ is computed by

$$\begin{aligned} \gamma {:}{=} \frac{f\left( x+\alpha p^{{\text{ init }}}\right) -f -\alpha g^T_Ip^{{\text{ init }}}_I}{\alpha ^2/2} \end{aligned}$$

where $\alpha$ is found by a heuristic way (goodStep; discussed later in Sect. 3).

In finite precision arithmetic, a tiny denominator in (36) produces a very inaccurate $\gamma$. This drawback is overcome by regularization. The error made in $\gamma _{{\mathop {\mathrm {reg}}}}$ is a tiny multiple of

$$\begin{aligned} \gamma _{{\mathop {\mathrm {reg}}}}{:}{=} \frac{|f\left( x+\alpha p^{{\text{ init }}}\right) -f| +\alpha |g_I|^T|p^{{\text{ init }}}_I|}{\alpha ^2/2}. \end{aligned}$$

(37)

We therefore shift the denominator in (36) away from zero to

$$\begin{aligned} \texttt { denom}{:}{=}{\left\{ \begin{array}{ll}\gamma -q_h^Tr_h+\varDelta _H\left( \gamma _{\mathop {\mathrm {reg}}}/2+|q_h|^T|r_h|\right) &{}\hbox { if } \gamma \ge q_h^Tr_h , \\ \gamma -q_h^Tr_h-\varDelta _H\left( \gamma _{\mathop {\mathrm {reg}}}/2+|q_h|^T|r_h|\right) &{} \hbox { otherwise },\end{array}\right. } \end{aligned}$$

(38)

where $\varDelta _H\in (0,1)$ is a tiny factor. Then the regularized conjugate gradient direction is computed by

$$\begin{aligned} p^{{\text{ new }}}_I{:}{=}{\left\{ \begin{array}{ll}-\zeta _{{\mathop {\mathrm {reg}}}} p^{{\text{ init }}}_I+S_{I,\texttt { hist}} (z_h+\zeta _{\mathop {\mathrm {reg}}}r_h) &{} \hbox { if } m_0>0 , \\ -\zeta _{{\mathop {\mathrm {reg}}}} p^{{\text{ init }}}_I &{}\hbox { if } m_0=0 ,\end{array}\right. } \end{aligned}$$

(39)

with

$$\begin{aligned} \zeta _{{\mathop {\mathrm {reg}}}}{:}{=}{\left\{ \begin{array}{ll}\displaystyle \frac{g^T_Ip^{{\text{ init }}}_I+q^T_hz_h}{\texttt { denom}} &{}\hbox { if } m_0>0 , \\ \displaystyle \frac{g^T_Ip^{{\text{ init }}}_I}{\gamma } &{} \hbox {if } m_0=0 .\end{array}\right. } \end{aligned}$$

(40)

If

$$\begin{aligned} \texttt { cosine} {:}{=} {\left\{ \begin{array}{ll}-\zeta _{{\mathop {\mathrm {reg}}}} g^T_Ip_I^{{\text{ init }}} + c^T_hz_h &{} \hbox {if } m_0>0 , \\ -\zeta _{{\mathop {\mathrm {reg}}}}g^T_Ip_I^{{\text{ init }}} &{}\hbox { if} m_0=0 \end{array}\right. } \end{aligned}$$

(41)

is negative, (39) is a descent direction.

2.4 Some implementation details

In this section, we first discusses how to determine the ingredients of the subspace, e.g., the subspace dimension, the subspace basis index set, the subspace type, and $p^{{\text{ init }}}$. Then we describe how to implement our regularized conjugate gradient direction.

Regardless of whether the activity changes or not, the subspace cannot be updated whenever very little progress is made, $y\approx 0$, while the gradient is still large, i.e., a new pair (s, y) violates the condition

$$\begin{aligned} |g^Ty|\ge \varDelta _{po} g^Tg, \end{aligned}$$

(42)

where $\varDelta _{po}\in (0,1)$ is a tiny tuning parameter. Initially $m=0$ and whenever a new pair (s, y) satisfies (42), m is increased by one by appending these vectors to S and Y, respectively. But once m reaches its limit, it is kept to be fixed and the oldest column of S and Y is replaced by s and y, respectively.

When the activity does not change, the step is called a local step. For the construction of our regularized conjugate gradient direction, it is important which subspace basis index set is present and what is the subspace dimension. We denote by nlocal the number of local steps and by nwait the number of local steps before starting the regularized conjugate gradient direction, which will be a tuning parameter. We use nlocal and nwait to determine the subspace dimension.

To encode which subspace should be used, typeSubspace updates three variables $m_0$ (subspace dimension), $\mathtt{hist}$ (subspace basis index set), and CG (subspace type).

Given the number of updated subspace nh, typeSubspace defines $\widehat{m} :=\min (m,\mathtt{nh})$ and identifies CG, $m_0$, and hist as follows:

• If $\mathtt{nlocal < nwait}$, the ordinary subspace step is used since the full subspace direction may be contaminated by nonactive components and so lead to premature freeing if used directly. In this case, $\mathtt{CG}{:}{=}0$, $m_0{:}{=}\min (\mathtt{ng}-1,\widehat{m})$, and $\mathtt{hist}{:}{=}\{1,\cdots ,m_0\}$.

• If $\mathtt{nlocal=nwait}$, the quasi-Newton step generated by quasiNewtonDir is used if (27) holds, and the subspace basis index set is permuted by

  $$\begin{aligned}{} \mathtt{perm}{:}{=}\{ \mathtt{ch}+1,\cdots , \widehat{m},1,\cdots ,\mathtt{ch}\} \end{aligned}$$

  so that the oldest columns are shifted with the newest, i.e.,

  $$\begin{aligned} S{:}{=}S_{:\mathtt{perm}}\text{, } Y{:}{=}Y_{:\mathtt{perm}}\text{, } \text{ and } H{:}{=}H_{\mathtt{perm},\mathtt{perm}}\text{; } \end{aligned}$$

  here $\mathtt{ch}$ is a counter for m. Then set $\mathtt{ch}{:}{=}0$. In this case, $\mathtt{CG}{:}{=}1$, $m_0{:}{=}0$, and $\mathtt{hist}{:}{=}\emptyset$. Since $m_0=0$, there is a premature replacement of s (y) by the first column of the subspace matrix S (Y) before $\mathtt{ch}$ exceeds m.

• If $\mathtt{nlocal<nwait}+\widehat{m}$, the conjugacy relation (32) is preserved by restricting the subspace. In such a case, $\mathtt{CG}{:}{=}2$, $m_0{:}{=}{} \mathtt{nlocal}-\mathtt{nwait}$, and $\mathtt{hist}{:}{=}\{1,\cdots ,m_0\}$.

• Otherwise, the full subspace step preserves the conjugacy. In this case, $\mathtt{CG}{:}{=}3$, $m_0{:}{=}\widehat{m}$, and $\mathtt{hist}{:}{=}\{1,\cdots ,\widehat{m}\}$. The value of $\gamma$ depends on the search direction. Here searchDir is used to compute $p^{{\text{ init }}}$ including scaleDir, quasiNewtonDir, and AvoidZigzagDir. It works as follows:

• In the first iteration the starting search direction makes use of the gradient signs only, and has nonzero entries in some components that can vary. Each starting search direction is computed by scaleDir. In this case, scaleDir, for $i=1,\ldots ,n$, computes

  $$\begin{aligned} \texttt { sc}{:}{=}\min (1,\overline{x}_{i}-\underline{x}_i)\ \ \text{ and }\ \ p^{{\text{ init }}}_i{:}{=}{\left\{ \begin{array}{ll}{} \texttt { sc} &{}\hbox { if}\; g_i<0 ,\\ -\texttt { sc} &{} \hbox {otherwise} \end{array}\right. } \end{aligned}$$

  if $x_i=0$; otherwise, it sets $\mathtt{sc}=|x_i|$ and computes

  $$\begin{aligned} p^{{\text{ init }}}_i{:}{=}{\left\{ \begin{array}{ll}{} \texttt { sc} &{}\hbox { if } \;x_i=\underline{x}_i ,\\ -\texttt { sc} &{} \hbox {else\,if } x_i=\overline{x}_i , \\ \texttt { sc} &{} \mathrm{{else\,if}} g_i<0 , \\ -\texttt { sc} &{} \mathrm{{otherwise}}.\end{array}\right. } \end{aligned}$$

• If $\mathtt{nlocal}\ne \mathtt{nwait}$, a modified direction is used to avoid zigzagging. $p^{{\text{ init }}}$ is computed by (28) using (29). Since $g^T_I p^{{\text{ init }}}_I = -\overline{c}$, the direction will be a descent direction. This direction is implemented by AvoidZigzagDir and enriched by a new heuristic choice of

  $$\begin{aligned} \overline{\beta }{:}{=}\theta \displaystyle \max _{i=1:n}\Big \{\Big |\frac{g_i}{p^{{\text{ init }}}_i}\Big |\Big \}, \end{aligned}$$

  (43)

  with tuning parameters $0<\theta <1$ and $\overline{c}>0$.

• Otherwise, quasiNewtonDir is used in subspace. If $D_{ii}\in [\varDelta _{D}^{-1},\varDelta _{D}]$ is violated, $D_{ii}=1$, where $\varDelta _{D}>1$ is a tuning parameter. Afterwards, enforceAngle is used if the angle condition (8) does not hold:

• If $g_I^Tp^{{\text{ init }}}_I>0$, $p^{{\text{ init }}}_I$ is chosen to be its opposite to move away from maximizer or saddle point.

• By changing the sign of g, it may enforce $g^T_Ip^{{\text{ init }}}_I\le 0$. Even though $g\ne 0$, cancellation may lead to a tiny $g^T_Ip^{{\text{ init }}}_I$ (and even with the wrong sign). Given a tiny parameter $\varDelta _{pg}$, to overcome this weakness, the subtract $\varDelta _{pg}|g_I|^T|p^{{\text{ init }}}_I|$ can be a bound on the rounding error to get the theoretically correct sign. A regularized directional derivative is done if the condition

  $$\begin{aligned} \left| g^T_Ip^{{\text{ init }}}_I\right| \le \varDelta _{pg}|g_I|^T\left| p^{{\text{ init }}}_I\right| \end{aligned}$$

  (44)

  holds, enforcing $g_I^Tp^{{\text{ init }}}_I<0$. In this case, if (44) holds, $p^{{\text{ init }}}_I$ is either $-g_I$ or $-\lambda _b g_I$. Here $\lambda _b{:}{=}\displaystyle \max _{i\in I}\{D_{ii}\}$.

• If at least one of the conditions $w>0$ and $0\le |t|<\infty$ does not hold, $p^{{\text{ init }}}_I$ is chosen to be $-\lambda _b g_I$. In summary, the implementation of our regularized conjugate gradient direction, called ConjGradDir, for computing p in (39) is given as follows: (1) $\gamma _{{\mathop {\mathrm {reg}}}}$ is computed by getGam according to (37), (2) if the subspace dimension is nonzero, our conjugate gradient direction is used; otherwise, it reduces to $p^{{\text{ new }}}=-\zeta _{{\mathop {\mathrm {reg}}}}p^{{\text{ init }}}$ and the subspace basis index set is restarted, (3) a regularization for the denominator of (40) is made according to (38) by regDenom, (4) the condition (41) is computed to know whether the regularized conjugate gradient direction is descent or not, (5) the new trial point, $x+p^{{\text{ new }}}$, is projected into $\mathbf{x}$, resulting in $x^{\text{ new }}$ and the direction is recomputed by $p^{{\text{ new }}} {:}{=} x^{\text{ new }}-x$.

3 Improvements in the line search

In this section, we introduce an improved version of CLS, called CLS-new, with enhancements for numerical stability (finding a starting step size, a target step size and a minimum step size with safeguards in finite precision arithmetic). The variable eff indicates the status of the step in CLS-new – taking the values 1 (efficient step), 2 (non-monotone step), 3 (inefficient decrease), and 4 (inefficient step).

3.1 Issues with finite precision arithmetic

Rounding errors prevent descent for step sizes that are too small.

Example 1

We consider the function

$$\begin{aligned} f(x)=x^5 - 15x^4 + 85x^3 - 225x^2 + 274x - 120. \end{aligned}$$

For $x=5+3\times 10^{-10}$ and $p=-1$, the plot $f(x+\alpha p)$ versus $\alpha$ in Fig. 1 shows that one needs to find a sensible minimal step size.

Fig. 1

In the Example 1 points with step sizes $\alpha <0.5\times 10^{-13}$ have a high probability for having $f(x+\alpha p)\ge f(x)$

In practice if the step size is too small, rounding errors will often prevent that the function value is strictly decreasing. Due to cancellation of leading digits, the Goldstein quotient can become very inaccurate, which may lead to a wrong bracket and then to failure of the line search. The danger is particularly likely when the search direction is almost orthogonal to the gradient. Hence, before each line search, we need to produce a starting step size by a method, called goodStep, to find the starting step size $\alpha ^{\mathop {\mathrm {good}}}$, the target step size $\alpha ^{{\text{ target }}}$, and the minimum step size $\alpha ^{\min }$ with safeguards in finite precision arithmetic. goodStep computes the first and second breakpoint, respectively, by

$$\begin{aligned} \underline{\alpha }^{\mathop {\mathrm {break}}}{:}{=}\min \left\{ (\underline{x}_i-x_i)/p_i\mid i\in \underline{\mathtt{ind}}\right\} , \ \ \overline{\alpha }^{\mathop {\mathrm {break}}} {:}{=} \min \left\{ (\overline{x}_i-x_i)/p_i\mid i\in \overline{\mathtt{ind}}\right\} . \end{aligned}$$

Here $\underline{\mathtt{ind}}{:}{=}\{i\mid p_i<0~ \& ~x_i>\underline{x}_i\}$ is the indices of the first breakpoint and $\overline{\mathtt{ind}} = \{i\mid p_i>0~ \& ~x_i<\overline{x}_i\}$ is the indices of the second breakpoint. Then it computes the breakpoint by $\alpha ^{\mathop {\mathrm {break}}}{:}{=}\min (\underline{\alpha }^{\mathop {\mathrm {break}}},\overline{\alpha }^{\mathop {\mathrm {break}}})$ in finite precision arithmetic and adjusts it by $\alpha ^{\mathop {\mathrm {break}}}{:}{=}\alpha ^{\mathop {\mathrm {break}}}(1+\varDelta _{b})$, where $\varDelta _{b}\in (0,1)$ is a tiny factor for adjusting a target step size. In the cases where $\underline{\mathtt{ind}}$ and $\overline{\mathtt{ind}}$ are empty, we set $\underline{\alpha }^{\mathop {\mathrm {break}}}{:}{=}+\infty$ and $\overline{\alpha }^{\mathop {\mathrm {break}}}{:}{=}+\infty$. Given a tiny factor $\varDelta _{\alpha }\in (0,1)$ and an index set $\mathtt{indp}{:}{=}\{i\mid p_i\ne 0\}$, the minimal step size is computed by a heuristic formula

$$\begin{aligned} \alpha ^{\min }{:}{=}{\left\{ \begin{array}{ll}\min \Big (1,\varDelta _{\alpha }\Big |\displaystyle \frac{f}{g^Tp}\Big |\Big ) &{} \hbox {if}\; x=0 \; \hbox {and} \; \texttt { indp}\ne \emptyset ,\\ \min \Big (1,\varDelta _{\alpha }\displaystyle \min \Big (\Big |\displaystyle \frac{f}{g^Tp}\Big |,\min _{i\in \texttt { ind}}\Big \{\Big |\frac{x_i}{p_i}\Big |\Big \}\Big )\Big )&{} \hbox {elseif} \texttt { indp}\ne \emptyset ,\\ 1&{} \hbox {otherwise},\end{array}\right. } \end{aligned}$$

and the target step size is chosen by $\alpha ^{{\text{ target }}}{:}{=}\max (\alpha ^{\min },\mathtt{df}/|g^Tp|)$. We discuss how df is computed in the next subsection. If an exact line search on quadratic is requested, $\alpha ^{{\text{ target }}}$ is restricted by

$$\begin{aligned} \alpha ^{{\text{ target }}}:=\min \left( \alpha ^{{\text{ target }}},\alpha ^{\mathop {\mathrm {break}}}\right) . \end{aligned}$$

In the special case, if $\alpha ^{\min }=1$, $\alpha ^{\mathop {\mathrm {good}}}{:}{=}1$ and goodStep ends due to being the zeros direction; otherwise, it computes the good step size by

$$\begin{aligned} \alpha ^{\mathop {\mathrm {good}}}{:}{=}{\left\{ \begin{array}{ll} \alpha ^{{\text{ target }}}&{}\hbox { if}\; q\;\alpha ^{{\text{ target }}}\le \alpha ^{\mathop {\mathrm {break}}},\\ \max \left( \alpha ^{\min },\alpha ^{\mathop {\mathrm {break}}}\right) &{} \hbox {otherwise};\end{array}\right. } \end{aligned}$$

when it equals $\alpha ^{\min }$, adverse finite precision effects are avoided. Here $q>1$ is an input parameter for goodStep which is used to expand (reduce) step sizes by CLS-new.

The number of stuck iterations is the number nstuck of times that LMBOPT cannot update the best point. Its limits are nstuckmax (maximum number of all stuck iterations) and nsmin (how many stucks are allowed before a trial point is accepted), both of which will be tuning parameters. In the final step of goodStep, if $\mathtt{nstuck} \ge \mathtt{nsmin}$, $\alpha ^{\mathop {\mathrm {good}}}$ is increased by the factor $2*\mathtt{nstuck}$ to avoid remaining stuck.

3.2 CLS-new: an improved version of CLS

Before CLS-new tries to enforce the sufficient descent condition (13), the following steps are taken:

• LMBOPT calls enforceAngle to enforce the angle condition (8).

• Once LMBOPT calls initInfo to initialize the best function value $f^{{\text{ best }}}{:}{=}f^0$ and to compute the factor for adjusting increases in f (discussed below)

  $$\begin{aligned} \delta _f{:}{=}{\left\{ \begin{array}{ll} \texttt { facf}*|f^0| &{}\hbox { if} f^0 \in (0,\infty ), \\ 1 &{} \hbox {otherwise}, \end{array}\right. } \end{aligned}$$

  (45)

  where $\mathtt{facf}>0$ is a relative accuracy of $f^0$. We denote the list of acceptable increases in f by Df and its size by $\mathtt{mf}$ and the number of gradient evaluations by ng. Moreover, initInfo chooses, for $i=1,\cdots ,\mathtt{mf}-1$, $\mathtt{Df}_i{:}{=}-\infty$ and $\mathtt{Df}_{\mathtt{mf}}{:}{=}\delta _f$. After the first call to CLS-new, LMBOPT always calls updateInfo to update

  • (1) the number of times that the best point is not updated by

    $$\begin{aligned}{} \mathtt{nstuck}{:}{=}{\left\{ \begin{array}{ll}0 &{} \hbox {if }f^{{\text{ new }}}<f^{{\text{ best }}},\\ \texttt { nstuck}+1 &{} \hbox {otherwise};\end{array}\right. } \end{aligned}$$

  • (2) the best point information by $f^{{\text{ best }}}{:}{=}f^{{\text{ new }}}$ and $x^{\text{ best }}{:}{=}x^{\text{ new }}$ if $\mathtt{nstuck}=0$;

  • (3) $\delta _f$ and Df. In this case, if $f^{{\text{ new }}}<f$, then $\delta _f{:}{=}f-f^{{\text{ new }}}$ and $\mathtt{nm} {:}{=} \mathop {\mathrm {mod}}(\mathtt{ng}, \mathtt{mf})$ are computed. Otherwise since the function value is not decreased, $\delta _f$ is expanded by $\delta _f{:}{=}\max (\varDelta _f\delta _f,\varDelta _m(|f|+|f^{{\text{ new }}}|))$ and $\mathtt{nm} {:}{=} \mathop {\mathrm {mod}}(\mathtt{ng}, \mathtt{mf})$ is updated. Here $\varDelta _m\in (0,1)$ is a tiny factor for adjusting $\delta _f$ and $\varDelta _f>1$ is a tuning parameter for expanding $\delta _f$. If $\mathtt{nm}$ is zero, the last component of $\mathtt{Df}$ is replaced by $\delta _f$; otherwise, the nmth component of $\mathtt{Df}$ is replaced by $\delta _f$;

  • (4) f by $f^{{\text{ new }}}$ if $f^{{\text{ new }}}<f$ holds.

• If $\alpha ^{\mathop {\mathrm {good}}}\ge 1$, q is updated by $q=\max \Big (q^{\min },q/\varDelta _q\Big )$, where $1<q^{\min }<q$ and $0<\varDelta _q<1$ are the tuning parameters. Whenever the term $q \alpha ^{\mathop {\mathrm {good}}}$ is moderately large, this choice may helps CLS-new to prevent a failure. To get target step sizes which should not become too small, an acceptable increase in f (denoted by df) must be estimated in a heuristic way such that it becomes slowly small. Accordingly, at first, df is $\delta _f$ computed by (45). Next, it is a multiple of the old $\delta _f$ value if the tuning parameter mdf divides ng. Otherwise it is the maximum of the mf old $\delta _f$ valuesİn this case, target step sizes do not become too small.

• goodStep is used to find an initial step size. CLS-new tries to find a step size $\alpha >0$ satisfying the sufficient descent condition (13).

• CLS-new ends once the sufficient descent condition holds, resulting in the line search being efficient and $\mathtt{eff}=1$.

• In the first iteration if the Goldstein quotient satisfies $\mu (\alpha )<1$ an exact line search uses the secant step $\frac{1}{2}\alpha /(1-\mu (\alpha ))$ for the quadratic objective function. In fact this ensures finite termination of our conjugate gradient method for the quadratic functions. Otherwise extrapolation is done by the factor $q>1$. In the next iteration, if the sufficient descent condition (13) does not hold, then the function is far from quadratic and bounded. In such a case, either interpolate is performed if the lower bound on the step size is zero or extrapolation is done by the factor $q>1$ until a bracket $[\underline{\alpha },\overline{\alpha }]$ is found. Then, a geometric mean of $\underline{\alpha }$ and $\overline{\alpha }$ is used.

• A limit on the number of iterations is used.

• If CLS-new ends up providing no improvement in the function values, LMBOPT calls robustStep to find a step size with corresponding lowest function value. Such a step size is called robust. Using a list of differences between the current best function value and the function values at trial points as gains, robustStep tries to find a point with smallest robust change if the minimum of gains is smaller than or equal to the acceptable increase in f ($\mathtt{df}$). Otherwise, if the function is almost flat or flat a step with largest gain is chosen. Otherwise, a point with nonrobust change might be chosen provided that the minimum of gains $\le \varDelta _r\mathtt{df}$, where $\varDelta _r>0$ is a tuning parameter.

After LMBOPT accepts a new point $x^{{\text{ new }}}$ and its step size $\alpha$ by CLS-new, the new step is defined by $s{:}{=}x^{{\text{ new }}}-x = \alpha \Vert p\Vert$. Due to the inefficiency of CLS-new, $\alpha$ may be too small, so that $\Vert s\Vert$ goes to zeros. s with zero size is called a null step. If there have been too many null steps, LMBOPT cannot update the subspace information too many iterations, resulting a failure. To get rid of this weakness, nullStep is used, depending on whether CLS-new is inefficient or not. If CLS-new is inefficient ($\mathtt{eff}=4$), the new point $x^{{\text{ new }}}$ is a multiple of the current best point. Otherwise, it is a multiple of the current point generated by CLS-new. Given a tiny tuning parameter del, $x^{{\text{ new }}}$ is adjusted by a factor of $1-\mathtt{del}$ and all its zero components (if any) are replaced by del in both cases. Then it is projected into the feasible set $\mathbf{x}$.

4 Starting point and master algorithm

4.1 projStartPoint: the starting point

A poor choice of the starting point can lead to inefficiencies. For example, consider minimizing the quadratic function

$$\begin{aligned} f(x){:}{=}(x_1-1)^2+\displaystyle \sum _{i=2}^n (x_i-x_{i-1})^2 \end{aligned}$$

that starts with $x^0=0$. If a diagonal preconditioner is used, it is easy to see by induction that, for any method that chooses its search directions as linear combinations of the preconditioned gradients computed earlier, the ith iteration point has zero in all coordinates $k>i$ and its gradient has zero in all coordinates $k>i+1$. Since the solution is the all-one vector, this implies that at least n iterations are needed to reduce the maximal error in the components of x to below one.

Situations like this are likely to occur when both the Hessian and the starting point are sparse. To avoid this, projStartPoint moves a user-given starting point x slightly into the relative interior of the feasible domain.

4.2 getSuccess: successful iteration

The goal of getSuccess is to test whether the sufficient descent condition (13) holds or not; the only difference being that the tuning parameter $\beta$ is replaced by the other tuning parameter $\beta ^{\mathtt{CG}}$. The Goldstein quotient (12) is computed provided that all of the following hold:

• The regularized conjugate gradient direction is descent, i.e., (41) is negative, but it is not zero.

• $\mathtt{nlocal}\ge \mathtt{nwait}$ or $\mathtt{nstuck} \ge \mathtt{nsmin}$.

After computing the Goldstein quotient (12), the iteration will be successful if either line search is efficient, meaning the sufficient descent condition (13) with $\beta =\beta ^{\mathtt{CG}}$ holds, or there exists an improvement in the function value by at least $\delta _f$ and $\mathtt{nstuck}\ge \mathtt{nsmin}$. In this case, the Boolean variable $\mathtt{success}$ is evaluated as true; otherwise, it is evaluated as false.

4.3 Some implementation details

To determine the working set I, it is checked if one of the following holds:

• (1) The function value cannot be decreased.

• (2) The size of the new free index set is smaller than that of the old free index set (i.e., the activity is not fixed).

• (3) The maximal number of local steps before finding the freeing iteration (which is a tuning parameter) is exceeded.

• (4) Condition (6) is violated.

We use the algorithms findFreePos and findFreeNeg to get the working set. At the first iteration, BOPT calls findFreePos to find $I_+(x)$ by (4) and initializes the working set with $I(x){:}{=}I_+(x)$. Then if the statements (1)-(3) are true, findFreeNeg finds $I_-(x)$ by (3) and findFreePos checks whether the statement (4) is true or not. If this statement is not true, the working set is $I(x){:}{=}I_-(x)$; otherwise, findFreePos finds $I_+(x)$ by (4) and chooses it as the new working set $I(x){:}{=}I_+(x)$.

If at least one of the statements (1)–(4) holds, a scaled Cauchy point is tried. It is computed in the same way as [46] but with the difference that the scaling matrix is computed by

$$\begin{aligned} \overline{D}_{ii}{:}{=}\sqrt{\sum _{j=1}^{m}{} \mathtt{YY}_{ij}\Big /\sum _{j=1}^{m} \mathtt{SS}_{ij}}, \ \ \hbox { for}\ i=1,\ldots ,n \end{aligned}$$

with

$$\begin{aligned} \mathtt{YY}=Y\circ Y,~~~\mathtt{SS}=S\circ S, \end{aligned}$$

where $\circ$ denotes componentwise multiplication, if at least once S and Y are updated. Otherwise, it is computed by

$$\begin{aligned} \overline{D}_{ii}{:}{=}\Big |\frac{g_i}{p^{{\text{ init }}}_i}\Big |, \ \ \text{ for } i=1,\ldots ,n\text{, } \end{aligned}$$

where $p^{{\text{ init }}}$ is computed as discussed above.

4.4 The master algorithm

We now recall the main ingredients of LMBOPT, the new limited memory bound constrained optimization method. The mathematical structure of LMBOPT is described in Sect. 1 of suppMat.pdf. LMBOPT first calls projStartPoint described in Sect. 4.1 to improve the starting point. Then the function value and gradient vector for such a point are computed and adjusted by adjustGrad; the same computation happens later for other points. In practice, if the gradient is contaminated by NaN or $\pm \infty$, adjustGrad replaces these values by a tuning parameter. In the main loop,

• LMBOPT first computes the reduced gradient by redGrad in each iteration and then the working set is determined and updated by findFreePos.

• As long as the reduced gradient is not below a minimum threshold, it generates the direction $p^{{\text{ init }}}$ by searchDir to construct the subspace, and then constructs the regularized conjugate gradient direction p by ConjGradDir to achieve a successful iteration, provided the activity is changed; otherwise the scaled Cauchy point is computed by scaleCauchy if at least one of the statements (1)–(4) holds, discussed earlier in Sect. 2.4. Such a successful iteration is determined by getSuccess and then the best point is updated.

• Otherwise it performs a gradient-free line search CLS-new along a regularized direction (enforceAngle) since the function is not near the quadratic case.

• Then if at least nnullmax null steps are repeated in a sequence, the point leading to such steps is replaced by nullStep with a point around the previous best point if CLS-new is not efficient; otherwise by the current point generated by CLS-new. This is repeated until no null step is found.

• Afterwards, the gradient at the new point is computed and adjusted by adjustGrad. In addition, the new free index set is found by findFreeNeg. At the end of every iteration, the subspace is updated provided that (1) there is no more null step, (2) either the condition (42) holds or the number of local steps exceeds its limit. LMBOPT minimizes the bound constrained optimization problem (1). It takes the initial point $x^0$, the feasible set $\mathbf{x}$ and the tuning parameters—detailed in Table 4 in suppMat.pdf—as input and returns an optimum point $x^{{\text{ best }}}$ and its function value $f^{{\text{ best }}}$ as output. For the convergence analysis of Algorithm 3 we refer to Theorem 1.

LMBOPT was implemented in Matlab; the source code is obtainable from

https://www.mat.univie.ac.at/~neum/software/LMBOPT or https://doi.org/10.5281/zenodo.5607521.

5 Numerical results

In this section we compare our new solver LMBOPT with many other state-of-the-art solvers from the literature (see Sect. 5.3) on a large public benchmark. Only summary results are given; supplementary information with much more detailed test results can be found in suppMat.pdf from the LMBOPT web site.

5.1 Test problems used

As test problems we used all 1088 unconstrained and bound constrained problems with up to 100001 variables from the CUTEst collection of optimization problems by Gould et al. [35], in case of variable dimension problems for all allowed dimensions in this range; see Sect. 5 of suppMat.pdf.

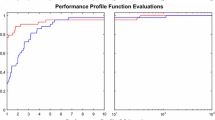
nf, ng, and sec denote the number of function evaluations, the number of gradient evaluations, and the time in seconds, respectively. Since the cost of computing the gradient is typically about twice the cost of the function value (see Sect. 3 of suppMat.pdf), we also use the cost measure $\mathtt{nf2g} {:}{=} \mathtt{nf+2ng}$. These measures are used as the cost measures to do performance profiles [24] and box plots shown in Figs. 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18 and 19.

Fig. 2

For unconstrained problems ($1\le n\le 100001$). $\rho$ designates the percentage of problems solved within a factor $\tau$ of the best solver. Problem solved by no solver are ignored

Fig. 3

For bound constrained problems ($1\le n\le 100001$). Other details as in Fig. 2

Fig. 4

For both unconstrained and bound constrained problems ($1\le n\le 100001$). Other details as in Fig. 2

Fig. 5

For low-dimensional unconstrained problems ($1\le n\le 30$). Other details as in Fig. 2

Fig. 6

For low-dimensional bound constrained problems ($1\le n\le 30$). Other details as in Fig. 2

Fig. 7

For medium-dimensional unconstrained problems ($31\le n\le 500$). Other details as in Fig. 2

Fig. 8

For medium-dimensional bound constrained problems ($31\le n\le 500$). Other details as in Fig. 2

Fig. 9

For high-dimensional unconstrained problems ($501\le n\le 100001$). Other details as in Fig. 2

Fig. 10

For high-dimensional bound constrained problems ($501\le n\le 100001$). Other details as in Fig. 2

Fig. 11

For low-dimensional unconstrained problems ($1\le n\le 30$). $\rho$ designates the percentage of problems solved and s denotes the name of solvers compared. Problem solved by no solver are ignored

Fig. 12

For low-dimensional bound constrained problems ($1\le n\le 30$). Other details as in Fig. 11

Fig. 13

For medium-dimensional unconstrained problems ($31\le n\le 500$). Other details as in Fig. 11

Fig. 14

For medium-dimensional bound constrained problems ($31\le n\le 500$). Other details as in Fig. 11

Fig. 15

For high-dimensional unconstrained problems ($501\le n\le 100001$). Other details as in Fig. 11

Fig. 16

For high-dimensional bound constrained problems ($501\le n\le 100001$). Other details as in Fig. 11

Fig. 17

For unconstrained hard problems ($1\le n\le 100001$). Other details as in Fig. 2

Fig. 18

For bound constrained hard problems ($1\le n\le 100001$). Other details as in Fig. 2

Fig. 19

For both unconstrained and bound constrained hard problems ($1\le n\le 100001$). Other details as in Fig. 2

We limited the budget available for each solver by requiring

$$\begin{aligned} \mathtt{nf2g} \le {\left\{ \begin{array}{ll}20n+10000 &{} \hbox {in the first and second runs,} \\ 50n+200000 &{} \hbox {in the third run}\end{array}\right. } \end{aligned}$$

function evaluations plus two times gradient evaluations for a problem with n variables and allowing at most

$$\begin{aligned} {\left\{ \begin{array}{ll}300 &{} \hbox {in the first run}, \\ 1800 &{} \hbox {in the second run},\\ 7200 &{} \hbox {in the third run}\end{array}\right. } \end{aligned}$$

sec of run time. A problem is considered solved if $\Vert g^k\Vert \le 10^{-6}$.

To identify the best solver under appropriate conditions on test problems and budgets, we made three different runs:

• In the first and second runs, the initial point is $x^0{:}{=}0$, but we shift the arguments by

  $$\begin{aligned} \xi _i {:}{=} (-1)^{i-1}\frac{2}{2+i}, \ \ \hbox { for all}\ i=1,\ldots ,n \end{aligned}$$

  (46)

  to avoid a solver guessing the solution of toy problems with a simple solution (such as all zero or all one) – there are quite a few of these in the CUTEst library. This means that the initial point is chosen by $x^0{:}{=}\xi$ and the initial function value is $f^0{:}{=}f(x^0)$ while the other function values are computed by $f^\ell {:}{=}f(x^{\ell }+\xi )$ for all $\ell \ge 0$. Compared to the standard starting point, this shift usually preserves the difficulty of the problem. In the second run, the three best solvers from the first run try to solve all test problems with an increased time limit of 1800 s.

• In the third run, the initial point $x^0$ is the standard starting point. The three best solvers from the first run try to solve the 98 test problems unsolved in the first run without the shift (46). Maximal time in sec increased from 300 to 7200 s and maximum number of nf2g increased from $20n+10000$ to $50n+200000$. In this case, the three best solvers from the first run succeeded to solve many of these unsolved problems. Test problems unsolved in third run could not be solved by any solver, even with a huge budget.

5.2 Default parameters for LMBOPT

For our tests we used for LMBOPT the following tuning parameters

$\mathtt{nsmin}=1$;	$\mathtt{nwait}=1$;	$\mathtt{rfac}=2.5$;	$\mathtt{nlf}=2$;	$\varDelta _m=10^{-13}$;	$\varDelta _{pg}=\varepsilon _m$;
$\varDelta _{H}=\varepsilon _m$;	$\varDelta _{\alpha }=5\varepsilon _m$;	$l^{\max }=4$;	$\beta =0.02$;	$\beta ^{\mathtt{CG}}=0.001$;	$\varDelta _{\mathop {\mathrm {a}}}=10^{-12}$;
$\varDelta _{reg}=10^{-12}$;	$\varDelta _w=\varepsilon _m$;	$\mathtt{facf}=10^{-8}$;	$\varDelta _x=10^{-20}$;	$m=12$;	$\mathtt{mf}=2$;
$\mathtt{typeH}=0$;	$\mathtt{nnulmax}=3$;	$\mathtt{del}=10^{-10}$;	$\varDelta _r=20$;	$\varDelta _g=100$;	$\varDelta _{b}=10\varepsilon _m$;
$\varDelta _u=1000$;	$\theta =10^{-8}$;	$\mathtt{exact}=0$;	$\varDelta _{po}=\varepsilon _m$;	$\mathtt{nstuckmax}=+\infty$;	$\zeta ^{\min }=-10^{50}$;
$\zeta ^{\max }=-10^{-50}$;	$\varDelta _D=10^{10}$;	$q^{\min }=2.5$;	$\varDelta _q=10$;	$\varDelta _f=2$;	$q=25$;
$\mathtt{mdf}=20$.

They are based on a limited tuning by hand. In a further release we plan to find optimal tuning parameters [48], as the quality of LMBOPT depends on it.

5.3 Codes compared

We compare LMBOPT with competitive solvers for unconstrained and bound constrained optimization. These solvers are

ASACG [40,41,42, 44],	CGdescent [40, 41, 44],	ASABCP [18],
SPG [8, 9],	LBFGSB [12],	LMBFG-DDOGL [11],
LMBFG-EIG-MS-2-2 [11],	LMBFG-BWX-MS [11],	LMBFG-EIG-inf-2 [11],
LMBFGS-TR [11],	LMBFG-MTBT [11],	LMBFG-MT [11],
LMBFG-EIG-MS [11],	LMBFG-EIG-curve-inf [11].

Details about the solvers and options used can be found in Sect. 1 of suppMat.pdf. For some solvers, we have chosen options other than the default ones to make them more competitive.

We only compare public software with an available Matlab interface. LANCELOT-B combines a trust region approach with projected gradient directions. But since there was no mex-file to run LANCELOT-B in Matlab, we could not call and run it in our Matlab environment. Similarly, we could not find a version of GENCAN, the bound constrained version of ALGENCAN [7], which could be handled in Matlab. GENCAN is a combination of spectral projected gradient and an active set strategy. It is unlikely to introduce significant bias in the comparison. Hence, we compare LMBOPT to many known solvers using various active set strategies and either projected conjugate gradient methods, projected truncated Newton methods, or projected quasi Newton methods.

Unconstrained solvers were turned into bound-constrained solvers by pretending that the reduced gradient at the point $\pi [x]$ is the requested gradient at x. Therefore no theoretical analysis is available, but the results show that this is a simple and surprisingly effective strategy.

5.4 The results for stringent resources

5.4.1 Unconstrained and bound constrained optimization problems

We tested all 15 solvers for problems in dimension 1 to 100001. A list of problems unsolved by all solvers can be found in Sect. 4 of suppMat.pdf.

For more refined statistics, we use our test environment (Kimiaei and Neumaier [48]) for comparing optimization routines on the CUTEst test problem collection.

For a given collection ${\mathcal {S}}$ of solvers and a collection ${\mathcal {P}}$ of problems, the efficiency of the solver so for solving the problem $j\in {\mathcal {P}}$ with respect to the cost measure $c_s$ is the strength of the solver $so \in {\mathcal {S}}$ – relative to an ideal solver that matches on each problem the best solver. It is measured by

$$\begin{aligned} e^j_{so}{:}{=}\left\{ \begin{array}{ll}\displaystyle \min _{s\in S}c_{s}/c_{so},~~~ &{} \hbox {if the solver { so} solved the problem} j\in {\mathcal {P}},\\ 0,~~~ &{} \hbox {otherwise}. \end{array} \right. \end{aligned}$$

The total mean efficiency of the solver so with respect to $c_s$ is defined by

$$\begin{aligned} e_{so} = \displaystyle \mathop {\mathrm {mean}}_{j\in {\mathcal {P}}}(e^j_{so}). \end{aligned}$$

$T_{\mathop {\mathrm {mean}}}$ is the mean of the time in seconds needed by a solver to solve the test problems chosen from the list of test problems ${\mathcal {P}}$, ignoring the times for unsolved problems. #100 is the total number of problems for which no other solver was strictly better than the solver so with respect to nf2g ($e^j_{so}=1=100\%$). !100 is the total number of problems for which the solver so was strictly better than all other solvers with respect to nf2g.

In the tables, efficiencies are given in percent. Larger efficiencies in the table imply a better average behaviour; a zero efficiency indicates failure. All values are rounded (towards zero) to whole integers. Mean efficiencies are taken over the 990 problems tried by all solvers and solved by at least one of them, out of a total of 1088 problems. The columns titled “# of anomalies” report statistic on failure reasons:

• n indicates that nf2g $\ge 20n+10000$ was reached.

• t indicates that sec $\ge 300$ was reached.

• f indicates that the algorithm failed for other reasons.

As can be seen from Table 1 and Figs. 2, 3 and 4, LMBOPT stands out as the most robust solver for unconstrained and bound constrained optimization problems; it is the best in terms of number of solved problems and the ng efficiency. Other best solvers in terms of the number of solved problems and the nf2g efficiency are ASACG and LMBFG-EIG-MS, respectively. LBFGSB is the best in terms of number of function evaluations #100 and !100, but it is not comparable to other algorithms in terms of the number of solved problems.

Table 1 The summary results for all problems

5.4.2 Classified by constraints and dimensions

Results for the three best solvers for all problems classified by dimension and constraint are given in Table 2, Figs. 5, 6, 7, 8, 9 and 10, and Box plots 11, 12, 13, 14, 15 and 16. These results show that,

• for low-dimensional problems ($1\le n\le 30$), (1) LMBOPT is the best solver in terms of the ng and nf2g efficiencies and the number of solved problems, (2) LMBFG-EIG-MS is the best solver in terms of the nf efficiency (for both unconstrained and bound constrained problems), and (3) ASACG is the second best solver in terms of the number of solved problems (for both unconstrained and bound constrained problems);

• for medium-dimensional problems ($31\le n\le 500$), (1) LMBOPT is the best in terms of the ng efficiency and the number of solved problems in the both unconstrained and bound constrained problems. It is the best is the best in terms of the nf2g efficiency for the unconstrained problems, (2) LMBFG-EIG-MS is the best in terms of nf for the both unconstrained and bound constrained problems and nf2g for the bound constrained problems only, (3) ASACG is the best solver in terms of the nf2g efficiency for the bound constrained problems;

• for large-dimensional problems ($501\le n\le 100001$), (1) LMBOPT is the best solver in terms of the ng efficiency for both unconstrained and bound constrained problems, (2) LMBFG-EIG-MS is the best solver in terms of the nf and nf2g efficiencies and the number of solved problems (for all problems) and is the best solver in terms of the number of solved problems (for bound constrained problems), (3) ASACG is the best solver in terms of the number of solved problems for the unconstrained problems only.

• for all problems ($1\le n \le 100001$), (1) LMBOPT is the best in terms of the number of solved problems and the ng efficiency in both unconstrained and bound constrained problems, (2) LMBFG-EIG-MS is the best solver in terms of the nf and nf2g efficiencies for both unconstrained and bound constrained problems.

Table 2 The summary results classified by dimension and constraint for all problems

5.5 Results for hard problems

All solvers have been run again on the hard problems defined as the 98 test problems unsolved in the first run. In this case, the standard starting point was used instead of (46) and both nfmax and secmax were increased. 41 test problems were not solved by all solvers for dimensions 1 up to 100001, given in Table 3.

From Table 4 and Figs. 17, 18 and 19, we conclude

• LMBOPT is the best in terms of the number of solved problems and the ng and nf2g efficiencies for the hard bound constrained problems.

• ASACG is the best in terms of the number of solved problems and the ng and nf2g efficiencies for the hard unconstrained problems.

• LMBFG-EIG-MS is the best in terms of the ng and nf2g efficiencies for the hard unconstrained problems.

Table 3 The hard problems unsolved by all solvers

Table 4 The summary results for hard problems

Fig. 20

a Flow chart for unconstrained problems classified by problems. b Flow chart for bound constrained problems classified by the problem dimension. c Flow chart for hard problems classified by constraint. Here L-E-M stands for LMBFG-EIG-MS

5.6 Recommendations

In this section, we recommend a solver choice based on our findings. The choice depends on the problem dimension, the presence or absence of constrains, the desired robustness, and the relative costs of the function and gradient evaluations shown in Subfigures (a)–(c) of Fig. 20.