Abstract
We present DFO-GN, a derivative-free version of the Gauss–Newton method for solving nonlinear least-squares problems. DFO-GN uses linear interpolation of residual values to build a quadratic model of the objective, which is then used within a typical derivative-free trust-region framework. We show that DFO-GN is globally convergent and requires at most \({\mathcal {O}}(\epsilon ^{-2})\) iterations to reach approximate first-order criticality within tolerance \(\epsilon \). We provide an implementation of DFO-GN and compare it to other state-of-the-art derivative-free solvers that use quadratic interpolation models. We demonstrate numerically that despite using only linear residual models, DFO-GN performs comparably to these methods in terms of objective evaluations. Furthermore, as a result of the simplified interpolation procedure, DFO-GN has superior runtime and scalability. Our implementation of DFO-GN is available at https://github.com/numericalalgorithmsgroup/dfogn (https://doi.org/10.5281/zenodo.2629875).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Over the last 15–20 years, there has been a resurgence and increased effort devoted to developing efficient methods for derivative-free optimization (DFO)—that is, optimizing an objective using only function values. These methods are useful to many applications [9], for instance, when the objective function is a black-box function or legacy code (meaning manual computation of derivatives or algorithmic differentiation is impractical), has stochastic noise (so finite differencing is inaccurate) or expensive to compute (so the evaluation of a full n-dimensional gradient is intractable). There are several popular classes of DFO methods, such as direct and pattern search, model-based and evolutionary algorithms [11, 17, 24, 28]. Here, we consider model-based methods, which capture curvature in the objective well [11] and have been shown to have good practical performance [20].
Model-based methods typically use a trust-region framework for selecting new iterates, which ensures global convergence, provided we can build a sufficiently accurate model for the objective [5]. The model-building process most commonly uses interpolation of quadratic functions, as originally proposed by Winfield [36] and later developed by Conn, Scheinberg and Toint [6, 10] and Powell [23, 25]. Another common choice for model-building is to use radial basis functions [22, 34]. Global convergence results exist in both cases [8, 9, 35]. Several codes for model-based DFO are available, including those by Powell [39] and others (see e.g. [9, 11] and references therein).
Summary of contributions In this work, we consider nonlinear least-squares minimization, without constraints in the theoretical developments but allowing bounds in the implementation. Model-based DFO is naturally suited to exploit problem structure, and in this work we propose a method inspired by the classical Gauss–Newton method for derivative-based optimization (e.g. [21, Chapter 10]). This method, which we call DFO-GN (Derivative-Free Optimization using Gauss–Newton), constructs linear interpolants for each residual, requiring exactly \(n+1\) points on each iteration,Footnote 1 and yielding an approximate quadratic local model for the least-squares objective. This approach was considered by the framework of Zhang, Conn and Scheinberg [38], but their numerical results rely on (partial or full) quadratic local models for each residual. In addition to proving theoretical guarantees for DFO-GN in terms of global convergence and worst-case complexity, we provide an implementation that is a modification of Powell’s BOBYQA [29] which we extensively test and compare with existing state of the art DFO solvers. Our numerical results show that little to nothing is lost by our simplified approach in terms of algorithm performance on a given evaluation budget, when applied to smooth and noisy, zero- and non-zero residual problems. Furthermore, significant gains are made in terms of reduced computational cost of the interpolation problem and memory costs of storing the models. Thus DFO-GN exhibits improved scalability compared to methods using quadratic residual models, although more work is needed to match the scalability of derivative-based methods. When the high computational cost of evaluations is more of a concern than scalability, DFO-GN still offers the advantage of a reduced evaluation cost for the initialization, again due to choosing a smaller interpolation set, without loss in overall performance. For these reasons, this paper advocates for the use of linear residual models for nonlinear least-squares problems in a derivative-free setting, and provides a theoretically-justified and practical implementation to achieve this.
Relevant existing literature An early work in this direction is [30], which uses linear models interpolated using the last \(n+1\) iterates, but it has no globalization mechanism (trust region, linesearch, etc.) and no convergence guarantees. More recently, in [38], each residual function is approximated by a quadratic interpolating model, using function values from \(p\in [n+1, (n+1)(n+2)/2]\) points. A quadratic model for the overall least-squares objective is built from the models for each residual function, that takes into account full quadratic terms in the models asymptotically but allows the use of simpler models early on in the run of the algorithm. The DFBOLS implementation in [38], which, strictly speaking, does not allow linear models (requiring \(n+2\le p\le (n+1)(n+2)/2\)), is shown to perform better than Powell’s BOBYQA on a standard least-squares test set; only results for the choice \(p=2n+1\) are presented in [38]. A quadratic asymptotic convergence rate for zero-residual problems is proved for this framework in [37]. We note that BOBYQA is for general minimization and uses a quadratic model for the objective with the same requirement on p as DFBOLS, namely \(n+2\le p\le (n+1)(n+2)/2\).
A similar derivative-free framework for nonlinear least-squares problems is POUNDERS by Wild [33], which constructs adaptive interpolation models for each residual, depending on the number of points and evaluations available, and incorporates all of these residual models into the objective’s model on each iteration. More specifically, at each iteration it constructs models using \(n+1\le p \le p_{max}\) points, where p is chosen dynamically at each iteration and where \(p_{max}\in [n+2, (n+1)(n+2)/2]\) is a user input. Since the model for each residual is based on a minimum Frobenius change to the model Hessian, POUNDERS essentially uses linear models in at least its first iteration, and once \(p>n+1\) on some iteration, quadratic models are constructed and used for that and all subsequent iterations. In its implementation, it allows parallel computation of each residual component, and accepts previously-computed evaluations as an input, thus providing extra information to the solver.
We also note the connection to [3], which considers a Levenberg–Marquardt method for nonlinear least-squares when gradient evaluations are noisy; the framework is that of probabilistic local models, and it uses a regularization parameter rather than trust region to ensure global convergence. The algorithm is applied and further developed for data assimilation problems, with careful quantification of noise and algorithm parameters. Using linear vector models for objectives which are a composition of a (possibly nonconvex) vector function with a (possibly nonsmooth) convex function, such as a sum of squares, was also considered in [12]. There, worst-case complexity bounds for a general model-based trust-region DFO method applied to such objectives are established. Our approach differs in that it is designed specifically for nonlinear least-squares, and uses an algorithmic framework that is much closer to the software of Powell [29]. Finally, we note a mild connection to the approach in [1], where multiple solutions to nonlinear inverse problems are sought by means of a two-phase method, where in the first phase, low accuracy solutions are obtained by building a linear regression model from a (large) cloud of points and moving each point to its corresponding, slightly perturbed, Gauss–Newton step.
Further details of contributions In terms of theoretical guarantees, we extend the global convergence results in [38], which apply to linear residual models, by proving first-order global convergence, namely, that any (not just one) limit point of the iterates  is stationary. We also provide a worst-case complexity analysis with an iteration count which matches that of Garmanjani, Júdice and Vicente [12] in the order of the accuracy, but with problem constants that correspond to second-order methods. This reflects the fact that we capture some of the curvature in the objective (since linear models for residuals still give an approximate quadratic model for the least-squares objective), and so the complexity of DFO-GN sits between first- and second-order methods.
is stationary. We also provide a worst-case complexity analysis with an iteration count which matches that of Garmanjani, Júdice and Vicente [12] in the order of the accuracy, but with problem constants that correspond to second-order methods. This reflects the fact that we capture some of the curvature in the objective (since linear models for residuals still give an approximate quadratic model for the least-squares objective), and so the complexity of DFO-GN sits between first- and second-order methods.
In the DFO-GN implementation, the simplification from quadratic to linear residual models leads to a confluence of two approaches for analysing and improving the geometry of the interpolation set. We compare DFO-GN to Powell’s general DFO solver BOBYQA and to least-squares DFO solvers DFBOLS [38] (Fortran), POUNDERS [33] and our Python DFBOLS re-implementation Py-DFBOLS. Compared to DFBOLS, Py-DFBOLS uses matrix factorization to solve the interpolation problem (rather than low-rank updating) which, along with its implementation language, means it more closely matches the approach of DFO-GN and hence can be directly compared in terms of runtime and memory usage. The primary test set is Moré & Wild [20] where additionally, we also consider noisy variants for each problem, perturbing the test set appropriately with unbiased Gaussian (multiplicative and additive), and with additive \(\chi ^2\) noise; we solve to both low and high accuracy requirements for given evaluation budgets. We find—and show by means of performance and data profiles—that DFO-GN performs comparably well in terms of objective evaluations to the best of solvers for zero and nonzero residual problems, albeit with a small penalty for objectives with additive stochastic noise. We then do a runtime comparison between DFO-GN and Py-DFBOLS on the same test set and settings, comparing like for like, and find that DFO-GN is at least 7 times faster; see Table 1 for details. We further investigate scalability features of DFO-GN. We compare memory requirements and per-iteration runtime for DFO-GN and DFBOLS on a particular nonlinear equation problem from CUTEst with growing problem dimension n; we find that both of these increase much more rapidly for the latter solver than the former (for example, for \(n=2500\) DFO-GN’s per-iteration runtime is 2.5 times faster than the Fortran DFBOLS’ for \(n=1400\)). To further illustrate that the improved scalability of DFO-GN does not come at the cost of performance, we compare evaluation performance of DFO-GN and DFBOLS on 60 medium-size least-squares problems from CUTEst and find similarly good behaviour of DFO-GN as on the Moré & Wild set.
Implementation Our Python implementation of DFO-GN is available on GitHub,Footnote 2 and is released under the open-source GNU General Public License.
Structure of paper In Sect. 2 we state the DFO-GN algorithm. We prove its global convergence to first-order critical points and worst case complexity in Sect. 3. Then we discuss the differences between this algorithm and its software implementation in Sect. 4. Lastly, in Sect. 5, we compare DFO-GN to other model-based derivative-free least-squares solvers on a selection of test problems, including noisy and higher-dimensional problems. We draw our conclusions in Sect. 6.
2 DFO-GN Algorithm
Here, our focus is unconstrained nonlinear least-squares minimization

where  maps \({\mathbb {R}}^n\rightarrow {\mathbb {R}}^m\) and is continuously differentiable with \(m\times n\) Jacobian matrix
maps \({\mathbb {R}}^n\rightarrow {\mathbb {R}}^m\) and is continuously differentiable with \(m\times n\) Jacobian matrix  , although these derivatives are not available. Typically \(m\ge n\) in practice, but we do not require this for our method. Throughout, \(\Vert \cdot \Vert \) refers to the Euclidean norm for vectors or largest singular value for matrices, unless otherwise stated, and we define
, although these derivatives are not available. Typically \(m\ge n\) in practice, but we do not require this for our method. Throughout, \(\Vert \cdot \Vert \) refers to the Euclidean norm for vectors or largest singular value for matrices, unless otherwise stated, and we define  to be the closed ball of radius \(\varDelta >0\) about
to be the closed ball of radius \(\varDelta >0\) about  .
.
In this section, we introduce the DFO-GN algorithm for solving (2.1) using linear interpolating models for \(\mathbf {r}\).
2.1 Linear residual models
In the classical Gauss–Newton method, we approximate \(\mathbf {r}\) in the neighbourhood of an iterate  by its linearization:
by its linearization:  , where
, where  is the Jacobian matrix of first derivatives of \(\mathbf {r}\). For DFO-GN, we use a similar approximation, but replace the Jacobian with an approximation to it calculated by interpolation.
is the Jacobian matrix of first derivatives of \(\mathbf {r}\). For DFO-GN, we use a similar approximation, but replace the Jacobian with an approximation to it calculated by interpolation.
Assume at iteration k we have a set of \(n+1\) interpolation points  in \({\mathbb {R}}^n\) at which we have evaluated \(\mathbf {r}\). This set always includes the current iterate; for simplicity of notation, we assume
in \({\mathbb {R}}^n\) at which we have evaluated \(\mathbf {r}\). This set always includes the current iterate; for simplicity of notation, we assume  . We then build the model
. We then build the model

by finding the unique \(J_k\in {\mathbb {R}}^{m\times n}\) satisfying the interpolation conditions

noting that the other interpolation condition  is automatically satisfied by (2.2).Footnote 3 We can find \(J_k\) by solving the \(n\times n\) system
is automatically satisfied by (2.2).Footnote 3 We can find \(J_k\) by solving the \(n\times n\) system

for each \(i=1,\ldots ,m\), where the rows of \(J_k\) are  . This system is invertible whenever the set of vectors
. This system is invertible whenever the set of vectors  is linearly independent. We ensure this in the algorithm by routines which improve the geometry of \(Y_k\) (in a specific sense to be discussed in Sect. 2.3).
is linearly independent. We ensure this in the algorithm by routines which improve the geometry of \(Y_k\) (in a specific sense to be discussed in Sect. 2.3).
Having constructed the linear models for each residual (2.1), we need to construct a model for the full objective f. To do this we simply take the sum of squares of the residual models, namely,

where  and \(H_k:=J_k^{\top }J_k\).
and \(H_k:=J_k^{\top }J_k\).
2.2 Trust region framework
The DFO-GN algorithm is based on a trust-region framework [5]. In such a framework, we use our model for the objective (2.5), and maintain a parameter \(\varDelta _k>0\) which characterizes the region in which we ‘trust’ our model to be a good approximation to the objective; the resulting ‘trust region’ is  . At each iteration, we use our model to find a new point where we expect the objective to decrease, by (approximately) solving the ‘trust region subproblem’
. At each iteration, we use our model to find a new point where we expect the objective to decrease, by (approximately) solving the ‘trust region subproblem’

If this new point  gives a sufficient objective reduction, we accept the step (
gives a sufficient objective reduction, we accept the step ( ), otherwise we reject the step (
), otherwise we reject the step ( ). We also use this information to update the trust region radius \(\varDelta _k\). The measure of ‘sufficient objective reduction’ is the ratio
). We also use this information to update the trust region radius \(\varDelta _k\). The measure of ‘sufficient objective reduction’ is the ratio

This framework applies to both derivative-based and derivative-free settings. However in a DFO setting, we also need to update the interpolation set \(Y_k\) to incorporate the new point  , and have steps to ensure the geometry of \(Y_k\) does not become degenerate (see Sect. 2.3).
, and have steps to ensure the geometry of \(Y_k\) does not become degenerate (see Sect. 2.3).
A minimal requirement on the calculation of  to ensure global convergence is the following.
to ensure global convergence is the following.
Assumption 2.1
Our method for solving (2.6) gives a step  satisfying the sufficient (‘Cauchy’) decrease condition
satisfying the sufficient (‘Cauchy’) decrease condition

for some \(c_1\in [1/2, 1]\) independent of k.
This standard condition is not onerous, and can be achieved with \(c_1=1/2\) by one iteration of steepest descent with exact linesearch applied to the model \(m_k\) [5].
2.3 Geometry considerations
It is crucial that model-based DFO algorithms ensure the geometry of \(Y_k\) does not become degenerate; an example where ignoring geometry causes algorithm failure is given by Scheinberg and Toint [31].
To describe the notion of ‘good’ geometry, we need the Lagrange polynomials of \(Y_k\). In our context of linear approximation, the Lagrange polynomials are the basis  for the \((n+1)\)-dimensional space of linear functions on \({\mathbb {R}}^n\) defined by
for the \((n+1)\)-dimensional space of linear functions on \({\mathbb {R}}^n\) defined by

Such polynomials exist whenever the matrix in (2.4) is invertible [9, Lemma 3.2]; when this condition holds, we say that \(Y_k\) is poised for linear interpolation.
The notion of geometry quality is then given by the following [7].
Definition 2.2
(\(\varLambda \)-poised) Suppose \(Y_k\) is poised for linear interpolation. Let \(B\subset {\mathbb {R}}^n\) be some set, and \(\varLambda \ge 1\). Then we say that \(Y_k\) is \(\varLambda \)-poised in B if \(Y_k\subset B\) and

where  are the Lagrange polynomials for \(Y_k\).
are the Lagrange polynomials for \(Y_k\).
In general, if \(Y_k\) is \(\varLambda \)-poised with a small \(\varLambda \), then \(Y_k\) has ‘good’ geometry, in the sense that linear interpolation using points \(Y_k\) produces a more accurate model. The notion of model accuracy we use is given in [7, 8]:
Definition 2.3
(Fully linear, scalar function) A model \(m_k\in C^1\) for \(f\in C^1\) is fully linear in  if
if


for all  , where \(\kappa _{ef}\) and \(\kappa _{eg}\) are independent of
, where \(\kappa _{ef}\) and \(\kappa _{eg}\) are independent of  ,
,  and \(\varDelta _k\).
and \(\varDelta _k\).
In the case of a vector model, such as (2.1), we use an analogous definition as in [15], which is equivalent, up to a change in constants, to the definition in [12].
Definition 2.4
(Fully linear, vector function) A vector model  for
for  is fully linear in
is fully linear in  if
if


for all  , where \(J^m\) is the Jacobian of
, where \(J^m\) is the Jacobian of  , and \(\kappa _{ef}^r\) and \(\kappa _{eg}^r\) are independent of
, and \(\kappa _{ef}^r\) and \(\kappa _{eg}^r\) are independent of  ,
,  and \(\varDelta _k\).
and \(\varDelta _k\).
In Sect. 3.1, we show that if \(Y_k\) is \(\varLambda \)-poised, then  (2.1) and \(m_k\) (2.5) are fully linear in
(2.1) and \(m_k\) (2.5) are fully linear in  , with constants that depend on \(\varLambda \).
, with constants that depend on \(\varLambda \).
2.4 Full algorithm specification
A full description of the DFO-GN algorithm is provided in Algorithm 1.
In each iteration, if  is small, we apply a ‘criticality phase’. This ensures that \(\varDelta _k\) is comparable in size to
is small, we apply a ‘criticality phase’. This ensures that \(\varDelta _k\) is comparable in size to  , which makes \(\varDelta _k\), as well as
, which makes \(\varDelta _k\), as well as  , a good measure of progress towards optimality. After computing the trust region step
, a good measure of progress towards optimality. After computing the trust region step  , we then apply a ‘safety phase’, also originally from Powell [26]. In this phase, we check if
, we then apply a ‘safety phase’, also originally from Powell [26]. In this phase, we check if  is too small compared to the lower bound \(\rho _k\) on the trust-region radius (see below), and if so we reduce \(\varDelta _k\) and improve the geometry of \(Y_k\), without evaluating
is too small compared to the lower bound \(\rho _k\) on the trust-region radius (see below), and if so we reduce \(\varDelta _k\) and improve the geometry of \(Y_k\), without evaluating  . The intention of this step is to detect situations where our trust region step will likely not provide sufficient function decrease without evaluating the objective, which would be wasteful. If the safety phase is not called, we evaluate
. The intention of this step is to detect situations where our trust region step will likely not provide sufficient function decrease without evaluating the objective, which would be wasteful. If the safety phase is not called, we evaluate  and determine how good the trust region step was, accepting any point which achieved sufficient objective decrease. There are two possible causes for the situation \(R_k<\eta _1\) (i.e. the trust region step was ‘bad’): the interpolation set is not good enough, or \(\varDelta _k\) is too large. We first check the quality of the interpolation set, and only reduce \(\varDelta _k\) if necessary.
and determine how good the trust region step was, accepting any point which achieved sufficient objective decrease. There are two possible causes for the situation \(R_k<\eta _1\) (i.e. the trust region step was ‘bad’): the interpolation set is not good enough, or \(\varDelta _k\) is too large. We first check the quality of the interpolation set, and only reduce \(\varDelta _k\) if necessary.
An important feature of DFO-GN, due to Powell [26], is that it maintains not only the (usual) trust region radius \(\varDelta _k\) (used in (2.6) and in checking \(\varLambda \)-poisedness), but also a lower bound on it, \(\rho _k\). This mechanism is useful when we reject the trust region step, but the geometry of \(Y_k\) is not good (the ‘Model Improvement Phase’). In this situation, we do not want to shrink \(\varDelta _k\) too much, because it is likely that the step was rejected because of the poor geometry of \(Y_k\), not because the trust region was too large. The algorithm floors \(\varDelta _k\) at \(\rho _k\), and only shrinks \(\varDelta _k\) when we reject the trust region step and the geometry of \(Y_k\) is good (so the model \(m_k\) is accurate)—in this situation, we know that reducing \(\varDelta _k\) will actually be useful.

Remark 2.5
There are two different geometry-improving phases in Algorithm 1. The first modifies \(Y_k\) to ensure it is \(\varLambda \)-poised in  , and is called in the safety and model improvement phases. This can be achieved by [9, Algorithm 6.3], for instance, where the number of interpolation systems (2.4) to be solved depends only on \(\varLambda \) and n [9, Theorem 6.3].
, and is called in the safety and model improvement phases. This can be achieved by [9, Algorithm 6.3], for instance, where the number of interpolation systems (2.4) to be solved depends only on \(\varLambda \) and n [9, Theorem 6.3].
The second, called in the criticality phase, also ensures \(Y_k\) is \(\varLambda \)-poised, but it also modifies \(\varDelta _k\) to ensure  . This is a more complicated procedure [9, Algorithm 10.2], as we have a coupling between \(\varDelta _k\) and \(Y_k\): ensuring \(\varLambda \)-poisedness in
. This is a more complicated procedure [9, Algorithm 10.2], as we have a coupling between \(\varDelta _k\) and \(Y_k\): ensuring \(\varLambda \)-poisedness in  depends on \(\varDelta _k\), but since
depends on \(\varDelta _k\), but since  depends on \(Y_k\), there is a dependency of \(\varDelta _k\) on \(Y_k\). Full details of how to achieve this are given in Appendix B—we show that this procedure terminates as long as
depends on \(Y_k\), there is a dependency of \(\varDelta _k\) on \(Y_k\). Full details of how to achieve this are given in Appendix B—we show that this procedure terminates as long as  . In addition, there, we also prove the bound
. In addition, there, we also prove the bound

If the procedure terminates in one iteration, then \(\varDelta _k=\varDelta _k^{init}\), and we have simply made \(Y_k\)\(\varLambda \)-poised, just as in the model-improving phase. Otherwise, we do one of these model-improving iterations, then several iterations where both \(\varDelta _k\) is reduced and \(Y_k\) is made \(\varLambda \)-poised. The bound (2.16) tells us that these unsuccessful-type iterations do not occur when \(\varDelta _k^{init}\) (but not  ) is sufficiently small.Footnote 4
) is sufficiently small.Footnote 4
Remark 2.6
In Lemma 3.3, we show that if \(Y_k\) is \(\varLambda \)-poised, then \(m_k\) is fully linear with constants that depend on \(\varLambda \). For the highest level of generality, one may replace ‘make \(Y_k\)\(\varLambda \)-poised’ with ‘make \(m_k\) fully linear’ throughout Algorithm 1. Any strategy which achieves fully linear models would be sufficient for the convergence results in Sect. 3.3.
Remark 2.7
There are several differences between Algorithm 1 and its implementation, which we fully detail in Sect. 4. In particular, there is no criticality phase in the DFO-GN implementation as we found it is not needed, but the safety step is preserved to keep continuity with the BOBYQA frameworkFootnote 5; also, the geometry-improving phases are replaced by a simplified calculation.
3 Convergence and complexity results
We first outline the connection between \(\varLambda \)-poisedness of \(Y_k\) and fully linear models. We then prove global convergence of Algorithm 1 (i.e. convergence from any starting point  ) to first-order critical points, and determine its worst-case complexity.
) to first-order critical points, and determine its worst-case complexity.
3.1 Interpolation models are fully linear
To begin, we require some assumptions on the smoothness of  .
.
Assumption 3.1
The function  is \(C^1\) and its Jacobian
is \(C^1\) and its Jacobian  is Lipschitz continuous in \({\mathcal {B}}\), the convex hull of
is Lipschitz continuous in \({\mathcal {B}}\), the convex hull of  , with constant \(L_J\). We also assume that
, with constant \(L_J\). We also assume that  and
and  are uniformly bounded in the same region; i.e.
are uniformly bounded in the same region; i.e.  and
and  for all
for all  .
.
If the level set  is bounded, which is assumed in [38], then
is bounded, which is assumed in [38], then  for all k, so \({\mathcal {B}}\) is compact, from which Assumption 3.1 follows. A standard result follows, whose proof can be found in [4].
for all k, so \({\mathcal {B}}\) is compact, from which Assumption 3.1 follows. A standard result follows, whose proof can be found in [4].
Lemma 3.2
If Assumption 3.1 holds, then \(\nabla f\) is Lipschitz continuous in \({\mathcal {B}}\) with constant
We now state the connection between \(\varLambda \)-poisedness of \(Y_k\) and full linearity of the models  (2.1) and \(m_k\) (2.5).
(2.1) and \(m_k\) (2.5).
Lemma 3.3
Suppose Assumption 3.1 holds and \(Y_k\) is \(\varLambda \)-poised in  . Then
. Then  (2.1) is a fully linear model for
(2.1) is a fully linear model for  in
in  in the sense of Definition 2.4 with constants
in the sense of Definition 2.4 with constants
in (2.13) and (2.14), where \(C={\mathcal {O}}(\varLambda )\). Under the same hypotheses, \(m_k\) (2.5) is a fully linear model for f in  in the sense of Definition 2.3 with constants
in the sense of Definition 2.3 with constants
in (2.11) and (2.12), where \(L_{\nabla f}\) is from (3.1). We also have the bound \(\Vert H_k\Vert \le (\kappa _{eg}^r\varDelta _{max} + J_{max})^2\), independent of  , \(Y_k\) and \(\varDelta _k\).
, \(Y_k\) and \(\varDelta _k\).
Proof
See Appendix A. \(\square \)
3.2 Global convergence of DFO-GN
We begin with some nomenclature to describe certain iterations: we call an iteration (for which the safety phase is not called)
-
‘Successful’ if
 (i.e. \(R_k\ge \eta _1\)), and ‘very successful’ if \(R_k\ge \eta _2\). Let \({\mathcal {S}}\) be the set of successful iterations k;
(i.e. \(R_k\ge \eta _1\)), and ‘very successful’ if \(R_k\ge \eta _2\). Let \({\mathcal {S}}\) be the set of successful iterations k; -
‘Model-Improving’ if \(R_k<\eta _1\) and the model-improvement phase is called (i.e. \(Y_k\) is not \(\varLambda \)-poised in
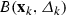 ); and
); and -
‘Unsuccessful’ if \(R_k<\eta _1\) and the model-improvement phase is not called.
The results below are largely based on corresponding results in [9, 38]. As such, we omit many details which can be found there; full proofs of these results are given in extended technical report [4] of this paper.
Assumption 3.4
We assume that \(\Vert H_k\Vert \le \kappa _H\) for all k, for some \(\kappa _H\ge 1\).Footnote 6
Lemma 3.5
(Lemma 4.3, [38]) Suppose Assumption 2.1 holds. If the model \(m_k\) is fully linear in  and
and

then either the k-th iteration is very successful or the safety phase is called.
The next result provides a lower bound on the size of the trust region step  , which we will later use to determine that the safety phase is not called when
, which we will later use to determine that the safety phase is not called when  is bounded away from zero and \(\varDelta _k\) is sufficiently small. Note that [38, Lemma 4.4] shows that the safety phase is not called by requiring that the trust region subproblem (2.6) is solved to global optimality, a stronger condition than Assumption 2.1.
is bounded away from zero and \(\varDelta _k\) is sufficiently small. Note that [38, Lemma 4.4] shows that the safety phase is not called by requiring that the trust region subproblem (2.6) is solved to global optimality, a stronger condition than Assumption 2.1.
Lemma 3.6
Suppose Assumption 2.1 holds. Then the step  satisfies
satisfies

where \(c_2 :=2c_1 / (1+\sqrt{1+2c_1})\).
Proof
Let \(h_k:=\max (\Vert H_k\Vert ,1)\ge 1\). Since  from (2.8), we have
from (2.8), we have

Substituting this into (2.8), we get

For (3.7) to be satisfied, we require that  is larger than (or equal to) the positive root of the left-hand side of (3.7), which gives the first inequality below
is larger than (or equal to) the positive root of the left-hand side of (3.7), which gives the first inequality below

where  ; from which we recover (3.5). \(\square \)
; from which we recover (3.5). \(\square \)
Lemma 3.7
In all iterations,  . Also, if
. Also, if  then
then

Proof
Firstly, if the criticality phase is not called, then we must have  . Otherwise, we have
. Otherwise, we have  . Hence
. Hence  . The proof of (3.9) is given in [9, Lemma 10.11]. \(\square \)
. The proof of (3.9) is given in [9, Lemma 10.11]. \(\square \)
Lemma 3.8
Suppose Assumptions 2.1, 3.1 and 3.4 hold. If  for all k, then \(\rho _k\ge \rho _{min} > 0\) for all k, where
for all k, then \(\rho _k\ge \rho _{min} > 0\) for all k, where
Proof
From Lemma 3.7, we also have  for all k. To find a contradiction, let k(0) be the first k such that \(\rho _k<\rho _{min}\). That is, we have
for all k. To find a contradiction, let k(0) be the first k such that \(\rho _k<\rho _{min}\). That is, we have
We first show that
From Algorithm 1, we know that either \(\rho _{k(0)}=\rho _{k(0)}^{init}\) or \(\rho _{k(0)}=\varDelta _{k(0)}\). Hence we must either have \(\rho _{k(0)}^{init}<\rho _{min}\) or \(\varDelta _{k(0)}<\rho _{min}\). In the former case, there is nothing to prove; in the latter, using Lemma B.1, we have that
Since \(\rho _{min} \le \omega _C \epsilon / (\kappa _{eg}+1/\mu )\), we therefore conclude that (3.12) holds.
Since \(\rho _{min}\le \varDelta _0^{init}=\rho _0^{init}\), we therefore have \(k(0)>0\) and \(\rho _{k(0)-1} \ge \rho _{min} > \rho _{k(0)}^{init}\). This reduction in \(\rho \) can only happen from a safety step or an unsuccessful step, and we must have \(\rho _{k(0)}^{init}=\alpha _1\rho _{k(0)-1}\), so \(\rho _{k(0)-1} \le \rho _{min}/\alpha _1\). If we had a safety step, we know  , but if we had an unsuccessful step, we must have
, but if we had an unsuccessful step, we must have  . Hence in either case, we have
. Hence in either case, we have

since \(\gamma _S<1\) and \(\gamma _{dec}<1\). Hence by Lemma 3.6 we have

Note that \(\rho _{min} \le \alpha _1 \epsilon _g / \kappa _H < (\alpha _1 c_2 \epsilon _g)/(\gamma _S \kappa _H)\), where in the last inequality we used the choice of \(\gamma _S\) in Algorithm 1. This inequality and the choice of \(\gamma _S\), together with (3.15), also imply
Then since \(\varDelta _{k_{(0)}-1} \le \epsilon _g/\kappa _H\), Lemma 3.6 gives us  and the safety phase is not called.
and the safety phase is not called.
If \(m_k\) is not fully linear, then we must have either a successful or model-improving iteration, so \(\rho _{k_{(0)}}^{init}=\rho _{k_{(0)}-1}\), contradicting (3.12). Thus \(m_k\) must be fully linear. Now suppose that

Then using full linearity, we have

contradicting (3.16). That is, (3.17) is false and so together with (3.16), we have (3.4). Hence Lemma 3.5 implies iteration \((k_0-1)\) was very successful (as we have already established the safety phase was not called), so \(\rho _{k_{(0)}}^{init}=\rho _{k_{(0)}-1}\), contradicting (3.12). \(\square \)
Our first convergence result considers the case where we have finitely-many successful iterations.
Lemma 3.9
Suppose Assumptions 2.1, 3.1 and 3.4 hold. If there are finitely many successful iterations, then \(\lim _{k\rightarrow \infty }\varDelta _k=\lim _{k\rightarrow \infty }\rho _k=0\) and  .
.
Proof
The proof follows [9, Lemma 10.8], except we have to consider the possibility of safety phases in two places. First, to show \(\varDelta _k\rightarrow 0\), we note that \(\varDelta _k\) is reduced by a factor \(\max (\alpha _2,\omega _S)<1\) in safety phases. Secondly, we use the observation: if the \(m_k\) is fully linear,  is sufficiently large, and \(\rho _k\le \varDelta _k\) are both sufficiently small, then Lemma 3.5 gives us either a very successful iteration or a safety step. In this case, a safety step is not called, because Lemma 3.6 implies
is sufficiently large, and \(\rho _k\le \varDelta _k\) are both sufficiently small, then Lemma 3.5 gives us either a very successful iteration or a safety step. In this case, a safety step is not called, because Lemma 3.6 implies  . \(\square \)
. \(\square \)
Lemma 3.10
(Lemma 10.9, [9]) Suppose Assumptions 2.1, 3.1 and 3.4 hold. Then \(\lim _{k\rightarrow \infty }\varDelta _k=0\) and so \(\lim _{k\rightarrow \infty }\rho _k=0\).
Proof
The proof of [9, Lemma 10.9] shows \(\varDelta _k\rightarrow 0\); since \(\rho _k\le \varDelta _k\), we conclude \(\rho _k\rightarrow 0\). \(\square \)
Theorem 3.11
Suppose Assumptions 2.1, 3.1 and 3.4 hold. Then

Proof
If \(|{\mathcal {S}}|<\infty \), then this follows from Lemma 3.9. Otherwise, it follows from Lemma 3.10 and Lemma 3.8. \(\square \)
Theorem 3.12
Suppose Assumptions 2.1, 3.1 and 3.4 hold. Then  .
.
Proof
If \(|{\mathcal {S}}|<\infty \), then the result follows from Lemma 3.9. Otherwise, the proof of [9, Theorem 10.13] applies, except for one modification: for \(k\in {\mathcal {K}}\) sufficiently large, iteration k is not unsuccessful, so must be a safety, successful or model-improving step. It cannot be a safety step by the same reasoning as in the proof of Lemma 3.9: since  for \(k\in {\mathcal {K}}\), and \(\varDelta _k\rightarrow 0\), if k sufficiently large then Lemma 3.6 implies that
for \(k\in {\mathcal {K}}\), and \(\varDelta _k\rightarrow 0\), if k sufficiently large then Lemma 3.6 implies that  . Hence iteration k must be successful or model-improving, and the remainder of the proof holds. \(\square \)
. Hence iteration k must be successful or model-improving, and the remainder of the proof holds. \(\square \)
3.3 Worst-case complexity
Next, we bound the number of iterations and objective evaluations until  . We know such a bound exists from Theorem 3.11. Let \(i_{\epsilon }\) be the last iteration before
. We know such a bound exists from Theorem 3.11. Let \(i_{\epsilon }\) be the last iteration before  for the first time.
for the first time.
Lemma 3.13
Suppose Assumptions 2.1, 3.1 and 3.4 hold. Let \(|{\mathcal {S}}_{i_{\epsilon }}|\) be the number of successful steps up to iteration \(i_{\epsilon }\). Then

where \(\epsilon _g\) is defined in (3.9), and \(\rho _{min}\) in (3.10).
Proof
For all \(k\in {\mathcal {S}}_{i_{\epsilon }}\), we have the sufficient decrease condition

Since  from Lemma 3.7 and \(\varDelta _k\ge \rho _k\ge \rho _{min}\) from Lemma 3.8, this means
from Lemma 3.7 and \(\varDelta _k\ge \rho _k\ge \rho _{min}\) from Lemma 3.8, this means

Summing (3.22) over all \(k\in {\mathcal {S}}_{i_{\epsilon }}\), and noting that  , we get
, we get

from which (3.20) follows. \(\square \)
We now need to count the number of iterations of Algorithm 1 which are not successful. Following [12], we count each iteration of the loop inside the criticality phase (Algorithm 2) as a separate iteration—in effect, one ‘iteration’ corresponds to one construction of the model \(m_k\) (2.5). We also consider separately the number of criticality phases for which \(\varDelta _k\) is not reduced (i.e. \(\varDelta _k=\varDelta _k^{init}\)). Counting until iteration \(i_{\epsilon }\) (inclusive), we let
-
\({\mathcal {C}}^M_{i_{\epsilon }}\) be the set of criticality phase iterations \(k\le i_{\epsilon }\) for which \(\varDelta _k\) is not reduced (i.e. the first iteration of every call of Algorithm 2—see Remark 2.5 for further details);
-
\({\mathcal {C}}^U_{i_{\epsilon }}\) be the set of criticality phase iterations \(k\le i_{\epsilon }\) where \(\varDelta _k\) is reduced (i.e. all iterations except the first for every call of Algorithm 2);
-
\({\mathcal {F}}_{i_{\epsilon }}\) be the set of iterations where the safety phase is called;
-
\({\mathcal {M}}_{i_{\epsilon }}\) be the set of iterations where the model-improving phase is called; and
-
\({\mathcal {U}}_{i_{\epsilon }}\) be the set of unsuccessful iterations.Footnote 7
Lemma 3.14
Suppose Assumptions 2.1, 3.1 and 3.4 hold. Then we have the bounds
where \(\alpha _3:=\max (\omega _C, \omega _S, \gamma _{dec}, \alpha _2)<1\) and \(\rho _{min}\) is defined in (3.10).
Proof
On each iteration \(k\in {\mathcal {C}}^U_{i_{\epsilon }}\), we reduce \(\varDelta _k\) by a factor of \(\omega _C\). Similarly, on each iteration \(k\in {\mathcal {F}}_{i_{\epsilon }}\) we reduce \(\varDelta _k\) by a factor of at least \(\max (\omega _S, \alpha _2)\), and for iterations in \({\mathcal {U}}_{i_{\epsilon }}\) by a factor of at least \(\max (\gamma _{dec},\alpha _2)\). On each successful iteration, we increase \(\varDelta _k\) by a factor of at most \({\overline{\gamma }}_{inc}\), and on all other iterations, \(\varDelta _k\) is either constant or reduced. Therefore, we must have
from which (3.24) follows.
After every call of the criticality phase, we have either a safety, successful or unsuccessful step, giving us (3.25). Similarly, after every model-improving phase, the next iteration cannot call a subsequent model-improving phase, giving us (3.26). \(\square \)
Assumption 3.15
The algorithm parameter \(\epsilon _C \ge c_3\epsilon \) for some constant \(c_3>0\).
Note that Assumption 3.15 can be easily satisfied by appropriate parameter choices in Algorithm 1.
Theorem 3.16
Suppose Assumptions 2.1, 3.1, 3.4 and 3.15 hold. Then the number of iterations \(i_{\epsilon }\) (i.e. the number of times a model \(m_k\) (2.5) is built) until  is at most
is at most

where \(c_4 :=\min \left( c_3, (1 + \kappa _{eg}\mu )^{-1}\right) \) and
Proof
From Assumption 3.15 and Lemma 3.7, we have \(\epsilon _g = c_4\epsilon \). Similarly, from Lemma 3.8 we have \(\rho _{min}=\min (\varDelta _0^{init}, c_5\epsilon )\). Thus using Lemma 3.14, we can bound the total number of iterations by
and so (3.29) follows from this and Lemma 3.13. \(\square \)
We can summarize our results as follows:
Corollary 3.17
Suppose Assumptions 2.1, 3.1, 3.4 and 3.15 hold. Then for \(\epsilon \in (0,1]\), the number of iterations \(i_{\epsilon }\) (i.e. the number of times a model \(m_k\) (2.5) is built) until  is at most \({\mathcal {O}}(\kappa _H \kappa _d^2 \epsilon ^{-2})\), and the number of objective evaluations until \(i_{\epsilon }\) is at most \({\mathcal {O}}(\kappa _H \kappa _d^2 n \epsilon ^{-2})\), where \(\kappa _d:=\max (\kappa _{ef},\kappa _{eg})={\mathcal {O}}(n L_J^2)\).
is at most \({\mathcal {O}}(\kappa _H \kappa _d^2 \epsilon ^{-2})\), and the number of objective evaluations until \(i_{\epsilon }\) is at most \({\mathcal {O}}(\kappa _H \kappa _d^2 n \epsilon ^{-2})\), where \(\kappa _d:=\max (\kappa _{ef},\kappa _{eg})={\mathcal {O}}(n L_J^2)\).
Proof
From Theorem 3.16, we have \(c_4^{-1}={\mathcal {O}}(\kappa _{eg})\) and so
To leading order, the number of iterations is
as required. In every type of iteration, we change at most \(n+1\) points, and so require no more than \(n+1\) evaluations. The result \(\kappa _d={\mathcal {O}}(n L_J^2)\) follows from Lemma 3.3. \(\square \)
Remark 3.18
Theorem 3.16 gives us a possible termination criterion for Algorithm 1—we loop until k exceeds the value (3.29) or until \(\rho _k \le \rho _{min}\). However, this would require us to know problem constants \(\kappa _{ef}\), \(\kappa _{eg}\) and \(\kappa _H\) in advance, which is not usually the case. Moreover, (3.29) is a worst-case bound and so unduly pessimistic.
Remark 3.19
In [12], the authors propose a different criterion to test whether the criticality phase should be entered:  rather than
rather than  as found here and in [9]. We are able to use our criterion because of Assumption 3.15. If this did not hold, we would have \(\epsilon _g \ll \epsilon \) and so \(\rho _{min}\ll \epsilon \), which would worsen the result in Theorem 3.16. In practice, Assumption 3.15 is reasonable, as we would not expect a user to prescribe a criticality tolerance much smaller than their desired solution tolerance.
as found here and in [9]. We are able to use our criterion because of Assumption 3.15. If this did not hold, we would have \(\epsilon _g \ll \epsilon \) and so \(\rho _{min}\ll \epsilon \), which would worsen the result in Theorem 3.16. In practice, Assumption 3.15 is reasonable, as we would not expect a user to prescribe a criticality tolerance much smaller than their desired solution tolerance.
The standard complexity bound for first-order methods is \({\mathcal {O}}(\kappa _H \kappa _d^2 \epsilon ^{-2})\) iterations and \({\mathcal {O}}(\kappa _H \kappa _d^2 n \epsilon ^{-2})\) evaluations [12], where \(\kappa _d={\mathcal {O}}(\sqrt{n})\) and \(\kappa _H=1\). Corollary 3.17 gives us the same count of iterations and evaluations, but the worse bounds \(\kappa _d={\mathcal {O}}(n)\) and \(\kappa _H={\mathcal {O}}(\kappa _d)\), coming from the least-squares structure (Lemma 3.3).
However, our model (2.5) is better than a simple linear model for f, as it captures some of the curvature information in the objective via the term \(J_k^TJ_k\). This means that DFO-GN produces models which are between fully linear and fully quadratic [9, Definition 10.4], which is the requirement for convergence of second-order methods. It therefore makes sense to also compare the complexity of DFO-GN with the complexity of second-order methods.
Unsurprisingly, the standard bound for second-order methods is worse in general, than for first-order methods, namely, \({\mathcal {O}}(\max (\kappa _H \kappa _d^2, \kappa _d^3) \epsilon ^{-3})\) iterations and \({\mathcal {O}}(\max (\kappa _H \kappa _d^2, \kappa _d^3) n^2 \epsilon ^{-3})\) evaluations [16], where \(\kappa _d = {\mathcal {O}}(n)\), to achieve second-order criticality for the given objective. Note that here \(\kappa _d:=\max (\kappa _{ef}, \kappa _{eg}, \kappa _{eh})\) for fully quadratic models. If \(\Vert \nabla ^2 f\Vert \) is uniformly bounded, then we would expect \(\kappa _H={\mathcal {O}}(\kappa _{eh})={\mathcal {O}}(\kappa _d)\).
Thus DFO-GN has the iteration and evaluation complexity of a first-order method, but the problem constants (i.e. dependency on n) of a second-order method. That is, assuming \(\kappa _H={\mathcal {O}}(\kappa _d)\) (as suggested by Lemma 3.3), DFO-GN requires \({\mathcal {O}}(n^3 \epsilon ^{-2})\) iterations and \({\mathcal {O}}(n^4 \epsilon ^{-2})\) evaluations, compared to \({\mathcal {O}}(n\epsilon ^{-2})\) iterations and \({\mathcal {O}}(n^2\epsilon ^{-2})\) evaluations for a first-order method, and \({\mathcal {O}}(n^3\epsilon ^{-3})\) iterations and \({\mathcal {O}}(n^5\epsilon ^{-3})\) evaluations for a second-order method.
Remark 3.20
In Lemma 3.3, we used the result \(C={\mathcal {O}}(\varLambda )\) whenever \(Y_k\) is \(\varLambda \)-poised, and wrote \(\kappa _{eg}\) in terms of C; see Appendix A for details on the provenance of C with respect to the interpolation system (2.3). Our approach here matches the presentation of the first- and second-order complexity bounds from [12, 16]. However, [9, Theorem 3.14] shows that C may also depend on n. Including this dependence, we have \(C={\mathcal {O}}(\sqrt{n}\,\varLambda )\) for DFO-GN and general first-order methods, and \(C={\mathcal {O}}(n^2 \varLambda )\) for general second-order methods (where C is now adapted for quadratic interpolation). This would yield the alternative bounds \(\kappa _d={\mathcal {O}}(n)\) for first-order methods, \({\mathcal {O}}(n^2)\) for DFO-GN and \({\mathcal {O}}(n^3)\) for second-order methods.Footnote 8 Either way, we conclude that the complexity of DFO-GN lies between first- and second-order methods.
Remark 3.21
(Discussion of Assumption 3.4) It is also important to note that when \(m_k\) is fully linear, we have an explicit bound \(\Vert {H}_{k}\Vert \le {\widetilde{\kappa }}_{H}={\mathcal {O}}(\kappa _d)\) from Lemma 3.3. This means that Assumption 3.4, which typically necessary for first-order convergence (e.g. [9, 12]), is not required for Theorem 3.11 and our complexity analysis. To remove the assumption, we need to change Algorithm 1 in two places:
-
1.
Replace the test for entering the criticality phase with
 (3.36)
(3.36) -
2.
Require the criticality phase to output \(m_k\) fully linear and \(\varDelta _k\) satisfying
 (3.37)
(3.37)
With these changes, the criticality phase still terminates, but instead of (B.1) we have
We can also augment Lemma 3.7 with the following, which can be used to arrive at a new value for \(\rho _{min}\).
Lemma 3.22
In all iterations,  . If
. If  then
then

Ultimately, we arrive at complexity bounds which match Corollary 3.17, but replacing \(\kappa _H\) with \({\widetilde{\kappa }}_{H}\). However, Assumption 3.4 is still necessary for Theorem 3.12 to hold.
4 Implementation
In this section, we describe the key differences between Algorithm 1 and its software implementation DFO-GN. These differences largely come from Powell’s implementation of BOBYQA [29] and are also features of DFBOLS, the implementation of the algorithm from Zhang et al. [38]. We also obtain a unified approach for analysing and improving the geometry of the interpolation set due to our particular choice of local Gauss–Newton-like models.
4.1 Geometry-improving phases
In practice, DFO algorithms are generally not run to very high tolerance levels, and so the asymptotic behaviour of such algorithms is less important than for other optimization methods. To this end, DFO-GN, like BOBYQA and DFBOLS, does not implement a criticality phase; but the safety step is implemented to encourage convergence.
In the geometry phases of the algorithm, we check the \(\varLambda \)-poisedness of \(Y_k\) by calculating all the Lagrange polynomials for \(Y_k\) (which are linear), then maximizing the absolute value of each in  . To modify \(Y_k\) to make it \(\varLambda \)-poised, we can repeat the following procedure [9, Algorithm 6.3]:
. To modify \(Y_k\) to make it \(\varLambda \)-poised, we can repeat the following procedure [9, Algorithm 6.3]:
-
1.
Select the point
 (
(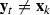 ) for which
) for which  is maximized (c.f. (2.10));
is maximized (c.f. (2.10)); -
2.
Replace
 in \(Y_k\) with
in \(Y_k\) with  , where
, where  (4.1)
(4.1)
until \(Y_k\) is \(\varLambda \)-poised in  . This procedure terminates after at most N iterations, where N depends only on \(\varLambda \) and n [9, Theorem 6.3], and in particular does not depend on
. This procedure terminates after at most N iterations, where N depends only on \(\varLambda \) and n [9, Theorem 6.3], and in particular does not depend on  , \(Y_k\) or \(\varDelta _k\).
, \(Y_k\) or \(\varDelta _k\).
In DFO-GN, we follow BOBYQA and replace these geometry-checking and improvement algorithms (which are called in the safety and model-improvement phases of Algorithm 1) with simplified calculations. Firstly, instead of checking for the \(\varLambda \)-poisedness of \(Y_k\), we instead check if all interpolation points are within some distance of  , typically a multiple of \(\varDelta _k\). If any point is sufficiently far from
, typically a multiple of \(\varDelta _k\). If any point is sufficiently far from  , the geometry of \(Y_k\) is improved by selecting the point
, the geometry of \(Y_k\) is improved by selecting the point  furthest from
furthest from  , and moving it to
, and moving it to  satisfying (4.1). That is, we effectively perform one iteration of the full geometry-improving procedure.
satisfying (4.1). That is, we effectively perform one iteration of the full geometry-improving procedure.
4.2 Model updating
In Algorithm 1, we only update \(Y_{k+1}\), and hence  and \(m_k\), on successful steps. However, in our implementation, we always try to incorporate new information when it becomes available, and so we update
and \(m_k\), on successful steps. However, in our implementation, we always try to incorporate new information when it becomes available, and so we update  on all iterations except when the safety phase is called (since in the safety phase we never evaluate
on all iterations except when the safety phase is called (since in the safety phase we never evaluate  ).
).
Regardless of how often we update the model, we need some criterion for selecting the point  to replace with
to replace with  . There are three common reasons for choosing a particular point to remove from the interpolation set:
. There are three common reasons for choosing a particular point to remove from the interpolation set:
- Furthest Point::
-
It is the furthest away from
 (or
(or  );
); - Optimal \(\varLambda \)-poisedness::
-
Replacing it with
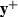 would give the maximum improvement in the \(\varLambda \)-poisedness of \(Y_k\). That is, choose the t for which
would give the maximum improvement in the \(\varLambda \)-poisedness of \(Y_k\). That is, choose the t for which  is maximized;
is maximized; - Stable Update::
-
Replacing it with
 would induce the most stable update to the interpolation system (2.4). As introduced by Powell [27] for quadratic models, moving
would induce the most stable update to the interpolation system (2.4). As introduced by Powell [27] for quadratic models, moving  to
to  induces a low-rank update of the matrix \(W \rightarrow W_{new}\) in the interpolation system, here (2.4). From the Sherman-Morrison-Woodbury formula, this induces a low-rank update of \(H=W^{-1}\), which has the form $$\begin{aligned} H_{new} \leftarrow H + \frac{1}{\sigma _t}\left[ A_t B_t^{\top }\right] , \end{aligned}$$(4.2)
induces a low-rank update of the matrix \(W \rightarrow W_{new}\) in the interpolation system, here (2.4). From the Sherman-Morrison-Woodbury formula, this induces a low-rank update of \(H=W^{-1}\), which has the form $$\begin{aligned} H_{new} \leftarrow H + \frac{1}{\sigma _t}\left[ A_t B_t^{\top }\right] , \end{aligned}$$(4.2)for some \(\sigma _t\ne 0\) and low rank \(A_t B_t^{\top }\). Under this measure, we would want to replace a point in the interpolation set when the resulting \(|\sigma _t|\) is maximal; i.e. the update (4.2) is ‘stable’. In [27], it is shown that for underdetermined quadratic interpolation,
 .
.
Two approaches for selecting  combine two of these reasons into a single criterion. Firstly in BOBYQA, the point t is chosen by combining the ‘furthest point’ and ‘stable update’ measures:
combine two of these reasons into a single criterion. Firstly in BOBYQA, the point t is chosen by combining the ‘furthest point’ and ‘stable update’ measures:

Alternatively, Scheinberg and Toint [31] combine the ‘furthest point’ and ‘optimal \(\varLambda \)-poisedness’ measures:

In DFO-GN, we use the BOBYQA criterion (4.3). However, as we now show, in DFO-GN, the two measures ‘optimal \(\varLambda \)-poisedness’ and ‘stable update’ coincide, meaning our framework allows a unification of the perspectives from [29] and [31], rather than having the indirect relationship via the bound  .
.
To this end, define W as the matrix in (2.4), and let \(H :=W^{-1}\). The Lagrange polynomials for \(Y_k\) can then be found by applying the interpolation conditions (2.9). That is, we have

where  solves
solves

where  is the usual coordinate vector in \({\mathbb {R}}^n\) and
is the usual coordinate vector in \({\mathbb {R}}^n\) and  . This gives us the relations
. This gives us the relations

Now, we consider the ‘stable update’ measure. We will update the point  to
to  , which will give us a new matrix \(W_{new}\) with inverse \(H_{new}\). This change induces a rank-1 update from W to \(W_{new}\), given by
, which will give us a new matrix \(W_{new}\) with inverse \(H_{new}\). This change induces a rank-1 update from W to \(W_{new}\), given by

By the Sherman–Morrison formula, this induces a rank-1 update from H to \(H_{new}\), given by

For a general rank-1 update  , the denominator is
, the denominator is  , and so here we have
, and so here we have

and hence  , as expected.
, as expected.
4.3 Termination criteria
The specification in Algorithm 1 does not include any termination criteria. In the implementation of DFO-GN, we use the same termination criteria as DFBOLS [38], namely terminating whenever any of the following are satisfied:
-
Small objective value: since \(f\ge 0\) for least-squares problems, we terminate when
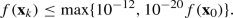 (4.11)
(4.11)For nonzero residual problems (i.e. where
 at the true minimum
at the true minimum  ), it is unlikely that termination will occur by this criterion;
), it is unlikely that termination will occur by this criterion; -
Small trust region: \(\rho _k\), which converges to zero as \(k\rightarrow \infty \) from Lemma 3.10, falls below a user-specified threshold; and
-
Computational budget: a (user-specified) maximum number of evaluations of
 is reached.
is reached.
4.4 Linear algebra implementation details
DFO-GN requires the solution of the interpolation system (2.4) for m (different) right-hand sides at each iteration. We implement this in DFO-GN with a preprocessing step, where we compute an LU factorization of the matrix W, and a solve step, where we use forward/back substitution to solve the system for each right-hand side. The preprocessing step could alternatively be implemented using low-rank updates of \(W^{-1}\) whenever an interpolation point is changed, similar to Powell’s approach [27] for quadratic residual interpolation models. In the case of linear residual models, changing one interpolation point causes a rank-1 update of W and hence of \(W^{-1}\) (see Sect. 4.2), so this approach would give \(W^{-1}\) with \({\mathcal {O}}(n^2)\) cost per iteration, as opposed to the \({\mathcal {O}}(n^3)\) per-iteration cost of an LU factorization.
Using either the factorization preprocessing step or low-rank updates, solving (2.4) with m right-hand sides gives a per-iteration cost for the solve step of \({\mathcal {O}}(mn^2)\). In nonlinear least-squares problems, we have \(m\ge n\), so this cost in general, dominates the preprocessing cost, regardless of the approach used. We chose the factorization approach in DFO-GN because of its simplicity.
By contrast, for underdetermined quadratic residual models with \(p={\mathcal {O}}(n)\) interpolation points (e.g. \(n+2\) or \(2n+1\)), the resulting linear system has size \(p+n+1\). This means that the preprocessing cost is \({\mathcal {O}}((p+n)^3)\) for the factorization approach or \({\mathcal {O}}((p+n)^2)\) for the low-rank update approach, and the solve step has cost \({\mathcal {O}}(m(p+n)^2)\). As a result, if m is not too large compared to n, a factorization-based approach would give a worse per-iteration cost than the low-rank update approach, so there is a benefit to using low-rank update methods. The software DFBOLS [38] uses quadratic models with the low-rank update approach.
4.5 Other implementation differences
Addition of bound constraints Here, we solve (2.1) subject to  for given bounds
for given bounds  . This is allowed in the implementation of DFO-GN as it is important to practical applications. This requires no change to the logic as specified in Algorithm 1, but does require the addition of the same bound constraints in the algorithms for the trust region subproblem (2.6) and calculating geometry-improving steps (4.1). For the trust-region subproblem, we use the routine from DFBOLS, which is itself a slight modification of the routine from BOBYQA (which was specifically designed to produce feasible iterates in the presence of bound constraints). Calculating geometry-improving steps (4.1) is easier, since the Lagrange polynomials are linear rather than quadratic, and so we need to maximize a linear objective subject to Euclidean ball and bound constraints. We use our own routine for this which handles the bound constraints via an active set method; see [4] for full details.
. This is allowed in the implementation of DFO-GN as it is important to practical applications. This requires no change to the logic as specified in Algorithm 1, but does require the addition of the same bound constraints in the algorithms for the trust region subproblem (2.6) and calculating geometry-improving steps (4.1). For the trust-region subproblem, we use the routine from DFBOLS, which is itself a slight modification of the routine from BOBYQA (which was specifically designed to produce feasible iterates in the presence of bound constraints). Calculating geometry-improving steps (4.1) is easier, since the Lagrange polynomials are linear rather than quadratic, and so we need to maximize a linear objective subject to Euclidean ball and bound constraints. We use our own routine for this which handles the bound constraints via an active set method; see [4] for full details.
Other differences The following changes, which are from BOBYQA, are present in the implementation of DFO-GN:
-
We accept any step (i.e. set
 ) where we see an objective reduction—that is, when \(R_k>0\). In fact, we always update
) where we see an objective reduction—that is, when \(R_k>0\). In fact, we always update  to be the best value found so far, even if that point came from a geometry-improving phase rather than a trust region step;
to be the best value found so far, even if that point came from a geometry-improving phase rather than a trust region step; -
The reduction of \(\rho _k\) in an unsuccessful step (line 22) only occurs when \(R_k<0\);
-
Since we update the model on every iteration, we only reduce \(\rho _k\) after 3 consecutive unsuccessful iterations; i.e. we only reduce \(\rho _k\) when \(\varDelta _k\) is small and after the model has been updated several times (reducing the likelihood of the unsuccessful steps being from a bad interpolating set);
-
The method for reducing \(\rho _k\) is usually given by \(\rho _{k+1}=\alpha _1\rho _k\), but it changed when \(\rho _k\) approaches \(\rho _{end}\):
$$\begin{aligned} \rho _{k+1} = {\left\{ \begin{array}{ll} \alpha _1 \rho _k, &{}\quad \text {if }\rho _k > 250\rho _{end}, \\ \sqrt{\rho _k \rho _{end}}, &{}\quad \text {if }16\rho _{end} < \rho _k \le 250 \rho _{end}, \\ \rho _{end}, &{}\quad \text {if }\rho _k \le 16 \rho _{end}. \end{array}\right. } \end{aligned}$$(4.12) -
In some calls of the safety phase, we only reduce \(\rho _k\) and \(\varDelta _k\), without improving the geometry of \(Y_k\).
4.6 Comparison to DFBOLS and POUNDERS
As has been discussed at length, there are many similarities between DFO-GN and DFBOLS from Zhang et al. [38]. The theoretical algorithm described in [38] (called DFLS) allows linear residual models in principle, and its convergence theory covers this case. However, the implementation of this algorithm, DFBOLS, does not, strictly speaking, allow linear residual models; instead, it either uses underdetermined or fully quadratic models for each \(r_i\), with between \(n+2\) and \((n+1)(n+2)/2\) interpolation points. Furthermore, there are no numerical results showing how linear residual models, or models with \(n+2\) points, perform compared to (underdetermined or fully) quadratic residual models.
Aside from this, there are several respects in which DFO-GN is simpler than DFLS/DFBOLS:
-
The use of linear models for each residual (2.1) means we require only \(n+1\) interpolation points, as opposed to between \(n+2\) and \((n+1)(n+2)/2\) points needed by DFBOLS. This results in both a larger interpolation system compared than (2.4) and a larger startup cost (where an initial \(Y_0\) of the correct size is constructed, and
 evaluated at each of these points);
evaluated at each of these points); -
As a result of using linear residual models, there is no ambiguity in how to construct the full model \(m_k\) (2.5). In DFLS and DFBOLS, simply taking a sum of squares of each residual’s model gives a quartic. The authors drop the cubic and quartic terms, and choose the quadratic term from one of three possibilities [38, eqn. (2.4)], depending on
 and
and  . This requires the introduction of three new algorithm parameters, each of which may require calibration; and
. This requires the introduction of three new algorithm parameters, each of which may require calibration; and -
DFO-GN’s method for choosing a point to replace when doing model updating, as discussed in Sect. 4.2, yields a unification of the geometric (‘optimal \(\varLambda \)-poisedness’) and algebraic (‘stable update’) perspectives on this update. In DFBOLS, the connection exists but is less direct, as it uses the same method as BOBYQA (4.3) with
 . As discussed in [29], this bound may sometimes be violated as a result of rounding errors, and thus requires an extra geometry-improving routine to ‘rescue’ the algorithm from this problem. DFO-GN does not need or have this routine.
. As discussed in [29], this bound may sometimes be violated as a result of rounding errors, and thus requires an extra geometry-improving routine to ‘rescue’ the algorithm from this problem. DFO-GN does not need or have this routine.
By comparison, the first bullet point above does not apply to POUNDERS [33], which allows linear models initially, and at each iteration constructs models using \(n+1\le p\le p_{max}\) points, where \(p_{max}\in [n+2,(n+1)(n+2)/2]\) is a user input and p is chosen dynamically each time by selecting points from the full history of iteratesFootnote 9 using the method from [35]. The method of model construction is to use underdetermined quadratic residual models (with minimal change to the model Hessian), and so while linear models are used initially, as soon as \(p>n+1\) for some iteration, quadratic residual models are used in all subsequent iterations. The second point above, however, does not apply, as POUNDERS uses a model for the full objective which is equivalent to a full quadratic approximation (i.e. including all available second-order information). Similarly to existing literature for DFBOLS [38], no numerical results for using only linear residual models in POUNDERS are available; in fact, we are not aware of any existing work showing extensive numerical results or comparisons for POUNDERS.
5 Numerical results
5.1 Solvers tested
In addition to DFO-GN,Footnote 10 we tested the following solvers:
-
DFBOLS, the Fortran implementation from [38], provided by H. ZhangFootnote 11;
-
Py-DFBOLS, our own implementation of DFBOLS, designed to be as similar to DFO-GN in structure as possible. In particular, it is implemented in Python and uses the factorization approach to solving the interpolation system (see Sect. 4.4). As a result, comparing the runtime of DFO-GN with Py-DFBOLS represents a like-for-like test of algorithm speed;
-
BOBYQA [29], a general-objective DFO solver implemented in Fortran by Powell, available from [39]; and,
-
POUNDERS [33], another least-squares DFO code which uses adaptive interpolation models for each residual (see ‘Relevant existing literature’ in Sect. 1 for details), and is incorporated into PETSc. Testing was performed using the Python package petsc4py 3.10.1 and the default setting of using at most \(p_{max}=2n+1\) interpolation points at each iteration.
DFO-GN, Py-DFBOLS and POUNDERS all used Python 3.5.2 with NumPy 1.12.1 and SciPy 1.0.1. The parameter values used for DFO-GN are: \(\varDelta _{max}=10^{10}\), \(\gamma _{dec}=0.5\), \(\gamma _{inc}=2\), \({\overline{\gamma }}_{inc}=4\), \(\eta _1=0.1\), \(\eta _2=0.7\), \(\alpha _1=0.1\), \(\alpha _2=0.5\), \(\omega _S=0.1\) and \(\gamma _S=0.5\). For all solvers, we use an initial trust region radius of  and final trust region radius \(\rho _{end}=10^{-10}\) where possible,Footnote 12 to avoid this being the termination condition as often as possible.
and final trust region radius \(\rho _{end}=10^{-10}\) where possible,Footnote 12 to avoid this being the termination condition as often as possible.
We tested BOBYQA and (Py-)DFBOLS with \(n+2\), \(2n+1\) and \((n+1)(n+2)/2\) interpolation points. All these solvers use quadratic interpolation models, and do not allow the use of \(n+1\) interpolation points. Here, we show the \(n+2\) and \(2n+1\) cases for DFBOLS and the \((n+1)(n+2)/2\) case for Py-DFBOLS. These were chosen because Py-DFBOLS performs very similarly to DFBOLS in the case of \(n+2\) and \(2n+1\) points, and outperforms DFBOLS in the \((n+1)(n+2)/2\) case. Similarly, we show the best-performing \(2n+1\) and \((n+1)(n+2)/2\) cases for BOBYQA.
5.2 Test problems and methodology
We tested the solvers on the test suite from Moré and Wild [20], a collection of 53 unconstrained nonlinear least-squares problems with dimension \(2\le n\le 12\) and \(2\le m \le 65\). For each problem, we optionally allowed evaluations of the residuals \(r_i\) to have stochastic noise. Specifically, we allowed the following noise models:
-
Smooth (noiseless) function evaluations;
-
Multiplicative unbiased Gaussian noise: we evaluate
 , where \(\epsilon \sim N(0,\sigma ^2)\) i.i.d. for each i and
, where \(\epsilon \sim N(0,\sigma ^2)\) i.i.d. for each i and  ;
; -
Additive unbiased Gaussian noise: we evaluate
 , where \(\epsilon \sim N(0,\sigma ^2)\) i.i.d. for each i and
, where \(\epsilon \sim N(0,\sigma ^2)\) i.i.d. for each i and  ; and
; and -
Additive \(\chi ^2\) noise: we evaluate
 , where \(\epsilon \sim N(0,\sigma ^2)\) i.i.d. for each i and
, where \(\epsilon \sim N(0,\sigma ^2)\) i.i.d. for each i and  .
.
To compare solvers, we use data and performance profiles [20]. First, for each solver \({\mathcal {S}}\), each problem p and for an accuracy level \(\tau \in (0,1)\), we determine the number of function evaluations \(N_p({\mathcal {S}};\tau )\) required for a problem to be ‘solved’:

where \(f^*\) is an estimate of the true minimumFootnote 13 . A full list of the values used is provided in Table 2 in Appendix C. We define \(N_p({\mathcal {S}}; \tau )=\infty \) if this was not achieved in the maximum computational budget allowed.
. A full list of the values used is provided in Table 2 in Appendix C. We define \(N_p({\mathcal {S}}; \tau )=\infty \) if this was not achieved in the maximum computational budget allowed.
We can then compare solvers by looking at the proportion of test problems solved for a given computational budget. For data profiles, we normalize the computational effort by problem dimension, and plot (for solver \({\mathcal {S}}\), accuracy level \(\tau \in (0,1)\) and problem suite \({\mathcal {P}}\))
where \(N_g\) is the maximum computational budget, measured in simplex gradients (i.e. \(N_g(n_p+1)\) objective evaluations are allowed for problem p).
For performance profiles, we normalize the computational effort by the minimum effort needed by any solver (i.e. by problem difficulty). That is, we plot
where \(N_p^*(\tau ) :=\min _{{\mathcal {S}}} N_p({\mathcal {S}};\tau )\) is the minimum budget required by any solver.
Profiles for noisy problems In the case of noisy problems, we ran each solver on 10 instances of each problem (i.e. independent realizations of the random noise in objective evaluations). For the data profiles, we consider each problem instance as a separate problem to be ‘solved’; i.e. for the Moré & Wild test set, we plot the proportion of the 530 problem instances solved within a given computational budget. For performance profiles, we do the same (i.e. show a proportion of 530 problem instances), and take \(N_p^*(\tau )\) in (5.3) to be the minimum budget required any solver on any instance of problem p.
5.3 Test results
For our testing, we used a budget of \(N_g=200\) gradients (i.e. \(200(n+1)\) objective evaluations) for each problem, noise level \(\sigma =10^{-2}\), and took 10 runs of each solver.Footnote 14 Most results use an accuracy level of \(\tau =10^{-5}\) in (5.1).
Low accuracy setting Firstly, Fig. 1 shows two performance profiles under the low accuracy requirement \(\tau =10^{-1}\). Here we see an important benefit of DFO-GN and POUNDERS compared to BOBYQA and DFBOLS—allowing a smaller interpolation set means that they can begin the main iteration and make progress sooner. This is reflected in Fig. 1, where DFO-GN and POUNDERS are the fastest solvers more frequently than the others, both with smooth and noisy objective evaluations. However, the performance of POUNDERS is less strong than DFO-GN for larger performance ratios (i.e. \(\alpha \ge 2\) in (5.3)). In line with the results from [38], BOBYQA does not perform as well as POUNDERS, DFBOLS or DFO-GN, as it does not exploit the least-squares problem structure.
The low accuracy requirement often corresponds in practice to the typical case when the objective/residual evaluations are very expensive, more so than the linear algebra and storage costs. The limiting factor then is the (small) evaluation budget, and hence we generally expect objective improvement rather than accurate optimization from the solver. We can also report that DFO-GN was successfully applied in the expensive evaluations regime in the context of a practical energy application [2].
High accuracy setting Next, Fig. 2 shows results for accuracy \(\tau =10^{-5}\) and smooth objective evaluations. Note that our simplification from quadratic to linear residual models has not led to a loss of performance for obtaining high accuracy solutions, and produces essentially identical long-budget performance. At this level, the advantage from the smaller startup cost is no longer seen, but particularly in the performance profile, we can still see the substantially higher startup cost of using \((n+1)(n+2)/2\) interpolation points.
Comparison of DFO-GN with BOBYQA, DFBOLS and POUNDERS for objectives with multiplicative Gaussian, additive Gaussian and additive \(\chi ^2\) noise with \(\sigma =10^{-2}\), to accuracy \(\tau =10^{-5}\). For the BOBYQA and DFBOLS runs, \(n+2\), \(2n+1\) and \({\mathcal {O}}(n^2)=(n+1)(n+2)/2\) are the number of interpolation points
Similarly, Fig. 3 shows the same plots but for noisy problems (multiplicative Gaussian, additive Gaussian and additive \(\chi ^2\) respectively). Here, DFO-GN suffers a small performance penalty (of approximately 5–10%) compared to DFBOLS, particularly when using \(2n+1\) and \((n+1)(n+2)/2\) interpolation points, suggesting that the extra curvature and evaluation information in DFBOLS has some benefit for noisy problems. Also, the performance penalty is larger in the case of additive noise than multiplicative, and here there is also a similar performance penalty compared to POUNDERS. Note that additive noise makes all our test problems nonzero residual (i.e.  for the true minimum
for the true minimum  ); however in the next section we show that this is not a key driver of this differential.
); however in the next section we show that this is not a key driver of this differential.
Note also that, although BOBYQA suffers a substantial performance penalty when moving from smooth to noisy problems, this penalty (compared to DFO-GN and DFBOLS) is much less for additive \(\chi ^2\) noise. This is likely because this noise model makes each residual function more complicated by taking square roots, but the change to the full objective is relatively benign—simply adding \(\chi ^2\) random variables.
Nonzero residual problems We saw above that DFO-GN suffered a higher—but still small—loss of performance, compared to DFBOLS and POUNDERS, for problems with additive noise. To ascertain if this is because Gauss–Newton methods are known to have slower asymptotic convergence rates for nonzero residual problems [21], we extract the performance of the nonzero residual problems only from the test set results we already presented; Fig. 4 shows the resulting performance profiles for accuracy \(\tau =10^{-5}\), for smooth objectives and multiplicative Gaussian noise (\(\sigma =10^{-2}\)). For multiplicative and additive Gaussian noise, we see for all solvers a worse performance on nonzero residual problems (compared to all problems). However, in all cases except additive \(\chi ^2\) noise, DFO-GN performs similarly well against DFBOLS and POUNDERS compared to looking at all problems.
Conclusions to evaluation comparisons The numerical results in this section show that DFO-GN performs comparably to DFBOLS and POUNDERS in terms of evaluation counts, and outperforms BOBYQA, in both smooth and noisy settings, and for low and high accuracy. DFO-GN exhibits a slight performance loss compared to DFBOLS and POUNDERS for additive noisy problems. We may explain the similar performance of DFO-GN to DFBOLS and POUNDERS, despite their use of higher order models, as being due to the general effectiveness of Gauss–Newton-like frameworks for nonlinear least-squares, especially for zero-residual problems; and furthermore, by the usual remit of DFO algorithms in which the asymptotic regimes are not or cannot really be observed or targeted by the accuracy at which the problems are solved.
We note that we also tested other noise models—such as multiplicative uniform noise and also biased variants of the Gaussian noise; all these performed either better (such as in the case of uniform noise) or essentially indistinguishable to the results already presented above. We also tried other noise variance levels, smaller than \(\sigma =10^{-2}\), for which the performance of both DFO-GN and DFBOLS solvers vary similarly/comparably. Though an accuracy level \(\tau =10^{-5}\) is common and considered reasonably high in DFO, to ensure that our results are robust, we also performed the same tests for higher accuracy levels \(\tau \in \{10^{-7},10^{-9},10^{-11}\}\). The resulting profiles are given in Appendix F of the extended technical report [4] of this paper. For smooth problems, DFO-GN is still able to solve essentially the same proportion of problems as (Py-)DFBOLS. For noisy problems, the results are more mixed: overall, DFO-GN does slightly worse for Gaussian noise, but slightly better for \(\chi ^2\) noise. These results are the same when looking at all problems, or just nonzero residual problems. This reinforces our previous conclusions, and gives us confidence that a Gauss–Newton framework for DFO is a suitable choice, and is robust to the level of accuracy required for a given problem.
5.4 Runtime comparison
The use of linear models in DFO-GN also leads to a reduced linear algebra cost. As described in Sect. 4.4, the interpolation system for DFO-GN is of size n, compared to (Py-)DFBOLS, where the system is of size \(p+n+1\) for \(p\ge n+2\) interpolation points; i.e. the (Py-)DFBOLS interpolation system is at least twice the size of the DFO-GN system. Depending on which preprocessing step is used (factorization in Py-DFBOLS or low-rank updates in DFBOLS) and the size of m, we would therefore expect the computational cost of solving the (Py-)DFBOLS system to be at least 4–8 times larger that of DFO-GN (depending on whether the preprocessing or the solve step dominates the cost). To verify this, in this section we compare the runtime of DFO-GN with Py-DFBOLS. Since DFBOLS is implemented in Fortran, a runtime comparison against the Python implementation of DFO-GN will not produce meaningful results. As Py-DFBOLS uses the more expensive factorization-based preprocessing step, we would expect the performance penalty to be nearer the upper end of the 4–8 times range (as a minority of the Moré & Wild test problems have \(m\ge p+n\)).
The wall time required by each solver to run the above testing (with a budget of \(200(n+1)\) objective evaluations) on a Lenovo ThinkCentre M900 (with one 64-bit Intel i5 processor, 8GB of RAM), is shown in Table 1 for both smooth and noisy evaluations. We find that DFO-GN is 7–8 times faster than Py-DFBOLS with \(n+2\) points, 13–23 times faster than Py-DFBOLS with \(2n+1\) points, and 59–444 times faster than Py-DFBOLS with \((n+1)(n+2)/2\) points. In all cases, this is a substantial improvement, particularly given the small difference in performance (measured in function evaluations) between DFO-GN and (Py-)DFBOLS described in Sect. 5.3.
In Table 1, we also show the total number of objective evaluations required by each solver (summed over all instances of all problems). We see that DFO-GN uses slightly more evaluations than Py-DFBOLS for smooth problems, and fewer evaluations (in some cases substantially so) for noisy problems. Firstly, the fact that this does not correlate with runtime indicates that objective evaluation cost is not affecting the runtime results. Secondly, since Sect. 5.3 shows that DFO-GN and (Py-)DFBOLS require a similar number of evaluations to achieve a given accuracy level, this is perhaps evidence that there is scope to implementing more sophisticated termination criteria in both solvers.
We recall again our earlier comment that a reduced runtime due to linear algebra is less important/dominant when objective evaluations are very expensive; see Fig. 1 and associated comments.
5.5 Scalability features
We saw in Sect. 5.4 that DFO-GN runs faster due to the lower cost of solving the interpolation linear system. Another important benefit is that storing the interpolation models for each residual requires only \({\mathcal {O}}(mn)\) memory, rather than \({\mathcal {O}}(mn^2)\) for quadratic models. These two observations together suggest that DFO-GN should scale to large problems better than DFBOLS—in this section we demonstrate this. We consider Problem 29 from Moré, Garbow & Hillstrom [19] (which is Problem 33 (integreq) in the CUTEst set in Table 3).
This is a zero-residual least-squares problem with \(m=n\) variables for solving a one-dimensional integral equation, using an n-point discretization of (0, 1). We compare DFO-GN and DFBOLS with \(n+2\) interpolation points, as it has the smallest memory usage and runtime of all possible values.
In Fig. 5 we compare the per-iteration runtime and peak memory usage of DFBOLS and DFO-GN as n increases. Note that we are comparing DFO-GN (implemented in Python) against DFBOLS (implemented in Fortran) rather than Py-DFBOLS (as used in Sect. 5.4), to put ourselves at a substantial disadvantage. We see that for small n, DFBOLS has significantly lower runtime and memory requirements than DFO-GN (which is unsurprising, since it is implemented in Fortran rather than Python). However, as expected, both the runtime and memory usage increases much faster for DFBOLS than for DFO-GN as n is increased. For \(n>1200\), DFBOLS exceeds the memory capacity of the system. At this point, it has to store data on disk, and as a result the runtime increases very quickly. DFO-GN does not suffer from this issue, and can continue solving problems quickly for substantially larger n. For instance, DFO-GN solves the \(n=2500\) problem over 2.5 times faster per iteration than DFBOLS solves the much smaller \(n=1400\) problem.
Similarly to before, it is important to gain an understanding of whether this improved scalability comes at the cost of performance. To assess this, we consider a set of 60 medium-sized problems (\(25\le n\le 120\) and \(25\le m \le 400\), with \(n\approx 100\) for most problems) from the CUTEst test set [13]. The full list of problems is given in Table 3 in Appendix C. For these problems, we compare DFO-GN with DFBOLS using a smaller budget of \(50(n+1)\) evaluations, commensurate with the greater cost of objective evaluation. Given this small budget, we only test DFBOLS with \(n+2\) and \(2n+1\) interpolation points; using \((n+1)(n+2)/2\) interpolation points would mean in most cases the full budget is entirely used building the initial sample set.
In Fig. 6, we show data and performance profiles for accuracy \(\tau =10^{-5}\). As before, we see that DFO-GN has very similar performance to DFBOLS, and although we have gained improved scalability, we have not lost in terms of performance on medium-sized test problems.
6 Concluding remarks
It is well-known that, for nonlinear least-squares problems, using only linear models for each residual is sufficient to approximate the objective well, especially for zero-residual problems. This forms the basis of the derivative-based Gauss–Newton and Levenberg–Marquardt methods, and has motivated our publicly-availableFootnote 15 derivative-free, model-based trust-region variant here, called DFO-GN. This method is based on the framework from [38], which in principle allows linear, or very close to linear, residual models, but numerically it only assesses the performance of partially or fully quadratic residual models.
We extend the theoretical results of [38] to include that the whole sequence, not just a subsequence, of the gradients at the iterates converges to zero, as well as a worst-case complexity result. We also present the first numerical tests of linear residual models in a DFO context, and we show that DFO-GN reduces both the computational cost of solving the interpolation problem (leading to a runtime reduction of at least a factor of 7) and the memory cost of storing the models (from \({\mathcal {O}}(mn^2)\) to \({\mathcal {O}}(mn)\)). These savings result in a substantially faster runtime and improved scalability of DFO-GN compared to DFBOLS, the implementation from [38] which uses (possibly significantly) underdetermined quadratic residual models. Furthermore, the simpler local models do not adversely affect the algorithm’s performance numerically, in terms of evaluation counts: DFO-GN performs as well as DFBOLS and POUNDERS, the implementation from [33], on smooth test problems from the Moré & Wild and CUTEst collections. When the objective has noise, DFO-GN suffers a small performance penalty compared to DFBOLS and POUNDERS, which is larger for additive than multiplicative noise, but not when considering only nonzero residual problems (compared to all problems). Nonetheless, this, together with the substantial improvements in runtime and scalability, make DFO-GN an appealing choice for both zero and nonzero residuals, and in the presence of noise.
We delegate to future work showing a local quadratic rate of convergence for DFO-GN when applied to nondegenerate zero-residual problems, and generally improving the performance of DFO methods in the presence of noise.
Notes
This implies that the evaluation cost is then \(n+1\) evaluations of each residual for the initialization, and \({\mathcal {O}}(1)\) such evaluations on subsequent iterations.
We could have formulated a linear system to solve for the constant term in (2.2) as well as \(J_k\), but this system becomes poorly conditioned as the algorithm progresses and the points \(Y_k\) get closer together.
The more common approach in the criticality phase (e.g. [9, 12, 38]) is to use an extra parameter \(0<\beta <\mu \) and floor \(\varDelta _k\) at
 , maintaining full linearity with extra assumptions on \(\kappa _{ef}\) and \(\kappa _{eg}\) [8, Lemma 3.2], and requiring all fully linear models have Lipschitz continuous gradient with uniformly bounded Lipschitz constant.
, maintaining full linearity with extra assumptions on \(\kappa _{ef}\) and \(\kappa _{eg}\) [8, Lemma 3.2], and requiring all fully linear models have Lipschitz continuous gradient with uniformly bounded Lipschitz constant.Note that the criticality and safety phases have similar aims, namely, to keep the approximate gradient and the step proportional to \(\varDelta _k\). However, showing global convergence/complexity without a criticality step is unprecedented in the literature, and left for future work.
Note that the analysis in [15] bounds the number of outer iterations of Algorithm 1; i.e. excluding \({\mathcal {C}}^M_{i_{\epsilon }}\) and \({\mathcal {C}}^U_{i_{\epsilon }}\). Instead, they prove that while
 , the criticality phase requires at most \(|\log \epsilon |\) iterations. Thus their bound on the number of objective evaluations is a factor \(|\log \epsilon |\) larger than in [12] and than here.
, the criticality phase requires at most \(|\log \epsilon |\) iterations. Thus their bound on the number of objective evaluations is a factor \(|\log \epsilon |\) larger than in [12] and than here.For second-order methods, the fully quadratic bound is \(\kappa _d={\mathcal {O}}(nC)\).
POUNDERS can also choose from a set of points where the user knows the objective value a priori, an optional input.
Version 1.0, available from https://github.com/numericalalgorithmsgroup/dfogn.
Private correspondence, May 2015.
POUNDERS does not have this as a user input. Instead we set all gradient tolerances to zero.
Note that in [20], and subsequent other papers such as [38], the value \(f^*\) is usually taken to be the smallest objective value achieved by any of the solvers under consideration within a fixed budget. The main motivation in [20] for this choice is for when f is expensive, and so we have small computational budgets and it is possible that no solver converges. In our setting, this is not the case, so we use our (stronger) choice of \(f^*\), which comes from [19] or the results of running these and other (derivative-based) solvers.
Scheduled using [32].
References
Aoki, Y., Hayami, B., De Sterck, H., Konagaya, A.: Cluster Newton method for sampling multiple solutions of underdetermined inverse problems: application to a parameter identification problem in pharmacokinetics. SIAM J. Sci. Comput. 36(1), B14–B44 (2014)
Arter, W., Osojnik, A., Cartis, C., Madho, G., Jones, C., Tobias, S.: Data assimilation approach to analysing systems of ordinary differential equations. In: 2018 IEEE International Symposium on Circuits and Systems (ISCAS) (2018)
Bergou, E., Gratton, S., Vicente, L.N.: Levenberg–Marquardt methods based on probabilistic gradient models and inexact subproblem solution, with application to data assimilation. SIAM/ASA J. Uncertain. Quantif. 4(1), 924–951 (2016)
Cartis, C., Roberts, L.: A Derivative-Free Gauss–Newton Method. Tech. rep., University of Oxford, Mathematical Institute (2017). Available on Optimization Online
Conn, A.R., Gould, N.I.M., Toint, P.L.: Trust-Region Methods. MPS-SIAM Series on Optimization. MPS/SIAM, Philadelphia (2000)
Conn, A.R., Scheinberg, K., Toint, P.L.: Recent progress in unconstrained nonlinear optimization without derivatives. Math. Program. 79, 397–414 (1997)
Conn, A.R., Scheinberg, K., Vicente, L.N.: Geometry of interpolation sets in derivative free optimization. Math. Program. 111(1–2), 141–172 (2007)
Conn, A.R., Scheinberg, K., Vicente, L.N.: Global convergence of general derivative-free trust-region algorithms to first- and second-order critical points. SIAM J. Optim. 20(1), 387–415 (2009)
Conn, A.R., Scheinberg, K., Vicente, L.N.: Introduction to Derivative-Free Optimization, MPS-SIAM Series on Optimization, vol. 8. MPS/SIAM, Philadelphia (2009)
Conn, A.R., Toint, P.L.: An Algorithm using Quadratic Interpolation for Unconstrained Derivative Free Optimization. In: Di Pillo, G., Gianessi, F. (eds.) Nonlinear Optimization and Applications, pp. 27–47. Plenum Publishing, New York (1996)
Custódio, A.L., Scheinberg, K., Vicente, L.N.: Methodologies and Software for Derivative-free Optimization. In: Terlaky, T., Anjos, M.F., Ahmed, S. (eds.) Advances and Trends in Optimization with Engineering Applications, MOS-SIAM Book Series on Optimization. SIAM, Philadelphia (2017)
Garmanjani, R., Júdice, D., Vicente, L.N.: Trust-region methods without using derivatives: worst case complexity and the nonsmooth case. SIAM J. Optim. 26(4), 1987–2011 (2016)
Gould, N.I.M., Orban, D., Toint, P.L.: CUTEst: a constrained and unconstrained testing environment with safe threads for mathematical optimization. Comput. Optim. Appl. 60(3), 545–557 (2015)
Gould, N.I.M., Porcelli, M., Toint, P.L.: Updating the regularization parameter in the adaptive cubic regularization algorithm. Comput. Optim. Appl. 53(1), 1–22 (2012)
Grapiglia, G.N., Yuan, J., Yuan, Yx: A derivative-free trust-region algorithm for composite nonsmooth optimization. Comput. Appl. Math 35(2), 475–499 (2016)
Júdice, D.: Trust-Region Methods without using Derivatives: Worst-Case Complexity and the Non-Smooth Case. Ph.D. thesis, University of Coimbra (2015)
Kolda, T.G., Lewis, R.M., Torczon, V.: Optimization by direct search: new perspectives on some classical and modern methods. SIAM Rev. 45(3), 385–482 (2003)
Lukšan, L.: Hybrid methods for large sparse nonlinear least squares. J. Optim. Theory Appl. 89(3), 575–595 (1996)
Moré, J.J., Garbow, B.S., Hillstrom, K.E.: Testing unconstrained optimization software. ACM Trans. Math. Softw. 7(1), 17–41 (1981)
Moré, J.J., Wild, S.M.: Benchmarking derivative-free optimization algorithms. SIAM J. Optim. 20(1), 172–191 (2009)
Nocedal, J., Wright, S.J.: Numerical Optimization, Springer Series in Operations Research and Financial Engineering., 2nd edn. Springer, New York (2006)
Oeuvray, R., Bierlaire, M.: BOOSTERS: a derivative-free algorithm based on radial basis functions. Int. J. Model. Simul. 29(1), 26–36 (2009)
Powell, M.J.D.: A direct search optimization method that models the objective and constraint functions by linear interpolation. In: S. Gomez, J.P. Hennart (eds.) Adv. Optim. Numer. Anal., pp. 51–67. Kluwer Academic Publishers, Dordrecht (1994)
Powell, M.J.D.: Direct search algorithms for optimization calculations. Acta Numer. 7, 287–336 (1998)
Powell, M.J.D.: UOBYQA: Unconstrained optimization by quadratic approximation. Math. Program. 92(3), 555–582 (2002)
Powell, M.J.D.: On trust region methods for unconstrained minimization without derivatives. Math. Program. 97(3), 605–623 (2003)
Powell, M.J.D.: Least Frobenius norm updating of quadratic models that satisfy interpolation conditions. Math. Program. 100(1), 183–215 (2004)
Powell, M.J.D.: A view of algorithms for optimization without derivatives. Tech. Rep. DAMTP 2007/NA03, University of Cambridge (2007)
Powell, M.J.D.: The BOBYQA algorithm for bound constrained optimization without derivatives. Tech. Rep. DAMTP 2009/NA06, University of Cambridge (2009)
Ralston, M.L., Jennrich, R.I.: Dud, a derivative-free algorithm for nonlinear least squares. Technometrics 20(1), 7–14 (1978)
Scheinberg, K., Toint, P.L.: Self-correcting geometry in model-based algorithms for derivative-free unconstrained optimization. SIAM J. Optim. 20(6), 3512–3532 (2010)
Tange, O.: GNU Parallel: the command-line power tool. ;login USENIX Mag. 36(1), 42–47 (2011)
Wild, S.M.: POUNDERS in TAO: solving derivative-free nonlinear least-squares problems with POUNDERS. In: Adv. Trends Optim. with Eng. Appl., chap. 40, pp. 529–539. SIAM, Philadelphia, PA (2017)
Wild, S.M., Regis, R.G., Shoemaker, C.A.: ORBIT: optimization by radial basis function interpolation in trust-regions. SIAM J. Sci. Comput. 30(6), 3197–3219 (2008)
Wild, S.M., Shoemaker, C.A.: Global convergence of radial basis function trust-region algorithms for derivative-free optimization. SIAM Rev. 55(2), 349–371 (2013)
Winfield, D.: Function minimization by interpolation in a data table. IMA J. Appl. Math. 12(3), 339–347 (1973)
Zhang, H., Conn, A.R.: On the local convergence of a derivative-free algorithm for least-squares minimization. Comput. Optim. Appl. 51(2), 481–507 (2012)
Zhang, H., Conn, A.R., Scheinberg, K.: A derivative-free algorithm for least-squares minimization. SIAM J. Optim. 20(6), 3555–3576 (2010)
Zhang, Z.: Software by Professor M. J. D. Powell. http://mat.uc.pt/~zhang/software.html (2017)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This work was supported by the EPSRC Centre For Doctoral Training in Industrially Focused Mathematical Modelling (EP/L015803/1) in collaboration with the Numerical Algorithms Group Ltd. In compliance with EPSRC’s open access initiative, the data in this paper is available from http://dx.doi.org/10.5287/bodleian:VYPX4K5QR.
Appendices
A Proof of Lemma 3.3
This proof is similar to [38, Lemma 4.3] and [9, Theorems 2.11 and 2.12]; but the precise values of the constants matter, so we include the details here. Define  for convenience. We recall the standard bound [21, Appendix A]
for convenience. We recall the standard bound [21, Appendix A]

From the interpolation conditions (2.3), we have

Using (A.1), we compute for any \(t=1,\ldots ,n\),

Let \({\hat{W}}_k\) be the interpolation matrix of the system (2.4) scaled by \(\varDelta _k^{-1}\). Considering the matrix  , with columns
, with columns  , we have
, we have

and so using the identity \(\Vert {\hat{W}}^{-1}_k\Vert =\Vert {\hat{W}}^{-\top }_k\Vert \), we get

Thus we conclude that for any 

Since \(Y_k\) is \(\varLambda \)-poised in B, we have \(\Vert {\hat{W}}^{-1}_k\Vert ={\mathcal {O}}(\varLambda )\) from [9, Theorem 3.14]. Thus (2.14) holds with \(\kappa _{eg}^r :=L_J \left( 1 + \frac{1}{2}\sqrt{n}C\right) \), where \(C={\mathcal {O}}(\varLambda )\). Next, we prove (2.13) by computing



where we use (2.14) and (A.1). Hence we have (2.13) with \(\kappa _{ef}^r = \kappa _{eg}^r + L_J/2\), as required. Since  is fully linear, we also get from (2.14) the bound
is fully linear, we also get from (2.14) the bound  , so \(\Vert J_k\Vert \) is uniformly bounded for all k. Since \(H_k = J_k^{\top }J_k\), this means that \(\Vert H_k\Vert = \Vert J_k\Vert ^2\) is uniformly bounded for all k. To prove full linearity of \(m_k\), we first compute
, so \(\Vert J_k\Vert \) is uniformly bounded for all k. Since \(H_k = J_k^{\top }J_k\), this means that \(\Vert H_k\Vert = \Vert J_k\Vert ^2\) is uniformly bounded for all k. To prove full linearity of \(m_k\), we first compute



recovering (2.12) with \(\kappa _{eg}=L_{\nabla f} + \kappa _{eg}^r r_{max} + (\kappa _{eg}^r\varDelta _{max}+J_{max})^2\), as required.
Lastly, to show (2.11), we recall the scalar version of (A.1)

We use this and (2.12) to compute




and so we have (2.11) with \(\kappa _{ef} = \kappa _{eg} + L_{\nabla f}/2 + (\kappa _{eg}^r\varDelta _{max} + J_{max})^2/2\). \(\square \)
B Geometry improvement in criticality phase
Here, we describe the geometry-improvement step performed in the criticality phase of Algorithm 1, and prove its convergence. The proof of Lemma B.1 can be derived from that of [9, Lemma 10.5].

We recall from Lemma 3.3 that if \(Y_k^{(i)}\) is \(\varLambda \)-poised in  , then \(m_k^{(i)}\) is fully linear in the sense of Definition 2.3, with associated constants \(\kappa _{ef}\) and \(\kappa _{eg}\) in (2.11) and (2.12) respectively given by (3.3).
, then \(m_k^{(i)}\) is fully linear in the sense of Definition 2.3, with associated constants \(\kappa _{ef}\) and \(\kappa _{eg}\) in (2.11) and (2.12) respectively given by (3.3).
Lemma B.1
Suppose  . Then for any \(\mu >0\) and \(\omega _C\in (0,1)\), Algorithm 2 terminates in finite time with \(Y_k\)\(\varLambda \)-poised in
. Then for any \(\mu >0\) and \(\omega _C\in (0,1)\), Algorithm 2 terminates in finite time with \(Y_k\)\(\varLambda \)-poised in  and
and  for any \(\mu >0\) and \(\omega _C\in (0,1)\). We also have the bound
for any \(\mu >0\) and \(\omega _C\in (0,1)\). We also have the bound
Proof
First, suppose Algorithm 2 terminates on the first iteration. Then \(\varDelta _k=\varDelta _k^{init}\), and the result holds. Otherwise, consider some iteration i where Algorithm 2 does not terminate; that is, where  . Then since \(m_k^{(i)}\) is fully linear in
. Then since \(m_k^{(i)}\) is fully linear in  , we have
, we have

or equivalently \(\displaystyle \omega _C^{i-1} \ge \frac{\epsilon }{(\kappa _{eg}+1/\mu )\varDelta _k^{init}}. \) That is, if termination does not occur on iteration i, we must have
so Algorithm 2 terminates finitely. We also have \(\displaystyle \omega _C^{i-1}\varDelta _k^{init} \ge \frac{\epsilon }{\kappa _{eg}+1/\mu }\), which gives (B.1). \(\square \)
C Test problems
 and \(2f^*\); i.e. excluding the 1 / 2 factor in (2.1)
and \(2f^*\); i.e. excluding the 1 / 2 factor in (2.1) and \(2f^*\), as per Table 2)
and \(2f^*\), as per Table 2)Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Cartis, C., Roberts, L. A derivative-free Gauss–Newton method. Math. Prog. Comp. 11, 631–674 (2019). https://doi.org/10.1007/s12532-019-00161-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12532-019-00161-7
Keywords
- Derivative-free optimization
- Least-squares
- Gauss–Newton method
- Trust region methods
- Worst-case complexity


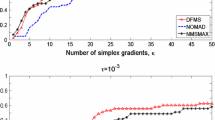


 (i.e.
(i.e. 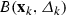 ); and
); and

 (
(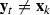 ) for which
) for which  is maximized (c.f. (
is maximized (c.f. ( in
in  , where
, where 
 (or
(or  );
);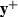 would give the maximum improvement in the
would give the maximum improvement in the  is maximized;
is maximized; would induce the most stable update to the interpolation system (
would induce the most stable update to the interpolation system ( to
to  induces a low-rank update of the matrix
induces a low-rank update of the matrix  .
.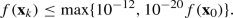
 at the true minimum
at the true minimum  ), it is unlikely that termination will occur by this criterion;
), it is unlikely that termination will occur by this criterion; is reached.
is reached. ) where we see an objective reduction—that is, when
) where we see an objective reduction—that is, when  to be the best value found so far, even if that point came from a geometry-improving phase rather than a trust region step;
to be the best value found so far, even if that point came from a geometry-improving phase rather than a trust region step; evaluated at each of these points);
evaluated at each of these points); and
and  . This requires the introduction of three new algorithm parameters, each of which may require calibration; and
. This requires the introduction of three new algorithm parameters, each of which may require calibration; and . As discussed in [
. As discussed in [ , where
, where  ;
; , where
, where  ; and
; and , where
, where  .
.





 , maintaining full linearity with extra assumptions on
, maintaining full linearity with extra assumptions on  , but we need it to hold on all iterations. However, most of our analysis holds if this assumption is removed—see Remark
, but we need it to hold on all iterations. However, most of our analysis holds if this assumption is removed—see Remark  , the criticality phase requires at most
, the criticality phase requires at most