Introduction

The principle of GNSS (Global Navigation Satellite Systems) positioning based on one-way measurements—satellite signals are registered by receivers. Equation system of four unknowns (three coordinates and one receiver clock error) required the view of at least four satellites every epoch, especially in kinematic positioning. This method is called absolute positioning using a single receiver with pseudoranges, and there is no need of timescales synchronisation. For more precise purposes, phase measurements with the usage of two or more receivers are in use. In that kind of measurements, determination of the GNSS satellite on-board clock corrections is the most important part. Satellite clock corrections are provided via navigation message in real-time or in post-processing (Krawinkel and Schön 2016). Satellite clock correction determination needs continuous observations based on large number of permanent stations (Gong et al. 2013). The biggest network of permanent station is IGS (The International GNSS Service). IGS provides precise GNSS products such as precise ephemeris or stations’ coordinates since 1994 (Beutler et al. 2009). Five-minute sampling clock corrections are available at IGS for many years; 30-s sampling data are available since GPS week 1406 (December 17, 2006) (Gendt 2007) by a four IGS ACs (analysis centres) (Bock et al. 2009). In 2012, the Multi-GNSS EXperiment (MGEX) was initiated (Montenbruck et al. 2013) to prepare the services for new GNSS systems, such as BeiDou or Galileo (Prange et al. 2017a). Since GPS week 1961 (August 6, 2017), MGEX 30-s clock corrections are also available. Products with this interval are provided by three IGS ACs: CODE (Centre for Orbit Determination in Europe) (Prange et al. 2017b), GFZ (Geo Forschungs Zentrum) (Uhlemann et al. 2015) and CNES/CLS (Centre National d’Etudes Spatiales/Collecte Localisation par Satellite) (Loyer et al. 2016). As research shows, clock products provided by different institutions and analysis centres differ insignificantly from each other, but generally, accuracy is at the same level (Ruan et al. 2017). High-rate clock products (< 5 s) are used in 1-Hz and lower measurement intervals, mostly in absolute measurements, e.g. PPP. In this positioning method, the satellite clock error cannot be deleted by differencing observations, and the knowledge of high-quality clock corrections is extremely important (Kouba and Héroux 2001; Lou et al. 2016; Soycan 2011). High-rate PPP measurements are in use in the monitoring of natural and anthropological phenomena such as seismic wave motions (Xu et al. 2013), permanent stations monitoring (Maciuk 2016a; Szombara and Maciuk 2017), landslides control surveys (Şanlıoğlu et al. 2016) and earthquakes observations (Kaloop and Rabah 2016).

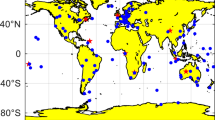
In this work, the author performs the determination of satellite clock error based on high-rate 1-Hz observation data in a 2-h interval window. The processing methodology with basics of atomic clock stability analysis is introduced in the following section. Data from 14 IGS stations located in Europe (Fig. 1) with various types of clocks were selected for the study. Three different types of station reference clocks were applied: internal, external caesium and external h-maser. During the 2-h observation window, only ten GPS satellites were continuously visible for at least 4000 epochs. The short-term stability of satellites was characterised in terms of the Allan deviation (ADEV) by using the method described in the next paragraph. The general purpose was the determination of the impact of the ground reference clock on the accuracy of satellite clocks. Results are presented for each satellite as ADEV for few intervals between 1 and 1000 s.

Fig. 1
figure 1

Distribution of the tracking stations involved in the experiment

Full size image

Clock stability analysis theory

Frequency accuracy refers to consistency from the measured frequency (or calculated rate) and the nominal one and can be defined as:

$$ \sigma =\frac{f_x-{f}_0}{f_0} $$
(1)

where σ is the frequency accuracy, f0 is the nominal frequency and fx is the actual frequency value. Measurement frequency accuracy analysis needs a longer frequency measurement time as far as possible. If frequency measurement time is too short, short-term stability of frequency standard is relatively poor, and random frequency fluctuations will affect the accuracy of measurement error.

Frequency accuracy is calculated by the time difference method, thus can be called the relative frequency deviation as the accuracy of the satellite atomic clock. The atomic clock frequency can be described by the frequency drift rate. The least-squares solution of the frequency drift rate is described as (Zheng et al. 2017):

$$ D=\frac{\sum_{i=1}^N\left({y}_i-\overline{y}\right)\left({t}_i-\overline{t}\right)}{\sum_{i=1}^N{\left({t}_i-\overline{t}\right)}^2} $$
(2)

where D is the frequency drift rate, \( \overline{y} \) is the mean value of relative frequency value yi, ti is the time measure of the relative frequency value and N is the number of samples; the formulas of \( \overline{y} \) and \( \overline{t} \) are:

$$ \overline{y}=\frac{1}{N}\sum \limits_{i=1}^N{y}_i $$
(3)
$$ \overline{t}=\frac{1}{N}\sum \limits_{i=1}^N{t}_i $$
(4)

The Allan deviation or its square (Allan variance) is the most often used method for satellite clock estimation (Allan 1983). If discrete set of time deviations xi as a sequence for the measurable time difference and given nominal spacing between adjacent time difference measurements is τ0, then the average fractional frequency for the ith measurement interval is (Allan 1987):

$$ {\overline{y}}_i^{\tau_0}=\frac{x_{i+1}-{x}_i}{\tau_0} $$
(5)

where τ0 over yi denotes the average over an interval τ0. According to that, the Allan variance generally can be described as a half of the mean square value of the change in frequency error (Petovello and Lachapelle 2000):

$$ {\sigma}_y^2\left(\tau \right)=\frac{1}{2}\left\{{\left(\Delta {\overline{y}}^{\tau}\right)}^2\right\} $$
(6)

where \( \Delta {\overline{y}}^{\tau } \) is the difference in adjacent fractional frequency measurements, each averaged over a time interval τ. If τ0 is the minimum sampling of original data set \( {\overline{y}}_i^{\tau_0} \), then the change of the sampling time to τ = nτ0 by averaging n adjacent values of \( {\overline{y}}_i^{-{\tau}_0} \) to get a new fractional frequency estimate \( {\overline{y}}_i^{\tau } \), with sampling time τ as input to (6). For a finite set of M, values of \( {\overline{y}}_i^{\tau_0} \) for general τ becomes (Allan 1987):

$$ {\sigma}_y^2\left(\tau \right)=\frac{1}{2\left(M-2n+1\right)}\sum \limits_{k=1}^{M-2n+1}{\left({\overline{y}}_{k+n}^{\tau }-{\overline{y}}_k^{\tau}\right)}^2 $$
(7)

where \( {\overline{y}}_{k+n}^{\tau } \) and \( {\overline{y}}_k^{\tau } \) are still adjacent fractional frequencies, each averaged over τ = nτ0, and (Allan 1987).

$$ {\overline{y}}_k^{\tau }=\frac{1}{n}\sum \limits_{i=k}^{k+n-1}{\overline{y}}_i^{\tau_0}=\frac{x_{k-n}-{x}_k}{\tau } $$
(8)

Or, alternatively, (7) may be written as (9):

$$ {\sigma}_y^2\left(\tau \right)=\frac{1}{2{\tau}^2\left(M-2n+1\right)}\sum \limits_{k=1}^{M-2n+1}{\left({x}_{i+2n}-2{x}_{i+n}+{x}_i\right)}^2 $$
(9)

where M = N − 1 is the number of frequency samples, and N is the number of time samples, i = 1 to M + 1:

$$ {x}_{k+1}={\tau}_0\sum \limits_{i=1}^k{\overline{y}}_k^{\tau }+{x}_i $$
(10)

From Equations (9) and (11), we see that \( {\sigma}_y^2\left(\tau \right) \) acts like a second-difference operator, which makes use of overlapping estimate of the expected values of frequency measurements (Allan et al. 1988). The Allan deviation (denoted as σy(τ) or ADEV) versus time interval is usually plotted in a log-log format. It is also known as a two-sample variance and describes clock behaviour as a function of the time between samples of τ size.

GNSS observation models

Precise clock products are extremely important in GNSS positioning. It is extremely important firstly in absolute positioning method called PPP (Precise Point Positioning) demanding high-quality products (Alcay et al. 2012a; Maciuk 2018a). Secondly, in real-time positioning methods (Krzyżek 2015), available ultra-rapid orbit might improve results contrary to the broadcasted orbit (Maciuk 2016b). And finally, clock files are required among other precise clock products in measurements in difficult conditions such as under difficult sky-view conditions (Maciuk 2018b; Alcay et al. 2012b).

Precise clock product accuracy depends on the provider, which leads to slight differences; clock products can diverge by accuracy, availability, update rate and sampling rate (Zheng et al. 2017). The pseudorange (code) and phase observations in GNSS positioning are smudged by various factors. It can be classified into receiver and satellite clock bias, satellite position error, ionosphere and troposphere delays, earth rotation corrections, relativistic and multipath effects and others. Therefore, the above factors have to be eliminated to determine satellite clock bias. Carrier phase observations are much more precise than pseudorange observations; both observations can be expressed as (Bock et al. 2009; Li et al. 2016):

$$ {p}_{fk}^j\left({t}_i\right)={\rho}_k^j\left({t}_i\right)-c\bullet {\delta}^j\left({t}_i\right)+c\bullet {\delta}_k\left({t}_i\right)+{\rho}_{fk, iono}^j\left({t}_i\right)+{\rho}_{k, trop}^j\left({t}_i\right)+c\bullet {b}^j $$
(11)
$$ {\varphi}_{fk}^j\left({t}_i\right)={\rho}_k^j\left({t}_i\right)-c\bullet {\delta}^j\left({t}_i\right)+c\bullet {\delta}_k\left({t}_i\right)-{\rho}_{fk, iono}^j\left({t}_i\right)+{\rho}_{k, trop}^j\left({t}_i\right)+{\lambda}_f\bullet {N}_k^j $$
(12)

where \( {p}_{fk}^j \) is the observed pseudorange; \( {\rho}_k^j \) is the slant distance; δj and δk are satellite and receiver clock corrections, respectively; \( {\rho}_{fk, iono}^j \) and \( {\rho}_{k, trop}^j \) are ionospheric and tropospheric refractions, respectively; bj is the differential clock bias (DCB); c is the speed of light; \( {\varphi}_{fk}^j \) is the observed phase; λf is the wavelength of frequency f and \( {N}_k^j \) is the ambiguity. Comparing code and phase observations, we have the ambiguity term and the opposite sign for ionosphere refraction. The ambiguity term (\( {\lambda}_f\bullet {N}_k^j \)) is eliminated by differences of phase measurements referring to subsequent epochs as:

$$ {\Delta \varphi}_{fk}^j\left({t}_{i+1,i}\right)={\varphi}_{fk}^j\left({t}_{i+1}\right)-{\Delta \varphi}_{fk}^j\left({t}_i\right) $$
(13)

Precise GNSS orbits, ERPs (Earth Rotation Parameters), station coordinates, DCBs and troposphere parameters are used as known; ionosphere impact is eliminated in ionosphere-free LC (linear combination) (Han et al. 2001), so Equations (11) and (12) are expressed as Equations (14) and (15), respectively:

$$ {CP}_k^j\left({t}_i\right)=-c\bullet {\delta}^j\left({t}_i\right)+c\bullet {\delta}_k\left({t}_i\right) $$
(14)
$$ {\varDelta C\varphi}_{fk}^j\left({t}_{i+1,i}\right)=-c\bullet {\Delta \delta}^j\left({t}_{i+1,i}\right)+c\bullet {\Delta \delta}_k\left({t}_{i+1,i}\right) $$
(15)

For the phase-difference processing, the differences between epoch-wise estimated code and receiver corrections are used as a priori values. Differences between subsequent observations epochs are correlated as long as they are connected with at least one ambiguity term (Bock et al. 2009). Clock corrections might be estimated from zero-difference data in two different ways (Dach and Walser 2013). Firstly, by estimating together with other parameters (e.g. coordinate and troposphere) in main normal equations; this method is widely known. The second was as set-up pre-eliminated epoch by epoch. After solving normal equations, resulting parameters are introduced as fixed when epoch parameters are estimated epoch by epoch. In other words, a single solution is set up as a reference for a number of epochs for defined interval (usually 30 s or 300 s). This value might be obtained either from the code measurements or from the external high-accuracy input of clock correction file. This procedure is done separately for each individual satellite and receiver clock. For a particular clock, such combinations could be written as (Zhang et al. 2011):

$$ \left\{\begin{array}{c}\begin{array}{c}-\delta \left({t}_1\right)+\delta \left({t}_2\right)\kern11.5em =\Delta \delta \left({t}_{2,1}\right)\\ {}\kern3.75em -\delta \left({t}_2\right)+\delta \left({t}_3\right)\kern7.75em =\Delta \delta \left({t}_{3,1}\right)\end{array}\\ {}\begin{array}{c}\cdots \\ {}\kern12em -\delta \left({t}_{n-1}\right)+\delta \left({t}_n\right)=\Delta \delta \left({t}_{n,n-1}\right)\end{array}\end{array}\right. $$
(16)

where n is number of epochs, with constrains

$$ \left\{\begin{array}{c}\delta \left({t}_1\right)={\delta}_{fix}\left({t}_1\right)\\ {}\delta \left({t}_n\right)={\delta}_{fix}\left({t}_n\right)\end{array}\right. $$
(17)

For example, if 5-min sampling clock data are in use as input and epoch-differencing is done for 30-s sampling data, the known clock corrections δfix(ti) are introduced with 5-min resolution. In both cases, estimated clock corrections are identical (Dach and Walser 2013). The second approach dramatically reduces the number of parameters in the main normal equations, so it is computationally and efficiently productive compared to the first method.

Experiment description and results

Clock estimations were estimated using zero-difference data epoch by epoch. In elaboration, parameters were calculated for all satellite clocks setting up different types of receiver clock as a reference. A full list of the IGS stations taken into consideration is provided in Table 1.

Table 1 Basic information of the tracking stations involved in the experiment
Full size table

The analysis includes only the reference stations located in Europe belonging to the IGS network and providing 1-Hz observations (Fig. 1). As a reference clock (fixed), three stations were taken with different types of clock: internal (ZIM2), external caesium (GOP6) and external h-maser (WTZR), located in the centre of network. Satellite clocks were calculated with respect to a specific receiver clock. The selection of reference stations was taken both on the clock type and on the localisation in the analysed network.

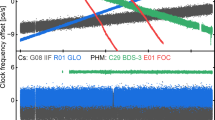
Figure 2 shows ADEV calculated based on CODE’s final 30-s products from 31 December 2017 to 13 January 2018 for averaging intervals of τ ≥ 30 s. Differences between clock-type stability (internal, ZIM2; caesium, GOP6 and h-maser, WTZR) are very clear. In the case of shortest interval (τ = 30 s), discrepancies are evident: 1.9e-11 s for ZIM2 station, 5.9e-12 s for GOP6 and 1.2e-12 s for WTZR. Moving to longer averaging intervals, τ variations between analysed clocks are getting smaller. For each analysed value, the h-maser clock is the most stable, and the internal clock is the least, except the longest analysed τ = 15,360 s. In addition, the h-maser clock characterises by one order of magnitude with better stability than the internal one and by half of one order of magnitude against the caesium one.

Fig. 2
figure 2

Frequency instability of analysed reference stations

Full size image

In this work, 1-Hz data from reference stations presented in Table 1 for 1 January 2018, between 00:00 and 02:00 UTC, were taken. That sort of date gives 7200 observation epochs in the analysed period. For further processing, at least 4096 continuous, singular clock data were taken into consideration. This kind of limitation carries out ten GPS satellites (Table 2). Considered satellites consist of three different types of the newest blocks: IIR, IIR-M and IIF, with three different frequency standards: Rb1, Rb2 and Rb3.

Table 2 Information about satellites (http://www2.unb.ca/gge/Resources/GPSConstellationStatus.txt, https://www.navcen.uscg.gov/?Do=constellationstatus)
Full size table

Figure 3 (Appendix) presents ADEV for each of the three different reference clock solutions of all satellites that fulfil the condition described in the previous paragraph. Selected values are presented in Table 2. As expected, all three reference clock solutions show a different behaviour. For a ZIM2 station (internal clock), satellite clock stability varies between 2.96E-11 s (for τ = 1 s) and 1.16E-12 s (τ = 1024 s). In case of a GOP6 (caesium clock), clock stability varies between 2.09E-11 s (τ = 1 s) and 1.51E-13 s (τ = 1024 s). The most stable was WTZR clock (h-maser clock) with stability from 1.97E-11 s (τ = 1 s) to 5.87E-14 s (τ = 1024 s)

Each analysed case shows that for τ = 1 s, the least stable is G16 satellite clock with instability at 2-3E-11 s level. The ADEV curves for ZIM2 and GOP6 stations are very similar; there are no deviations between each satellite instead of the event explained at the beginning of the paragraph. In the case of the most stable resolution based on WTZR reference clock, G26 and G27 satellite clocks have a clearly visible better ADEV results for τ > 8 s values (Table 3). There is no connection between these pairs of satellites based on the values placed in Table 1—different planes, block and frequency standard.

Table 3 Allan deviation of selected intervals
Full size table

Conclusions

The author presents the stability of satellite clocks based on different reference clock types. 1-Hz GNSS data in 2-h observation interval is analysed using three different reference clocks: internal, caesium and h-maser oscillators. Reference clock stability is analysed in a 2-week period on the basis of 30-s IGS products that show that the h-maser clock stability is better by one order of magnitude than the internal clock and by half of one order of magnitude than the caesium one. The clock parameters are estimated epoch by epoch using a back-substitution steps method described in the text. Research shows a close correlation between the reference clock and the estimated clock stability. Internal oscillator shows close to 1E-12-s stability, caesium one 1.5E-13 s and h-maser 6E-13 s. Studies also show no connection between launch date of satellite, block type or frequency standard and satellite clock stability. These results should be incorporated into future satellite clock determination elaborations for short-term analyses with high interval observations.