A web-based group decision support system for multicriteria ranking problems

Abstract

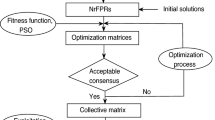
In this paper, we present an implemented, web-based multicriteria group decision support system for solving multicriteria ranking problems by a collaborative group of decision-makers in sequential or parallel coordination mode and in a distributed and asynchronous environment. This system employs an order-based consensus model for collaborative groups that moves from consistency to consensus. The system is based on consensus measures and it has been designed to provide advice to the decision-makers to increase group consensus level while maintaining the individual consistency of each decision-maker. It is based on the use of fuzzy outranking relations to model individual and group preferences. For the exploitation of the models—formulated as a multiobjective optimization problem and solved with a multiobjective evolutionary algorithm—the system generates advice on how decision-makers should change their preferences to reach a ranking of alternatives with a high degree of consistency and consensus.

Appendices

Appendix 1: A procedure for reaching consistency based on multiobjective combinatorial optimization

Let A = {a ₁, a ₂, …, a _m } be the set of decision alternatives or potential actions, and let us consider a fuzzy outranking relationship S ^σ _A defined on A × A; this means that we associate with each ordered pair (a _i , a _j ) ∊ A × A a real number σ(a _i , a _j )(0 ≤ σ(a _i , a _j ) ≤ 1) that reflects the degree of strength of the arguments favoring the crisp outranking a _i S _A a _j .

The exploitation phase transforms the global information included in S ^σ _A into a global ranking of the elements of A (Fodor and Roubens 1994). The main difficulty in the exploitation phase of all outranking methods consists of finding reasonable means of dealing with non-transitivities without losing too much of the content of the original outranking relationship (Leyva and Araoz 2013). In methods based on score functions, non-consistent situations could occur when the prescription is constructed. The most significant situation is the following: suppose that a _i and a _j are two actions such that σ(a _i , a _j ) ≥ λ and σ(a _j , a _i ) ≤ λ − β(β > 0). If λ ≥ c and β ≥ t (c and t representing consensus and threshold levels, respectively, which are usually given by the decision-maker), we should accept that “a _i outranks a _j ” (a _i S ^λ _A a _j ) and that “a _j does not outrank a _i ” $(a_{j} \,\sim\,S_{A}^{\lambda } a_{i} )$. In this case, the global preference model captured in the outranking relationship provides a presumed preference favoring a _i . A score function or other similar method could lead, however, to a final ordering in which a _j is ranked before, giving a pairwise rank reversal effect (Mareschal et al. 2008; Roy and Bouyssou 1993). Methods based on score functions do not have a mechanism to detect and minimize this type of irregularity.

Leyva and Aguilera (2005) and Leyva and Araoz (2013) propose a mechanism showing an approach to minimizing inconsistency—in terms of pairwise rank reversal and incompleteness. In this paper, we extend this mechanism to the group multicriteria ranking problem under fuzzy outranking relations S ^σ _A . We give a characterization of fuzzy consistency based on the crisp consistency in a family of nested crisp outranking relations S ^λ _A (S ^λ _A  = {(a, b) ∊ A × A: σ(a, b) ≥ λ}, λ ∊ [λ ₀, 1]); these crisp relations correspond to λ-cuts of S ^σ _A , where the cutting level λ represents the minimum value for S ^σ _A such that aS ^λ _A b is true. This characterization facilitates the verification of pairwise rank reversal and completeness in the case of fuzzy outranking relations.

Using this characterization, we describe in the following a procedure that minimizes inconsistencies—in terms of pairwise rank reversal and incompleteness—between fuzzy outranking relations and the associated rankings.

1.1 Procedure

A potential solution of this type of ranking problem could be represented as an ordinal representation. In general, a potential solution $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}$ is a ranking of the set of decision alternatives by decreasing order of preference. These alternatives are joined together to form a ranking. The ranking is represented as the permutation of an m-ary alphabet where m is the number of alternatives in the decision problem. In such a representation, each alternative is coded into m-ary form. Alternatives are then linked together to produce one long m-ary permutation. An alternative coded with value $a_{{k_{i} }}$ in the ith entry of the permutation means that the alternative coded with value $a_{{k_{i} }}$ is ranked in the ith place of the ranking and $a_{{k_{i} }}$ is preferred to $a_{{k_{j} }}$ if i < j, where $a_{{k_{i} }} \, \in A = \{ a_{1} ,a_{2} , \ldots ,a_{m} \}$, i = 1, 2, …, m, and [k ₁, k ₂, …, k _m ] is a permutation of [1, 2, …, m].

Each potential solution $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}$ in the space of permutations is associated with a number λ (0 ≤ λ ≤ 1), which is connected with the credibility level of a crisp outranking relationship defined on the set of alternatives. We define the objective functions f and u of a permutation $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}$ with credibility level λ as follows: Let $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p} = a_{{k_{1} }} a_{{k_{2} }} \, \ldots \,a_{{k_{m} }}$ be the schematic representation of a potential solution (permutation) of the ranking problem, and suppose that given $a_{{k_{i} }}$ and $a_{{k_{j} }}$, two alternatives such that $\sigma (a_{{k_{i} }} ,a_{{k_{j} }} ) \ge \lambda$ and $\sigma (a_{{k_{j} }} ,a_{{k_{i} }} ) \le \lambda - \beta$ (β > 0, representing a threshold level), we accept that “$a_{{k_{i} }}$ outranks $a_{{k_{j} }}$” $(a_{{k_{i} }} \,S_{A}^{\lambda } a_{{k_{j} }} )$ and “$a_{{k_{j} }}$ does not outrank $a_{{k_{i} }}$” $(a_{{k_{j} }} nS_{A}^{\lambda } a_{{k_{i} }} )$. In this case, in the crisp outranking relationship generated by λ, S ^λ _A , a presumed preference favoring $a_{{k_{i} }}$, holds. Then:

$$\begin{aligned} f(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p} ) & = \left| {\left\{ {(a_{{k_{i} }} ,\,a_{{k_{j} }} ):a_{{k_{i} }} nS_{A}^{\lambda } a_{{k_{j} }} \;{\text{and}}\;a_{{k_{j} }} nS_{A}^{\lambda } a_{{k_{i} }} ;} \right.} \right. \\ & \quad \left. {\left. {i = 1,2, \ldots ,m - 1,\;j = 2,3, \ldots ,\,m,\quad i < j} \right\}} \right| \\ \end{aligned}$$

(2)

where [k ₁, k ₂, …, k _m ] is a permutation of [1, 2, …, m] and $f(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p} )$ is the number of incomparabilities between pairs of actions $(a_{{k_{i} }} ,a_{{k_{j} }} )$ in the permutation $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p} = a_{{k_{1} }} a_{{k_{2} }} \, \ldots \,a_{{k_{m} }}$ in the sense of the crisp relationship S ^λ _A . Note that the quality of potential solution $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}$ increases with decreasing f score.

The objective function u of a permutation $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}$ measures the amount of inconsistency (in relative terms); we chose to define it as follows:

$$\begin{aligned} u(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p} ) & = \left| {\left\{ {(a_{{k_{i} }} ,\,a_{{k_{j} }} ):a_{{k_{i} }} S_{A}^{\lambda } a_{{k_{j} }} \;{\text{and}}\;a_{{k_{j} }} nS_{A}^{\lambda } a_{{k_{i} }} ;} \right.} \right. \\ & \quad \left. {\left. {i = 1,2, \ldots ,\,m,\;j = 1,2, \ldots ,m,\quad i > j} \right\}} \right| \\ \end{aligned}$$

(3)

$u(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p} )$ is the number of preferences between alternatives in permutation $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}$ that are not “well-ordered” in the sense of S ^λ _A . $u(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p} )$ measures the amount of pairwise rank reversals between $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}$ and S ^λ _A .

A permutation $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}$ is consistent with respect S ^λ _A if $u(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p} ) = 0$ and inconsistent if $u(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p} ) > 0$. Defining the objective function u as taking the zero minimum value if and only if the solution is consistent seems a natural approach. Each permutation $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}$ can then be represented by a triad of values f, u, and λ. We are interested in the following:

• 1. Permutations whose objective function u value is equal to zero. This assures us that the ranking represented by the permutation is transitive; this is one of two characteristics that should be exhibited by all recommendations (solutions) of ranking problems (Vanderpooten 1990).

• 2. Permutations whose objective function f value is equal (or near) to zero. This objective improves the comparability of S on A.

• 3. Permutations whose credibility level λ is near to 1. This indicates that the ranking represented by the permutation with credibility level λ is more trustworthy whenever the objective functions u and f values are zero or near to zero. In practice, the requirement connected to function f does not permit λ values to approach 1 because in this case we could have many incomparable genes.

We want to solve the multiobjective combinatorial optimization problem:

$$\begin{aligned} & Min(u(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p} ),\quad Min(f(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p} )),\quad Max(\lambda ) \\ & Subject\,to \\ & \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p} \in Perm(A),\quad \lambda \in [0,1],\quad \lambda \ge \lambda_{0} \\ & (where\,Perm(A)\,is\,the\,set\,of\,permutations\,of\,A\,and\,\lambda_{0} \,is\,a \\ & {\text{minimum}}\,level\,of\,credibility) \\ \end{aligned}$$

(4)

Because of the structure of the multiobjective optimization problem (characterized by representation of a potential solution as a permutation of the elements of A, and the multiobjective and combinatorial nature), we use the evolutionary algorithm proposed in Leyva and Aguilera (2005) to exploit the fuzzy outranking relationship and to obtain a recommendation in the form of the most consistent ranking possible.

Appendix 2: Two procedures for the feedback mechanism based on multiobjective combinatorial optimization

In this appendix, we present two MOEAs based on a posterior articulation of preferences. These MOEAs are able to detect either the set of alternatives or the set of intercriteria parameters that a DM should consider to change their evaluation of a particular subset of criteria $\{ g_{{k_{1} }} ,g_{{k_{2} }} , \ldots ,g_{{k_{l} }} \}$, with the purpose of reducing pairwise disagreements between the dth order and the collective temporary order. The algorithms borrow fundamental elements from NSGA II (Deb et al. 2002). In the following subsections, after some basic definitions, we present in further detail fundamental aspects of the algorithms.

2.1 Basic definitions

Definition 1

Let A = {a ₁, a ₂, …, a _m } be a set of m alternatives and G = {g ₁, g ₂, …, g _n } be a set of n decision criteria defined on A. Without loss of generality, we can consider the first t criteria G _o  = {g ₁, g ₂, …, g _t } as objective criteria and the rest n − t criteria G _s  = {g _t+1, g _t+2, …, g _n } as subjective criteria. The performance matrix, denoted by M _d , of the dth DM, is the matrix of order m × n where the (i, j) entrance of M _d is g _j (a _i ).

Definition 2

The performance profile Q(a _i ) associated with action a _i  ∊ A is an n-tupla defined as follows:

$$Q\left( {a_{i} } \right) = \langle a_{i}^{1} , a_{i}^{2} , \ldots , a_{i}^{s} , \ldots , a_{i}^{n} \rangle \quad where,\,a_{i}^{s} = g_{s} \left( {a_{i} } \right).$$

Definition 3

Let K ^d be the set of pairwise disagreements between the dth order O ^d and the collective temporary order O ^G defined as follows:

$$K^{d} (O^{d} ,O^{G} ) = \left\{ {\begin{array}{*{20}l} {(a_{i} ,a_{j} ) \in A \times A|i < j,(O^{d} (a_{i} ) < O^{d} (a_{j} ) \wedge O^{G} (a_{i} ) > O^{G} (a_{j} )) \vee } \hfill \\ {(O^{d} (a_{i} ) > O^{d} (a_{j} ) \wedge O^{G} (a_{i} ) < O^{G} (a_{j} ))} \hfill \\ \end{array} } \right\}$$

The first complement of K ^d, K ^d,C _first , is the set of pairwise agreements between the first dth order O ^d and the collective temporary order O ^G and is defined as follows:

$$K_{first}^{d,C} (O^{d} ,O^{G} ) = \left\{ {\begin{array}{*{20}l} {(a_{i} ,a_{j} ) \in A \times A|i < j,(O^{d} (a_{i} ) < O^{d} (a_{j} ) \wedge O^{G} (a_{i} ) < O^{G} (a_{j} )) \vee } \hfill \\ {(O^{d} (a_{i} ) > O^{d} (a_{j} ) \wedge O^{G} (a_{i} ) > O^{G} (a_{j} ))} \hfill \\ \end{array} } \right\}$$

Note that $\left| {K^{d} } \right| + \left| {K_{first}^{d,C} } \right| = (m - 1)!$.

Definition 4

Let K ^d _M be the set of marginal pairwise disagreements between the dth order O ^d and the collective temporary order O ^G defined as follows:

$$\begin{aligned} K_{M}^{d} & = \left\{ {\left( {a_{i}^{s} , a_{j}^{s} } \right) \in Q\left( {a_{i} } \right)\left| {_{s} \times Q\left( {a_{j} } \right)} \right|_{s} |\left( {a_{i} , a_{j} } \right) \in K^{d} ,} \right. \\ & \quad i, j = 1, 2, \ldots ,m, i \ne j, s = 1, 2, \ldots , n\} , \\ \end{aligned}$$

where Q(a _i )| _s is the sth projection map of Q(a _i ).

Definition 5

An alternative a _i is feasible (firm) over a _j on a criterion g _k in the sense of a marginal strict preference relationship, denoted a _i P ^f _k a _j or a _j P ^f _k a _i , if the kth criterion is an objective criterion or the kth criterion is a subjective criterion and the dth DM is completely sure about this asseveration and will not change his/her preference during the consensus process. Let X _k be the set of pairs (a ^k _i , a ^k _j ) such that the alternative a _i is feasible over a _j on criterion g _k , i, j = 1, 2, …, m, k = 1, 2, …, n, i.e.:

$$X_{k} = \left\{ {\left( {a_{i}^{k} ,a_{j}^{k} } \right)|a_{i} P_{k}^{f} a_{j} \; \vee \;a_{j} P_{k}^{f} a_{i} ,\quad i,j = 1,2, \ldots ,m} \right\},\quad k = 1, 2, \ldots , n.$$

Let X be the set of pairs (a ^k _i , a ^k _j ) such that the alternative a _i is feasible over a _j , i, j = 1, 2,…, m, on at least one k = 1, 2, …, n i.e.:

$$X = \bigcup\limits_{k = 1}^{n} {X_{k} }$$

Let X _s be the set of pair (a ^k _i , a ^k _j ) such that the alternative a _i is feasible over a _j , i, j = 1, 2, …, m, on at least one subjective criterion g _k , k = t + 1, t + 2, …, n i.e.:

$$X_{s} = \bigcup\limits_{k = t + 1}^{n} {X_{k} } .$$

Definition 6

Let In_K ^d _M be the set of marginal pairwise disagreements between the dth order and the collective temporary order that are not feasible (or infeasible). It is defined as follows:

$$In\_K_{M}^{d} = K_{M}^{d} - X.$$

Definition 7

Let Fea_K ^d _M be the set of marginal pairwise disagreements between the dth order and the collective temporary order that are subjectively feasible. It is defined as follows:

$$Fea\_K_{M}^{d} = K_{M}^{d} \cap X_{s} .$$

The preferences will be changed using the following three rules:

• Rule 1 If O ^d(a _j ) − O ^G(a _j ) > 0, then increase evaluations associated to alternative a _j .

• Rule 2 If O ^d(a _j ) − O ^G(a _j ) = 0, do not change evaluations associated to alternative a _j .

• Rule 3 If O ^d(a _j ) − O ^G(a _j ) < 0, then decrease evaluations associated to alternative a _j .

2.2 A multiobjective evolutionary algorithm for identification of alternatives

We use a value-encoding scheme to represent a potential solution. In value encoding, each chromosome is represented as a string of some values. The values can be integer, real number, character or some object. Let $\tilde{p} = p_{1} p_{2} \, \ldots \,p_{mn}$ be the schematic representation of an individual’s chromosome, $\tilde{p} \in \prod\nolimits_{i = 1}^{mn} {C_{i} }$, where C _i is the set of values that p _i can take.

2.2.1 Objective functions f ₁, and f ₂

The fitness of an individual is calculated according to a given fitness procedure. The approach for defining an individual’s fitness involves the non-dominated solutions in a form similar to NSGA II (Deb et al. 2002). We define the objective function f ₁ of an individual $\tilde{p}$ as follows.

Let $\tilde{p} = p_{1} p_{2} \, \ldots \,p_{mn}$ be the schematic representation of an individual’s chromosome.

Let $\tilde{p}_{R} = r_{1} r_{2} \, \ldots \,r_{mn}$ be a reference individual representing the original performance matrix: r ₁ = g ₁(a ₁), r ₂ = g ₂(a ₁),…, r _n  = g _n (a ₁), r _n+1 = g ₁(a ₂), r _n+2 = g ₂(a ₂),…, r _2n  = g _n (a ₂), …, r _(m−1)n+1 = g ₁(a _m ), r _(m−1)n+2 = g ₂(a _m ), …, r _mn  = g _n (a _m ). Then:

$$f_{1} (\tilde{p}) = \left| {\left\{ {(p_{i} ,r_{i} )|\quad p_{i} \ne r_{i} \quad i = 1,2, \ldots ,mn} \right\}} \right|$$

$f_{1} (\tilde{p})$ is the number of modified marginal evaluations of alternatives. Note that the quality of solution increases with decreasing f ₁ score. With this objective function, we want to preserve, as much as possible, the original performance matrix.

The objective function f ₂ of an individual $\tilde{p}$ measures the amount of unfeasibility and subjective feasibility (in relative terms); we chose to define it as follows:

$$f_{2} (\tilde{p}) = \left| {In\_K_{M}^{d} } \right| + \left| {Fea\_K_{M}^{d} } \right|$$

$f_{2} (\tilde{p})$ is the number of infeasible marginal pairwise disagreements between the dth order and the collective temporary order plus the number of subjective feasible marginal pairwise disagreements between the dth order and the collective temporary order.

With this objective function we want to reduce pairwise disagreements between the dth order and the collective temporary order to increase the value of proximity measure wP ^d,G _A .

We include |Fea_K ^d _M | in the definition of f ₂ because we can modify the values of (a ^k _i , a ^k _j ) ∊ Fea_K ^d _M but always taking care to keep the original preferences given by the dth decision-maker, for the reason that an original preference (a ^k_* , a ^k_** ) ∊ Fea_K ^d _M , may be lost, where *, or ** can be i or j.

An individual $\tilde{p}$ is feasible if $f_{2} (\tilde{p}) = 0$ and infeasible if $f_{2} (\tilde{p}) > 0$. Defining the objective function f ₂ as taking the zero minimum value if and only if the solution is feasible seems a natural approach. We are interested in the following:

• 1. Individuals whose objective function f ₁ value is close to zero. This assures us that the ordering represented by the individual is almost equal to the original performance matrix; this is one characteristic always appreciated for all rational decision-makers.

• 2. Individuals whose objective function f ₂ value is close to zero. This objective improves feasibility and reduces the disagreements between the two orders.

Then, we use an evolutionary search to solve the multiobjective combinatorial problem:

$$\begin{aligned} & Min(f_{1} (\tilde{p})),\quad \;Min(f_{2} (\tilde{p})) \\ & Subject\;\;to \\ & \tilde{p} \in \prod\limits_{i = 1}^{mn} {C_{i} .} \\ \end{aligned}$$

2.3 A multiobjective evolutionary algorithm for identification of intercriteria parameters

We use a value-encoding scheme to represent a potential solution $\tilde{p}$. Let $\tilde{p} = p_{1} p_{2} \, \ldots \,p_{4n}$ be the schematic representation of an individual’s chromosome. $\tilde{p} \in \prod\nolimits_{i = 1}^{4n} {C_{i} }$, where C _i is the set of values that p _i can takes. This set of values is dependent of the problem. In Alvarez et al. (2015) is carried out a case study using this algorithm.

2.3.1 Objective functions f ₁, f ₂, and f ₃

The fitness of an individual is calculated according to a given fitness procedure. The approach for defining an individual’s fitness involves non-dominated solutions in a form similar to NSGA II (Deb et al. 2002). We define the objective function f ₁ of an individual $\tilde{p}$ as follows.

Let $\tilde{p} = p_{1} p_{2} \, \ldots \,p_{4n}$ be the schematic representation of an individual’s chromosome. Let $\tilde{p}_{R} = r_{1} r_{2} \, \ldots \,r_{4n}$ be a reference individual representing the original intercriteria parameters: r ₁ = w ₁, r ₂ = q ₁, r ₃ = p ₁, r ₄ = v ₁, r ₅ = w ₂, r ₆ = q ₂, …, r _4n−2 = q _n , r _4n−1 = p _n , …, r _4n  = v _n . Next, we have the following:

$$f_{1} (\tilde{p}) = \left| {\left\{ {(p_{i} ,r_{i} )|\quad p_{i} \ne r_{i} \quad i = 1,2, \ldots ,4n} \right\}} \right|$$

$f_{1} (\tilde{p})$ is the number of modified intercriteria parameters. Note that the quality of solution increases with decreasing f ₁ score. With this objective function, we want to preserve, as much as possible, the original intercriteria parameters.

The objective function f ₂ of an individual $\tilde{p}$ measures the amount of pairwise disagreements between the dth order O ^d and the collective temporary order O ^G; we chose to define it as follows:

$$f_{2} (\tilde{p}) = \left| {K^{d} } \right|$$

$f_{2} (\tilde{p})$ is the number of pairwise disagreements between the dth order and the collective temporary order.

With this objective function, we want to reduce pairwise disagreements between the dth order and the collective temporary order to increase the value of proximity measure wP ^d,G _A .

The objective function f ₃ of an individual $\tilde{p}$ measures the amount of pairwise agreements between the first dth order O ^d and the collective temporary order O ^G; we chose to define it as follows:

$$f_{3} (\tilde{p}) = \left| {K_{first}^{d,C} } \right|$$

$f_{3} (\tilde{p})$ is the number of pairwise agreements between the first dth order and the collective temporary order.

With this objective function, we want to maximize the original pairwise agreements between the dth order and the collective temporary order to preserve the rationality and values system of the DM.

We are interested in:

• 1. Individuals whose objective function f ₁ value tend to zero. This assures us that the ordering represented by the individual is almost equal to the original set of intercriteria parameters; this is one characteristic always appreciated for all rational decision-makers.

• 2. Individuals whose objective function f ₂ value tend to zero. This objective improves feasibility and reduces the disagreements between the two orders.

• 3. Individuals whose objective function f ₃ tend to (m − 1)! This assure us that the ordering represented by the individual increases the value of the proximity measure wP ^d,G _A .

Thus, we use an evolutionary search for solving the multiobjective combinatorial problem:

$$\begin{aligned} & Min(f_{1} (\tilde{p})),\quad Min(f_{2} (\tilde{p})),\quad Max(f_{3} (\tilde{p})) \\ & Subject\;to \\ & \tilde{p} \in \prod\limits_{i = 1}^{4n} {C_{i} }. \\ \end{aligned}$$