3D crack initiation and propagation applied to metal forming processes

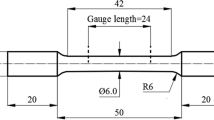
Abstract

Numerical simulation of ductile fracture in the field of metal forming represents one of the most challenging tasks. Throughout the chain of manufacturing processes, the accurate prediction of the crack surfaces is essential for the quality of the final products. The application of a crack initiation and propagation algorithm known as CIPFAR is presented in order to model the complex ductile fracture processes. In addition, a phase field approach is coupled with a ductile damage criterion to simulate the transition from damage to fracture. The self-contact between crack faces is also modeled through the penalization method in order to prevent the penetration of crack faces. The presented algorithm serves as an efficient computational tool for the industrial purposes in terms of the robustness and quality of the obtained results. Comparisons are carried out with the classical element deletion method in order to show the ability of the new algorithm to tackle the issues of mesh dependency and volume loss.

Appendix: Finite element model

In order to ensure the well-posedness and stability of the numerical solution, a bubble function is introduced to enrich the velocity field. The bubble function should have a value of 1 at the center of the element and vanishes at the boundaries. The approximate velocity, pressure and phase field variables can be expressed as

$$\begin{array}{@{}rcl@{}} v_{h} &=& v_{l} + v_{b} = \sum\limits_{k=1}^{N_{n}} {N_{l}^{k}} {v_{l}^{k}} + \sum\limits_{j=1}^{N_{e}} {N_{b}^{j}} {v}_{b}^{j} \end{array}$$

(29a)

$$\begin{array}{@{}rcl@{}} p_{h} &=& \sum\limits_{k=1}^{N_{n}} {N_{l}^{k}} P^{k} \end{array}$$

(29b)

$$\begin{array}{@{}rcl@{}} d_{h} &=& \sum\limits_{k=1}^{N_{n}} {N_{l}^{k}} d^{k} \end{array}$$

(29c)

where v_l and v_b are the linear and bubble velocities, respectively, p_h is the pressure and d_h is the phase field. ${N_{l}^{k}}$ and ${N_{b}^{j}}$ are the base and bubble interpolation functions associated with node k and element j, respectively. N_e and N_n are the number of elements and nodes respectively. The resulting problem in the general form can be written as

Find (v_h, p_h and d_h)

where $\vec {g}$ is the body load vector per unit mass, ρ is the density and ω_h is the volume of a finite element mesh in the current configuration so that

$$\omega_{h} = \bigcup_{e} \omega_{e} {(e \in N_{e})}.$$

The following properties are taken into account: ${\int \limits }_{\gamma _{t}} \vec {t} \cdot \delta v_{b} d{\omega _{h}} = 0$ since the bubble function vanishes at the boundaries, the inertial contribution of the bubble part is neglected so that ${\int \limits }_{\omega _{h}} \rho \frac {\partial v_{l}}{\partial t} \cdot \delta v_{b} d{\omega _{h}} = {\int \limits }_{\omega _{h}} \rho \frac {\partial v_{b}}{\partial t} \cdot \delta v_{l} d{\omega _{h}}= 0$ and ${\int \limits }_{\omega _{h}} \boldsymbol {s}(v_{b}) :\boldsymbol { \dot {\varepsilon }}(\delta v_{l}) d{\omega _{h}} = {\int \limits }_{\omega _{h}} \boldsymbol {s}(v_{l}) :\boldsymbol { \dot {\varepsilon }}(\delta v_{b}) d{\omega _{h}}= 0$ due to the orthogonality property of the bubble and nodal spaces. The time derivative of the velocity is approximated as follows

$$\begin{aligned}\frac{\partial v_{l,b}}{\partial t} =\frac{{v}^{ t+{\Delta} t}_{l,b} - {{v}^{ t}_{l,b}}}{\Delta t}\end{aligned}$$

(31)

where Δt is the time step. Substituting Eqs. A and 31 in Eqs. A–A, the final form of the residual equations can be written on the following form:

$$\begin{array}{@{}rcl@{}} \boldsymbol{R}^{ll} + \boldsymbol{R}^{lp} &=& \boldsymbol{0} \end{array}$$

(32a)

$$\begin{array}{@{}rcl@{}} \boldsymbol {R}^{bb}+ \boldsymbol{R}^{bp} &=& \boldsymbol{0} \end{array}$$

(32b)

$$\begin{array}{@{}rcl@{}} \boldsymbol{R}^{pl} + \boldsymbol{R}^{pb} + \boldsymbol{R}^{pp} &=& \boldsymbol{0} \end{array}$$

(32c)

$$\begin{array}{@{}rcl@{}} \boldsymbol{R}^{dd} + \boldsymbol{R}^{dl}&=& \boldsymbol{0} \end{array}$$

(32d)

where R^xy is the residual force vector of coupled set of unknowns x and y. The system of equations in (A) will be solved in a staggered manner. A Newton Raphson nonlinear solver is used to solve the system of the first three equations before each remeshing step. Then, the fourth equation will be solved independently. It is worth noting that the system of Eqs. 32a, 32b and 32c are condensated so that the final unknowns become the velocities and pressures at the nodes without the need to explicitly solve for the bubble velocities.