Buckling of rolled thin sheets under residual stresses by ANM and Arlequin method

Abstract

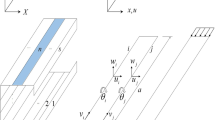
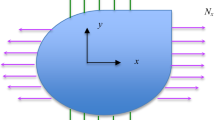
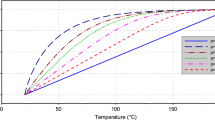
We present a numerical technique to model the buckling of a rolled thin sheet. It consists in coupling, within the Arlequin framework, a three dimensional model based on 8-nodes tri-linear hexahedron, used in the sheet part located upstream the roll bite, and a well-suited finite element shell model, in the roll bite downstream sheet part, in order to cope with buckling phenomena. The resulting nonlinear problem is solved by the Asymptotic Numerical Method (ANM) that is efficient to capture buckling instabilities. The originalities of the paper ly, first in an Arlequin procedure with moving meshes, second in an efficient application to a thin sheet rolling process. The suggested algorithm is applied to very thin sheet rolling scenarios involving “edges-waves” and “center-waves” defects. The obtained results show the effectiveness of our global approach.

Appendix A: Details of asymptotic numerical algorithm

Asymptotic Numerical Method (ANM) is a technique for solving nonlinear partial differential equations based on Taylor series with high truncation order. It has been proved to be an efficient method to deal with nonlinear problems in fluid and solid mechanics [19, 21–24, 26]. This technique consists in transforming a given nonlinear problem into a sequence of linear ones to be solved successively, leading to a numerical representation of the solution in the form of power series truncated at relatively high orders. Once the series are fully determined, an accurate approximation of the solution path is provided inside a determined validity range. Compared to iterative methods, ANM allows significant reduction of computation time since only one decomposition of the stiffness matrix is used to describe a large part of the solution branch without need of any iteration procedure. First, the procedure allows expanding the unknown variables of the problem in the form of power series with respect to a path parameter a and truncated at order N . For the considered problem 6, we set:

$$\begin{array}{@{}rcl@{}} \left( \begin{array}{c} u_{i}\\ \mu\\ \widetilde{\gamma}\\ \sigma\\ S\\ \lambda \\ \lambda_{res} \end{array}\right)&=& \left( \begin{array}{c} {u^{0}_{i}}\\ \mu^{0}\\\widetilde{\gamma}^{0}\\ \sigma^{0}\\ S^{0}\\ \lambda^{0} \\ \lambda^{0}_{res}\end{array}\right) + a\left( \begin{array}{c} {u_{i}^{1}}\\ \mu^{1}\\ \widetilde{\gamma}^{1}\\ \sigma^{1} \\ S^{1}\\ \lambda^{1} \\ \lambda^{1}_{res} \end{array}\right)+ a^{2}\left( \begin{array}{c} {u_{i}^{2}}\\ \mu^{2}\\ \widetilde{\gamma}^{2} \\ \sigma^{2} \\ S^{2}\\ \lambda^{2} \\ \lambda^{2}_{res} \end{array}\right)\\&&+ \cdot \ \cdot \ \cdot + a^{N}\left( \begin{array}{c} {u_{i}^{N}}\\ \mu^{N} \\ \widetilde{\gamma}^{N} \\ \sigma^{N} \\ S^{N} \\ \lambda^{N} \\ \lambda_{res}^{N} \end{array}\right) \end{array} $$

(12)

The series thus formed is composed of N sequences of the unknown variables and with the initial state of the problem given for order 0. For simplicity, we assume that there are no forces applied on the boundary of the coupling domain. In addition, by considering any vector $(\cdot )^{j}_{i}$, j denotes an asymptotic order and i represents the 3D domain (i = 1) or the shell domain (i = 2). Substituting (12) into (6), we obtain the following linear problem for order 1:

$$\begin{array}{@{}rcl@{}} \left\{\begin{array}{l} {\int}_{{\Omega}_{1}} \alpha_{1}{~}^{t} \sigma^{1} : \varepsilon(\delta u_{1}) \, \mathrm{d}{\Omega}+{\int}_{{\Omega}_{c}} \left\{\kappa \mu^{1} \delta u_{1} +\varepsilon(\mu^{1}):\mathbb{C}:\varepsilon(\delta u_{1}) \right\} \, \mathrm{d}{\Omega} =0 \\ \\ {\int}_{{\Omega}_{2}} \alpha_{2} \left\{ {~}^{t} S^{1} : \left[ \gamma^{l}(\delta u_{2})+2\gamma^{nl}\left( {u^{0}_{2}},\delta u_{2}\right) \right] + {~}^{t}S^{0}:2\gamma^{nl}\left( {u^{1}_{2}},\delta u_{2}\right) \right\} \, \mathrm{d}{\Omega} \\ \hspace{1cm}- {\int}_{{\Omega}_{c}} \left\{\kappa \mu^{1} \delta u_{2} +\varepsilon(\mu^{1}):\mathbb{C}:\varepsilon(\delta u_{2}) \right\} \, \mathrm{d}{\Omega}=\lambda^{1} {\int}_{{\Omega}_{2}} f \delta u_{2} \, \mathrm{d}{\Gamma} \\ \\ {\int}_{{\Omega}_{c}(x_{0})} \left\{\kappa \delta \mu {u^{1}_{1}} +\varepsilon(\delta \mu):\mathbb{C}:\varepsilon\left( {u^{1}_{1}}\right) \right\} \, \mathrm{d}{\Omega} - {\int}_{{\Omega}_{c}(x_{0})} \left\{\kappa \delta \mu {u^{1}_{2}} +\varepsilon(\delta \mu):\mathbb{C}:\varepsilon\left( {u^{1}_{2}}\right) \right\} \, \mathrm{d}{\Omega}=0\\ \\ {\int}_{{\Omega}_{2}} {~}^{t}S^{1}:\delta \widetilde{\gamma} \, \mathrm{d}{\Omega}=0\\ \\ \sigma^{1}= \mathbb{C}:\varepsilon^{1} + \lambda^{1}_{res} \sigma^{res} \\ S^{1}= \mathbb{C}: \left[ \gamma^{l}\left( {u_{2}^{1}}\right)+2\gamma^{nl}\left( {u^{1}_{2}},{u_{2}^{0}}\right) + \widetilde{\gamma}^{1} \right]+ \lambda^{1}_{res} S^{res} \end{array}\right. \end{array} $$

(13)

Similarly, we can derive the following linear problem for order k (1 < k ≤ N)

$$\begin{array}{@{}rcl@{}}</p><p class="noindent">\left\{\begin{array}{l} {\int}_{{\Omega}_{1}} \alpha_{1}{~}^{t} \sigma^{k} : \varepsilon(\delta u_{1}) \, \mathrm{d}{\Omega}+{\int}_{{\Omega}_{c}} \left\{\kappa \mu^{k} \delta u_{1} +\varepsilon(\mu^{k}):\mathbb{C}:\varepsilon(\delta u_{1}) \right\} \, \mathrm{d}{\Omega} =0 \\ \\ {\int}_{{\Omega}_{2}} \alpha_{2} \left\{ {~}^{t} S^{k} : \left[ \gamma^{l}(\delta u_{2})+2\gamma^{nl}({u^{0}_{2}},\delta u_{2}) \right] + {~}^{t}S^{0}:2\gamma^{nl}\left( {u^{k}_{2}},\delta u_{2}\right) \right\} \, \mathrm{d}{\Omega} \\ \hspace{1cm}- {\int}_{{\Omega}_{c}} \left\{\kappa \mu^{k} \delta u_{2} +\varepsilon(\mu^{k}):\mathbb{C}:\varepsilon(\delta u_{2}) \right\} \, \mathrm{d}{\Omega}=\lambda^{k} {\int}_{{\Omega}_{2}} f \delta u_{2} \, \mathrm{d}{\Gamma} \\ \hspace{1cm} - {\int}_{{\Omega}_{2}}{\sum}_{j=1}^{k-1} \left ({~}^{t}S^{j}:2\gamma^{nl}\left( u^{k-j}_{2},\delta u_{2}\right) \right ) \\ \\ {\int}_{{\Omega}_{c}(x_{0})} \left\{\kappa \delta \mu {u^{k}_{1}} +\varepsilon(\delta \mu):\mathbb{C}:\varepsilon\left( {u^{k}_{1}}\right) \right\} \, \mathrm{d}{\Omega} - {\int}_{{\Omega}_{c}(x_{0})} \left\{\kappa \delta \mu {u^{k}_{2}} +\varepsilon(\delta \mu):\mathbb{C}:\varepsilon\left( {u^{k}_{2}}\right) \right\} \, \mathrm{d}{\Omega}=0\\ \\ {\int}_{{\Omega}_{2}} {~}^{t}S^{k}:\delta \widetilde{\gamma} \, \mathrm{d}{\Omega}=0\\ \\ \sigma^{k} = \mathbb{C}:\varepsilon^{k} + \lambda^{k}_{res} \sigma^{res}\\ S^{k} = \mathbb{C}: \left[ \gamma^{l}\left( {u_{2}^{k}}\right)+2\gamma^{nl}\left( {u^{k}_{2}},{u_{2}^{0}}\right) + {\sum}_{j=1}^{k-1} \gamma^{nl}\left( u^{k-j}_{2},{u_{2}^{j}}\right) + \widetilde{\gamma}^{k} \right]+ \lambda^{k}_{res} S^{res} \end{array}\right. \end{array} $$

(14)

To solve the system of Eqs. 13 and 14, an additional equation is needed. In this work, we introduce a condition similar to the arc-length type continuation condition:

$$ a=<\left\{ u_{1}\\ u_{2}\right\}-\left\{ {u^{0}_{1}}\\ {u^{0}_{2}}\right\},\left\{ {u^{1}_{1}}\\ {u^{1}_{2}}\right\}> $$

(15)

where < ., > denotes the scalar product for two vectors.

For the continuation procedure, reader can refer to references [21, 25, 26].