Hydro-mechanical loading and compressibility of fibrous media for resin infusion processes

Abstract

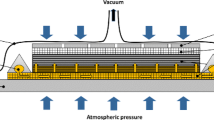
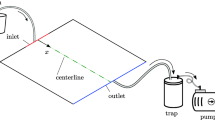
The modelling of composite manufacturing processes where hydro-mechanical coupling takes place depends on the validity of compressibility and permeability models. In this work, the computer code initially used to simulate the effect of coupled hydro-mechanical load on composite preform (Ouahbi et al. Composites Part A, 38:1646–1654, 2007) is integrated into an inverse method to predict the compaction behaviour of the reinforcements. An experimental device developed at Le Havre is used to apply hydro-mechanical loads to the preforms. Two ramps of stress are imposed to the preform and the thickness evolution is measured as a function of time. The speed of thickness reduction is not constant and varies in the range of 0.1 to 12 mm/min. The effect of compression speed upon the saturated fabrics is investigated. For a fixed fibre volume fraction, an increase in stress is observed in increasing compression speed. The experimental results are compared to the compressibility curves determined by an inverse method. The calculated curves correspond to the compressibility curves experimentally obtained with low compression speed (∼0.25 mm/min). As a consequence, this suggests that a low compression speed should be applied when investigating the compressibility behaviour of composite preform with a view of modelling resin infusion processes.

Appendix A

The mass conservation equations of resin and fibre, in transverse analysis, can be written respectively as:

$$ \begin{array}{*{20}{c}} {{\text{Fluid}}\,{\text{phase}}} \hfill & {\frac{{\partial \phi }}{{\partial t}} + \frac{\partial }{{\partial z}}\left( {\phi \frac{{\partial V}}{{\partial t}}} \right) = 0} \hfill \\ \end{array} $$

(A.1)

$$ \begin{array}{*{20}{c}} {{\text{Solid}}\,{\text{phase}}} \hfill & {\frac{{\partial \left( {1 - \phi } \right)}}{{\partial t}} + \frac{\partial }{{\partial z}}\left( {\left( {1 - \phi } \right)\frac{{\partial U}}{{\partial t}}} \right) = 0} \hfill \\ \end{array} $$

(A.2)

Where ϕ is the porosity of the medium, with ϕ = 1−V _f , V the displacement of the fluid and U the displacement of the reinforcement.

The relative displacement of fluid W is defined by: W(M,t) = V(M,t)−U(M,t)

Equation (A.1) can be rewritten using the relative displacement of fluid:

$$ \frac{{\partial \phi }}{{\partial t}} + \frac{\partial }{{\partial z}}\left( {\phi \frac{{\partial W}}{{\partial t}} + \phi \frac{{\partial U}}{{\partial t}}} \right) = 0 $$

(A.3)

The velocities are introduced: ${u_s} = \frac{{\partial U}}{{\partial t}}$, ${q_f} = \frac{{\partial V}}{{\partial t}}$ and $q = \phi \frac{{\partial W}}{{\partial t}}$

Equation (A.3) can be expressed as a function of the velocities:

$$ \frac{{\partial \phi }}{{\partial t}} + \frac{{\partial q}}{{\partial z}} + \phi \frac{{\partial {u_s}}}{{\partial z}} + {u_s}\frac{{\partial \phi }}{{\partial z}} = 0 $$

(A.4)

Solid phase equation (A.2) can be expressed as:

$$ \frac{{\partial \left( {1 - \phi } \right)}}{{\partial t}} + \left( {1 - \phi } \right)\frac{{\partial {u_s}}}{{\partial z}} - {u_s}\frac{{\partial \phi }}{{\partial z}} = 0 $$

(A.5)

The mass conservation equation is described by the following combination of Eqs. A.4 and A.5: $\left( {1 - \phi } \right) \cdot \left( {A.4} \right) - \left( \phi \right) \cdot \left( {A.5} \right)$

$$ \frac{{\partial q}}{{\partial z}} = - \frac{1}{{1 - \phi }}\left( {\frac{{\partial \phi }}{{\partial t}} + {u_s}\frac{{\partial \phi }}{{\partial z}}} \right) $$

(A.6)

Equation (A.6) can be expressed as a function of fibre volume fraction as $\frac{{\partial {V_f}}}{{\partial t}} = - \frac{{\partial \varphi }}{{\partial t}}$:

$$ \frac{{\partial q}}{{\partial z}} = \frac{1}{{{V_f}}}\left( {\frac{{\partial {V_f}}}{{\partial t}} + {u_s}\frac{{\partial {V_f}}}{{\partial z}}} \right) $$

(A.7)

It can be shown that $\frac{1}{{{V_f}}}\frac{{\partial {V_f}}}{{\partial z}}{u_s}$ can be neglected in comparison to the other term of the governing equation$\frac{1}{{{V_f}}}\frac{{\partial {V_f}}}{{\partial t}}$. To demonstrate this, a non dimensional number $\beta = \left( {\frac{{\partial {V_f}}}{{\partial z}}{u_s}} \right)/\left( {\frac{{\partial {V_f}}}{{\partial t}}} \right)$ is plotted as a function of the compression speed and the evolution of the thickness (from 1 no compression to 0 that corresponds to a full compression i.e.: no space for the reinforcement).

In any of the plotted conditions, the value of β is very low (in the 10⁻⁴ range), and therefore it is normal to neglect the term $\frac{1}{{{V_f}}}\frac{{\partial {V_f}}}{{\partial z}}{u_s}$ in comparison to the term $\frac{1}{{{V_f}}}\frac{{\partial {V_f}}}{{\partial t}}$in the sum of the governing equation.

Equation (A.7) can therefore be simplified:

$$ \frac{{\partial q}}{{\partial z}} = \frac{1}{{{V_f}}}\left( {\frac{{\partial {V_f}}}{{\partial t}}} \right) $$

(A.8)