The Harmonicity of Slice Regular Functions

Abstract

In this article, we investigate harmonicity, Laplacians, mean value theorems, and related topics in the context of quaternionic analysis. We observe that a Mean Value Formula for slice regular functions holds true and it is a consequence of the well-known Representation Formula for slice regular functions over ${\mathbb {H}}$. Motivated by this observation, we have constructed three order-two differential operators in the kernel of which slice regular functions are, answering positively to the question: is a slice regular function over ${\mathbb {H}}$ (analogous to an holomorphic function over ${\mathbb {C}}$) ”harmonic” in some sense, i.e., is it in the kernel of some order-two differential operator over ${\mathbb {H}}$? Finally, some applications are deduced such as a Poisson Formula for slice regular functions over ${\mathbb {H}}$ and a Jensen’s Formula for semi-regular ones.

1 Introduction

In [20] and [21], Gentili and Struppa gave the following definition of slice regular function over the quaternions:

Definition 1.1

Let $\Omega$ be a domain in ${{\mathbb {H}}}$. A real differentiable function $f :\Omega \rightarrow {{\mathbb {H}}}$ is said to be slice regular if, $\forall \,\, I \in {\mathbb {S}}=\{ q \in {{\mathbb {H}}}, \, \mathfrak {R}(q)=0 \, : \, |q| =1 \}$, its restriction $f_{I}$ to the complex line ${{\mathbb {C}}}_I= {\mathbb {R}} + {\mathbb {R}} I$ passing through the origin and containing 1 and I is holomorphic on $\Omega \cap {{\mathbb {C}}}_I$, which is equivalent to require that, $\forall \, I \, \in {\mathbb {S}},$

$$\begin{aligned} {\overline{\partial }}_I f (x+yI) := \frac{1}{2} ( \frac{\partial }{\partial x} + I \frac{\partial }{\partial y})f_I (x+yI)=0 \end{aligned}$$

(1)

on $\Omega \cap {{\mathbb {C}}}_I.$

Later the notion of “slice regularity” was generalized to algebras other than ${{\mathbb {H}}}$ [16, 23].

For simplicity, sometimes slice regular functions are simply called “regular functions.”

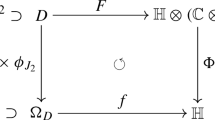
Let $D\subset {\mathbb {C}}$ be any symmetric set with respect to the real axis. A function $F=F_{1}+ F_{2}\imath :D\rightarrow {{\mathbb {H}}}\otimes {{\mathbb {C}}}$ such that $F({\overline{z}})=\overline{F(z)}$ is said to be a stem function.

Let $\Omega _D=\{\alpha +\beta I:\alpha ,\beta \in {{\mathbb {R}}}, I\in {\mathbb {S}}, \alpha +\beta i\in D\}$.

A function $f:\Omega _{D}\rightarrow {{\mathbb {H}}}$ is said to be a (left) slice function if it is induced by a stem function $F=F_{1}+F_2\imath$ defined on D in the following way: for any $\alpha +I\beta \in \Omega _{D}$,

$$\begin{aligned} f(\alpha +I\beta )=F_{1}(\alpha +i\beta )+I F_{2}(\alpha +i\beta ). \end{aligned}$$

If a stem function F induces the slice function f, we will write $f={\mathcal {I}}(F)$.

Proposition 1.2

Let D be a symmetric domain in ${{\mathbb {C}}}$ which intersects ${{\mathbb {R}}}$ and let $\Omega _D\subset {{\mathbb {H}}}$ be defined as above.

Then a slice function $f:\Omega _D\rightarrow {{\mathbb {H}}}$ is slice regular if and only if its stem function $F:D\rightarrow {{\mathbb {H}}}\otimes {{\mathbb {C}}}$ is holomorphic.

(See Proposition 8 of [23].)

These notions have been studied a lot in the last years: see, for example, the many results for slice regular functions from the unit ball of ${{\mathbb {H}}}$ to itself: [7,8,9,10,11] and for entire slice regular functions [13].

Classically, mean value theorems are closely related to harmonicity. We investigate mean value properties for quaternionic functions. We prove (Proposition 4.1) that a slice regular function f fulfills

$$\begin{aligned} f(a+bI) =\frac{1}{2\pi } \int _{\mathbb {S}}\int _0^{2\pi } (1-IJ)f(a+bJ+re^{J\theta }) \mathrm{{d}}\theta \mathrm{{d}}\mu (J), \ \forall a,b\in {{\mathbb {R}}}, I\in {\mathbb {S}}, \end{aligned}$$

where $\mu$ is a probability measure on ${\mathbb {S}}$ which is invariant under the involution $J\mapsto -J$.

Conversely, we show that every continuous function $f:{{\mathbb {H}}}\rightarrow {{\mathbb {H}}}$ with this mean value property must be the sum of a regular and an anti-regular function (Theorem 4.4).

We also show that for any point $p\in {{\mathbb {H}}}$ and every 3-sphere S containing p in the interior, there exists a ${{\mathbb {H}}}$-valued measure on S such that $f(p)=\int _S f(q)\mathrm{{d}}\mu (q)$ for every slice regular function f (Theorem 7.1).

Over the field of complex numbers, the mean value property is equivalent to harmonicity. Therefore it is natural ask ourselves if slice regular functions were in the kernel of some order-two differential operator over ${{\mathbb {H}}}$: in Sect. 8 we answer positively to this question constructing three order-two differential operators in the kernel of which slice regular functions are.

The first one is $\Delta _*$, introduced in Definition 6.15. For slice functions it is defined everywhere, for other functions only outside ${{\mathbb {R}}}$. On each slice ${{\mathbb {C}}}_I$ the operator $\Delta _*$ acts as the complex Laplacian if we identify ${{\mathbb {C}}}_I\simeq {{\mathbb {C}}}$ and ${{\mathbb {H}}}={{\mathbb {C}}}_I\oplus J{{\mathbb {C}}}_I \simeq {{\mathbb {C}}}^2$ (with J being an imaginary unit orthogonal to I). If f is a slice function, then $\Delta _*(f)$ is again a slice function and $\Delta _*(f)={\mathcal {I}}(\Delta F)$ for $f={\mathcal {I}}(F)$.

The second order-two differential operator is $\Delta '$:

$$\begin{aligned} (\Delta 'f)(q)=\left( \Delta _* \int _{{\mathbb {S}}}R_wf\mathrm{{d}}\mu (w)\right) (q) \end{aligned}$$

Here $R_w$ is an averaging operator which we define based on rotations, cf. Sect. 6. We observe that $(\Delta ' f)(q)=\frac{1}{2}\Delta _* (Tr(f))(q)= \frac{1}{2}\Delta _* (f+f^c)(q)$. For the definition of $f^c$ see Definition 2.10.

The third order-two differential operator is $\Delta ''$:

$$\begin{aligned} (\Delta '' f)(q)=(\Delta _* N(f))(q)=(\Delta _* (f \cdot f^c)) (q) \end{aligned}$$

On one side $\Delta _*$ and $\Delta '$ are ${\mathbb {R}}-$linear operator, on the other hand $\Delta ''$ is not a linear operator but for $\Delta ''$ a sort of Leibnitz rule for $(f * g)$ holds true (Proposition 6.25). For the definition of slice product, denoted with $*$, see Definition 2.7.

Our main results on $\Delta _*$ and $\Delta '$ are the following :

Theorem 1.3

(Theorem 6.22) Let $f:\Omega _D\rightarrow {{\mathbb {H}}}$ be a $C^2$ slice function. Assume that D is simply connected.

$\Delta _*f$ is vanishing identically if and only if f can be written as a sum of a regular function g and an anti-regular function h.

For the definition of anti-regular function see Remark 2.5.

Proposition 1.4

(Proposition 6.31) Let $h:{{\mathbb {H}}}\rightarrow {\mathbb {R}}$ be a slice function with $\Delta 'h=0$. Then there exists a slice-preserving regular function f such that $h=\mathfrak {R}\, (f)$.

Proposition 1.5

(Proposition 6.34) Let $u :{{\mathbb {H}}}\rightarrow {\mathbb {R}}$ be a $C^2$-function such that $\Delta ' u=0$ outside ${{\mathbb {R}}}$.

Then u admits no isolated zero in any real point $a\in {{\mathbb {R}}}$.

Finally, we provide a Jensen’s formula.

Proposition 1.6

(Jensen’s Formula; Proposition 8.7) Let $\Omega =\Omega _D$ be a circular domain of ${{\mathbb {H}}}$ and let $f:\Omega \rightarrow {{\mathbb {H}}}\cup \{ \infty \}$ be a semi-regular function. Let $\rho >0$ be such that the ball, centered in 0 and of radius $\rho ,$ $\overline{{\mathbb {B}}_{\rho }}\subset \Omega$, $f(0)\ne 0,\infty$ and such that $f(y)\ne 0, \infty$, for any $y\in \partial {\mathbb {B}}_{\rho }$. Let $\mu$ be a probability measure on ${\mathbb {S}}$.

Then:

$$\begin{aligned} \log |f(0)|\le & {} \displaystyle \frac{1}{2\pi \mu ({\mathbb {S}})}\displaystyle \int _0^{2\pi } \int _{{\mathbb {S}}}\log |f(\rho \cos \theta +\rho \sin \theta I)|\mathrm{{d}}\mu (I)\mathrm{{d}}\theta \, + \nonumber \\&\quad \displaystyle -\sum _{|p_k|<\rho } m_k\log \frac{\rho }{|p_k|} \end{aligned}$$

(2)

for $div(f)=\sum m_k\{p_k\}$.

We hope that this paper can provide new ideas for studying slice regular functions and their “harmonic properties” on slice regular quaternionic manifolds recently introduced by Bisi-Gentili in [12] and Angella-Bisi in [5].

2 Prerequisites About Quaternionic Functions

In this section, we will overview the main notions and results needed for our aims. First of all, let us denote by ${\mathbb {H}}$ the real algebra of quaternions. An element $x\in {{\mathbb {H}}}$ is usually written as $x=x_{0}+ix_{1}+jx_{2}+kx_{3}$, where $i^{2}=j^{2}=k^{2}=-1$ and $ijk=-1$. Given a quaternion x we introduce a conjugation in ${{\mathbb {H}}}$ (the usual one), as $x^{c}=x_{0}-ix_{1}-jx_{2}-kx_{3}$; with this conjugation we define the real part of x as $\mathfrak {R}(x):=(x+x^{c})/2$ and the imaginary part as $\mathfrak {I}(x):=(x-x^{c})/2$. With the notion of conjugation just defined we can write the euclidean square norm of a quaternion x as $|x|^{2}=xx^{c}$. The subalgebra of real numbers will be identified, of course, with the set ${\mathbb {R}}:=\{x\in {{\mathbb {H}}}\,\mid \,\mathfrak {I}(x)=0\}.$

Now, if $x\in {{\mathbb {H}}}\setminus {\mathbb {R}}$ is such that $\mathfrak {R}(x)=0$, then the imaginary part of x is such that $(\mathfrak {I}(x)/|\mathfrak {I}(x)|)^{2}=-1$. More precisely, any imaginary quaternion $I=ix_{1}+jx_{2}+kx_{3}$, such that $x_{1}^{2}+x_{2}^{2}+x_{3}^{2}=1$ is an imaginary unit. The set of imaginary units is then a real $2-$sphere and it will be conveniently denoted as follows:

$$\begin{aligned} {\mathbb {S}}:=\{x\in {{\mathbb {H}}}\,\mid \, x^{2}=-1\}=\{x\in {{\mathbb {H}}}\,\mid \, \mathfrak {R}(x)=0, \, |x|=1\}. \end{aligned}$$

With the previous notation, any $x\in {{\mathbb {H}}}$ can be written as $x=\alpha +I\beta$, where $\alpha ,\beta \in {\mathbb {R}}$ and $I\in {\mathbb {S}}$. Given any $I\in {\mathbb {S}}$ we will denote the real subspace of ${{\mathbb {H}}}$ generated by 1 and I as

$$\begin{aligned} {\mathbb {C}}_{I}:=\{x\in {{\mathbb {H}}}\,\mid \,x=\alpha +I\beta , \alpha ,\beta \in {\mathbb {R}}\}. \end{aligned}$$

Sets of the previous kind will be called slices.

We denote the $2-$sphere with center $\alpha \in {\mathbb {R}}$ and radius $|\beta |$ (passing through $\alpha +I\beta \in {{\mathbb {H}}}$), as

$$\begin{aligned} {\mathbb {S}}_{\alpha +I\beta }:=\{x\in {{\mathbb {H}}}\,\mid \,x=\alpha +J\beta , J\in {\mathbb {S}}\}. \end{aligned}$$

Obviously, if $\beta =0$, then ${\mathbb {S}}_{\alpha }=\{\alpha \}$.

2.1 Slice Functions and Regularity

In this part we will recall the main definitions and features of slice functions. The theory of slice functions was introduced in [23] as a tool to generalize the theory of quaternionic regular functions defined on particular domains introduced in [20, 21], to more general domains and to alternative $*$-algebras.

The complexification of ${{\mathbb {H}}}$ is defined to be the real tensor product between ${{\mathbb {H}}}$ itself and ${\mathbb {C}}$:

$$\begin{aligned} {{\mathbb {H}}}_{{\mathbb {C}}}:={{\mathbb {H}}}\otimes _{{\mathbb {R}}}{\mathbb {C}}:=\{p+q\imath \,\mid \, p,q\in {{\mathbb {H}}}\}. \end{aligned}$$

(Here $\imath =1 \otimes i$.) Note that ${{\mathbb {H}}}\otimes {{\mathbb {C}}}$ has a natural structure of an associative algebra induced by the algebra structures of ${{\mathbb {H}}}$ and ${{\mathbb {C}}}$. Explicitly, the product on ${{\mathbb {H}}}\otimes {{\mathbb {C}}}$ is given as follows: if $p_{1}+ q_{1}\imath , p_{2}+ q_{2}\imath$ belong to ${{\mathbb {H}}}\otimes {{\mathbb {C}}}$, then,

$$\begin{aligned} (p_{1}+ q_{1}\imath )(p_{2}+ q_{2}\imath )=p_{1}p_{2}-q_{1}q_{2}+(p_{1}q_{2}+q_{1}p_{2})\imath . \end{aligned}$$

The usual complex conjugation $\overline{p+q\imath }=p-q\imath$ commutes with the following involution (the quaternionic conjugation) $(p+q\imath )^{c}=p^{c}+ q^{c}\imath$.

We introduce now the class of subsets of ${{\mathbb {H}}}$ where our functions will be defined.

Definition 2.1

Given any set $D\subseteq {\mathbb {C}}$, we define its circularization as the subset in ${{\mathbb {H}}}$ defined as follows:

$$\begin{aligned} \Omega _{D}:=\{\alpha +I\beta \,\mid \,\alpha ,\beta \in {{\mathbb {R}}}, \alpha +i\beta \in D, I\in {\mathbb {S}}\}. \end{aligned}$$

Such subsets of ${{\mathbb {H}}}$ are called circular sets. If $D\subset {\mathbb {C}}$ is an open connected subset such that $D\cap {\mathbb {R}}\ne \emptyset$, then $\Omega _{D}$ (which is again open and connected and intersects the real line ${{\mathbb {R}}}$) is called a slice domain (see [22]).

Note that for any subset $D\subset {{\mathbb {C}}}$ the circularization $\Omega _D$ coincides with the circularization $\Omega _{D^s}$ of the symmetrized domain $D^s=\{z:z\in D\text { or } {\bar{z}}\in D\}$.

From now on, $\Omega _{D}\subset {{\mathbb {H}}}$ will always denote a circular domain arising as circularization of a symmetric domain $D\subset {{\mathbb {C}}}$.

Definition 2.2

Let $D\subset {\mathbb {C}}$ be any symmetric set with respect to the real axis. A function $F=F_{1}+F_2\imath :D\rightarrow {{\mathbb {H}}}\otimes {{\mathbb {C}}}$ such that $F({\overline{z}})=\overline{F(z)}$ is said to be a stem function.

A function $f:\Omega _{D}\rightarrow {{\mathbb {H}}}$ is said to be a (left) slice function if it is induced by a stem function $F=F_{1}+F_2\imath$ defined on D in the following way:

$$\begin{aligned} f(\alpha +I\beta )=F_{1}(\alpha +i\beta )+I F_{2}(\alpha +i\beta ) \end{aligned}$$

(3)

for all $\alpha +i\beta \in D$ and all $I\in {\mathbb {S}}$. If a stem function F induces the slice function f, we will write $f={\mathcal {I}}(F)$. The set of slice functions defined on a certain circular domain $\Omega _{D}$ will be denoted by ${\mathcal {S}}(\Omega _{D})$.

Lemma 2.3

Let $f:\Omega _D\rightarrow {{\mathbb {H}}}$ be a function defined on a circular domain $\Omega _D$. If there exists a function $F=F_1+F_2\imath : D\rightarrow {{\mathbb {H}}}\otimes {{\mathbb {C}}}$ such that Eq. (3) holds, then F is a stem function, i.e., $F_1(z)=F_1({\bar{z}})$ and $F_2( z)=-F_2({\bar{z}})$.

Proof

We observe that for all $z=\alpha +i \beta \in D$ and all $I\in {\mathbb {S}}$ we have

$$\begin{aligned} f(\alpha +I\beta )=F_{1}(\alpha +i\beta )+I F_{2}(\alpha +i\beta ) \end{aligned}$$

and

$$\begin{aligned} f(\alpha +(-I)(-\beta ))=F_{1}(\alpha -i\beta )-I F_{2}(\alpha -i\beta ), \end{aligned}$$

implying the statement. $\square$

Examples of (left) slice functions are polynomials and functions given by power series in the variable $x\in {{\mathbb {H}}}$ with all coefficients on the right, i.e., a power series

$$\begin{aligned} \sum _{k=0}^{+ \infty } x^{k}a_{k},\quad \{a_{k}\}\subset {{\mathbb {H}}}, \end{aligned}$$

if convergent, defines a slice function.

A function $f:\Omega _D\rightarrow {{\mathbb {H}}}$ is a slice function if and only if it obeys the following “representation formula”:

$$\begin{aligned} f(x+yJ)=\frac{1-JI}{2}f(x+yI)+ \frac{1+JI}{2}f(x-yI)\,\, \forall x,y\in {{\mathbb {R}}}, \,\, \forall I,J\in {\mathbb {S}}\end{aligned}$$

(see [22, 23]).

2.1.1 Regularity

Let now $D\subset {\mathbb {C}}$ be an open set and $z=\alpha +i\beta \in D$. Given a stem function $F=F_1+F_2\imath :D\rightarrow {\mathbb {H}}_{\mathbb {C}}$ of class $C^1$, then

$$\begin{aligned} \frac{\partial F}{\partial z},\frac{\partial F}{\partial \bar{z}}:D\rightarrow {\mathbb {H}}_{\mathbb {C}}\simeq {{\mathbb {C}}}^4, \end{aligned}$$

are defined as usual, i.e.,

$$\begin{aligned} \frac{\partial F}{\partial z}=\frac{1}{2}\left( \frac{\partial F}{\partial \alpha }-\imath \frac{\partial F}{\partial \beta }\right) \quad \text{ and } \quad \frac{\partial F}{\partial \bar{z}}=\frac{1}{2}\left( \frac{\partial F}{\partial \alpha }+\imath \frac{\partial F}{\partial \beta }\right) . \end{aligned}$$

They are again stem functions.

Let f be a slice function induced by a stem function F (i.e., $f={\mathcal {I}} (F)$) and let $q\in {{\mathbb {H}}}$, $q\in {{\mathbb {C}}}_I$, $I\in {\mathbb {S}}$.

Then

$$\begin{aligned} (\partial _If)(q)={\mathcal {I}}\left( \frac{\partial F}{\partial z}\right) (q), \quad ({{\bar{\partial }}}_If)(q)= {\mathcal {I}}\left( \frac{\partial F}{\partial {\overline{z}}}\right) (q). \end{aligned}$$

(4)

These derivatives are also called “Cullen derivatives.”

We are now in the position to define slice regular functions (see Definition 8 in [23]).

Definition 2.4

Let $\Omega _{D}$ be a circular open set. A slice function $f={\mathcal {I}}(F)\in {\mathcal {S}}(\Omega _{D})$ is (left) regular if its stem function F is holomorphic. The set of regular functions will be denoted by

$$\begin{aligned} {{\mathcal {S}}}{{\mathcal {R}}}(\Omega _{D}):=\{f\in {\mathcal {S}}(\Omega _{D})\,|\,f={\mathcal {I}}(F), \,\,\, F:D\rightarrow {{\mathbb {H}}}\otimes {{\mathbb {C}}} \text{ holomorphic }\}. \end{aligned}$$

The set of regular functions is a real vector space and a right ${{\mathbb {H}}}$-module. In the case in which $\Omega _{D}$ is a slice domain, the definition of regularity is equivalent to the one given in [22].

Remark 2.5

A function $f={\mathcal {I}}(F)\in {\mathcal {S}}^{1}(\Omega _{D})$ is called (left) anti-regular if its stem function F is anti-holomorphic.

We recall a key lemma of this theory that will be useful later on, [22].

Lemma 2.6

(Splitting) Let f be a regular function defined on an open set $\Omega$ of ${\mathbb {H}}.$ Then, for any $I \in {\mathbb {S}}$ and for any $J \in {\mathbb {S}}$ with $J \perp I,$ there exist two holomorphic functions $g_I,h_I :\Omega \cap {\mathbb {C}}_I \rightarrow {\mathbb {C}}_I$ such that, $\forall z = x + y I$, it is

$$\begin{aligned} f_I (z)=g_I(z)+h_I(z)J, \end{aligned}$$

where $f_I$ is the restriction of f to ${\mathbb {C}}_I.$

2.1.2 Product of Slice Functions and Their Zero Set

In general, the pointwise product of slice functions is not a slice function. However there is some product called “slice product” which does turn slice functions into slice functions.

The following notion is of great importance in the theory. For the following basic facts on this “slice product” see [23] and [22].

Definition 2.7

Let $f={\mathcal {I}}(F)$, $g={\mathcal {I}}(G)$ both belonging to ${\mathcal {S}}(\Omega _{D})$ then the slice product of f and g is the slice function

$$\begin{aligned} f* g:={\mathcal {I}}(FG)\in {\mathcal {S}}(\Omega _{D}). \end{aligned}$$

Explicitly, if $F=F_{1}+F_2\imath$ and $G=G_{1}+ G_{2}\imath$ are stem functions, then

$$\begin{aligned} FG=F_{1}G_{1}-F_{2}G_{2}+(F_{1}G_{2}+F_{2}G_{1})\imath . \end{aligned}$$

Definition 2.8

A slice function $f={\mathcal {I}}(F) \in {{\mathcal {S}}}(\Omega _D)$ is called slice preserving if, for all $J\in {\mathbb {S}}$, $f(\Omega _{D}\cap {\mathbb {C}}_{J})\subset {\mathbb {C}}_{J}$.

Slice-preserving functions satisfy the following characterization.

Proposition 2.9

Let $f={\mathcal {I}}(F_{1}+F_2\imath )$ be a slice function. Then f is slice preserving if and only if the ${{\mathbb {H}}}$-valued components $F_{1}$, $F_{2}$ are real valued.

Since real numbers commute with all quaternions, this has the following consequence:

Let $f, g\in {\mathcal {S}}(\Omega _{D})$. If f is slice preserving, then

$$\begin{aligned} (f*g)(x)=f(x)g(x). \end{aligned}$$

If f and g are both slice preserving, then $fg=f*g=g*f=gf$.

As stated in [22], if f is a regular function defined on ${\mathbb {B}}_{\rho }$, the ball of center 0, and radius $\rho ,$ then it is slice preserving if and only if f can be expressed as a power series of the form

$$\begin{aligned} f(x)=\sum _{n\in {\mathbb {N}}}x^{n}a_{n}, \end{aligned}$$

with $a_{n}$ real numbers.

The following definitions are taken from [22, 23].

Definition 2.10

Let $f={\mathcal {I}}(F)\in {\mathcal {S}}(\Omega _{D})$, then also $F^{c}(z)=F(z)^{c}:=F_{1}(z)^{c}+F_2(z)^{c}\imath$ is a stem function. We set

• $f^{c}:={\mathcal {I}}(F^{c})\in {\mathcal {S}}(\Omega _{D})$, the slice conjugate of f;

• $f^{s}:=f^c* f$, the symmetrization of f.

Remark 2.11

We have that $(FG)^{c}=G^{c}F^{c}$, and so $(f* g)^{c}=g^{c}* f^{c}$. In particular, $f^{s}=(f^{s})^{c}$. Moreover it holds

$$\begin{aligned} (f* g)^{s}=(f)^{s}(g)^{s}\quad \text{ and } \quad (f^{c})^{s}= f^{s}. \end{aligned}$$

Another observation is that, if f is slice preserving, then $f^{c}=f$ and so $f^{s}=f^{2}$.

Frequently, the sum $f+f^c$ is denoted by Tr(f).

2.1.3 Zeros of Regular Functions

We are going now to recall some key facts about the zeros of a slice function.

Let $f:\Omega _{D}\rightarrow {{\mathbb {H}}}$ be any slice function with zero locus

$$\begin{aligned} {\mathcal {Z}}(f) = \{ x\in \Omega _D : f(x)=0 \}. \end{aligned}$$

Let $x\in {\mathcal {Z}}(f)$. There are the following three possibilities:

• $x\in {\mathbb {R}}$, i.e., x is a real zero;

• x a punctual (non-real) zero, i.e., $x\notin {\mathbb {R}}$ and ${\mathbb {S}}_{x}\cap {\mathcal {Z}}(f)=\{x\}$;

• x a spherical zero, i.e., $x\notin {\mathbb {R}}$ and ${\mathbb {S}}_{x}\subset {\mathcal {Z}}(f)$.

The inclusion

$$\begin{aligned} {\mathcal {Z}}(f)\subset {\mathcal {Z}}(f*g), \end{aligned}$$

(5)

holds for any two slice functions $f,g:\Omega _{D}\rightarrow {{\mathbb {H}}}$, while in general ${\mathcal {Z}}(g)\not \subset {\mathcal {Z}}(f*g)$.

What is true in general is the following equality:

$$\begin{aligned} \bigcup _{x\in {\mathcal {Z}}(f* g)} {\mathbb {S}}_{x}=\bigcup _{x\in {\mathcal {Z}}(f)\cup {\mathcal {Z}}(g)}{\mathbb {S}}_{x} \end{aligned}$$

Theorem 2.12

[22] Let $f\in {{\mathcal {S}}}{{\mathcal {R}}}(\Omega _{D})$. If ${\mathbb {S}}_{x}\subset \Omega _{D}$ then the zeros of $f^{c}$ on ${\mathbb {S}}_{x}$ are in bijective correspondence with those of f. Moreover $f^{s}$ vanishes exactly on the sets ${\mathbb {S}}_{x}$ on which f has a zero.

2.1.4 Identity Principle

Theorem 2.13

(Identity principle, [20, 21]) Let $\Omega _D$ be a slice domain. Given $f={\mathcal {I}}(F):\Omega _{D}\rightarrow {{\mathbb {H}}}$ a regular function, if there exists a $J\in {\mathbb {S}}$ such that $(\Omega _{D}\cap {\mathbb {C}}_{J})\cap {\mathcal {Z}}(f)$ admits an accumulation point, then $f\equiv 0$ on $\Omega _{D}$.

Corollary 2.14

Let f be a regular function on a circular slice domain $\Omega _D$.

If there exists a convergent sequence of distinct numbers $p_n=x_n+iy_n$ in D such that f has at least one zero on every sphere of the form

$$\begin{aligned} \Sigma _n=\{ x_n+Iy_n: I\in {\mathbb {S}}\}, \end{aligned}$$

then f vanishes identically.

Proof

Under the assumptions of the corollary, the symmetrization $f^s=f^c*f$ vanishes identically on each $\Sigma _n$. Hence $(\Omega _{D}\cap {\mathbb {C}}_{J})\cap {\mathcal {Z}}(f^s)$ contains an accumulation point for any $J\in {\mathbb {S}}$. Consequently f must vanish identically. $\square$

2.1.5 Multiplicities of Zeros

Let $f\in {{\mathcal {S}}}{{\mathcal {R}}}(\Omega _D)$ such that $f^{s}$ does not vanish identically. Given $n\in {\mathbb {N}}$ and $q \in {\mathcal {Z}}(f)$, we say that x is a zero of f of total multiplicity n, and we will denote it by $m_f(x )=n$, if $((q-x )^{s})^n\mid f^{s}$ and $((x-q )^{s})^{n+1}\not \mid f^{s}$. If $m_f(x )=1$, then x is called a simple zero of f.

Lemma 2.15

Let f be a regular function on a circular domain with $f(p)=0$. Then there exists ${\tilde{p}}\in {\mathbb {S}}_p$ and a regular function g such that $f(q)=g(q)*(q-{\tilde{p}})$.

Proof

There is an element $a\in {\mathbb {S}}_p$ such that $f^c(a)=0$, implying that there exists a regular function h with $f^c(q)=(q-a)*h(q)$. It follows that $f(q)=h^c(q)*(q-a^c)$. $\square$

2.1.6 Semi-regular Functions and Their Poles

We will recall now some concept of “semi-regular functions” which are the quaternionic analog of meromorphic functions. Here our main references are [22] and [27].

Definition 2.16

Let $f={\mathcal {I}}(F)\in {{\mathcal {S}}}{{\mathcal {R}}}(\Omega _{D})$. We call the slice reciprocal of f the slice function

$$\begin{aligned} f^{-*}:\Omega _{D}\setminus {\mathcal {Z}}(f^{s})\rightarrow {\mathbb {H}}, \qquad f^{-*}={\mathcal {I}}((F^cF)^{-1}F^c). \end{aligned}$$

From the previous definition it follows that, if $x\in \Omega _D\setminus {\mathcal {Z}}(f^{s})$, then

$$\begin{aligned} f^{-*}(x)=(f^{s}(x))^{-1}f^{c}(x). \end{aligned}$$

The regularity of $f^{-*}$ on $\Omega _{D}\setminus {\mathcal {Z}}(f^{s})$ just defined follows thanks to the last equality.

If f is slice preserving, then $f^{c}=f$ and so $f^{-*}=f^{-1}$ where it is defined. Moreover $(f^{c})^{-*}=(f^{-*})^{c}$.

Proposition 2.17

Let $f\in {{\mathcal {S}}}{{\mathcal {R}}}(\Omega _{D})$ such that ${\mathcal {Z}}(f)=\emptyset$, then $f^{-*}\in {{\mathcal {S}}}{{\mathcal {R}}}(\Omega _{D})$ and

$$\begin{aligned} f* f^{-*}=f^{-*}* f=1. \end{aligned}$$

The concept of a semi-regular function has been introduced in [27, pp. 11.1–11.2]. For our purposes the crucial property of semi-regular functions is that every semi-regular function f may locally be written in the form $F=g^{-*}*h$ with g, h being slice regular functions.

Lemma 2.18

Let f be a slice function, $x,y\in {\mathbb {R}}$, $I,J\in {\mathbb {S}}$.

Then

$$\begin{aligned} f(x+yI)+f(x-yI)= f(x+yJ)+f(x-yJ) \end{aligned}$$

Proof

Due to the representation formula we have

$$\begin{aligned} f(x+yJ)=\frac{1-JI}{2}f(x+yI)+ \frac{1+JI}{2}f(x-yI) \end{aligned}$$

and

$$\begin{aligned} f(x-yJ)=\frac{1+JI}{2}f(x+yI)+ \frac{1-JI}{2}f(x-yI) \end{aligned}$$

Adding both above equalities yields the assertion of the lemma. $\square$

3 Divisors

In complex analysis, the divisor of a holomorphic function is the formal sum of its zeroes, counted with the respective multiplicities. We propose that for a quaternionic slice regular function defined on $\Omega _D$ the divisor should be defined as a formal sum of points in the closed upper plane intersected with D, i.e., on $\{z\in D:\mathfrak {I}(z)\ge 0\}$.

Definition 3.1

Let $\Omega _D$ be a slice domain and let f be a slice regular function on $\Omega _D$. Let $D^+=D\cap \{ z\in {{\mathbb {C}}}: \mathfrak {I}(z)\ge 0\}$.

Then the “(slice) divisor” div(f) of f is defined as the formal ${{\mathbb {Z}}}$-linear combination $\sum _{z\in D^+} m_z(f)\{z\}$ where for $z=x+yi$ the multiplicity $m_z(f)$ is defined as follows: $m_z(f)=m$ if in a neighborhood of ${\mathbb {S}}_{x+yI}= \{x+yJ:J\in {\mathbb {S}}\}$ the function f can be written as

$$\begin{aligned} f(q)=(q-a_1)*\ldots *(q-a_m)*g(q) \end{aligned}$$

with $a_i\in {\mathbb {S}}_{x+yI}$ and g being a slice regular function without zeros on ${\mathbb {S}}_{x+yI}$.

Standard facts on zeros of slice regular functions (see 2.1.3) guarantee us the following properties:

• $div(f*g)=div(f)+div(g)$ if both f and g are slice regular on $\Omega _D$.

• If $p_k=a_k+I_kb_k$ (with $a_k,b_k\in {{\mathbb {R}}}, b_k\ge 0, I_k\in {\mathbb {S}}$) are the isolated zeros with multiplicity $n_k$ and ${\mathbb {S}}_{c_k+Jd_k}$ are the spherical zeros with multiplicity $m_k$, then

  $$\begin{aligned} div(f) = \sum _k n_k\{a_k+ib_k\} +2 m_k\{c_k+id_k\} \end{aligned}$$

• $\{z\in D^+: div(f)>0\}$ is discrete in $D^+$ (for $f\not \equiv 0$).

For example, let $I,J\in {\mathbb {S}}$ with $I\ne J$ and consider $f(q)=(q-I)*(q-J)=q^2-q(I+J)+IJ$. Then f has a zero only at I while $g(q)=(q-J)*(q-I)$ has a zero only at J, but the divisor is the same:

$$\begin{aligned} div(f)=div(q-I)+div(q-J)=div(g)=2\{i\}. \end{aligned}$$

This notion of a divisor is easily extended from (slice) regular to semi-regular functions, since semi-regular functions may locally be written in the form $f=g^{-*}h$ with g, h slice regular. If $z=x+yi$ is a point in a symmetric domain D, and f is semi-regular on $\Omega _D$ we choose a sufficiently small symmetric domain $D'$ with $p\in D'\subset D$ such that f may be written in the form $g^{-*}*h$ on $\Omega _{D'}$. Then we define $div(f)=div(h)-div(g)$ on $D'$.

Warning

In complex analysis, a meromorphic function f is holomorphic iff $div(f)\ge 0$. The analog quaternionic statement is not true. For example, let $I,J\in {\mathbb {S}}$ and consider

$$\begin{aligned} (q-I)*(q-J)\frac{1}{q^2+1}= (q^2-q(I+J)+IJ)\frac{1}{q^2+1} \end{aligned}$$

This is a semi-regular function whose divisor is zero, although f is not slice regular unless $I=-J$.

4 A Mean Value Theorem

Proposition 4.1

(General mean value formula) Let $\mu$ be a probability measure on ${\mathbb {S}}$ which is invariant under $J\mapsto -J$.

Let f be a slice regular function on a slice domain $\Omega _D$ induced by a stem function $F:D\rightarrow {{\mathbb {H}}}\otimes {{\mathbb {C}}}$. Let $a,b,r\in {{\mathbb {R}}}$, $b\ge 0$, $r>0$, and $I\in {\mathbb {S}}$ such that $\Omega _D$ contains the closed ball with radius r and center $a+bI$.

Then we have:

$$\begin{aligned} F_1(a+bi)&=\frac{1}{4\pi } \int _{\mathbb {S}}\int _0^{2\pi } f(a+bJ+re^{J\theta })+f(a-bJ+re^{-J\theta }) \mathrm{{d}}\theta \mathrm{{d}}\mu (J)\\&=\frac{1}{2\pi } \int _{\mathbb {S}}\int _0^{2\pi } f(a+bJ+re^{J\theta }) \mathrm{{d}}\theta \mathrm{{d}}\mu (J) \end{aligned}$$

as well as

$$\begin{aligned} F_2(a+bi)= -\frac{1}{2\pi } \int _{\mathbb {S}}J \int _0^{2\pi } f(a+bJ+re^{J\theta })) \mathrm{{d}}\theta \mathrm{{d}}\mu (J) \end{aligned}$$

and therefore

$$\begin{aligned} f(a+bI)&= F_1(a+bi)+IF_2(a+bi)\\&=\frac{1}{2\pi } \int _{\mathbb {S}}\int _0^{2\pi } (1-IJ)f(a+bJ+re^{J\theta }) \mathrm{{d}}\theta \mathrm{{d}}\mu (J)\\ \end{aligned}$$

Proof

This follows from combining the complex mean value theorem with the formulae relating slice and stem functions. $\square$

Corollary 4.2

Let f be a regular function, $r>0$, $a\in {{\mathbb {R}}}$

Then

$$\begin{aligned} f(a)=\frac{1}{2\pi }\int _{{\mathbb {S}}}\int _0^{2\pi } f(a+r\cos \theta +r\sin \theta I) \mathrm{{d}}\theta \mathrm{{d}}\mu (I) \end{aligned}$$

for any probability measure $\mu$ on ${\mathbb {S}}$ which is invariant under the involution $J\mapsto -J$.

Proof

This a special case of Proposition 4.1 with $b=0$. $\square$

Remark 4.3

Note that in Corollary 4.2 we integrate over the sphere with radius r and center a, but not with respect to the euclidean volume element dV on the 3-sphere.

This is crucial.

For example, $\int _{||q||=1} q^2dV<0$, hence $\int _{||q||=1} f(q)dV\ne f(0)$ for $f(q)=q^2$.

4.1 Characterization of Harmonicity

A continuous function on ${{\mathbb {C}}}$ is harmonic if and only if it satisfies the mean value property.

We derive a similar criterion in the quaternionic setup.

Theorem 4.4

Let $\mu$ be a probability measure on ${\mathbb {S}}$ which is invariant under the involution $J\mapsto -J$. Let $f:{{\mathbb {H}}}\rightarrow {{\mathbb {H}}}$ be a continuous function and for $p=a+bI\in {{\mathbb {H}}}$ and $r>0$ define

$$\begin{aligned} M_{p,r}= \frac{1}{2\pi } \int _{\mathbb {S}}\int _0^{2\pi } (1-IJ)f(a+bJ+re^{J\theta }) \mathrm{{d}}\theta \mathrm{{d}}\mu (J). \end{aligned}$$

Then f is harmonic (in the sense of being the sum of a regular and an anti-regular function) if and only if

$$\begin{aligned} M_{p,r}=f(p)\quad \quad \forall p\in {{\mathbb {H}}}, r>0. \end{aligned}$$

(6)

Proof

We assume that (6) holds.

The function f is a slice function if and only if it satisfies the representation formula. Hence f is a slice function iff

$$\begin{aligned} f(a+bH)=\frac{1-HI}{2} M_{p,r}+\frac{1+HI}{2} M_{p^c,r} \end{aligned}$$

for all $a,b\in {{\mathbb {R}}}$, $H,I\in {\mathbb {S}}$, and $p=a+bI$.

This can be verified by explicit calculation:

$$\begin{aligned}&\frac{1-HI}{2} M_{p,r}+\frac{1+HI}{2} M_{p^c,r}\\&\quad = \frac{1}{4\pi } \int _{\mathbb {S}}\int _0^{2\pi } \left( (1-HI)(1-IJ)+(1+HI)(1+IJ)\right) f(a+bJ+re^{J\theta })\mathrm{{d}}\theta \mathrm{{d}}\mu (J)\\&\quad = \frac{1}{2\pi } \int _{\mathbb {S}}\int _0^{2\pi } \left( 1-HJ \right) f(a+bJ+re^{J\theta })\mathrm{{d}}\theta \mathrm{{d}}\mu (J)\\&\quad = M_{a+bH,r}=f(a+bH). \end{aligned}$$

Thus f is a slice function induced by some stem function F. This stem function can be easily determined as $F=F_1+F_2\otimes i$ with

$$\begin{aligned} F_1(a+bi)&= \frac{1}{2\pi } \int _{\mathbb {S}}\int _0^{2\pi } f(a+bJ+re^{J\theta })\mathrm{{d}}\theta \mathrm{{d}}\mu (J)\\ F_2(a+bi)&= - \frac{1}{2\pi } \int _{\mathbb {S}}\int _0^{2\pi } Jf(a+bJ+re^{J\theta })\mathrm{{d}}\theta \mathrm{{d}}\mu (J) \end{aligned}$$

Since $\mu$ is invariant under $J\mapsto -J$, we have

$$\begin{aligned} F_1(a+bi)&= \frac{1}{4\pi } \int _{\mathbb {S}}\int _0^{2\pi } f(a+bJ+re^{J\theta }) + f(a-bJ+re^{-J\theta }) \mathrm{{d}}\theta \mathrm{{d}}\mu (J)\\&= \frac{1}{2\pi }\int _0^{2\pi } F_1(a+bi+re^{i\theta }) \mathrm{{d}} \theta . \end{aligned}$$

Thus $F_1$ satisfies the ordinary mean value property for functions defined on ${{\mathbb {C}}}$ and therefore must be harmonic. Similar arguments apply to $F_2$. As a result we see that F is the sum of a holomorphic and an anti-holomorphic function from ${{\mathbb {C}}}$ to ${{\mathbb {H}}}\otimes _{{{\mathbb {R}}}}{{\mathbb {C}}}$ and consequently $f:{{\mathbb {H}}}\rightarrow {{\mathbb {H}}}$ is the sum of a regular and an anti-regular function.

For the opposite direction, assume that f is the sum of a regular function and an anti-regular function. Then (6) follows immediately from Proposition 4.1. $\square$

5 Generalized Representation Formula

For slice regular functions, the formula below already appeared in [15]: see Theorem 3.2. Here we give a new proof and we deduce some consequences.

Proposition 5.1

Let f be a slice function (not necessarily regular) and let $I,J,H\in {\mathbb {S}}$ (not necessarily orthogonal). Assume that $J\ne I$, $H\ne I$. Then the following equality holds:

$$\begin{aligned}&\left( \frac{1+JI}{2} \right) ^{-1} f(x+yJ) - \left( \frac{1+HI}{2}\right) ^{-1}f(x+yH) \\&\quad = \left( \left( \frac{1+JI}{2} \right) ^{-1} \left( \frac{1-JI}{2} \right) - \left( \frac{1+HI}{2}\right) ^{-1} \left( \frac{1-HI}{2}\right) \right) f(x+yI) \end{aligned}$$

Proof

We have

$$\begin{aligned} f(x+yJ)=\frac{1-JI}{2}f(x+yI)+ \frac{1+JI}{2}f(x-yI) \end{aligned}$$

and

$$\begin{aligned} f(x+yH)=\frac{1-HI}{2}f(x+yI)+ \frac{1+HI}{2}f(x-yI). \end{aligned}$$

A linear combination of both equations yields

$$\begin{aligned}&\left( \frac{1+HI}{2}\right) \left( \frac{1+JI}{2} \right) ^{-1} f(x+yJ) - f(x+yH) \\&\quad = \left( \left( \frac{1+HI}{2}\right) \left( \frac{1+JI}{2} \right) ^{-1} \left( \frac{1-JI}{2} \right) - \left( \frac{1-HI}{2}\right) \right) f(x+yI) \end{aligned}$$

and

$$\begin{aligned}&\left( \frac{1+JI}{2} \right) ^{-1} f(x+yJ) - \left( \frac{1+HI}{2}\right) ^{-1}f(x+yH) \\&\quad = \left( \left( \frac{1+JI}{2} \right) ^{-1} \left( \frac{1-JI}{2} \right) - \left( \frac{1+HI}{2}\right) ^{-1} \left( \frac{1-HI}{2}\right) \right) f(x+yI) \end{aligned}$$

$\square$

Lemma 5.2

Fix $I\in {\mathbb {S}}$. For $J\ne I$ we define

$$\begin{aligned} R(J)=\left( \frac{1+JI}{2} \right) ^{-1} \left( \frac{1-JI}{2} \right) \end{aligned}$$

Then $R:{\mathbb {S}}\setminus \{I\}\rightarrow {{\mathbb {H}}}$ is injective, and $R(J)=0$ iff $J=-I$.

Furthermore $\lim _{J\rightarrow I}|R(J)| = +\infty$.

Proof

Since I, J are purely imaginary, we have ${\overline{JI}}=IJ$. Therefore

$$\begin{aligned} \left( \frac{1+JI}{2} \right) ^{-1}=2\frac{1+IJ}{|1+JI|^2} \end{aligned}$$

and therefore

$$\begin{aligned} R(J)= \frac{(1+IJ)(1-JI)}{|1+JI|^2} =\frac{IJ-JI}{|1+JI|^2} \end{aligned}$$

Since ${\overline{IJ}}=JI$, $\frac{IJ-JI}{2}=\frac{IJ-{\overline{IJ}}}{2}$ denotes the vector part of IJ. Define $r=\mathfrak {R}\, (IJ)$. Observe that $r\in ]-1,+1]$. Using $|IJ|=1$ we know that the vector part of IJ has norm $\sqrt{1-r^2}$. Therefore

$$\begin{aligned} |R(J)|^2= 4\frac{1-r^2}{|1+JI|^4} \end{aligned}$$

Now $|1+JI|^2=|1+\mathfrak {R}\, (JI)|^2+|\mathfrak {I}\, (JI)|^2$ and therefore $|1+JI|^4=(2+2r)^2$ implying

$$\begin{aligned} |R(J)|^2=4\frac{1-r^2}{(2+2r)^2}=\frac{(1+r)(1-r)}{(1+r)^2} =\frac{1-r}{(1+r)}=\left( -1 +\frac{2}{1+r}\right) . \end{aligned}$$

We observe that the map

$$\begin{aligned} r\mapsto \left( -1 +\frac{2}{1+r}\right) \end{aligned}$$

is evidently an injective map from $(-1, +1]$ to ${\mathbb {R}}^+$.

As a consequence, we obtain: If $|R(J)|=|R(H)|$ for some $J,H\in {\mathbb {S}}\setminus \{ I \}$, then $\mathfrak {R}\, (IJ)=\mathfrak {R}\, (HI)$. On the other hand, the vector part of IJ equals

$$\begin{aligned} \frac{1}{2}\left( IJ-{\overline{IJ}}\right) =\frac{1}{2} R(J) |1+JI|^2 = R(J) (1+r) \end{aligned}$$

because $|1+JI|^2=(2+2r).$ Hence also the vector parts of JI and HI have to agree as soon as $R(J)=R(H)$. Finally observe that $J=H$ if $JI=HI$. $\square$

Proposition 5.3

Fix $I\in {\mathbb {S}}$. Then there exists a continuous map $M=(M_1,M_2):{\mathbb {S}}\times {\mathbb {S}}\setminus D_{\mathbb {S}}\rightarrow {{\mathbb {H}}}\times {{\mathbb {H}}}$ (where $D_{\mathbb {S}}$ denotes the diagonal, i.e., $D_{\mathbb {S}}=\{(q,q):q\in {\mathbb {S}}\}$) such that

$$\begin{aligned} f(x+yI)=M_1(J,H)f(x+yJ) + M_2(J,H) f(x+yH) \ \forall J,H\in {\mathbb {S}}\end{aligned}$$

(7)

for every regular function f.

Proof

First assume that I, J, H are pairwise distinct.

Then the statement follows from Proposition 5.1 with

$$\begin{aligned} M_1(J,H)=\left( R(J)-R(H) \right) ^{-1} \left( \frac{1+JI}{2} \right) ^{-1} \end{aligned}$$

and

$$\begin{aligned} M_2(J,H)=- \left( R(J)-R(H) \right) ^{-1} \left( \frac{1+HI}{2} \right) ^{-1}. \end{aligned}$$

(Note that $1+JI\ne 0$, resp. $1+HI\ne 0$, because of our assumptions $J\ne I$, $H\ne I$. Note further that $R(J)-R(H)\ne 0$ due to $J\ne H$ and the injectivity statement of Lemma 5.2.)

Next we claim that the functions $M_i$ do extend continuously to the points where $J=I$ or $H=I$, i.e., extend continuously to all of ${\mathbb {S}}\times {\mathbb {S}}\setminus D_{\mathbb {S}}$.

Consider the case where J approaches I. Since we excluded the diagonal $D_{\mathbb {S}}$, we may fix $H\ne I$.

Now

$$\begin{aligned} M_1(J,H)= & {} \left( R(J)-R(H) \right) ^{-1} \left( \frac{1+JI}{2} \right) ^{-1}\\= & {} \left( \frac{1+JI}{2} \left( R(J)-R(H) \right) \right) ^{-1}\\= & {} \left( \frac{1+JI}{2} R(J) - \frac{1+JI}{2}R(H) \right) ^{-1}\\= & {} \left( \frac{1-JI}{2} - \frac{1+JI}{2}R(H) \right) ^{-1} \end{aligned}$$

implying

$$\begin{aligned} \lim _{J\rightarrow I} M_1(J,H) = \left( \frac{2}{2} - 0\cdot R(H) \right) ^{-1} =1 \end{aligned}$$

In a similar way one proves

$$\begin{aligned} \lim _{J\rightarrow I} M_2(J,H)=0 \end{aligned}$$

and the analog statement for $H\rightarrow I$. $\square$

Remark 5.4

We observe that our formula (7) coincides with the Representation Formula of Proposition 6 in [23], when $M_1(J,H)=(I-H)(J-H)^{-1}$ and $M_2(J,H)=-(I-J)(J-H)^{-1}.$

6 Rotations

For every $w\in {{\mathbb {H}}}^*$ let $S_w:{{\mathbb {H}}}\rightarrow {{\mathbb {H}}}$ denote the map given by $S_w(q)=w^{-1}qw$. This is an orthogonal transformation of ${\mathbb {R}}^4$ which fixes ${\mathbb {R}}$ pointwise. Observe that $S_w^{-1}=S_{w^{-1}}$.

Lemma 6.1

Let I, J, K be orthogonal imaginary units.

Then $S_I:{{\mathbb {H}}}\rightarrow {{\mathbb {H}}}$ is a linear map acting as id on ${{\mathbb {C}}}_I=\left<1,I\right>_{\mathbb {R}}$ and as $-id$ on ${{\mathbb {C}}}_I^\perp = \left<J,K\right>_{\mathbb {R}}$.

Proof

Follows easily from explicit calculations. $\square$

The following lemma is a well-known result, see for example [28] Prop. 2.22, page 28), but for the reader convenience we prefer to give here our own proof.

Lemma 6.2

The group of all orientation preserving orthogonal transformations of $\left<I,J,K\right>_{\mathbb {R}}$ is generated by the transformations $S_w$ with $w\in {\mathbb {S}}$.

Proof

The group is $SO(3,{\mathbb {R}})$. For each $k\in {{\mathbb {N}}},$ let $\Sigma _k$ denote the set of all $S_{w_1}\circ \ldots \circ S_{w_{2k}}$. Then $\Sigma =\cup _k\Sigma _k$ is the group generated by all the $S_w$. ($\Sigma$ is evidently a semigroup and in fact a group, because $(S_w)^{-1}=S_{w^{-1}}$.) $\Sigma$ is connected, because each $\Sigma _k$ is connected and $\Sigma _{k} \subseteq \Sigma _{k+1}.$ On the other hand, it is not commutative, since e.g., $S_I$ and $S_{(I+J)/\sqrt{2}}$ do not commute. However, by standard Lie theory, $SO(3,{\mathbb {R}})$ has no non-commutative connected subgroups except $SO(3,{\mathbb {R}})$ itself. $\square$

Lemma 6.3

Let $q\in {{\mathbb {H}}}$. Let $\mu$ denote the (unique) probability measure on ${\mathbb {S}}$ which is invariant under all rotations.

Then

$$\begin{aligned} \mathfrak {R}\, (q)=\int _{{\mathbb {S}}} S_w(q)\mathrm{{d}}\mu (w) \end{aligned}$$

Proof

The map $H:q\mapsto \int _{{\mathbb {S}}} S_w(q)\mathrm{{d}}\mu (w)$ is ${{\mathbb {R}}}$-linear.

Let $v\in {\mathbb {S}}$. Then $S_v$ is an orthogonal transformation. Due to the invariance of the measure $\mu$, we have

$$\begin{aligned} S_v(H(q)) =\int _{{\mathbb {S}}} S_v\left( S_w(q)\right) \mathrm{{d}}\mu (w) =\int _{{\mathbb {S}}} S_w(q) S_v^*\mathrm{{d}}\mu (w)=\int _{{\mathbb {S}}} S_w(q)\mathrm{{d}}\mu (w)=H(q). \end{aligned}$$

(Here $S_v^*$ denotes the pull-back by the map $S_v$.)

It follows that

$$\begin{aligned} H(q)\in \{x\in {{\mathbb {H}}}:S_w(x)=x ,\,\, \forall w \in {\mathbb {S}} \}={{\mathbb {R}}}\, , \,\, \forall q\in {{\mathbb {H}}}. \end{aligned}$$

We observe that $\int _{{\mathbb {S}}} S_w(q)\mathrm{{d}}\mu (w)=q, \,\, \forall q\in {{\mathbb {R}}}$, because $S_w(q)=q, \,\, \forall q\in {{\mathbb {R}}}, w\in {\mathbb {S}}$.

Now let q be in the orthogonal complement of ${{\mathbb {R}}}$, i.e., in the real vector subspace V of ${{\mathbb {H}}}$ spanned by I, J, K. Since the integral is linear, and V is stabilized by every $S_w$ ($w\in {\mathbb {S}}$) it follows that

$$\begin{aligned} H(q)=\int _{{\mathbb {S}}} S_w(q)\mathrm{{d}}\mu (w)\in V , \,\,\, \forall q\in V. \end{aligned}$$

Combined with the fact $H(q)\in {{\mathbb {R}}}, \,\, \forall q\in {{\mathbb {H}}}$, we obtain

$$\begin{aligned} H(q)=\int _{{\mathbb {S}}} S_w(q)\mathrm{{d}}\mu (w)\in V\cap {{\mathbb {R}}}=\{0\}, \,\,\, \forall q\in V. \end{aligned}$$

Thus

$$\begin{aligned} \mathfrak {R}\, (q)=\int _{{\mathbb {S}}} S_w(q)\mathrm{{d}}\mu (w) \end{aligned}$$

for every $q\in {{\mathbb {R}}}$ and every $q\in V$. By ${{\mathbb {R}}}$-linearity of the map H, it follows that this equality holds for all $q\in {{\mathbb {H}}}$. $\square$

Definition 6.4

A function $f:{{\mathbb {H}}}\rightarrow {{\mathbb {H}}}$ is called “rotationally invariant” if it is invariant under all orthogonal transformations of the space of imaginary elements.

Remark 6.5

This class of functions has been studied in [26] where they are called “circular” functions.

Lemma 6.6

For a function $f:{{\mathbb {H}}}\rightarrow {{\mathbb {H}}}$ the following properties are equivalent:

• (1) f is rotationally invariant.

• (2) $f(q)=f(S_wq)$ for all $q\in {{\mathbb {H}}}$, $w\in {\mathbb {S}}$.

• (3) $f(x+yI)=f(x+yJ)$ for all $x,y\in {{\mathbb {R}}}$, $I,J\in {\mathbb {S}}$.

• (4) f is induced by a stem function F with $F({{\mathbb {C}}})\subset {{\mathbb {H}}}\otimes {{\mathbb {R}}}$, i.e., $F_2=0$ for $F=F_1+F_2\imath$.

Proof

First we show $(3)\Rightarrow (4)$: Given such a function f, we define $F:{{\mathbb {C}}}\rightarrow {{\mathbb {H}}}\otimes {{\mathbb {C}}}$ as $F(x+iy)=f(x+yI)\otimes 1$ for any $I\in {\mathbb {S}}$. Since (3) implies $f(x+yI)=f(x+y(-I))$, we have $F(z)=F({{\bar{z}}})$. Combined with $F({{\mathbb {C}}})\subset {{\mathbb {H}}}\otimes {{\mathbb {R}}}$ it follows that $\overline{F(z)}=F(z)=F({{\bar{z}}})$. Consequently F fulfills $F({{\bar{z}}})=\overline{F(z)}$ and is a stem function.

The implications $(4)\Rightarrow (3)\iff (1)\Rightarrow (2)$ are obvious. The implication $(2)\Rightarrow (1)$ follows from Lemma 6.2. $\square$

Definition 6.7

Let $\Omega$ be a circular¹ subset of ${{\mathbb {H}}}$ and let $f:\Omega \rightarrow {{\mathbb {H}}}$ be a function. Let $w\in {\mathbb {S}}$.

Then we define a function $R_wf:\Omega \rightarrow {{\mathbb {H}}}$ as

$$\begin{aligned} (R_wf)(q)=S_w^{-1}\left( f(S_w(q)\right) ). \end{aligned}$$

Lemma 6.8

Let $\Omega _D$ be a slice domain, and let $f:\Omega _D \rightarrow {{\mathbb {H}}}$ be a slice function induced by a stem function $F:D\rightarrow {{\mathbb {H}}}\otimes {\mathbb {C}}$.

Then $R_wf$ is induced by $S_{w^{-1}}(F)$ with $S_{w^{-1}}$ acting via the first factor of the tensor product ${{\mathbb {H}}}\otimes {\mathbb {C}}$.

Proof

We have

$$\begin{aligned} f(x+yI)=F_1(x+yi)+IF_2(x+yi)\ \ \ (x,y\in {\mathbb {R}}, I\in {\mathbb {S}}, x+yi\in D) \end{aligned}$$

and

$$\begin{aligned} R_wf(q)=w\left( f(w^{-1}qw) \right) w^{-1}. \end{aligned}$$

Now $w^{-1}qw=x+yw^{-1}Iw$ for $q=x+yI$. Furthermore $w^{-1}Iw\in {\mathbb {S}}$ and consequently

$$\begin{aligned} f(x+yw^{-1}Iw)= F_1(x+yi) +w^{-1}IwF_2(x+yi). \end{aligned}$$

Therefore

$$\begin{aligned} (R_wf)(x+yI)&= w\left( f\left( x+yw^{-1}Iw\right) \right) w^{-1}\\&= w\left( F_1(x+yi) +w^{-1}IwF_2(x+yi) \right) w^{-1}\\&= wF_1(x+iy)w^{-1}+IwF_2(x+yi)w^{-1} \end{aligned}$$

Therefore (using Lemma 2.3) $R_wf$ is induced by the stem function

$$\begin{aligned} S_{w^{-1}}F=\left( S_{w^{-1}}F_1\right) \otimes 1 + \left( S_{w^{-1}}F_2\right) \otimes i \end{aligned}$$

$\square$

Corollary 6.9

Let f denote a slice regular function on a slice domain $\Omega _D$ and let $w\in {\mathbb {S}}$.

Then $R_wf:\Omega _D\rightarrow {{\mathbb {H}}}$ is a slice regular function, too.

Proof

As a slice regular function, f is induced by a holomorphic stem function $F:D\rightarrow {{\mathbb {H}}}\otimes {{\mathbb {C}}}$. Holomorphicity of F implies that

$$\begin{aligned} z\mapsto \left( S_wF\right) (z)=w^{-1}(F(z))w \end{aligned}$$

is likewise holomorphic. Hence $R_wf$ is slice regular. $\square$

Corollary 6.10

Under the assumptions of the Lemma 6.8,

$$\begin{aligned} g=\int _{{\mathbb {S}}} R_w(f)\mathrm{{d}}\mu (w) \end{aligned}$$

is induced by the stem function R(F) where R denotes the real part in the first factor of the tensor product, i.e., $R(a\otimes b)=(\mathfrak {R}\, a)\otimes b$, for $a\in {{\mathbb {H}}}$, $b\in {{\mathbb {C}}}$.

Proof

By the Lemma 6.8, g is induced by $\int _{w} S_{w^{-1}}F\mathrm{{d}}\mu (w)$. Aided by Lemma 2.3, this implies the assertion, because

$$\begin{aligned} \int _{{\mathbb {S}}} S_{w^{-1}}(q)\mathrm{{d}}\mu (w)=\mathfrak {R}\, (q) \end{aligned}$$

for every $q\in {{\mathbb {H}}}$ (Lemma 6.3). $\square$

Lemma 6.11

Let f be a slice regular function given by a convergent power series $f=\sum _{k=0}^{+ \infty } q^ka_k$.

Then the following holds:

$$\begin{aligned} \int _{\mathbb {S}}R_wf\mathrm{{d}}\mu (w) =\sum _k q^k\mathfrak {R}\, (a_k)=\frac{1}{2}(f+f^c) = \frac{1}{2} Tr(f). \end{aligned}$$

We observe that $R_{vw}=R_v\circ R_w$ and $S_{vw}=S_w\circ S_v$ for $v,w\in {{\mathbb {H}}}^*$.

Definition 6.12

For $v\in {{\mathbb {H}}}$ let $\partial _v$ denote the directional derivative in the direction of v, i.e.,

$$\begin{aligned} (\partial _v)(f)(q)=\lim _{t\rightarrow 0, t\in {{\mathbb {R}}}^*}\frac{f(q+vt)-f(q)}{t}. \end{aligned}$$

Next we discuss differential operators $\partial _*$, ${{\bar{\partial }}}_*$ for differentiable functions on ${{\mathbb {H}}}\setminus {{\mathbb {R}}}$. These operators were first introduced by Ghiloni and Perotti in [25] as $\vartheta$ resp. ${\bar{\vartheta }}$. For slice functions, they coincide with the operators $\partial /\partial x$ and $\partial /\partial x^c$ introduced in [23].

Definition 6.13

Let $\Omega$ be a domain in ${{\mathbb {H}}}$ and let $f:\Omega \rightarrow {{\mathbb {H}}}$ be a $C^1$-function. Let $I\in {\mathbb {S}}$ and $q\in ({{\mathbb {C}}}_I\setminus {{\mathbb {R}}})\cap \Omega$.

We define

$$\begin{aligned} \left( \partial _*f\right) (q)&= \left( \frac{1}{2}\left( \partial _1-I\partial _I\right) f\right) (q)\\ \left( {{\bar{\partial }}}_*f\right) (q)&= \left( \frac{1}{2}\left( \partial _1+I\partial _I\right) f\right) (q). \end{aligned}$$

(with $\partial _1$, $\partial _I$ being directional derivatives, cf. 6.12).

Remark 6.14

Let $\Omega$ be a domain. Let I, J be orthogonal imaginary units, $f:\Omega \rightarrow {{\mathbb {H}}}$, $g,h:\Omega \rightarrow {{\mathbb {C}}}_I$ be $C^1$-functions with $f=g+hJ$.

Then ${{\bar{\partial }}}_* f$ vanishes on $\Omega \cap {{\mathbb {C}}}_I$ if and only if the restrictions of g, h are holomorphic functions from $\Omega \cap {{\mathbb {C}}}_I$ to ${{\mathbb {C}}}_I$.

Next we define a Laplacian:

Definition 6.15

Let $\Omega$ a domain in ${{\mathbb {H}}}$, f be a $C^2$-function on $\Omega$ and $q\in \Omega \setminus {{\mathbb {R}}}$.

We define

$$\begin{aligned} (\Delta _* f)(q)=\left( 4\partial _*{{\bar{\partial }}}_* f\right) (q). \end{aligned}$$

Remark 6.16

• (1) $\Delta _* = 4\partial _*{{\bar{\partial }}}_* = 4{{\bar{\partial }}}_*\partial _*$.

• (2) For orthogonal imaginary units $I,J\in {\mathbb {S}}$ the restriction of $\Delta _*f$ to $\Omega \cap {{\mathbb {C}}}_I$ vanishes if and only if $f|_{{{\mathbb {C}}}_I}=g+hJ$ with $g,h:{{\mathbb {C}}}_I\rightarrow {{\mathbb {C}}}_I$ harmonic in the sense of complex analysis.

Lemma 6.17

Let $I\in {\mathbb {S}}$. Then $\Delta _*(f)$ vanishes along ${\mathbb {C}}_I$ for (slice) regular functions f (and anti-regular functions f).

Proof

This is clear, because the restriction of a regular function f to a complex line ${{\mathbb {C}}}_I$ can be written as $f(z)=f_1(z)+f_2(z)J$ where $f_i:{{\mathbb {C}}}_I\rightarrow {{\mathbb {C}}}_I,$ for $i=1,2,$ are entire functions with respect to the complex structure on ${{\mathbb {C}}}_I$ and J orthogonal to I, by the splitting Lemma 2.6. $\square$

Let us now discuss the case where f is a slice function, i.e., induced by a stem function F.

Proposition 6.18

Let $\Omega _D$ be circular domain, arising as circularization of a symmetric domain D in ${{\mathbb {C}}}$.

Let $f:\Omega _D \rightarrow {{\mathbb {H}}}$ be a slice function which is induced by a stem function $F:D\rightarrow {{\mathbb {H}}}\otimes {\mathbb {C}}$. Then $\partial _* f$, ${{\bar{\partial }}}_*f$, and $\Delta _*f$ are slice functions on $\Omega _D\setminus {{\mathbb {R}}}$ induced by the stem functions $\frac{\partial F}{\partial z}$, $\frac{\partial F}{\partial {{\bar{z}}}}$ resp. $\Delta F$.

Proof

This may be deduced from the definitions of the respective operators using the representation formula for slice functions. See [25], Theorem 2.2. $\square$

In particular, for slice functions these operators $\partial _*$, ${{\bar{\partial }}}_*$, and $\Delta _*$ are well-defined everywhere, including at the real points, whereas for arbitrary $C^1$-functions they are defined only outside ${{\mathbb {R}}}$.

Corollary 6.19

A slice function f is annihilated by $\Delta _*$ if and only if its stem function F is harmonic.

Corollary 6.20

Let f be a $C^2$ slice function on a circular domain $\Omega _D$. If $\Delta _*f\equiv 0$, then f is real-analytic.

Corollary 6.21

Let $f:{{\mathbb {H}}}\rightarrow {{\mathbb {H}}}$ be a $C^2$ slice function. If f is bounded and $\Delta _*f$ vanishes identically, then f is constant.

Proof

$\Delta _*f\equiv 0$ implies the harmonicity of the stem function F. Now boundedness of f implies boundedness of F which leads to a contradiction unless F (and therefore also f) is constant. $\square$

Theorem 6.22

Let $\Omega _D$ be a slice domain. Let $f:\Omega _D\rightarrow {{\mathbb {H}}}$ be a $C^2$ slice function. Assume that D is simply connected.

• (1) $\Delta _*f$ is vanishing identically if and only if f can be written as a sum of a regular function g and an anti-regular function h.

• (2) Assume $\Delta _*f\equiv 0$. Let $D_{{\mathbb {R}}}=D\cap {{\mathbb {R}}}$. Then f can be written as a sum of a slice-preserving regular function g and a slice-preserving anti-regular function h if and only if

  $$\begin{aligned} f(x)\in {{\mathbb {R}}},\ \forall x\in D_{{\mathbb {R}}}\quad \text { and }(\partial _*f)(x)\in {{\mathbb {R}}}, \ \forall x\in D_{{\mathbb {R}}}, \end{aligned}$$

  which in turn holds if and only if

  $$\begin{aligned} f(x)\in {{\mathbb {R}}},\ \forall x\in D_{{\mathbb {R}}}\quad \text { and }({{\bar{\partial }}}_*f)(x)\in {{\mathbb {R}}}, \ \forall x\in D_{{\mathbb {R}}}, \end{aligned}$$

  or if and only if

  $$\begin{aligned}&\exists \,\, p\in D\cap {{\mathbb {R}}}:f(p)\in {{\mathbb {R}}}, ({{\bar{\partial }}}_*f)(x)\in {{\mathbb {R}}}, \ \forall x\in D_{{\mathbb {R}}}\\&\quad \text { and } (\partial _*f)(x)\in {{\mathbb {R}}}, \ \forall x\in D_{{\mathbb {R}}}. \end{aligned}$$

Proof

Let F be the stem function inducing f. Then $\Delta _*f$ is a slice function induced by the stem function $\Delta F$. Now F is a map from D to the complex vector space ${{\mathbb {H}}}\otimes {{\mathbb {C}}}$. Hence $\Delta F$ vanishes iff F is harmonic iff $F=G+H$ for a holomorphic function $G:D\rightarrow {{\mathbb {H}}}\otimes {{\mathbb {C}}}$ and an anti-holomorphic function $H:D\rightarrow {{\mathbb {H}}}\otimes {{\mathbb {C}}}$.

We have to verify that G, H may be taken to be stem functions. To state it more precisely, we have to show: If $F:D\rightarrow {{\mathbb {H}}}\otimes {{\mathbb {C}}}$ is a map such that $\overline{F({{\bar{z}}})} =F(z)$ and such that $F=G+H$ for a holomorphic map G and an anti-holomorphic map H, then G and H may be chosen in such a way that $\overline{G({{\bar{z}}})} =G(z)$ and $\overline{H({{\bar{z}}})} =H(z)$. Now $G(z)-\overline{G({{\bar{z}}})}$ is holomorphic, $H(z)-\overline{H({{\bar{z}}})}$ is anti-holomorphic, and

$$\begin{aligned} \left( G(z)-\overline{G({{\bar{z}}})} \right) + \left( H(z)-\overline{H({{\bar{z}}})} \right) =0 \end{aligned}$$

because of $F=G+H$ and $\overline{F({{\bar{z}}})} =F(z)$. It follows that there is a constant c such that

$$\begin{aligned} \left( G(z)-\overline{G({{\bar{z}}})} \right) =c= -\left( H(z)-\overline{H({{\bar{z}}})} \right) . \end{aligned}$$

We observe that c is totally imaginary and that

$$\begin{aligned} \overline{G({{\bar{z}}})-c/2}=\overline{G({{\bar{z}}})} +c/2= G(z) - c/2 \end{aligned}$$

Thus, by replacing G with $G- c/2$ we may turn G into a stem function. Correspondingly we replace H by $H+c/2$.

Finally we let g, resp. h, be the slice functions induced by the stem functions G, resp. H, and observe that g is regular, because G is holomorphic and h is anti-regular, because H is anti-holomorphic.

Now we demonstrate (2).

First we observe that

$$\begin{aligned} \partial _*f+{{\bar{\partial }}}_*f = \partial _1f \end{aligned}$$

Hence, if two of these values are zero, so is the third.

Next we claim:

$f(\Omega _D\cap {{\mathbb {R}}})\subset {{\mathbb {R}}}$ if and only if $(\partial _1f)$ is real on $\Omega _D\cap {{\mathbb {R}}}$ and $\exists \,\, p\in \Omega _D\cap {{\mathbb {R}}}$ such that $f(p)\in {{\mathbb {R}}}$.

The direction “$\implies$” is obvious. To verify the converse, let I denote a connected component ot $\Omega _D\cap {{\mathbb {R}}}$. Then $f(I)\subset {{\mathbb {R}}}$. This implies that the stem function F maps I into ${{\mathbb {R}}}\otimes {{\mathbb {C}}}\subset {{\mathbb {H}}}\otimes {{\mathbb {C}}}$. Because $F:D\rightarrow {{\mathbb {H}}}\otimes {{\mathbb {C}}}$ is a holomorphic map, we may now conclude with the identity principle that $F(D)\subset {{\mathbb {R}}}\otimes {{\mathbb {C}}}$. Using $\overline{F({{\bar{z}}})}=F(z)$, this implies that $F({{\mathbb {R}}}\cap D)\subset {{\mathbb {R}}}$ which in turn (via representation formula) implies $f({{\mathbb {R}}})\subset {{\mathbb {R}}}$.

This completes the proof, because a slice function f on a slice domain $\Omega _D$ is slice preserving if and only if the stem function F satisfies $F(D\cap {{\mathbb {R}}})\subset {{\mathbb {R}}}\otimes _{{\mathbb {R}}}{{\mathbb {R}}}\subset {{\mathbb {H}}}\otimes {{\mathbb {C}}}$. $\square$

Remark 6.23

We observe that in [29] a function in the kernel of $\Delta _*$ is called slice-harmonic.

Definition 6.24

$$\begin{aligned} (\Delta 'f)(q)=\left( \Delta _*\int _{{\mathbb {S}}}R_wf\mathrm{{d}}\mu (w)\right) (q) \end{aligned}$$

We observe that $(\Delta ' f)(q)=\frac{1}{2}\Delta _* (Tr(f))(q)=\frac{1}{2}\Delta _* (f+f^c)(q)$ for all $I \in {\mathbb {S}}.$

Analogously we can introduce another second-order operator in the following way:

$$\begin{aligned} (\Delta '' f)(q)=(\Delta _* N(f))(q)=(\Delta _* (f \cdot f^c)) (q) \end{aligned}$$

for all $I \in {\mathbb {S}}.$

On one side $\Delta '$ and $\Delta _*$ are linear operators, on the other hand, $\Delta ''$ is not a linear operator.

By the way, for $\Delta ''$ a product formula holds:

Proposition 6.25

Let f, g be slice functions. Then

$$\begin{aligned} \Delta ''(f*g)=(f^s)*\Delta '' g + (\Delta '' f) * (g^s) +\left( \partial _*(f^s)* {{\bar{\partial }}}_*(g^s) \right) +\left( {{\bar{\partial }}}_*(f^s)* \partial _*(g^s) \right) \end{aligned}$$

Proof

First we note that

$$\begin{aligned} \Delta ''(f*g)=\Delta _*(N(f*g))=\Delta _*((f*g)^s)= \Delta _*(f*g*g^c *f^c) \end{aligned}$$

Next we recall that (with respect to the slice product $*$) a slice-preserving function commutes with every other slice function. Since $g*g^c$ is always slice preserving, we obtain

$$\begin{aligned}&\Delta _*(f*g*g^c *f^c)=\Delta _*(f*f^{c}*g*g^c)\\&\quad = \Delta _*(f^s* g^s)=\partial _*{{\bar{\partial }}}_*(f^s\cdot g^s)\\&\quad = \partial _* \left( ({{\bar{\partial }}}_*f^s)\cdot g^s + f^s\cdot ({{\bar{\partial }}}_*g^s) \right) \\&\quad = (\partial _* {{\bar{\partial }}}_*f^s)\cdot g^s + ({{\bar{\partial }}}_*f^s)\cdot (\partial _* g^s) + (\partial _*f^s)\cdot ({{\bar{\partial }}}_*g^s) + f^s\cdot (\partial _*{{\bar{\partial }}}_*g^s) \\&\quad = f^s*(\Delta '' g) + (\Delta '' f) * g^s + ({{\bar{\partial }}}_*f^s)\cdot (\partial _* g^s) +(\partial _*f^s)\cdot ({{\bar{\partial }}}_*g^s)\\ \end{aligned}$$

$\square$

Remark 6.26

In [17] the following global first-order differential operator was introduced:

$$\begin{aligned} G(x)=(x_1^2 +x_2^2 + x_3^2) \frac{\partial }{\partial x_0} +(x_1 i +x_2 j + x_3 k) \cdot \sum _{j=1}^3 x_j \frac{\partial }{\partial x_j} \end{aligned}$$

where $x=x_0 + x_1 i + x_2 j + x_3 k.$ Direct calculations verify readily that $G=y^2{{\bar{\partial }}}_*$ where

$$\begin{aligned} y=|\mathfrak {I}(x)|= \sqrt{\sum _{k=1}^3|x_i|^2}. \end{aligned}$$

Whereas the operator $\Delta _*$ is defined everywhere only if applied to slice functions, G is everywhere defined for any $C^1$-function.

Still, we believe that the additional factor $y^2$ (which guarantees the applicability of the operator even to non-slice functions) is somewhat unnatural.

In particular, if we try to construct a second-order differential operator, we see that

$$\begin{aligned} {{\bar{G}}} G=y^4\Delta _* -2Iy^3{{\bar{\partial }}}_*. \end{aligned}$$

Thus ${{\bar{G}}} G$ even applied to slice functions on a complex slice ${{\mathbb {C}}}_I$ is not merely the multiple of the ordinary complex Laplacian. Moreover, ${{\bar{G}}}G$ annihilates regular functions, but not anti-regular functions.

We observe that in [25] a global operator related to G was studied.

Remark 6.27

It may happen that a function $f:{{\mathbb {H}}}\rightarrow {{\mathbb {H}}}$ satisfies both ${{\bar{\partial }}}_*Tr(f)=0$ and ${{\bar{\partial }}}_* N(f)=0$, but nevertheless is not regular. For example, let $I,J\in {\mathbb {S}}$ be orthogonal (i.e., $IJ=-JI$), and consider the function

$$\begin{aligned} f:q\mapsto I\cos (\mathfrak {R}q)+J\sin (\mathfrak {R}q). \end{aligned}$$

This is a slice function (induced by the stem function $z\mapsto I\otimes \cos (\mathfrak {R}z) + J\otimes \sin (\mathfrak {R}(z))$.) It is not regular because it is not open, although both $Tr(f)=f+f^c=0$ and $N(f)=ff^c=1$ are regular (in fact constant) functions.

Definition 6.28

A function $f:{{\mathbb {H}}}\rightarrow {{\mathbb {H}}}$ is rotationally equivariant if $R_I(f)=f$ for all $I\in {\mathbb {S}}$.²

Lemma 6.29

For a function $f:{{\mathbb {H}}}\rightarrow {{\mathbb {H}}}$, the following conditions are equivalent:

• (1) f is rotationally equivariant.

• (2) $R_I(f)=f$ for all $I\in {\mathbb {S}}$.

• (3) $S_I(f(q))=f(S_I(q))$ for all $I\in {\mathbb {S}}$ and $q\in {{\mathbb {H}}}$.

• (4) If $g:q\rightarrow g\cdot q$ denotes the ${{\mathbb {R}}}$-linear action of $SO(3,{{\mathbb {R}}})$ on ${{\mathbb {H}}}$ which is trivial on ${{\mathbb {R}}}$ and which is the natural orthogonal transformations on $\left<I,J,K\right>={{\mathbb {R}}}^3$, then $f:{{\mathbb {H}}}\rightarrow {{\mathbb {H}}}$ is equivariant for this action, i.e., $g\cdot f(q)=f(g\cdot q)$ for all $g\in SO(3,{{\mathbb {R}}})$, $q\in {{\mathbb {H}}}$.

• (5) f is induced by a stem function $F:{{\mathbb {C}}}\rightarrow {{\mathbb {H}}}\otimes {{\mathbb {C}}}$ with $F({{\mathbb {C}}})\subset {{\mathbb {R}}}\otimes {{\mathbb {C}}}$, i.e., both $F_1$ and $F_2$ are real valued for $F=F_1+ F_2\imath$.

• (6) f is induced by a stem function F and f is slice preserving, i.e., $f({{\mathbb {C}}}_I)\subset {{\mathbb {C}}}_I$, $\forall I\in {\mathbb {S}}$.

Proof

The equivalence $(5)\iff (6)$ is well known. $(1)\iff (2)\iff (3)$ follow directly from the respective definitions. Lemma 6.2 implies $(3)\iff (4)$. $(5)\Rightarrow (2)$ is easy. Finally, assume (3). Fix $I\in {\mathbb {S}}$. Then (3) implies $S_I(f(q))=f(S_I(q))$. For $q\in {{\mathbb {C}}}_I$ we have $S_I(q)=q$ and therefore $S_I(f(q))=f(q)$, which implies $f(q)\in {{\mathbb {C}}}_I$. Thus $f({{\mathbb {C}}}_I)\subset {{\mathbb {C}}}_I$. We define functions $g,h:{{\mathbb {C}}}\rightarrow {{\mathbb {R}}}$ such that

$$\begin{aligned} f(x+yI)=g(x+yi)+h(x+yi)I\ \ (x,y\in {{\mathbb {R}}}) \end{aligned}$$

Now, for every $J\in {\mathbb {S}}$, there is an orthogonal transformation $\phi$ fixing ${{\mathbb {R}}}$ with $\phi (I)=J$. Using (4), we have

$$\begin{aligned} f(x+yJ)&=f(\phi (x+yI))=\phi ( f(x+yI))\\&=\phi \left( g(x+yi)+h(x+yi)I\right) = g(x+yi)+h(x+yi)J \end{aligned}$$

Thus $f:{{\mathbb {H}}}\rightarrow {{\mathbb {H}}}$ is induced by the stem function F given as $F(x+yi)=g(x,y) \otimes 1 + h(x,y)\otimes i$. (The fact $\overline{F(z)}=F({{\bar{z}}})$ follows from Lemma 2.3.) This completes the proof of $(3)\Rightarrow (5)$. $\square$

Lemma 6.30

Let $h:{{\mathbb {H}}}\rightarrow {{\mathbb {R}}}$. Then the following conditions are equivalent:

• (1) h is induced by a stem function.

• (2) h obeys the representation formula.

• (3) h is rotationally equivariant.

• (4) h is rotationally invariant.

Moreover, in this case the stem function H can be defined as

$$\begin{aligned} H(x+yi)=h(x+yI)\otimes 1 \end{aligned}$$

for all $x,y\in {{\mathbb {R}}}$, $I\in {\mathbb {S}}$.

Proof

Assume that h is induced by a stem function H. The formula

$$\begin{aligned} h(x+yI)=F_1(x+yi) + I F_2(x+yi)\ \forall x,y\in {{\mathbb {R}}}, I\in {\mathbb {S}}\end{aligned}$$

combined with $h(q)\in {{\mathbb {R}}},\ \forall q\in {{\mathbb {H}}}$, implies that $F_2$ vanishes and that $F_1({{\mathbb {C}}})\subset {{\mathbb {R}}}$. Then h is rotationally equivariant (by Lemma 6.29$(5)\Rightarrow (1)$) and rotationally invariant (by Lemma 6.6$(5)\Rightarrow (1)$).

Conversely, by Lemma 6.29$(1)\Rightarrow (5)$, (resp.  by Lemma 6.6$(1)\Rightarrow (5)$), imply that h admits a stem function if h is rotationally equivariant, resp. rotationally invariant. $\square$

Proposition 6.31

Let $h:{{\mathbb {H}}}\rightarrow {\mathbb {R}}$ be a slice function with $\Delta 'h=0$.

Then there exists a slice-preserving regular function f such that $h=\mathfrak {R}\, (f)$.

Proof

Since h is real valued and a slice function, it is also rotationally equivariant and rotationally invariant (due to Lemma 6.30). Being rotationally equivariant implies $\Delta 'h=\Delta _*h$. Being rotationally invariant implies

$$\begin{aligned} h(x+yI)=h(x-yI) \,\, \forall x,y\in {{\mathbb {R}}},\ \forall I\in {\mathbb {S}}\end{aligned}$$

which in turn implies that

$$\begin{aligned} \partial _I h \end{aligned}$$

vanishes on the real line. It follows that $(\partial _*f)(x)=\frac{1}{2} (\partial _1 f)(x)\in {{\mathbb {R}}}$ for all $x\in {{\mathbb {R}}}$. Hence all the assumptions of Theorem 6.22 (2) are fulfilled, and we may deduce that $h=g+k$ where g is regular, k is anti-regular, and both g and k are slice preserving. The condition $h(q)\in {{\mathbb {R}}}$ is equivalent to $h(q)-\overline{h(q)}=0$. Therefore

$$\begin{aligned} g(q)-\overline{k(q)}=\overline{g(q)}-k(q)\,\, \forall q\in {{\mathbb {H}}}. \end{aligned}$$

The left-hand side of this equation is a regular function, while the right-hand side is anti-regular. Thus both must be constant. That the right-hand side is constant, implies:

$$\begin{aligned} k(q)= \overline{g(q)}-\overline{g(0)}+k(0)\,\, \forall q\in {{\mathbb {H}}}. \end{aligned}$$

Hence

$$\begin{aligned} h(q)=g(q)+k( q)=g(q)+\overline{g(q)}-\overline{g(0)}+k(0) =2 \mathfrak {R}\left( g(q)\right) -\overline{g(0)}+k(0) \ \ \forall q\in {{\mathbb {H}}}. \end{aligned}$$

Finally, $h({{\mathbb {H}}})\subset {{\mathbb {R}}}$ implies $-\overline{g(0)}+k(0)\in {{\mathbb {R}}}$. This proves the assertion for

$$\begin{aligned} f(q)=2 g(q)-\overline{g(0)}+k(0). \end{aligned}$$

$\square$

Proposition 6.32

Let u be real valued and rotationally invariant (in the sense of Definition 6.4) $C^2$-function. Let f be regular.

Then

$$\begin{aligned} \Delta '(u\circ f)=\int _{{\mathbb {S}}} \left( (\Delta _* u)\circ (R_wf)\right) |(\partial _*f)(S_wq)|^2 \mathrm{{d}}\mu (w)\quad \end{aligned}$$

Proof

Note that a real-valued rotationally invariant function $u:{{\mathbb {H}}}\rightarrow {{\mathbb {R}}}$ is automatically a slice function. (Lemma 6.30) Hence $\Delta 'u$ is well defined.

The claim of the proposition is a consequence of the complex computation

$\Delta (u \circ f)= \left( (\Delta u)\circ f\right) |(\partial _*f)(z)|^2$ (applied on ${{\mathbb {C}}}_I$) and of the definition of $\Delta '$. For more details, see the proof of the next proposition. $\square$

Proposition 6.33

Let $u :{{\mathbb {H}}}\rightarrow {\mathbb {R}}$ be a rotationally invariant $C^2$-function with $\Delta 'u=0$. Let $f :{{\mathbb {H}}}\rightarrow {{\mathbb {H}}}$ be a slice-preserving regular function, then $u \circ f$ is such that $\Delta ' (u\circ f)=0.$

Proof

First observe that u is a slice function, because it is real valued and rotationally invariant (Lemma 6.30). Next we prove that, under the hypotheses of the proposition,

$$\begin{aligned} R_w (u \circ f)= u \circ (R_w (f)) \,\,\, \forall \,\, w \in {\mathbb {S}}. \end{aligned}$$

(8)

Indeed $\forall \,\, w \in {\mathbb {S}}$:

$$\begin{aligned} R_w ( u\circ f)&= w(u(f(w^{-1}qw)))w^{-1} = w(u(R_w (f))w^{-1} \\&= S_w ^{-1} (u \circ R_w (f)) = u ( R_w (f)). \end{aligned}$$

Then, by definition, $\Delta ' (u \circ f) =\Delta _* \int \limits _{w \in {\mathbb {S}}} R_w (u \circ f) d \mu .$ By (8),

$$\begin{aligned}&\Delta _* \int \limits _{{\mathbb {S}}} R_w(u \circ f) d \mu (w)=\Delta _* \int \limits _{{\mathbb {S}}} u \circ R_w(f) d \mu (w)= \int \limits _{ {\mathbb {S}}} (\Delta _* (u \circ R_w f) d \mu (w) \\&\quad =\int \limits _{{\mathbb {S}}} {(\Delta _* u)\circ (R_w(f))}{|(R_w(f))'|^2} d \mu (w)\\&\quad =\int \limits _{{\mathbb {S}}} {(\Delta _* u)\circ (R_w(f))}{|(f)' (S_w(q))|^2} d \mu (w)=0 \end{aligned}$$

where $g' : =\partial _* g$. $\square$

Proposition 6.34

Let $u :{{\mathbb {H}}}\rightarrow {\mathbb {R}}$ be a $C^2$-function such that $\Delta ' u\equiv 0$ on ${{\mathbb {H}}}\setminus {{\mathbb {R}}}$. Then u admits no real isolated zero.

Remark 6.35

At a real point $\Delta 'u$ is defined only if u is a slice function. But in the proposition $\Delta 'u$ is only considered for points outside ${{\mathbb {R}}}$. Hence one does not need to require u to be a slice function.

Proof

Assume the contrary, i.e., assume that u has an isolated zero in a point $a\in {{\mathbb {R}}}$. Then there exists an open neighborhood W of a such that u has no zero on $W\setminus \{a\}$. For dimension reasons, $W\setminus \{a\}$ is connected. Thus u is either everywhere positive or everywhere negative on $W\setminus \{a\}$. Without loss of generality, assume that $u>0$ on $W\setminus \{a\}$.

Define

$$\begin{aligned} {\tilde{u}}(q)=\int _{\mathbb {S}}(R_wu)(q) \mathrm{{d}}\mu (w). \end{aligned}$$

For q sufficiently close to a (but $q\ne a$) we have ${\mathbb {S}}_q\subset W\setminus \{a\}$. For such q we have

$$\begin{aligned} (R_wu)(q)>0\ \forall w\in {\mathbb {S}}\end{aligned}$$

and therefore ${\tilde{u}}(q)>0$. On the other hand, $\tilde{u}(a)=u(a)=0$, because $a\in {{\mathbb {R}}}$. Thus ${\tilde{u}}$ has a strict local minimum in a.

By construction $\Delta 'u=\Delta _*{\tilde{u}}$ on ${{\mathbb {H}}}\setminus {{\mathbb {R}}}$. Fix $I\in {\mathbb {S}}$. By definition, on ${{\mathbb {C}}}_I$ the operator $\Delta _*$ agrees with the ordinary complex Laplacian, if we identify ${{\mathbb {C}}}_I\simeq {{\mathbb {C}}}$ as usual. Thus ${\tilde{u}}$ restricts to a $C^2$-function on ${{\mathbb {C}}}_I$ which is harmonic on ${{\mathbb {C}}}_I\setminus {{\mathbb {R}}}$. By continuity of $\Delta {\tilde{u}}$, the function ${\tilde{u}}$ is harmonic on the whole of ${{\mathbb {C}}}_I$. Thus we obtain a harmonic function on ${{\mathbb {C}}}_I\simeq {{\mathbb {C}}}$ with a strict local minimum in a. This is impossible. $\square$

7 A Kind of Poisson Formula

7.1 ${{\mathbb {H}}}$-Valued Measures

Theorem 7.1

Let $p\in {{\mathbb {H}}}$ and let $S\subset {{\mathbb {H}}}$ be a 3-dimensional sphere such that p is in its interior. Let $\Omega$ denote a circular domain containing both S and its interior.

Then there exists an ${{\mathbb {H}}}$-valued measure $\mu$ on S which is absolutely continuous with respect to the euclidean measure such that

$$\begin{aligned} f(p)=\int _{S} f(q)\mathrm{{d}}\mu (q) \end{aligned}$$

for every regular function f defined on $\Omega$.

Proof

We first discuss the special case where $p\in {\mathbb {R}}$. In this case for each $I\in {\mathbb {S}}$ the restriction of f to ${\mathbb {C}}_I$ is holomorphic, and ${\mathbb {C}}_I$ and S intersect in a 1-dimensional sphere which contains p in its interior. We thus may construct $\mathrm{{d}}\mu$ first taking the measure on $S\cap {\mathbb {C}}_I$ given by the classical Poisson formula, and then averaging over $I\in {\mathbb {S}}$ with respect to any probability measure of ${\mathbb {S}}.$

Now assume $p\not \in {\mathbb {R}}$. Fix $I\in {\mathbb {S}}$ such that $p\in {\mathbb {C}}_I$. Let $c=s+vJ$ ($s,v\in {\mathbb {R}}, v>0, J\in {\mathbb {S}}$) denote the center of the sphere S and $\rho$ its radius. Define ${{\bar{G}}}=\{t+yi\in {\mathbb {C}}: t,y\in {\mathbb {R}}, y\ge 0, \exists \,\, H\in {\mathbb {S}}: t+yH\in S\}$.

Then

$$\begin{aligned} {{\bar{G}}} = \{ (t+yi): \exists \,\, H\in {\mathbb {S}}: (t-s)^2 + |yH-vJ|^2 = \rho ^2 \}. \end{aligned}$$

We observe that ${\mathbb {S}}$ is connected and that $H\mapsto |yH-vJ|^2$ (for fixed $y,v>0,J\in {\mathbb {S}}$) defines a continuous map which evidently takes its maximum in $H=-J$ (with $(y+v)^2$ as its value) and its minimum in $H=J$ (with value $|y-v|^2$).

From this we may deduce :

$$\begin{aligned} {{\bar{G}}} = \{ (t+yi): |t-s|\le \rho ,\quad |y-v| \le \sqrt{ \rho ^2 -|t-s|^2} \le |y+v| \}. \end{aligned}$$

Let us now fix $t\in {\mathbb {R}}$ and investigate for which $y>0$ we have $t+iy\in {{\bar{G}}}$. We define $K=\sqrt{ \rho ^2 -|t-s|^2}$ and obtain the following condition:

$$\begin{aligned}&|y-v| \le \sqrt{ \rho ^2 -|t-s|^2}=K \le |y+v|\\&\quad \iff |y-v| \le K \le |y+v|\\&\quad \iff v-K\le y \le v+K \text { and }-v+K\le y\\&\quad \iff |v-K| \le y \le v+K. \end{aligned}$$

It follows that the interior G of ${{\bar{G}}}$ is simply connected and therefore biholomorphic to the unit disc.

Let ${\tilde{p}}=x+yi\in {{\mathbb {C}}}$ such that $x,y\in {{\mathbb {R}}}$, $y\ge 0$ and $p=x+yH$ for some $H\in {\mathbb {S}}$. Then ${\tilde{p}}$ is in the interior of G.

We fix such a biholomorphic map $\psi :G\rightarrow \Delta$ and recall that it extends continuously to the respective boundaries. We may and do require $\psi ({\tilde{p}})=0$.

By the classical mean value theorem

$$\begin{aligned} F(0)=\int _0^1\int _0^{2\pi } F(re^{i\theta }) \frac{\mathrm{{d}}\theta }{2\pi } d\sigma \end{aligned}$$

for every holomorphic function $F:{\mathbb {C}}\rightarrow {\mathbb {C}}$, every $r>0$ and every probability measure $\sigma$ on [0, 1].

Pulling-back with $\psi$ yields a probability measure $d\xi$ on G such that

$$\begin{aligned} F(p)=\int _G F(w)d\xi (w) \end{aligned}$$

(9)

for every holomorphic function F. The measure $d\xi$ constructed in this way is absolutely continuous, if the measure $\sigma$ on [0, 1] used in the construction is taken to be absolutely continuous.

For each point $t+yi\in G$ we have a 2-sphere $t+y{\mathbb {S}}$ in ${{\mathbb {H}}}$. Let V denote the “imaginary subspace” of ${{\mathbb {H}}}$, i.e., the ${{\mathbb {R}}}-$vector subspace of ${{\mathbb {H}}}$ generated by $y{\mathbb {S}}$. The intersection of the 3-sphere S with real affine subspace $t+V$ is a sphere (of dimension $\le 2$). Thus $S\cap (t+y{\mathbb {S}})$ is an intersection of two spheres in a three-dimensional real affine space and therefore again a sphere.

We let $\eta$ denote the involution defined by sending each element of $\Sigma _{t,y}=S\cap (t+y{\mathbb {S}})$ to its antipodal element.

Since $\Sigma _{t,y}\subset (t+y{\mathbb {S}})$, for every $q\in \Sigma _{t,y}$ there are $J,H\in {\mathbb {S}}$ such that $q=t+yJ$ and $\eta (q)=t+yH$.

By the generalized representation formula (Proposition 5.3) we have

$$\begin{aligned} f(t+yI)= M_1(J,H) f(q) + M_2(J,H) f(\eta (q)) \quad \forall q\in \Sigma _{t,y} \end{aligned}$$

for every regular function f.

With $m_1(q):=M_1(J,H)$ and $m_2(q)=M_2(J,H)$ we obtain continuous functions $m_i:\Sigma _{t,y} \rightarrow {{\mathbb {H}}},$ for $i=1,2,$ such that

$$\begin{aligned} f(t+yI)= m_1(q) f(q) + m_2(q) f(\eta (q)) \quad \forall q\in \Sigma _{t,y} \end{aligned}$$

for every regular function f.

In particular

$$\begin{aligned} f(t+yI)= \int _{q\in \Sigma _{t,y}} m_1(q) f(q) + m_2(q) f(\eta (q)) \mathrm{{d}}\alpha (q) \end{aligned}$$

for every probability measure $\alpha$ on $\Sigma _{t,y}$. Hence we may choose an absolutely continuous probability measure $\beta _{t,y}$ on $\Sigma _{t,y}$ such that

$$\begin{aligned} f(t+yI)= \int _{\Sigma _{t,y}} f(q) d\beta (q)\quad \forall f \end{aligned}$$

(10)

We recall that regular functions restrict to holomorphic ones on ${\mathbb {C}}_I$.

We may therefore combine the above constructions (see equations (9),(10)) to obtain

$$\begin{aligned} f(p)=\int _{t+yi\in G} \int _{q\in \Sigma _{t,y}} f(q) \mathrm{{d}}\beta (q) d\xi (t+yi) \end{aligned}$$

(with $\Sigma _{t,y}=S\cap (t+y{\mathbb {S}})$). $\square$

7.2 Poisson’s Formula

Proposition 7.2

(Poisson’s formula) Let $\mu$ denote a probability measure on ${\mathbb {S}}$. Let $u :\overline{{\mathbb {B}}_R} \rightarrow {\mathbb {R}}$ be a rotationally invariant $C^2$- function. Assume that $\Delta 'u\equiv 0$.³ Let $a \in {\mathbb {R}}$. Then the following formula holds:

$$\begin{aligned} u(a)=\frac{1}{2\pi } \int \limits _{{\mathbb {S}}} \int \limits _{0}^{2\pi } \frac{R^2-a^2}{|R \cdot e^{I\theta }-a|^2}u(R \cdot e^{I\theta })\mathrm{{d}}\theta \mathrm{{d}}\mu (I) \end{aligned}$$

Proof

Due to Lemma 6.30 the function u is a slice function. Thus we may conclude from Proposition 6.31 that u is the real part of a slice-preserving regular function f. Therefore for each $I\in {\mathbb {S}}$, the restriction of u to ${{\mathbb {C}}}_I$ is the real part of a holomorphic function from ${{\mathbb {C}}}_I$ to ${{\mathbb {C}}}_I$ and the above formula follows from the complex Poisson formula. $\square$

Remark 7.3

As in Proposition 4.1, it is possible to generalize the above Poisson Formula at any $a \in {\mathbb {H}}$ with an integration on the circularization of $\partial \Delta (a,r) \cup \partial \Delta ({\overline{a}},r)$ instead of an integration on $\partial {\mathbb {B}}_R.$

8 A Jensen’s Formula

The goal of this section is to prove a quaternionic version of Jensen’s formula. For this purpose we need Blaschke factors.

8.1 Quaternionic $\rho$-Blaschke Factors

In this subsection we are going to reproduce some results proved in [2, 3] for a modification of quaternionic Blaschke factors.

Definition 8.1

Given $\rho >0$ and $a\in {{\mathbb {H}}}$ such that $|a|<\rho$. We define the $\rho$-Blaschke factor at a as the following semi-regular function on ${\mathbb {H}}$:

$$\begin{aligned} B_{a,\rho }:{{\mathbb {H}}}\rightarrow {\hat{{{\mathbb {H}}}}},\quad B_{a,\rho }(x):=(\rho ^{2}-x{{\bar{a}}})*(\rho (x-a))^{-*}. \end{aligned}$$

We observe that

$$\begin{aligned} B_{a,\rho }&= (\rho ^2-q{{\bar{a}}})*(q-{{\bar{a}}}) \left( \rho (q^2-q(a+{{\bar{a}}})+|a|^2)\right) ^{-*}\\&= (q^2(-{{\bar{a}}}) +q(\rho ^2+{{\bar{a}}} ^2) -\rho ^2\bar{a})\left( \rho (q^2-q(a+{{\bar{a}}})+|a|^2)\right) ^{-1} \end{aligned}$$

(using that $g(q)^{-*}=(g(q))^{-1}$ for any slice-preserving function g, hence in particular for $g(q)=\rho (q^2-q(a+\bar{a})+|a|^2)$).

In particular,

$$\begin{aligned} |B_{a,\rho }(0)|=\left| \frac{\rho }{a}\right| , \,\, \text {if} \,\, a \ne 0 \end{aligned}$$

and

$$\begin{aligned} |B_{a,\rho }^{-*}(0)|=\left| \frac{a}{\rho }\right| . \end{aligned}$$

Remark 8.2

We observe that $(B_{a,\rho })^{-*}$ has a zero of multiplicity one at a and no other zeros or poles in ${{\mathbb {B}}}_\rho$.

The following is a consequence of Theorem 5.5 of [2].

Theorem 8.3

Given $\rho >0$ and $a\in {{\mathbb {H}}}$. The $\rho$-Blaschke factors $B_{a,\rho }$ have the following properties:

• they satisfy $B_{a,\rho }({{\mathbb {H}}}\setminus {\mathbb {B}}_{\rho })\subset {{\mathbb {B}}}_1$ and $B_{a,\rho }({\mathbb {B}}_{\rho })\subset {{\mathbb {H}}}\setminus {{\mathbb {B}}}_1$.

• they send the boundary of the ball $\partial {\mathbb {B}}_{\rho }$ in the boundary of the ball $\partial {{\mathbb {B}}}_1$.

8.2 Jensen’s Formula

First we prove a variant of Jensen’s formula for the special case where there are neither zeros nor poles.

Proposition 8.4

Let $\rho >0$ and let f be a regular function defined in a neighbourhood of $\overline{{\mathbb {B}}_{\rho }}$. Assume that f has no zeros in $\overline{{\mathbb {B}}_{\rho }}$.

Let $\mu$ be a probability measure on ${\mathbb {S}}$.

Then

$$\begin{aligned} \log |f(0)| \le \displaystyle \frac{1}{2\pi }\displaystyle \int _0^{2\pi } \int _{{\mathbb {S}}}\log |f(\rho \cos \theta +\rho \sin \theta I)|\mathrm{{d}}\mu (I)\mathrm{{d}}\theta \end{aligned}$$

with equality if f is slice preserving.

Proof

Fix an imaginary unit I. Choose another imaginary unit J such that $IJ=-JI$ (i.e., I and J are supposed to be orthogonal). Thus, using the “Splitting Lemma” 2.6, there are two holomorphic functions g, h with values in ${{\mathbb {C}}}_I$ defined on a neighborhood of ${{\bar{\Delta }}}_\rho =\{z\in {{\mathbb {C}}}_I:|z|\le \rho \}$ such that

$$\begin{aligned} f(q)=g(q)+h(q)J,\ \ \forall q\in \Delta _\rho ={{\mathbb {B}}}_\rho \cap {{\mathbb {C}}}_I. \end{aligned}$$

Then $|f(q)|^2=|g(q)|^2+|h(q)|^2$. Now, $\log \left( |g|^2+|h|^2\right)$ is subharmonic for any two holomorphic functions $g,h:{{\mathbb {C}}}\rightarrow {{\mathbb {C}}}$. Thus we have subharmonicity of $\log |f|^2$ and consequently

$$\begin{aligned} \log |f(0)|\le \frac{1}{2\pi }\int _0^{2\pi } \log |f(\rho e^{It})|dt \end{aligned}$$

Finally, by integration over the sphere of imaginary units we obtain the assertion. $\square$

In order to deal with the general case (where the function f is allowed to have zeros or poles) we need some preparations.

Lemma 8.5

Let f, g be regular functions on an open neighborhood of $\partial {{\mathbb {B}}}_\rho =\{q\in {{\mathbb {H}}}:|q|=\rho \}$.

Assume that $|g(q)|=1$ for all $q\in \partial {{\mathbb {B}}}_\rho$.

Then $|f(q)|=|(f*g)(q)|$ and $|g^{-*}(q)|=1$ for all $q\in \partial {{\mathbb {B}}}_\rho$.

Proof

The formula

$$\begin{aligned} |p^{-1}qp|= |q|,\ \ \forall p\in {{\mathbb {H}}}^*,q\in {{\mathbb {H}}}\end{aligned}$$

implies that $f(q)^{-1}qf(q)\in \partial {{\mathbb {B}}}_\rho$ whenever $q\in \partial {{\mathbb {B}}}_\rho$. Combined with

$$\begin{aligned} (f*g)(q)=f(q)g\left( f(q)^{-1}qf(q) \right) \quad \hbox {for}\, q \,\hbox {with}\, f(q)\ne 0 \end{aligned}$$

and $|g(q)|=1\ \forall q\in \partial {{\mathbb {B}}}_\rho$ we obtain

$$\begin{aligned} |(f*g)(q)|=|f(q)|\ \ \forall q\in \partial {{\mathbb {B}}}_\rho . \end{aligned}$$

If we apply this equation to $f=g^{-*}$, we obtain

$$\begin{aligned} 1=|(g^{-*}*g)(q)|=|(g^{-*})(q)|\ \ \forall q\in \partial {{\mathbb {B}}}_\rho . \end{aligned}$$

$\square$

Proposition 8.6

Let f be a semi-regular function on a neighborhood of $\bar{{\mathbb {B}}}_\rho$, with neither zeros nor poles on $\partial {{\mathbb {B}}}_{\rho }$.

Then there exist “$\rho$-Blaschke factors” $B_1,\ldots ,B_r$ and a regular function without zeros $f_0$ such that:

$$\begin{aligned} f=f_0*B_1*\ldots *B_r. \end{aligned}$$

Here a function B is called $\rho$-Blaschke factor, if $B=B_{a,\rho }$ or $B=B_{a,\rho }^{-*}$ for an element $a\in {{\mathbb {B}}}_\rho$.

Proof

Let g, h be regular functions such that $f=g^{-*}*h$. First we claim that there exist $\rho$-Blaschke factors $B_1,\ldots , B_s$ and a regular function ${\tilde{h}}$ without zeros such that $f=g^{-*}*{\tilde{h}}*B_1*\ldots * B_s$ . We proceed recursively. If h admits a zero in a point $a\in {{\mathbb {B}}}_\rho$, then there exists an element $b\in {\mathbb {S}}_a$ such that $h=h_0*(q-b)$. Recall that

$$\begin{aligned} B_{b,\rho }=(\rho ^2-q{{\bar{b}}})*(\rho (q-b))^{-*} = (\rho (q-b))^{-*} *(\rho ^2-q{{\bar{b}}}) \end{aligned}$$

and therefore

$$\begin{aligned} (q-b)=\frac{1}{\rho }\left( \rho ^2-q{{\bar{b}}}\right) * B_{b,\rho }^{-*}. \end{aligned}$$

Thus $f=g^{-*}*h_1*B_{b,\rho }^{-*}$ with

$$\begin{aligned} h_1(q)=h_0(q)\frac{1}{\rho } * \left( \rho ^2-q{{\bar{b}}}\right) \end{aligned}$$

being regular. Repeating this procedure recursively, we obtain a regular function ${\tilde{h}}$ without zeros in ${{\bar{{{\mathbb {B}}}}}}_\rho$ and $\rho$-Blaschke factors $B_1,\ldots , B_s$ such that

$$\begin{aligned} f=g^{-*}*{\tilde{h}}*B_1*\ldots * B_s \end{aligned}$$

Define

$$\begin{aligned} f_1=g^c*({\tilde{h}}^{-*})^c \end{aligned}$$

Then $f_1$ is regular and

$$\begin{aligned} f=(f_1^{-*})^c*B_1*\ldots * B_s \end{aligned}$$

Repeating the above process, we obtain a regular function $\phi$ without zeros and $\rho$-Blaschke factors $B'_1,\ldots B'_t$ such that

$$\begin{aligned} f_1=\phi * (B'_1*\ldots * B'_t) \end{aligned}$$

Consequently

$$\begin{aligned} f&=\left( \left( \phi * (B'_1*\ldots * B'_t) \right) ^{-*}\right) ^c *B_1*\ldots * B_s \\&=(\phi ^{-*})^c * \left( ((B'_1)^{-*})^c\right) * \ldots (((B'_t)^{-*})^c) * \left( B_1*\ldots * B_s \right) \end{aligned}$$

$\square$

Proposition 8.7

(Jensen’s Formula) Let $\Omega =\Omega _D$ be a circular domain of ${{\mathbb {H}}}$ and let $f:\Omega \rightarrow {{\mathbb {H}}}\cup \{ \infty \}$ be a semi-regular function. Let $\rho >0$ such that the ball $\overline{{\mathbb {B}}_{\rho }}\subset \Omega$, $f(0)\ne 0,\infty$ and such that $f(y)\ne 0, \infty$, for any $y\in \partial {\mathbb {B}}_{\rho }$.

Assume that (for the function f)

• $\{r_{k}\}_{k=1,2,..}$ are the punctual zeros,

• $\{ w_n \}_{n=1,2,...}$ are the punctual real poles,

• $\{{\mathbb {S}}_{a_{i}}\}_{i=1,2,..}$ are the spherical zeros,

• $\{{\mathbb {S}}_{b_{j}}\}_{j=1,2,..}$ are the spherical poles,

everything repeated accordingly to their multiplicity. Let $\mu$ be a probability measure on ${\mathbb {S}}$.

Then:

$$\begin{aligned} \log |f(0)| \le&\displaystyle \frac{1}{2\pi }\displaystyle \int _0^{2\pi } \int _{{\mathbb {S}}}\log |f(\rho \cos \theta +\rho \sin \theta I)|\mathrm{{d}}\mu (I)\mathrm{{d}}\theta \, \\&-\displaystyle \sum _{|r_{k}|<\rho }\left( \log \displaystyle \frac{\rho }{|r_{k}|}\right) + \displaystyle \sum _{|w_{n}|<\rho }\left( \log \displaystyle \frac{\rho }{|w_{n}|}\right) \\&- 2\displaystyle \sum _{|a_{j}|<\rho }\left( \log \displaystyle \frac{\rho }{|a_{j}|}\right) + 2\displaystyle \sum _{|b_{j}|<\rho }\left( \log \displaystyle \frac{\rho }{|b_{j}|} \right) . \end{aligned}$$

Using the language of divisors as explained in Sect. 3 we may reformulate this as follows:

Proposition 8.8

(Jensen’s Formula) Let $\Omega =\Omega _D$ be a circular domain of ${{\mathbb {H}}}$ and let $f:\Omega \rightarrow {{\mathbb {H}}}\cup \{ \infty \}$ be a semi-regular function. Let $\rho >0$ such that the ball $\overline{{\mathbb {B}}_{\rho }}\subset \Omega$, $f(0)\ne 0,\infty$ and such that $f(y)\ne 0, \infty$, for any $y\in \partial {\mathbb {B}}_{\rho }$. Let $\mu$ be a probability measure on ${\mathbb {S}}$.

Then:

$$\begin{aligned} \log |f(0)|\le & {} \displaystyle \frac{1}{2\pi }\displaystyle \int _0^{2\pi } \int _{{\mathbb {S}}}\log |f(\rho \cos \theta +\rho \sin \theta I)|\mathrm{{d}}\mu (I)\mathrm{{d}}\theta \, +\nonumber \\&\displaystyle -\sum _{|p_k|<\rho } m_k\log \frac{\rho }{|p_k|} \end{aligned}$$

(11)

for $div(f)=\sum m_k\{p_k\}$.

Proof

If f has neither zeros, nor poles, this is Proposition 8.4.

For the general case, we consider $div(f)=\sum _k m_k\{p_k\}$. First of all, since $\overline{{\mathbb {B}}_{\rho }}\subset \Omega$, it follows from Corollary 2.14 that there are only finitely many k with $m_k\ne 0$, hence the sums in the statement are finite and $\sum _k |m_k|<\infty$.

From Proposition 8.6 we deduce that f may be represented in the form

$$\begin{aligned} f=f_0*B_1*\ldots *B_r \end{aligned}$$

where $f_0$ is regular on a neighborhood of ${{\bar{{{\mathbb {B}}}}}}_\rho$ with neither zeros nor poles and each $B_i$ equals $B_{p_i,\rho }^{\epsilon _i *}$ for some $p_i\in {{\mathbb {B}}}_\rho$ and $\epsilon _i\in \{+1,-1\}$.

Now

$$\begin{aligned} \log |f(0)|=\log |f_0(0)| +\sum _i \log |B_i(0)|= \log |f_0(0)| -\sum _i \epsilon _i\log \frac{\rho }{|p_i|} \end{aligned}$$

On the other hand

$$\begin{aligned} |f(q)|=|f_0(q)| \ \ \forall q\in \partial {{\mathbb {B}}}_\rho \end{aligned}$$

because $|B_i(q)|=1$ for all $i\in \{1,\ldots ,r\}$ and all $q\in \partial {{\mathbb {B}}}_\rho$.

Furthermore,

$$\begin{aligned} \log |f_0(0)| \le \displaystyle \frac{1}{2\pi }\displaystyle \int _0^{2\pi } \int _{{\mathbb {S}}}\log |f_0(\rho \cos \theta +\rho \sin \theta I)|\mathrm{{d}}\mu (I)\mathrm{{d}}\theta \end{aligned}$$

(with equality if f is slice preserving) due to Proposition 8.4.

Combining these facts, we obtain the assertion. $\square$

Remark 8.9

For every semi-regular function f,  its symmetrization $f^s=N(f)=f*f^c$ is slice preserving. Therefore:

$$\begin{aligned} \log |f^s(0)|= & {} \displaystyle \frac{1}{2\pi }\displaystyle \int _0^{2\pi } \int _{{\mathbb {S}}}\log |f^s(\rho \cos \theta +\rho \sin \theta I)|\mathrm{{d}}\mu (I)\mathrm{{d}}\theta \, + \nonumber \\&-2{\displaystyle \sum _{|p_k|<\rho } m_k\log \frac{\rho }{|p_k|} } \end{aligned}$$

(12)

for $div(f)=\sum m_k\{p_k\}$.

However, there is no similar formula for $Tr(f)=f+f^c$, because $div(f+f^c)$ is not completely determined by div(f), whereas $div(f^s)=2\cdot div(f)$.

Definition 8.10

Let f be a slice regular function on ${\mathbb {B}}_R.$ For all $0< r < R$ we define:

$$\begin{aligned} M_f (r)= & {} \sup \limits _{|q|=r} |f(q)| \,\,; \\ P_f (r)= & {} \text {number of punctual zeros of f with multiplicities} \,\, ; \\ S_f (r )= & {} \text {number of spherical zeros of f with multiplicities}; \end{aligned}$$

$$\begin{aligned} n_f(r)=P_f(r)+2S_f(r). \end{aligned}$$

Then

$$\begin{aligned} n_f(r)=\sum _{|a_k|\le r} m_k \end{aligned}$$

for a regular function f with divisor $div(f)=\sum m_k\{a_k\}$.

Corollary 8.11

Let f be a slice regular function defined in a neighborhood of $\overline{{\mathbb {B}}_R}$ and such that $f(0) \ne 0.$ Then

$$\begin{aligned} n_f(r)=P_f(r)+2S_f(r) \le \frac{\log M_{f} (R) -\log |f(0)| }{\log R - \log r} \end{aligned}$$

(13)

for any $0<r <R.$

Proof

First we observe that

$$\begin{aligned} \log M_f(R)\ge \displaystyle \frac{1}{2\pi }\displaystyle \int _0^{2\pi } \int _{{\mathbb {S}}}\log |f(R\cos \theta +R\sin \theta I)|\mathrm{{d}}\mu (I)\mathrm{{d}}\theta . \end{aligned}$$

Therefore the Jensen’s inequality (11) implies:

$$\begin{aligned} \log M_f(R) - \log |f(0)|&\ge \sum _{|p_k|<R} m_k\log \frac{R}{|p_k|}\\&= \left( \sum _{|p_k|<R} m_k\log R \right) - \sum _{|p_k|<R} m_k\log |p_k|\\&= n_f(R)\log R - \sum _{|p_k|<R} m_k\log |p_k|\\&= n_f(R)\log R - \sum _{|p_k|\le r} m_k\log |p_k| -\sum _{r<|p_k|<R} m_k\log |p_k|\\&\ge n_f(R)\log R - \sum _{|p_k|\le r} m_k\log r -\sum _{r<|p_k|<R} m_k\log R\\&= n_f(R)\log R - n_f(r)\log r -(n_f(R)-n_f(r))\log R\\&= n_f(r)\left( \log R - \log r \right) .\\ \end{aligned}$$

Thus

$$\begin{aligned} \log M_f(R) - \log |f(0)| \ge n_f(r)\left( \log R - \log r \right) \end{aligned}$$

(14)

for all $0<r<R$ such that f has no zeros on $\partial {{\mathbb {B}}}_R$. By continuity (in R) it follows that (14) holds without any assumption whether there are zeros on $\partial {{\mathbb {B}}}_R$ or not.

This yields the assertion. $\square$

Corollary 8.12

Let $f:{{\mathbb {B}}}_1\rightarrow {{\mathbb {B}}}_1$ be a regular function with $f(0)\ne 0$.

Then there is no zero of f in ${{\mathbb {B}}}_r$ for any $r<|f(0)|$.

Proof

Assume the contrary. Then $n_f(r)\ge 1$ while

$$\begin{aligned} \lim _{R\rightarrow 1} \frac{\log M_{f} (R) -\log |f(0)| }{\log R - \log r} \le \frac{-\log |f(0)|}{-\log r}<1 \end{aligned}$$

leading to a contradiction. $\square$

The interested reader can find in [4] and in [30] other results about Jensen’s Formula but in a slightly different context.