Effects of Thermocapillary and Natural Convection During the Melting of PCMs with a Liquid Bridge Geometry

Abstract

The results of a numerical investigation of the melting of a PCM occupying an axisymmetric volume in the presence of gravity are presented. The PCM is held between two circular supports maintained at different temperatures. The melting process, which is analyzed for n-octadecane, is affected by a combination of thermocapillary and natural convection. If the PCM is heated from above, the convective motion driven by the thermocapillary force is opposed by the buoyant force, which reduces the heat transfer rate. If the PCM is heated from below, natural convection acts in the same sense as thermocapillary convection and the heat transfer rate is increased. The volume $\mathcal {V}$ of the PCM relative to an ideal cylinder, which selects the shape of the PCM/air interface, is found to play an important role. The overall effect of natural convection on heat transfer is characterized by the ratio of the melting time in microgravity to that of the same system with gravity. This gain factor is greater (less) than unity when heating from below (above) and depends strongly on $\mathcal {V}$, particularly for smaller PCM volumes.

Introduction

Phase change materials (PCMs) have found numerous and wide-ranging applications where they are used to improve efficiency and control temperatures. Their proper function depends not only on their capacity to absorb, store, and release large quantities of energy but also on the efficiency with which this energy can be transferred between the PCM and the system it is integrated into. Among the many available materials — both natural and synthetic — organic PCMs like alkanes and fatty acids are popular choices because of their stability, convenient melting temperatures and non-reactive chemistry. One of the potential problems with organic PCMs, however, is their relatively low thermal conductivity, which slows the heat transfer process and limits their effective use to comparably slow thermal cycles.

A number of researchers have investigated ways to enhance the performance of organic PCMs by increasing their heat transfer rates with strategies relying, for example, on the addition of more conductive materials such as metal fins, meshes, and tubes (Ettouney et al. 2004; Agyenim et al. 2009; Fernandes et al. 2012; Atal et al. 2016; Cabeza et al. 2002). Active strategies can also be implemented, such as the use of a heat exchanger with a circulating fluid in contact with the PCM (Medrano et al. 2009; Koželj et al. 2020). While these types of strategies are suitable for many applications, there are other situations — in the space industry, for example — where the addition of heavy materials or active mechanisms may be problematic (Salgado Sanchez et al. 2020b).

An attractive alternative strategy for enhancing heat transport, in a simple and passive way, is to make use of the temperature gradient that is naturally present to encourage convection. Convective flow can be significantly more efficient for heat transport than thermal diffusion (conduction) and, therefore, can greatly increase the responsiveness of the PCM device. In the presence of gravity, for instance, buoyancy leads to natural convection, which, depending on the geometry of the device and the relative orientation of the temperature gradient and gravitational acceleration, will affect the heat transfer rate to various extent (Gau and Viskanta 1986; Roy and Sengupta 1990; Wang et al. 1999; Khodadadi and Zhang 2001; Shokouhmand and Kamkari 2013; Dhaidan and Khodadadi 2015). A second way in which thermal gradients can drive convection is via the thermocapillary effect, which has recently been studied as an alternative to natural convection in low-gravity environments (Madruga and Mendoza 2017b; Ezquerro et al. 2019; Ezquerro et al. 2020; Salgado Sanchez et al. 2020a, c).

The use of thermal Marangoni convection to enhance heat transfer requires a free surface (a potential drawback) yet many PCM designs already incorporate an air (gas) layer in order to mitigate the stress caused by expansion — a result of the volume difference between liquid and solid states. Thermocapillary convection will naturally occur in such devices and can be very effective at transferring heat (Salgado Sanchez et al. 2020a; Varas et al. 2021; Martínez et al. 2021; Borshchak Kachalov et al. 2022; Garcia-Acosta et al. 2022). It has the advantage that it does not depend on gravity and always has a positive effect on heat transport, independent of orientation. This is in contrast to natural convection, which is ineffective when heat must be transferred downward against the buoyant force (i.e., in the case of heating from above).

The presence of two distinct sources of convection in PCM devices that include a free surface offers the possibility of generating more vigorous motion and, thus, more efficient heat transfer (Madruga and Mendoza 2017a; Borshchak Kachalov et al. 2021). The interaction of these two mechanisms is complex, however, and is not well-understood. It depends on numerous parameters aside from the relative orientation of gravity and the thermal gradient.

Here, we focus on the melting process in n-octadecane, which is a common organic PCM. The PCM is assumed to take a quasi-cylindrical form corresponding to the equilibrium shape of a liquid bridge with its axis parallel to gravity. This shape is not cylindrical, since gravity pulls the liquid downward, and is characterized by a narrowed upper section and a distended lower section. It is axisymmetric, however, and we assume that the flow maintains this symmetry, which allows a two-dimensional model to be used and permits a much larger selection of parameters to be studied.

The parametric study conducted here looks at the effect of gravity (Bond number), aspect ratio, temperature difference (Marangoni, Rayleigh and Stefan numbers) and PCM volume on the melting process. Aside from the expected and important difference between heating from above and heating from below, there is an interesting dependence of the melting process on volume (domain shape), including the possibility that larger volumes of PCM may sometimes melt faster than smaller ones. Compared to the closely-related work of Varas et al. (2021), where the analogous melting process is analyzed in microgravity, the focus here is on the effect that gravity has on the heat transfer rate rather than on pattern selection. We note that, in microgravity, the appearance of oscillatory thermocapillary flow during melting has a weaker effect on the melting time than it does here, especially when gravity acts to reinforce the thermocapillary force when heating from below.

The work presented here begins with a description of the mathematical formulation in "Mathematical Formulation" section, followed by results for selected parameters when heating from above or below in "Melting Dynamics When Heating from Above" and "Melting Dynamics When Heating from Below" sections, respectively. "Heat Transport" section summarizes the effect on heat transport of the key parameters mentioned above, focusing on a comparison with the microgravity case (i.e., when there is no natural convection) analyzed by Varas et al. (2021). Conclusions are drawn in "Conclusions".

Mathematical Formulation

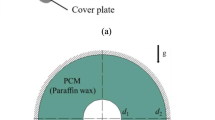
We consider a volume V of PCM in a liquid bridge configuration with longitude L and radius R in reduced gravity. One of the circular supports is held at a cold temperature $T_C = T_M$, equal to the melting temperature, while the other is heated to a temperature $T_H > T_M$ in order to drive the phase change. A sketch of the problem (in the case of heating from above) is shown in Fig. 1.

Fig. 1

Sketch of the problem considered: a PCM in liquid bridge configuration with variable radius $r = \xi (z)$ caused by the (reduced) gravity

As a simple and more computationally feasible starting point, only axisymmetric dynamics are considered as in the previous work of Varas et al. (2021), which precludes a description of azimuthal modes and other three-dimensional flows (Seta et al. 2021, 2022); such three-dimensional effects may be important in some cases and will be analyzed elsewhere. Surface deformation is taken into account but not dynamically (Kamotani et al. 2003; Kawamura and Ueno 2006; Kawamura et al. 2012; Shevtsova et al. 2013). This assumption of a fixed surface profile is consistent with the small deformation associated with thermocapillary convection (Montanero et al. 2008). Similarly, small changes in the surface profile do not qualitatively modify the behaviour of the thermocapillary flow. The largest error comes from the fact that assuming constant volume is inconsistent with the density difference between solid and liquid states (Huang and Zhou 2020; Vu 2023). Despite this, recent work found good agreement between experiments and simulations in related PCM systems (Salgado Sanchez et al. 2020c) while small volume changes, like those associated with the PCM expansion during melting, were shown to have minimal effect on heat transport in analogous liquid bridge configurations (Varas et al. 2021); this is also consistent with the results discussed in "Heat Transport" section.

The phase change occurs while the PCM is surrounded by air, which means that there is a liquid/gas interface created during the melting process. This evolving interface has a nonuniform temperature gradient that drives thermocapillary convection in the liquid phase and this mechanism can contribute significantly to the transport of heat from the hot support to the solid PCM and/or the cold support. The transfer of heat from the liquid to the air across the interface, which increases the complexity and computational cost of the model [see, e.g., Martínez et al. (2021)], is not considered here.

Governing Equations

The behaviour of the fluid is assumed to be laminar and incompressible and is described by the Navier-Stokes equations (Landau and Lifshitz 1987):

$$\begin{aligned} \nabla \cdot {\textbf {u}} = 0, \end{aligned}$$

(1)

$$\begin{aligned} \rho \dfrac{\partial {{\textbf {u}}}}{\partial { t}}+\rho \left( {\textbf {u}}\cdot \nabla \right) \;{\textbf {u}} = -\nabla p + {\nabla (\mu \nabla {\textbf {u}})}+\rho \,{\textbf {g}}, \end{aligned}$$

(2)

where ${\textbf {u}} = (u, \, w)$ is the two-dimensional (axisymmetric) velocity field (radial component u and axial component w), p is the pressure field, $\mu$ is the dynamic viscosity, $\rho$ is the density, and ${\textbf {g}} = -\textrm{g} \,\textbf{e}_z$ is the gravitational acceleration directed along the axis of symmetry.

The energy equation includes the contributions of sensible heat, associated with temperature changes, and latent heat, associated with the phase change (Voller et al. 1987; Egolf and Manz 1994):

$$\begin{aligned} \begin{aligned} \rho c_p\left( \dfrac{\partial T}{\partial t}+{\textbf {u}}\cdot \nabla T\right) ={\nabla (k \nabla T)}- \rho c_L\left( \dfrac{\partial f}{\partial t}+{\textbf {u}}\cdot \nabla f\right) . \end{aligned} \end{aligned}$$

(3)

Here, T is the temperature field, $c_p$ is the specific heat capacity at constant pressure, k is the thermal conductivity, $c_L$ is the specific latent heat, and f is the liquid fraction defined by

$$\begin{aligned} f(T) = \left\{ \begin{array}{lll} 0 & \widetilde{T} <-\delta _T/2,\\ \frac{1}{2}+\frac{\widetilde{T}}{\delta _T}+\frac{1}{2\pi } \sin \left( {\frac{2 \pi \widetilde{T}}{\delta _T}}\right) &{} |\widetilde{T}|\le \delta _T /2, \\ 1 &{} \widetilde{T} > \delta _T /2, \end{array} \right. \end{aligned}$$

(4)

where $\widetilde{T}\equiv T- T_M$.

This liquid fraction depends on the temperature T and changes continuously from 0 to 1, which correspond, respectively, to pure solid and pure liquid PCM. The parameter $\delta _T$ characterizes an interval of temperatures called the “mushy region” where solid and liquid phases can coexist (Egolf and Manz 1994). For n-octadecane, its value is estimated to lie between 1 K and 4 K, depending on various parameters of the system (Ho and Gaoe 2009; Velez et al. 2015). Here, we use $\delta _T$ = 1 K for consistency with related work (Salgado Sanchez et al. 2020a, 2021; Garcia-Acosta et al. 2022).

The system is treated continuously, with properties that depend on the local temperature and have appropriate limits for the solid and liquid phases (denoted by subscripts S and L, respectively). This dependence is written in terms of the liquid fraction f(T) defined above:

$$\begin{aligned} \rho (T) = \rho _S + ( \rho _L-\rho _S)\,f(T), \end{aligned}$$

(5a)

$$\begin{aligned} \mu (T) = \mu _S + (\mu _L-\mu _S)\,f(T), \end{aligned}$$

(5b)

$$\begin{aligned} c_p(T) = c_{pS} + (c_{pL}-c_{pS})\,f(T), \end{aligned}$$

(5c)

$$\begin{aligned} k(T) = k_S + (k_L - k_S)\,f(T), \end{aligned}$$

(5d)

where $\mu _S$ is a virtual viscosity for the solid, which is taken to be several orders of magnitude greater than that of the liquid (Voller et al. 1987). The numerical value $\mu _S = 10^3$ Pa s is chosen based on convergence tests in Salgado Sanchez et al. (2020a).

The liquid density is assumed to vary linearly with temperature (Landau and Lifshitz 1987) as

$$\begin{aligned} \rho _L = \rho _0\left[ 1-\beta (T-T_M)\right] , \end{aligned}$$

(6)

where $\rho _0$ is the density at $T=T_M$ and $\beta$ is the thermal expansion coefficient.

Boundary Conditions

At the free surface $r = \xi (z)$ (see Fig. 1), there is a balance between pressure, viscous stress and surface tension $\sigma$ (Gligor et al. 2022a, b) expressed by

$$\begin{aligned} -\textbf{n}\cdot \left[ -p\,{\textbf {I}}+\mu \left( \nabla \textbf{u}+\left( \nabla \textbf{u}\right) ^T\right) \right] = \sigma (\nabla _s\cdot \textbf{n})\,\textbf{n}-\nabla _s\,\sigma , \end{aligned}$$

(7)

where ${\textbf {I}}$ is the identity matrix, $\textbf{n} = \nabla \xi /|\nabla \xi |$ is a unit vector perpendicular to the free surface, and $\nabla _s = (\textbf{I}-\textbf{n}\,\textbf{n}^T)\nabla$ is the surface gradient operator. The thermocapillary effect is described via the linearized dependence of surface tension $\sigma$ on T:

$$\begin{aligned} \sigma = \sigma _0 - \gamma \left( T-T_M\right) , \end{aligned}$$

(8)

where the thermocapillary coefficient $\gamma =| \partial \sigma / \partial T|$ is evaluated at the reference temperature $T_M$. We neglect heat transfer across the thermocapillary interface and impose the adiabatic boundary condition

$$\begin{aligned} \nabla T \cdot \textbf{n} = 0, \end{aligned}$$

(9)

which is a simple and more computationally feasible starting point for the analysis of PCM melting. It should be noted, however, that the exchange of heat with the surrounding air can be relevant to both overall heat transport and pattern selection during the melting process (Martínez et al. 2021) and this depends crucially on the ambient temperature (Melnikov and Shevtsova 2014). In fact, techniques for controlling pattern selection in a liquid bridge through the manipulation of its thermal environment are under investigation (Shevtsova et al. 2013; Stojanovic and Kuhlmann 2020; Gaponenko et al. 2020).

At the circular supports, the contact line is assumed to be pinned with

$$\begin{aligned} \xi = R \;\;\;\; \textrm{at} \;\;\;\; z = \mp L/2, \end{aligned}$$

(10)

while no-slip conditions are imposed for $\textbf{u}$:

$$\begin{aligned} {\textbf {u}} = 0 \;\;\;\;\textrm{at} \;\;\;\; z = \mp L/2 \;\;\;\; \forall \, r, \end{aligned}$$

(11)

and fixed temperatures for T:

$$\begin{aligned} T = T_C \;\;\;\;\textrm{at} \;\;\;\; z = \mp L/2 \;\;\;\; \forall \, r,\end{aligned}$$

(12a)

$$\begin{aligned} T = T_H \;\;\;\;\textrm{at} \;\;\;\; z = \pm L/2 \;\;\;\; \forall \, r, \end{aligned}$$

(12b)

where the signs in Eqs. (12a) and (12b) correspond, respectively, to heating from above or below.

Finally, the assumption of axisymmetry implies no dependence on $\theta$ and

$$\begin{aligned} u = 0, \quad \dfrac{\partial w}{\partial r} = 0, \quad \dfrac{\partial T}{\partial r} = 0 \;\; \textrm{at} \;\; r = 0 \;\;\;\; \forall z, \end{aligned}$$

(13a)

after which the volume conservation condition simplifies to

$$\begin{aligned} \int \pi \, \xi (z)^2 \, \textrm{d} z = V. \end{aligned}$$

(14)

Governing Parameters

It is convenient to define dimensionless variables for spatial coordinates, time and temperature:

$$\begin{aligned} \widehat{r} = \frac{r}{L}, \;\; \widehat{z} = \frac{z}{L}, \;\; \tau = t \left( \frac{\alpha }{L^2}\right) , \;\; \Theta = \frac{T-T_M}{T_H-T_M}, \end{aligned}$$

where $\alpha = k_L/(\rho _0 c_{pL})$ is the thermal diffusivity of the liquid. The physical properties are nondimensionalized with respect to those of the liquid:

$$\begin{aligned} \widehat{\rho } = \frac{\rho }{\rho _0}, \;\; \widehat{\mu } = \frac{\mu }{\mu _L}, \;\; \widehat{c_p} = \frac{c_p}{c_{pL}}, \;\; \widehat{k} = \frac{k}{k_L}. \end{aligned}$$

(15)

The dynamics of the system depend on the ratio of these properties between solid and liquid phases,

$$\begin{aligned} \widetilde{\rho } = \frac{\rho _S}{\rho _0}, \;\; \widetilde{\mu } = \frac{\mu _S}{\mu _L}, \;\; \widetilde{k} = \frac{k_S}{k_L}, \;\; \widetilde{c_p} = \frac{c_{pS}}{c_{pL}}, \end{aligned}$$

(16)

and on the Prandtl number

$$\begin{aligned} \textrm{Pr}=\frac{\mu _L}{\rho _0\alpha }, \end{aligned}$$

(17)

the Marangoni, Rayleigh and Stefan numbers

$$\begin{aligned} \textrm{Ma} = \frac{\gamma L\left( T_H-T_M\right) }{\mu _L\alpha }, \end{aligned}$$

(18)

$$\begin{aligned} \textrm{Ra} = \frac{\textrm{g} \rho _0 \beta L^3\left( T_H-T_M\right) }{\mu _L \alpha }, \end{aligned}$$

(19)

$$\begin{aligned} \textrm{Ste} = \frac{c_{pL}\left( T_H-T_M\right) }{c_L}, \end{aligned}$$

(20)

which characterize the relative importance of thermocapillary convection, buoyancy and latent heat, respectively, the Bond number

$$\begin{aligned} \textrm{Bo} = \frac{\rho _0 \textrm{g} R^2}{\sigma _0}, \end{aligned}$$

(21)

the Capillary number

$$\begin{aligned} \textrm{Ca} = \frac{\gamma (T_H-T_M)}{\sigma _0}, \end{aligned}$$

(22)

the dimensionless volume

$$\begin{aligned} \mathcal {V} = \frac{V}{\pi R^2 L}, \end{aligned}$$

(23)

which compares the PCM volume with that of a perfect cylinder with the same length L and radius R, and the aspect ratio

$$\begin{aligned} \Gamma = \frac{L}{R}, \end{aligned}$$

(24)

which characterizes the slenderness of the liquid bridge.

Using the values for n-octadecane from Table 1, one obtains

$$\begin{aligned} \widetilde{\rho } = 1.11, \quad \widetilde{k} = 2.42, \quad \widetilde{c_p} = 0.88, \quad \textrm{Pr} = 52.53. \end{aligned}$$

(25)

The values of the other dimensionless parameters are varied by changing the applied temperature difference $\Delta T = T_H - T_M$, the gravity level $\textrm{g}$, and the liquid bridge geometry via the selection of R and the PCM volume V. Note that the length of the bridge is fixed at $L = 22.5$ mm, as in the microgravity experiments proposed by the ‘Effect of Marangoni Convection on Heat Transfer in Phase Change Materials’ project (Laverón 2021; Porter et al. 2023).

Table 1 Physical properties of n-octadecane, reproduced from Salgado Sanchez et al. (2020c)

Numerical Approach

The deformation of the surface caused by thermocapillary flows in liquid bridges was studied experimentally (Montanero et al. 2008) and numerically (Shevtsova et al. 2008) and found to be proportional to the Capillary number. For the present simulations, Ca takes small values with $\textrm{Ca} < 0.12$, which justifies neglecting this dynamic deformation and taking the shape of the liquid bridge to be static and independent of the melting dynamics and its associated flow.

The numerical resolution of the melting process is thus undertaken in two steps. First, the shape of the liquid bridge is obtained by solving the static stress balance condition at the free surface. That domain is then fixed and used to simulate the melting process with a combination of thermocapillary and natural convection. This approach is analogous to that used in Varas et al. (2021) and consistent with previous research on melting in geometries determined by surface tension. Khodadadi and Zhang (2001), for example, simulated the effect of thermocapillary flows on melting droplets after assuming a fixed spherical domain.

Computing PCM Shape

The free surface is assumed to be that defined by a volume V of PCM when completely melted (i.e., a liquid bridge configuration). The interface location $r = \xi (z)$ (see Fig. 1) is determined by calculating the static equilibrium between surface tension and the local pressure at the interface described by Eq. (7), which takes the form (Slobozhanin and Perales 1993)

$$\begin{aligned} \sigma \nabla \cdot \textbf{n} + P - \rho \textrm{g} z= 0, \end{aligned}$$

(26)

where the term proportional to $\nabla _s \, \sigma$ has been neglected since $\textrm{Ca} \ll 1$. Note that $P - \rho \textrm{g} z$ is the static pressure distribution and P refers to the pressure value at $z = r = 0$, which enforces the conservation of volume described by Eq. (14). The solution must also respect the pinning condition $\xi (\pm L/2) = R$.

Equation (26) is solved using an in-house code based on second-order finite differences (Varas et al. 2021) to obtain the interface shape $\xi (z)$; the solutions were validated against the results of Laveron-Simavilla and Checa (1997) and Laveron-Simavilla and Perales (1995).

Computing PCM Melting

The governing equations described in "Governing Equations" section are applied within the domain defined by $\xi (z)$ and the two supports, and resolved using the finite element method with the commercial software COMSOL Multiphysics.

With this approach, the stress balance at the PCM/air interface simplifies to

$$\begin{aligned} \mu \nabla _n\,{\textbf {u}}_t = -\gamma \nabla _t T, \end{aligned}$$

(27)

where subscripts n and t refer to normal and tangential components, respectively, and is applied together with slip and adiabatic boundary conditions:

$$\begin{aligned} {\textbf {u}}\cdot {\textbf {n}} = 0, \quad \nabla T \cdot {\textbf {n}} = 0. \end{aligned}$$

(28)

The pressure field is computed after imposing $p = P$ at $z = r = 0$, derived from Eq. (26).

The initial condition for the temperature field is $T_0 = 25$ °C, where n-octadecane is a solid. The velocity field is, therefore, initialized with ${\textbf {u}}=0$. Temporal evolution is begun with the backward Euler method and continued using a backward differentiation formula (BDF).

The numerical scheme, including the selection of mesh size and other numerical parameters, builds on the work of Salgado Sanchez et al. (2020c), where two-dimensional simulations were validated against experiments. The time step, which is between 0.00005 s and 0.25 s, depends on Ma, the mesh, and $\Gamma$, and is selected in light of the Courant–Friedrichs–Lewy (CFL) convergence criterion. Additionally, streamline and crosswind stabilization techniques are used to avoid numerical instabilities (Salgado Sanchez et al. 2020a). The same numerical approach was also recently used in Varas et al. (2021) to simulate the melting of PCMs in axisymmetric melting bridges in microgravity.

Organization of Results

The numerical results presented below are obtained for particular choices of Ma and $\Gamma$ and, in each case, over a range of $\mathcal {V}$. The parameters are selected in order to analyze the melting dynamics in both steady and oscillatory flow regimes, and to include both small and moderate aspect ratio geometries, respectively. We follow Varas et al. (2021) and use $\textrm{Ma} = 15519, 155186$ and $\Gamma = 2, 4$. Recall that both geometries have $L = 22.5$ mm.

For the selected values of $\Gamma$, the dimensionless volume is varied within the limits of stability of the melted PCM, which is a liquid bridge. For $\Gamma = 2$ this corresponds to $\mathcal {V} \in [0.45, \, 2.51]$ and, for $\Gamma = 4$, to $\mathcal {V} \in [0.56, \, 4.26]$ (Slobozhanin and Perales 1993).

The gravity level is measured using the Bond number, which compares gravity to surface tension; see Eq. (21). The results below are obtained for $\Gamma = 2$ and $\textrm{Bo} = 2$, which corresponds to $\textrm{g} = 0.558$ m/s$^2$, and for $\Gamma = 4$ and $\textrm{Bo} = 0.2$, which corresponds to $\textrm{g} = 0.223$ m/s$^2$. We consider both heating from above and heating from below.

Note that varying gravity changes the Rayleigh number, which also depends on the applied temperature difference; see Eq. (19). The relative importance of buoyant and thermocapillary flows can be quantified independently of $\Delta T$ by the dynamic Bond number

$$\begin{aligned} \text {Bo}_\textrm{dyn} = \frac{\textrm{Ra}}{\textrm{Ma}} = \frac{\rho _0 \textrm{g} \beta L^2}{\gamma }, \end{aligned}$$

(29)

which takes the values of 2.37 and 0.95 for $\textrm{Bo} = 2$ and 0.2, respectively.

As in the works of Salgado Sanchez et al. (2020a) and Varas et al. (2021), the melting process is described in terms of the rate of increase of the liquid fraction $\mathcal {L}$, measured as a percentage of the PCM volume.

Melting Dynamics When Heating from Above

Steady Flow Regime

We begin with a study of the case when the PCM is heated from above with the moderate value of $\textrm{Ma} = 15519$, where there is no oscillatory flow in microgravity (Varas et al. 2021). For each choice of Bo and $\Gamma$, the dimensionless volume $\mathcal {V}$ is varied between 0.8 and 1.5.

Figure 2 shows the evolution of the streamlines and temperature field during melting for $\Gamma = 2$, $\textrm{Bo}=2$, and two selected volumes: (a) $\mathcal {V} = 0.8$ and (b) $\mathcal {V} = 1.1$. For both volumes, the behaviour is qualitatively similar as the solid/liquid front descends past the narrower region near the upper support and into the more distended region near the lower support.

Fig. 2

Snapshots (at labelled times) showing the evolution of the solid/liquid front, streamlines and temperature field. Heat is applied from above with $\Gamma = 2$, $\textrm{Bo}=2$, $\text {Bo}_\textrm{dyn}=2.37$, $\textrm{Ma} = 15519$, and (a) $\mathcal {V} = 0.8$, (b) $\mathcal {V} = 1.1$

While the initial phase of melting is controlled by conduction, convection quickly emerges as the dominant process in the dynamics of the system. This convection results both from the thermocapillary effect, which was studied in isolation in Varas et al. (2021), and from buoyancy. In the case of heating from above, these two sources of convection act in an opposing manner. Thermocapillary flow draws warmer liquid away form the heated support toward the solid/liquid front, which increases the melting rate. Natural convection, on the other hand, acts to maintain the warmer (less dense) fluid at the top, near the heated support, which is expected to reduce the overall convective flow and, thus, the melting rate.

The melting process generally proceeds in a similar manner to that observed in microgravity (Varas et al. 2021) but with a noncylindrical free surface shape determined by the balance between gravity and surface tension. The solid/liquid front begins parallel to the heated support but rapidly develops curvature near the surface as that region melts faster due to thermocapillary convection. At a certain moment (near $\tau = 3.362$ for $\mathcal {V} = 0.8$ and $\tau = 2.936$ for $\mathcal {V} = 1.1$) this part of the front reaches the cold support. Subsequently, it can only move inward toward the axis ($r = 0$) of the bridge. The PCM is completely melted by $\tau = 5.035$ (29500 s) in both cases.

One notable difference compared to the microgravity case considered by Varas et al. (2021) is the appearance of a vortex near the solid/liquid front and, in the latter stages of melting, near the lower support; see Fig. 2. The absence of this vortex in weightlessness indicates that it is due to natural convection. The vortex associated with thermocapillary convection is larger and concentrated near the surface. In larger volumes, there can be a second such vortex above the widened portion of the bridge. Overall, however, the melting process with other (comparable) volumes of PCM is analogous to that described above, with minor changes in the shape of the interface and in the final melting time.

Figure 3 shows the rate of change of the liquid fraction during the melting process for the dimensionless volumes $\mathcal {V} = 0.8$ (red curve), $\mathcal {V} = 1$ (black), $\mathcal {V} = 1.1$ (light blue), and $\mathcal {V} = 1.5$ (dark blue). The behaviour is similar in all cases. Initially, the liquid fraction increases very rapidly from zero (reflected in the divergent derivative) due to the large local thermal gradient and the associated diffusion of heat. The melting rate then decreases, reaches a minimum and increases again, with a relatively sharp local maximum occurring somewhat past the midpoint of the melting process. This is followed by another decrease and a second, broader, local maximum of lower amplitude just prior to the conclusion of melting. This second maximum is associated with a large vortex centred in the lower portion of the bridge.

Fig. 3

Rate of change of the liquid fraction versus time for $\Gamma = 2$, $\textrm{Bo}=2$, $\text {Bo}_\textrm{dyn}=2.37$, $\textrm{Ma} = 15519$ and dimensionless volumes $\mathcal {V} = 0.8$ (red curve), 1 (black), 1.1 (light blue) and 1.5 (dark blue). The temperature field and streamlines at selected moments can be seen in Fig. 2 for $\mathcal {V}$ = 0.8 and 1.1

The first local maximum in the melting rate occurs for a similar configuration of temperature and streamlines in all cases and corresponds to the solid/liquid front reaching the bottom support; see the third snapshots of Fig. 3. As this happens, the large vortex generated by the thermocapillary flow carries more warm liquid to the wider portion of the bridge, which produces the local maximum in heat transport.

Note that when the system is heated from above, as here, the narrow portion of the bridge melts first and the principal vortex of the thermocapillary flow does not move substantially into the wider part of the bridge for a considerable time. The latter stage of melting is associated with a second vortex near the cold support that is due to natural convection and leads to an increase in the melting rate. The importance of this effect means that, unlike in microgravity, a larger volume of PCM does not necessarily require a longer melting time (compare, for example, the $\mathcal {V} = 0.8$ and $\mathcal {V} = 1$ cases of Fig. 3).

Fig. 4

Snapshots (at labelled times) showing the evolution of the solid/liquid front, streamlines and temperature field. Heat is applied from above with $\Gamma$ = 4, $\textrm{Bo}=0.2$, $\text {Bo}_\textrm{dyn}=0.95$, $\textrm{Ma} = 15519$ and $\mathcal {V} = 1$

Fig. 5

Rate of change of the liquid fraction versus time for $\Gamma$ = 4, $\textrm{Bo}=0.2$, $\text {Bo}_\textrm{dyn}=0.95$, $\textrm{Ma} = 15519$ and dimensionless volumes $\mathcal {V} = 0.8$ (red curve), 1 (black) and 1.5 (blue). The temperature field and streamlines at selected moments can be seen in Fig. 4 for $\mathcal {V} = 1$

Figure 4 shows the advance of the melting front and the associated streamlines and temperature field for the same parameters as above, except for the reduced gravity level of $\textrm{Bo} = 0.2$ and the larger aspect ratio of $\Gamma = 4$. The dimensionless volume $\mathcal {V}$ is unity. For this case, melting finishes by $\tau = 2.816$ (16500 s). The dynamics of this system are broadly similar to those of the previous case with $\textrm{Bo} = 2$ and $\Gamma = 2$. One difference, aside from the smaller (dimensional) melting time, is the appearance of a secondary vortex near the hot support that does not disappear with time. The effect of this vortex is increased homogenization of the temperature field.

Fig. 6

Snapshots (at labeled times) showing the evolution of the solid/liquid front, streamlines and temperature field. Heat is applied from above with $\Gamma = 2$, $\text {Bo} = 2$, $\text {Bo}_\textrm{dyn}=2.37$, $\text {Ma} = 155186$ and (a) $\mathcal {V} = 0.9$ or (b) $\mathcal {V} = 1.2$

Figure 5 shows the rate of change of the liquid fraction over time for the dimensionless volumes $\mathcal {V} = 0.8$ (red curve), $\mathcal {V} = 1$ (black) and $\mathcal {V} = 1.5$ (blue). For the two lower volumes, there is a local maximum shortly after melting begins. This relatively small feature corresponds to the movement of the solid/liquid front past the narrow (neck) of the bridge. A more pronounced maximum in the melting rate occurs later (near $\tau = 2$ for $\mathcal {V} = 0.8, 1$) as the solid/liquid front reaches the cold support. After this, melting advances inward and a vortex forms from the effect of natural convection. This produces another increase in melting rate that accelerates until the end of the phase change. Overall, the dynamics are similar for different volumes.

Oscillatory Flow Regime

Figure 6 illustrates melting for the case of $\Gamma = 2$ and $\textrm{Bo} = 2$ but with a larger applied temperature corresponding to $\textrm{Ma} = 155186$. The oscillations that appear with this increased level of thermocapillary forcing are analogous to those reported in Salgado Sanchez et al. (2021) and Varas et al. (2021). Here we consider the two dimensionless volumes $\mathcal {V} = 0.9$ (upper row in Fig. 6) and $\mathcal {V} = 1.2$ (lower row).

As before, the initial stage of melting is dominated by conduction, but this is quickly followed by the emergence of thermocapillary convection near the surface, which rapidly melts a layer of PCM. Since the effective aspect ratio of this relatively thin liquid layer is larger at this value of Ma than in Fig. 4, there are more vortices (Salgado Sanchez et al. 2021,  2022). As melting progresses, the depth of the liquid layer near the surface increases, reducing its effective aspect ratio and the number of vortices it contains. At a certain point, the solid/liquid front reaches the cold support and subsequent melting proceeds inward. The final configuration after all material is melted is characterized by two main vortices located near the surface, one in the smaller narrow portion of the bridge and another in the wider portion. Their relative size depends on the volume and, in the case of $\mathcal {V} = 0.9$, there is a third, smaller vortex associated with natural convection located toward the interior of the cold support; it is absent in the microgravity case (Varas et al. 2021).

When oscillations appear, the vortices wander back and forth, growing or losing intensity in a periodic manner. The number of vortices can also vary during the oscillation, with some vortices splitting into smaller ones that merge again later (Varas et al. 2021; Salgado Sanchez et al. 2021).

The PCM with $\mathcal {V} = 0.9$ melts completely by $\tau = 0.768$ (4500 s) while that with $\mathcal {V} = 1.2$ takes until $\tau =0.870$ (5100 s). It can also be observed that the temperature field is generally more homogeneous in the distended portion of the bridge than in the narrower part.

Figure 7 shows the melting rate for dimensionless volumes $\mathcal {V} = 0.8$ (red), 1 (black), 1.2 (light blue) and 1.5 (dark blue). The corresponding curves are qualitatively similar. As melting begins, there is a rapid decrease from the initially divergent rate. Not long after this descent, the melting rate grows slightly again and reaches a local maximum that corresponds, as in previous cases, with the arrival of the solid/liquid front to the cold support. The melting rate then decreases once again but, in some cases, exhibits another local maximum before melting finishes. This phenomenon was also observed in microgravity and is related to the presence of a final narrow remnant of solid PCM in the center that melts relatively rapidly (Varas et al. 2021). Not all melting PCM systems experience this final maxima.

Fig. 7

Rate of change of the liquid fraction versus time for $\Gamma = 2$, $\text {Bo} = 2$, $\text {Bo}_\textrm{dyn}=2.37$, $\text {Ma} = 155186$ and dimensionless volumes $\mathcal {V} = 0.8$ (red curve), 1 (black), 1.2 (light blue) and 1.5 (dark blue). The temperature field and streamlines at selected moments can be seen in Fig. 6 for $\mathcal {V} = 1.2$

Figure 8 shows the evolution of the temperature field and streamlines during the melting process for $\Gamma = 4$, $\text {Bo} = 0.2$, and $\text {Ma} = 155186$ and the two dimensionless volumes $\mathcal {V} = 1$ (a) and $\mathcal {V} = 1.5$ (b). The phase change proceeds in much the same manner as the previous case with $\Gamma = 2$ and $\text {Bo} = 2$. The main differences, aside from geometry and melting time, are the number of vortices and the homogeneity of the temperature field. Here, the final configuration in the case of $\mathcal {V} = 1$ involves three vortices concentrated near the free surface, one in the upper narrow portion and two in the lower distended portion. There is no vortex due to natural convection near the cold support; compare with Fig. 6(a). If the volume is increased to $\mathcal {V} = 1.5$, the final configuration exhibits only two vortices. The oscillatory instability is again evident from the periodic back-and-forth motion of the vortex centers and changes in their intensity. Cycles of vortex splitting and fusion may also be seen.

Fig. 8

Snapshots (at labeled times) showing the evolution of the solid/liquid front, streamlines and temperature field. Heat is applied from above with $\Gamma = 4$, $\text {Bo} = 0.2$, $\text {Bo}_\textrm{dyn}=0.95$, $\text {Ma} = 155186$ and (a) $\mathcal {V} = 1$, (b) $\mathcal {V} = 1.5$

The difference in the temperature field is consistent with the lower level of gravity ($\text {Bo} = 0.2$ compared to $\text {Bo} = 2$) and the increased importance of thermocapillary flow with the thinner volume of PCM ($\Gamma = 4$ compared to $\Gamma = 2$); this increase in thermocapillary character is also reflected in the decrease of $\mathrm{Bo_\textrm{dyn}}$ from 2.37 to 0.95. Natural convection is, thus, less relevant, and warmer fluid can move downward more freely, which is evident in the temperature field near the surface.

The PCM bridge with $\mathcal {V} = 1$ melts by $\tau = 0.282$ (1650 s) while that with $\mathcal {V} = 1.5$ melts by $\tau = 0.299$ (1750 s). As in previous cases, it is not always true that larger volumes melt faster (here, the case with 50% more volume only requires a 6% greater melting time).

The evolution of the melting rate, shown in Fig. 9, is similar to that of previous cases. There is a local maximum when the solid/liquid front reaches the cold support and, in some cases, a smaller maximum near the end due to the rapid melting of a final thin solid zone in the interior of the bridge. This zone may even split into two, with an island of solid along the axis and another attached to the cold support.

Fig. 9

Rate of change of the liquid fraction versus time for $\Gamma = 4$, $\text {Bo} = 0.2$, $\text {Bo}_\textrm{dyn}=0.95$, $\text {Ma} = 155186$ and dimensionless volumes $\mathcal {V} = 0.8$ (red), 1 (black) and 1.5 (blue). The temperature field and streamlines at selected moments can be seen in Fig. 8 for $\mathcal {V} = 1$ and 1.5

The selection of the flow in the liquid phase and its primary features (number of vortices, oscillation frequencies, etc.) observed during the melting process can be associated with the behaviour observed in pure liquid bridges (Seta et al. 2021, 2022) by characterizing the liquid phase geometry with an effective aspect ratio and Marangoni number (Salgado Sanchez et al. 2022). The main features are also similar to those observed for buoyant-thermocapillary convection in thin liquid films (Shevtsova et al. 2003; Lappa 2017; Kudo and Ochi 2020).

Melting Dynamics When Heating from Below

Steady Flow Regime

The behaviour of a PCM bridge that is heated from below is notably different from that described above. The case with $\text {Ma} = 15519$, where oscillations do not occur, is illustrated in Fig. 10 through a series of snapshots showing the solid/liquid front, streamlines and temperature field for $\Gamma = 2$, $\text {Bo} = 2$ and $\mathcal {V} = 1$. In contrast to "Melting Dynamics When Heating from Above" section, melting begins from the distended portion of the bridge. The initial dominance of conductive heat transport is rapidly overshadowed by convection, which is driven both by the thermocapillary effect and by buoyancy. As before, the solid/liquid front advances faster along the surface than in the interior until it reaches the cold support. Subsequent melting proceeds inward until the solid is gone, which occurs by $\tau = 3.413$ (20000 s). Note that the initial phase of melting involves two vortices in the lower heated region while only one of those persists in the final flow, centered near the heated support and the surface; there is no small vortex near the cold support as there was in Fig. 2.

Fig. 10

Snapshots (at labeled times) showing the evolution of the solid/liquid front, streamlines and temperature field. Heat is applied from below with $\Gamma = 2$, $\text {Bo} = 2$, $\text {Bo}_\textrm{dyn}=2.37$, $\text {Ma} = 15519$ and $\mathcal {V} = 1$

The temperature field in Fig. 10 clearly shows the enhanced transport of heat in this orientation, a result of natural convection acting in concert with the thermocapillary flow. It is also significant that melting begins in the wider portion of the PCM bridge and that the large vortex seen there appears early and contributes to heat transport over nearly the entire melting process.

Fig. 11

Rate of change of the liquid fraction versus time for $\Gamma = 2$, $\text {Bo} = 2$, $\text {Bo}_\textrm{dyn}=2.37$, $\text {Ma} = 15519$ and dimensionless volumes $\mathcal {V}$ = 0.8 (red curve), 1 (black) and 1.5 (blue). The temperature field and streamlines at selected moments can be seen in Fig. 10

The melting rate can be seen in Fig. 11 for dimensionless volumes $\mathcal {V} = 0.8$ (red), 1 (black) and 1.5 (blue). The corresponding curves are qualitatively similar and characterized by two principal maxima. As in previous cases, the first of these coincides with the arrival of the solid/liquid front at the cold support; see the third snapshot in Fig. 10. The second maxima occurs at the end of the melting process and is associated with the formation of a final, narrow region of solid PCM along the axis of the bridge, which melts rapidly; see the penultimate snapshot in Fig. 10.

Fig. 12

Snapshots (at labeled times) showing the evolution of the solid/liquid front, streamlines and temperature field during melting. Heat is applied from below with $\Gamma = 4$, $\textrm{Bo} = 0.2$, $\text {Bo}_\textrm{dyn}=0.95$, $\textrm{Ma} = 15519$ and (a) $\mathcal {V} = 0.8$, (b) $\mathcal {V} = 1.05$

Fig. 13

Rate of change of the liquid fraction versus time for $\Gamma = 4$, $\textrm{Bo} = 0.2$, $\text {Bo}_\textrm{dyn}=0.95$, $\textrm{Ma} = 15519$ and dimensionless volumes $\mathcal {V} = 0.8$ (red curve), 1 (black), 1.05 (light blue), and 1.5 (dark blue). The temperature field and streamlines at selected moments can be seen in Fig. 12

A comparison with the same system heated from above shows that the small broad local maxima that occurs near the end in that case (see Fig. 3) is gone, yet a similar broad maxima appears prior to the first principal maxima. This shift is due to the reversed order of melting of the narrow and distended portions of the bridge in the two cases.

The evolution of the temperature field and streamlines with $\Gamma = 4$, $\textrm{Bo} = 0.2$ and the same Marangoni number of $\textrm{Ma} = 15519$ is shown in Fig. 12 with PCM volumes $\mathcal {V} = 0.8$ (a) and $\mathcal {V} = 1.05$ (b). There are few significant differences with the previous case apart from the geometry and the characteristic times. Due to the effect of gravitational convection, the temperature field is again warmer near the surface and the wider part of the bridge in comparison to the case of heating from above, but somewhat less so that in the previous case with stronger gravity ($\textrm{Bo} = 2$). During the first part of the melting process there are two vortices visible while only one of those, concentrated near the lower right, remains at the end. There is no additional vortex associated with the presence of natural convection (as in Fig. 6, for instance). The principal effect of gravity, as in the previous configuration, is to help move warm fluid to the solid/liquid front and, thus, to reduce the melting time. This reduction is furthered by the fact that melting begins in the larger distended portion of the bridge.

The melting rate is shown in Fig. 13 for dimensionless volumes $\mathcal {V} = 0.8$ (red), 1 (black), 1.05 (light blue), and 1.5 (dark blue). The curves are essentially the same as before, with minor differences. After decreasing from an initially large value, the melting rate increases again before reaching one or more local maxima. The principal maxima, which appears in all cases, corresponds to the arrival of the solid/liquid front at the cold boundary. An earlier, broader maxima may appear as the front moves past the narrow neck of the bridge (see the red curve for $\mathcal {V} = 0.8$). For $\mathcal {V} = 1.5$, there is a final increase prior to the completion of melting. This can again be explained by the terminal arrangement of the solid PCM, which can melt rapidly if a thin region is left at the end. A similar phenomenon can occur in microgravity (Varas et al. 2021).

Oscillatory Flow Regime

If the temperature of the hot boundary is increased until $\textrm{Ma} = 155186$, then oscillations appear that affect heat transport as well as the flow. Figure 14 shows a series of snapshots with $\Gamma = 2$, $\textrm{Bo} = 2$ and dimensionless volumes $\mathcal {V} = 0.8$ (a) and $\mathcal {V} = 1.2$ (b). The general evolution of the melting process is quite similar to the cases already described. Here, due to the more rapid melting along the surface compared to the case of $\textrm{Ma} = 15519$, the effective aspect ratio of the liquid layer during the early period of melting is higher and associated with a greater number of vortices Salgado Sanchez et al. (2021, 2022).

Fig. 14

Snapshots (at labeled times) showing the evolution of the solid/liquid front, streamlines and temperature field during melting. Heat is applied from below with $\Gamma = 2$, $\textrm{Bo} = 2$, $\text {Bo}_\textrm{dyn}=2.37$, $\textrm{Ma} = 155186$ and (a) $\mathcal {V} = 0.8$, (b) $\mathcal {V} = 1.2$

Near the end of the melting process for $\mathcal {V} = 0.8$, the solid PCM splits into two pieces as it rapidly melts; see the snapshot at $\tau = 0.219$. This separated PCM solution is permitted by the (fixed geometry) simulation but is unrealistic in the presence of gravity. Regardless of this, the final (fully melted) configuration is characterized in both cases by a large vortex with its center near the hot boundary and occupying the lower, wider portion of the bridge. A much smaller secondary vortex can be seen in the upper, narrow portion of the bridge near the cold boundary.

While there is no additional vortex associated with natural convection in this case either, the temperature of the fluid is notably higher than in Fig. 12, a result of stronger gravity, which helps drive the convection that carries warmer fluid toward the solid/liquid front (or the cold support). When heating from below, the large principal vortex appears early and contributes over a long period to heat transport. When oscillations appear, they are associated with displacement of the vortices and variation in their intensity. Vortices may also divide and merge again during the cycle.

Fig. 15

Rate of change of the liquid fraction versus time for $\Gamma = 2$, $\textrm{Bo} = 2$, $\text {Bo}_\textrm{dyn}=2.37$, $\textrm{Ma} = 155186$ and dimensionless volumes $\mathcal {V} = 0.8$ (red curve), 1 (black), 1.2 (light blue), and 1.5 (dark blue). The temperature field and streamlines at selected moments can be seen in Fig. 14

The melting rate, shown in Fig. 15, has similar features as before. The first local maximum occurs when the solid/liquid front reaches the cold boundary while, in some configurations such as $\mathcal {V} = 0.8$, there is a second maximum due to the formation of a thin region of solid PCM at the end of the process, which then melts rapidly.

Fig. 16

Snapshots (at labeled times) showing the evolution of the solid/liquid front, streamlines and temperature field during melting. Heat is applied from below with $\Gamma = 4$, $\textrm{Bo} = 0.2$, $\text {Bo}_\textrm{dyn}=0.95$, $\textrm{Ma} = 155186$ and $\mathcal {V} = 0.9$

The final configuration considered is with the same Marangoni number, $\textrm{Ma} = 155186$, but with $\Gamma = 4$ and $\textrm{Bo} = 0.2$. The melting process in this case is illustrated in Fig. 16 for dimensionless volume $\mathcal {V} = 0.9$. The large number of vortices that appear during the initial stage gradually reduces, leaving three at the end of the melting process (one more than with $\Gamma = 2$ and $\textrm{Bo} = 2$ in Fig. 14). This final solution is oscillatory, with both the vortex centers and their intensity changing periodically in time; merging and splitting may occur as well. Once again, the temperature of the fluid along the surface is elevated in comparison to the case of heating from above (although somewhat less than with $\Gamma = 2$ and the greater Bond number $\textrm{Bo} = 2$).

Fig. 17

Rate of change of the liquid fraction versus time for $\Gamma = 4$, $\textrm{Bo} = 0.2$, $\text {Bo}_\textrm{dyn}=0.95$, $\textrm{Ma} = 155186$ and dimensionless volumes $\mathcal {V} = 0.8$ (red curve), 0.9 (orange), 1 (black), and 1.5 (blue). The temperature field and streamlines at selected moments can be seen in Fig. 16

One notable feature is the formation of a thin region of solid PCM along the central axis (visible in the fourth snapshot at $\tau = 0.12$). Within a few seconds, this thin region melts, leaving a more triangular solid region that melts more gradually. Melting ends by $\tau$ = 0.234 (1370 s).

The behaviour of the melting rate over time, shown in Fig. 17 is qualitatively similar to previous cases, with the first local maximum occurring as the solid/liquid front reaches the cold boundary. Here, there is also a second local maximum corresponding to the rapid melting of the thin solid region; see the snapshot at $\tau = 0.12$ in Fig. 16.

Heat Transport

In this section, we investigate the overall effect on heat transport of the melting dynamics described above. The efficiency of heat transport in the presence of gravity is characterized by the gain factor $\mathcal {G}$, defined as the ratio between the melting time in microgravity [the $\textrm{Bo} = 0$ case is reproduced from Varas et al. (2021)] and that measured for the finite Bond numbers used here. This factor is greater than unity when natural convection contributes to the heat transport caused by thermocapillary convection and less than unity when it hinders it.

The gain factor is shown in Fig. 18 as a function of dimensionless volume. The upper panel (a) shows the results of simulations made with $\Gamma = 2$ and $\textrm{Bo} = 2$ while the lower panel (b) contains results for $\Gamma = 4$ and $\textrm{Bo} = 0.2$. In each case, there are four curves corresponding to $\textrm{Ma} = 15519$ (blue) and $\textrm{Ma} = 155186$ (red) with heating from above (inverted triangles) and from below (upright triangles).

Fig. 18

Summary of heat transfer efficiency (gain $\mathcal {G}$) versus dimensionless volume $\mathcal {V}$ for the selected values of $\textrm{Ma} = 15519$ (blue) and $\textrm{Ma} = 155186$ (red) and (a) $\Gamma = 2$, $\textrm{Bo} = 2$, $\text {Bo}_\textrm{dyn}=2.37$, (b) $\Gamma = 4$, $\textrm{Bo} = 0.2$, $\text {Bo}_\textrm{dyn}=0.95$. The horizontal line shows the microgravity case $\mathcal {G} = 1$. Configurations with heating from below (above) are shown with upright (inverted) triangles. The gain is greater than unity only when gravity generates convection that supports the heat transport of the thermocapillary flow

For both choices of Bo and $\Gamma$, the two cases with heating from above show $\mathcal {G} < 1$. This is because gravity acts to maintain the warmer fluid near the hot boundary, which suppresses convection (with respect to $\textrm{Bo} = 0$). In the opposite case of heating from below, buoyancy causes the warmer fluid to rise, which contributes to heat transfer and leads to $\mathcal {G} > 1$. Another contributing factor when heating from below is the large vortex that forms in the distended portion of the bridge, which appears earlier and makes a more significant contribution to heat transfer (compared to the vortex than forms when heating from above).

Figure 18 also shows that the gain $\mathcal {G}$ in heat transfer when heating from below diminishes with increasing volume, approaching an asymptotic value near one. This is more noticeable with greater heating, $\textrm{Ma} = 155186$. On the other hand, the variation of $\mathcal {G}$ when heating from above is less dramatic with weaker dependence on both Ma and $\mathcal {V}$ (especially evident for $\mathcal {V} < 1$). The fact that the variation of gain with volume is more evident with smaller $\Gamma$ is consistent with the results in microgravity (Varas et al. 2021).

Conclusions

The results of a numerical investigation into the melting of a PCM occupying an axisymmetric volume (i.e., a liquid bridge when fully melted) in the presence of gravity were presented. The system is supported between two circular base plates that are held at different temperatures. The melting process is affected by a combination of thermocapillary and natural convection and depends on the temperature difference, gravity level, aspect ratio and volume, as well as the physical properties of n-octadecane. The orientation of gravity with respect to the Marangoni force is also crucial and this was examined by heating either from above or from below. The shape of the surface was not allowed to vary, and was assumed to be determined by the static balance between gravity (hydrostatic pressure) and surface tension. The bridge geometry is thus characterized by an upper narrower region and a lower distended region.

The difference between heating from above and from below is both dramatic and easy to understand. If the PCM is melted from above, the warmer fluid must move contrary to the buoyant force in order to transfer its heat to the solid/liquid front. This reduces the strength of the flow due to thermocapillary convection and, thus, the rate of heat transfer. The melting time is generally greater than it would be in microgravity for the same system. On the other hand, if the PCM is melted from below, natural convection acts in the same sense as thermocapillary convection and heat transfer is augmented. The melting time, in this case, is generally less than for the same system in microgravity.

Another important difference between heating from above and below is related to the noncylindrical geometry (a result of gravity). When the lower distended portion of the bridge is melted first, the large vortex that forms in this wider region exists for a longer period of time compared to the case when melting begins from above and is, therefore, more influential in the melting process.

The dimensionless volume $\mathcal {V}$ is important in the melting process since it affects the shape of the surface as well as setting the volume of PCM that must be melted. In some cases, near the end of the melting process, a narrow region of solid PCM forms. This may split into separate solid regions (or not) and is associated with a local maximum in the melting rate. While not all configurations exhibit this effect, all cases considered do show an increase in the heat transfer rate that corresponds to the arrival of the solid/liquid front at the cold boundary, something that is also observed in microgravity (Varas et al. 2021).

An interesting fact for systems heated from above is that, unlike in microgravity, it is possible for a PCM of larger volume to melt faster than one of smaller volume. This is a result of the asymmetric shape of the bridge with gravity, which is narrower near the top and wider near the bottom, and may be associated with the appearance of a vortex driven by natural convection in the lower portion of the bridge.

The overall effect of gravity on heat transfer was characterized by the ratio of the melting time in microgravity to that of the same system with gravity. This gain factor, which is greater than unity for heating from below and less than unity for heating from above, shows a strong dependence on $\mathcal {V}$, particularly for smaller volumes where gravity is more influential for heat transfer. As $\mathcal {V}$ increases, the importance of gravity diminishes.

Finally, we draw attention to a couple of points that suggest themselves for future work. First, the axisymmetric dynamics considered here must be extended to three dimensions to capture rotating travelling waves, modes that are frequently observed in liquid bridges, and to analyze the effect of three-dimensional flows on heat transport, which is expected to be especially relevant for high Ma values. Second, future experiments are needed to evaluate the effect of heat exchange across the PCM/air interface and its influence on heat transport and pattern selection. Along with this, it may be of interest for those future PCM experiments to monitor the temperature of the adjacent air (gas) layer during the melting process or to incorporate some type of temperature control.