Convergence of numerical schemes for the solution of partial integro-differential equations used in heat transfer

Abstract

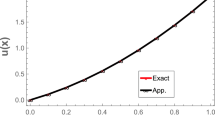
Integro-differential equations play an important role in may physical phenomena. For instance, it appears in fields like fluid dynamics, biological models and chemical kinetics. One of the most important physical applications is the heat transfer in heterogeneous materials, where physician are looking for efficient methods to solve their modeled equations. The difficulty of solving integro-differential equations analytically made mathematician to search about efficient methods to find an approximate solution. The present article is designed to supply numerical solution of a parabolic Volterra integro-differential equation under initial and boundary conditions. We have made an attempt to develop a numerical solution via the use of Sinc-Galerkin method, the convergence analysis via the use of fixed point theory has been discussed, and showed to be of exponential order. For comparison purposes, we approximate the solution of integro-differential equation using Adomian decomposition method. Sometimes, the Adomian decomposition method is a highly efficient technique used to approximate analytical solution of differential equations, applicability of Adomian decomposition method to partial integro-differential equations has not been studied in details previously in the literatures. In addition, we present numerical examples and comparisons to support the validity of these proposed methods.