1 Introduction

Low-permeability oil and gas reservoirs have become important exploratory and development fields in the world (Zou et al. 2017; Mu and Ji 2019). Horizontal well small-hole fracturing technology is an important production stimulation measure for low-permeability oil and gas reservoirs (Lei et al. 2018; Qu et al. 2019; Agarwal et al. 2019). In reservoirs, the expansion packer determines the outcomes of the fracturing technology. The expandable packer isolates the tubing and the borehole wall and then forms an annular space in Fig. 1. The annular space separates the oil and gas to achieve a layered fracture. As the core component of the expandable packer, the rubber affects fracturing during construction (Guo and Gao 2013). Currently, overlapped steel belts and steel cord rubber cylinders are used in rubber, but the residual deformation is large. When the pipe string is lifted up, the steel belt and steel cord are more likely to become stuck in the casing leading to underground accidents (Patel et al. 2019a, b). Nylon cord rubber has the advantages of small residual deformation and is easy to lift and lower the tubing string in low-permeability oil and gas reservoirs (Zhong et al. 2015; Akhtar et al. 2018; Pradie et al. 2008). However, it is associated with low-pressure-bearing and poor sealing performance. It is, therefore, important to analyze and optimize the structural parameters of the nylon cord rubber in expandable packer to meet the on-site requirements of high-pressure and fine fracturing in low-permeability oil and gas reservoirs (Li et al. 2017; Tian et al. 2019).

Fig. 1
figure 1

The schematic diagram of fracturing string

Full size image

Studies on the sealing properties and optimization of the structural parameters of packer rubber through theoretical calculation, numerical simulation and experimental verification are being done. For theoretical calculation, Al-Hiddabi et al. (2015), Al-Abri et al. (2015), Renaud et al. (2009) investigated the deformation of an elastomer seal confined between a metal tube and a rigid casing. They showed the effect of the geometry of the elastomer geometry and its material properties on sealing performance in terms of maximum sealing pressure. Alkharusi et al. (2011), Gajewski et al. (2015), Akhtar et al. (2018) investigated the effects of the material and geometrical properties of the elastomer on its sealing performance under different loading conditions. In addition, they investigated the effect of radial strain and annular fluid pressure on the sealing performance. Agata et al. (2013) described the material and form factors that regulated the ability of the pipe to expand. These factors included the influence of axial restraint during expansion and the post-expansion collapse resistance of solid expandable tubulars. Banks et al. (2002) studied the compression of rubber bonded to rigid metal plates of different geometry (rectangular and V-shaped blocks). Zhang and Wang (2016), Zhang et al. (2018) while relying on the laws of momentum and energy conservation and the transient heat transfer property between the wellbore fluid and the annulus fluid developed a calculation model of the temperature and pressure fields on single-layer and multi-layer annuli. Cavalaro and Aguado (2012) characterized the behavior of the packer under simple stress (normal) and under coupled stresses (normal and tangential) as well as proposed mathematical constitutive models to describe both behaviors. Their results indicated that the packer presented a nonlinear almost elastic mechanical behavior from the second load cycle onwards. For numerical simulation, Hu et al. (2017, 2018), Patel et al. (2019a, b) studied the influence of three rubber materials on sealing performance of packing element in the compression packer. Wang et al. (2017), Lan et al. (2019) studied the structure of the packer rubber with different materials and optimized the structure of its sealing unit. Based on the simulation results, the best inner groove shape and the structure of shoulder protection were confirmed. Furthermore, the validity of the simulation results was experimentally confirmed. Xu et al. (2017) investigated the structural response of tubulars to stress evolution, deformation of the thread joint and to the effect of expansion cone geometry. It was found that both the axial and hoop compressive stress concentrations were generated in the thread teeth edges near the contact surfaces of threads. This was associated with the mutual squeezing of box and pin thread teeth during experimental verification. Qamar et al. (2009), Al Ramadan et al. (2019), Daou et al. (2014) mechanically tested and characterized an inert water-swelling elastomer that had been developed by a local petroleum development firm. The elastomer was tested for hardness, compression at different temperatures and for different periods of time, tensile strength at different strain rate, tensile properties regarding fracture strength and percent elongation, and swelling ratio. Ahmed et al. (2019a, b), Al Ramadan et al. (2019) performed the verification process and tests by critically reviewing the literature, current regulations, and applicable industrial standards in order to develop testing protocols for the investigation of the performance of common elastomeric seals that are used in a liner hanger seal assembly. Dong et al. (2020), Fothergill (2003) determined seal failures of the rubber tube at high temperatures and studied the constitutive model parameters of the rubber tube through the rubber thermal aging experiments. The effects of key parameters of the rubber tube-casing gap, the dip angle of the adjacent rubber tube contact surface, and the initial setting load on the sealing performance of the packer under high temperature conditions were analyzed. Chen et al. (2019), Grelle et al. (2019) determined the effects of different stress conditions and the speed of lifting or lowering the pipe on the weakness of the rubber matrix.

The above described studies determined contact stress distribution of the rubber cylinder under different structural parameters, and optimized the rubber structure with the maximum contact stress as the goal. However, the tearing failure caused by excessive internal stress of the rubber was not considered. These studies did not consider the effect of cord arrangement parameters on the performance of the rubber. This resulted in large variations between the simulation results and the actual condition. In addition, the optimization method utilized the maximum contact stress as the single optimization goal and ignored the internal failure stress. This could not improve the overall performance of the expandable packer. In this paper, the numerical simulation model of nylon cord packer was established by considering the inner cord action of the drums. With the aim of sealing performance and pressure-bearing performance, a combination of response surface method and a genetic algorithm were used to optimize the design of nylon cord rubber. Specifically, the Plackett–Burman test was used to determine the climbing direction of influencing factors. The steepest climbing test was used to obtain the center of the response surface. The response surface method was used to acquire the polynomial response surface model connecting the cord angle, the number of cord layers and the cord spacing with bearing and sealing performance. Optimal structural parameters of the nylon cord rubber were determined according to the requirements of field operations. To meet the high-pressure and fine fracturing on-site use requirements, the reliability of the optimized results was verified by laboratory tests.

2 Structure and analysis method

2.1 Structure of nylon cord rubber tube

The nylon cord packer is shown in Fig. 2. It is composed of the upper joint, upper steel bowl, vulcanized core, central tube, rubber cylinder, lower cylinder liner and lower joint. At work, the expansion fluid was pumped into the nylon cord packer rubber from central tube through the ground booster pump. When the pressure difference between the internal and external oil pipes reached the packer starting pressure, the rubber tube expanded. After the pressure was relieved, the packer barrel automatically shrank to complete the unsealing by depressurizing the ground.

Fig. 2
figure 2

Structure diagram of the downhole expandable packer. 1-upper joint; 2-upper steel bowl; 3-screw; 4-plug nail; 5-vulcanized core; 6-central tube; 7-cylinder; 8-vulcanized core; 9-cylinder liner; 10- Piston; 11-lower cylinder liner; 12-”O” seal; 13-lower steel bowl; 14-lower joint

Full size image

The tearing failure under excessive setting pressure and sealing failure caused by low contact pressure of the expandable packer were common reasons for failure. To enhance the total working performance, we improved the bearing pressure and sealing pressure of the expandable packer. The bearing pressure represented the ultimate setting pressure before packer failure which can expand the packer and encapsulate the annular space between the casing and the center pipe. At the same time, the sealing performance of the expandable packer depended on the contact pressure. Increasing the contact pressure enhanced the sealing performance. When analyzing the expandable packer, the maximum contact pressure along the sealing surface was considered to be the sealing pressure under the setting pressure. The working condition of the expandable packer is shown in Fig. 3.

Fig. 3
figure 3

The working condition of expandable packer

Full size image

In order to improve the bearing pressure and sealing pressure, the nylon cord rubber adopted the nylon cord as skeleton, which was composed of an inner and an outer rubber. The structural parameters of the nylon cord rubber used in the oilfield are shown in Table 1. Laboratory tests indicated that the maximum set pressure of the current expandable packer was 60 MPa and the maximum sealing pressure was 30 MPa. These pressures could not meet the site requirements of low-permeability oil and gas reservoirs with a set pressure of 70 MPa and a sealing pressure of 50 MPa. Therefore, the parameters of cord arrangement and barrel structure should be optimized.

Table 1 Structure parameter of nylon cord packer
Full size table

2.2 Establishment of the finite element model

The finite element model of the nylon cord rubber is shown in Fig. 4. Due to the symmetry of expandable packer, a quarter of the three-dimension finite element model was developed with the Y-axis as the symmetrical axis. The SOLID185 element was used for the plastic tube, center tube, sleeve, and upper and lower joints while the REINF265 element was used as the polyamide cord reinforcement material. The 70 MPa setting load was applied inside the expandable packer. According to the indoor material test (ASTM D573-04 2015), the material parameters of nylon cord rubber cylinder are shown in Table 2 (Wang et al. 2020).

Fig. 4
figure 4

Nylon cord rubber finite element model

Full size image
Table 2 Material parameters of nylon cord rubber
Full size table

In terms of material failure, the third strength and maximum stress criteria were utilized for stress analysis of expandable packer in formula (1). In particular, shear failure was common inside the expandable packer. The third strength criterion states that the plastic flow occurs when the maximum shear stress reaches its shear strength. This phenomenon was attributed to the failure mechanism of the rubber. The maximum stress criterion which states that material damage occurs when the maximum stress stretches to the tensile strength was associated with damage to the fiber. According to the above material criteria, the different parameters of nylon cord rubber were optimized to meet the site use requirements of low-permeability oil and gas reservoirs (70 MPa setting pressure and 50 MPa sealing pressure).

2.3 Optimal design test methods

Because the response surface model has a high fitting accuracy in the center neighborhood while the fitting accuracy outside the center neighborhood is low, the fitting equation was almost meaningless. Using the ANSYS software, the Plackett–Burman test was used to screen for key factors, the steepest climbing test was applied to approximate the best area, and a polynomial model connecting the influencing factors with pressure resistance and contact performance of the nylon cord rubber was established by response surface method.

2.3.1 Plackett–Burman Test Design

During field investigations, the cord angle, the number of cord layers, cord spacing, the end inclination angle, and the thickness of the barrel were the test factors. Each test factor was taken at two levels for the test design. The high level was marked (+ 1). The low-level mark was (− 1). The optimal level of each factor was determined and the key factors selected. The Plackett–Burman test parameter design is shown in Table 3.

Table 3 Plackett–Burman test design
Full size table

2.3.2 The Steepest Climbing Test Design

The steepest climbing test design utilizes the direction of the gradient of the test value as the climbing direction. It determines the step size of the change according to the effective value of each factor, which can quickly and economically approach the optimal response area. During the test, and based on Plackett–Burman test results, the design direction of the influencing factors was changed, and the steepest climbing test of the pressure resistance performance Pmax and sealing performance Cmax of the nylon cord rubber was determined.

2.3.3 Response Surface Test Design

The response surface test was designed by experimenting on a set of sample points in a specified design space. The global approximation function of the system can be approximated to replace the actual response surface. In an engineering optimization design, the response relationship between the response target and the design variables can be achieved through the response surface test, and the design variables under the optimal objective function can then be determined.The second-order polynomial model is often the construction of the response surface approximation model. The approximation is the relationship between the system input and the response target. The basis function is shown in formula (1):

$${\text{y }} = \beta_{0} + \sum\limits_{i = 1}^{k} {\beta_{i} x_{i} } + \sum\limits_{i = 1}^{k} {\beta_{ii} x_{i}^{2} } + \sum\limits_{{\frac{i = 1}{i < j}}}^{k} {\beta_{ii} x_{i} x_{j} }$$
(1)

whereby β is the interaction coefficient between offset, linear offset and second-order offset; k is the total number of design variables; Y is the predicted response value.

Box-Behnken Design (BBD) is a common test design method for response surface testing. The number of tests is compact, and the economy is good. It is suitable for optimization experiments with 2 to 5 factors. Each factor takes 3 levels, with 0 as the center point, (+ 1) and (− 1) are the high and low values corresponding to the cubic points, respectively. The independent variables are coded according to formula (2). The distribution of test points is shown in Fig. 5 while the design of response surface test parameters is illustrated in Table 4.

$$X_{i} = (x_{1} - x_{0} )/\Delta x$$
(2)

whereby Xi is the encoding value of independent variable, x1 is the true value of the independent variable at the test center point, and Δx is the step size of the independent variable.

Fig. 5
figure 5

Flow chart of multi-objective genetic algorithm

Full size image
Table 4 Response surface test design
Full size table

2.3.4 Genetic Algorithm Optimization

Genetic algorithm is a type of adaptive artificial intelligence technology that simulates the evolutionary processes of biological organisms and the solution of extreme values. Its basic idea is an algorithm that searches for the optimal solution formed by simulating the genetic mechanism of nature and biological evolutionary theory. It is suitable for solving complex nonlinear and multidimensional optimization problems. Multi-objective genetic algorithm, as a fast and effective global optimization algorithm, has a brisk running speed. The solution set has the advantage of excellent convergence. The specific optimization process was as shown in Fig. 5.

2.4 Laboratory test

To verify the accuracy of the simulation results, indoor tests of the nylon cord rubber before and after the optimization were performed. The dimensions of the experimental setup and the simulation model were consistent, and the specific constitution of the experimental setup was as follows: (1) Packer experimental rig including 51/2 casing (with an outer diameter of 139.7 mm), 27/8 tubing (with an outer diameter of 78.6 mm), flange and plug hear; (2) K344-114 expansion packer on which a rubber be can installed; (3) High-pressure pumps (100 MPaand 60 MPa); (4) Oil bath device and pipe line (Wang et al. 2020). The schematic diagram of the laboratory test setup was as shown in Fig. 6, and the process of experimental measurement was as shown in Fig. 7. Briefly, the rubber was assembled on the expandable packer with an amount of butter being applied on the sealing groove and engine oil being applied on the surface of the thread. The lower end of the packer was then connected with blind plugging to block its outlet. The entire expandable packer was soaked in water at 18–28 °C for 24 h. It was then installed in the casing. The pressure pump (100 MPa) was connected to the center pipe through the center pipe sealing cover while the pressure pump (60 MPa) was connected with an annular between the casing and tubing through the casing sealing cover. The pressure gauges of the center and casing pipelines were set and used to observe the working conditions of the expandable packer. In addition, the casing valve was closed and the center pipe valve opened. The high-pressure liquid was driven through the high-pressure pump (100 MPa) into the center pipe. After pressing the inside packer within a pressure range of 0–80 MPa and stabilizing the pressure for 5 min every 10 MPa, the working conditions of the packer could be observed. If the pressure gauge in tube pipeline rose steadily and remains steady for 5 min, the pressure test pump continued to exert pressure based on the existing pressure. When the pressure gauge experienced a rapid decline with sharp fluctuations, the pressure test pump stopped and the packer was considered to have been damaged. The maximum setting pressure before packer failure during the period of pressure stabilization was known as the bearing pressure. After pressing the packer from the center pipe at 10 MPa to the bearing pressure, the center pipe valve was closed and the casing valve opened. The sealing pressure under different setting pressures was measured. To be specific, the high-pressure liquid was driven through the high-pressure pump (60 MPa) into the annulus between center pipe and casing from 5 to 60 MPa for 5 min every 5 MPa. If the pressure gauge in the casing pipeline rises steadily and remains stead for 5 min, the pressure test pump continued to exert pressure based on the existing pressure. When the pressure gauge experienced a rapid decline with sharp fluctuations, the pressure test pump was stopped and the packer was considered to have been damaged. The maximum annual working pressure before packer failure during the period of pressure stabilization was shown in the pressure gauges in casing pipeline. It was described as the sealing pressure under the setting pressure. After the test, pressure was released and the packer was restored to its original state. The failure morphology of expandable packer was observed.

Fig. 6
figure 6

Laboratory equipment layout diagram

Full size image
Fig. 7
figure 7

Polyamide cord rubber test diagram

Full size image

3 Results and discussion

3.1 Plackett–Burman test results

The Plackett–Burman test results are shown in Table 5. The diagrammatic presentation of the Pareto standardization effect of pressure-bearing performance is shown in Fig. 8. The number of cord layers exhibited a positive effect while the cord angle, cord spacing, end face inclination, and packer thickness exhibited negative effects. The influential order of each factor on the pressure-bearing performance was: cord angle > cord layer > cord spacing > rubber thickness > shoulder angle. From the Pareto chart of the standardization effect of the sealing performance, it can be seen that the cord spacing and shoulder angle exhibited positive effects while the cord angle, cord layers and shoulder angle exhibited negative effects. The influential order of each factor on sealing performance was: cord layer > cord angle > cord spacing > rubber thickness > shoulder angle.

Table 5 Plackett–Burman test results
Full size table
Fig. 8
figure 8

Pareto diagram of the normalized effect of impact factors

Full size image

Above all, it can be seen that nylon cord parameters (cord angle, cord layer and cord spacing) exerted a more obvious effect on bearing pressure and sealing pressure when compared to rubber parameters (rubber thickness and shoulder angle). This could be attributed to the fact that nylon cord was the frame of expandable packer on which the external pressure was exerted. In addition, changes in cord angle, cord layer and cord spacing played a significant role in bearing pressure and sealing pressure. Therefore, we determined the influence of nylon cord arrangement on the bearing pressure and sealing pressure of the expandable packer and other factors were in agreement with the site. It can be found that with an increase in cord angle, the radial stiffness of the rubber grew. This led to cord breakage and low sealing pressure that resulted to poor bearing pressure. Meanwhile, as the cord layer increased, the vertical stiffness of the packer grew synchronously. This improved the bearing pressure. Considering the high vertical stiffness, the sealing pressure roughly reduced under the same setting pressure. Furthermore, the bearing pressure experienced a reduction when the cord spacing grew due to lower vertical stiffness of the nylon cord in the expandable packer. In contrast, it improved the sealing pressure. In field practice, the cord angle and the cord space should be reduced. To ensure pressure performance, few cord layers should be selected.

3.2 The steepest climbing test results

These results are shown in Table 6. It is shown that the pressure-bearing performance Pmax and sealing performance Cmax of Test 4 met the site requirements. However, before Test 4, the pressure-bearing performance Pmax was lower compared to the field setting pressure. After Test 4, the seal performance Cmax of the cartridge was lower compared to the field sealing pressure. Therefore, optimal structural parameters were obtained between Tests 3 and Test 4, and the response areas of the cord angle, the number of cord layers, and the cord spacing were [17, 18], [6, 8], and [1.7, 1.8], respectively.

Table 6 The steepest climb test parameters
Full size table

3.3 Response surface test results

On the basis of the corresponding surface method, the Minitab software was used to generate a test plan table and record the test results for each group of factor combinations as shown in Table 7. The experimental data were fitted by polynomial regression analysis to determine the effects of the independent variables (X1, X2, X3) on pressure performance Pmax. The polynomial response surface model is given as follows:

$$\begin{aligned} P_{ \text{max} } & = - 175 + 27.7X_{1} + + 29.01X_{2} - 101X_{3} - 0.736X_{1}^{2} \\ & \quad - 2.1354X_{2}^{2} + 27X_{3}^{3} + 0.038X_{1} X_{2} - 1.821X_{1} X_{3} + 3.07X_{2} X_{3} \\ \end{aligned}$$
(3)
Table 7 Plackett–Burman test result table
Full size table

The results of the analysis of variance are shown in Table 8, F = 1158.98 > F0.01 (9,7) = 6.72, Pr > F < 0.001. The regression model in which the linear and square effects were obvious is shown to be highly significant. The coefficient of determination is R = 99.85% indicating that 99.85% of the data can be interpreted by this model, while 0.15% of the variance values cannot be interpreted by this model. This shows that the actual measured value was highly correlated with the predicted value, and the model had a high accuracy.

Table 8 Results of variance analysis of pressure-bearing performance
Full size table

The test data were fitted by polynomial regression analysis to determine the effect of the independent variables (X1, X2, X3) on the seal performance Cmax. The polynomial response surface model is given as follows:

$$\begin{aligned} C_{ \text{max} } & = 67 - 0.62X_{1} - 6.07X_{2} + 27.7X_{3} - 0.296X_{1}^{2} \\ & \quad + 0.2229X_{2}^{2} - 38.2X_{3}^{3} + 0.0262X_{1} X_{2} + 6.08X_{1} X_{3} \\ & \quad - 0.019X_{2} X_{3} \\ \end{aligned}$$
(4)

The results of the analysis of variance are shown in Table, F = 1147.95 > F0.01 (9,7) = 6.72, Pr > F < 0.001. The model is highly significant. The linear and square effects were obvious. The coefficient of determination was R = 99.85%. This illustrated that 99.85% of the data could be interpreted by the model.

As shown in Table 9, the interaction term X1X3 exhibited a significant effect on the pressure-bearing performance. To determine the influence of the changing trend of influencing factors and their interactions on contact stress, the number of cord layers was taken as the center level. The contour map of the other two factors was drawn according to the regression Eq. (4).

Table 9 Variance of sealing performance
Full size table

In general, high contact pressure represented the better sealing performance of expandable packer. During parameter optimization, the structure with high sealing pressure should be selected. The influence of the cord angle is shown in Fig. 9. As the cord angle increased, contact pressure initially increased and then reduced. At 18°, contact pressure was high, representing a better sealing performance. Reduction in cord spacing led to an increase in contact pressure. The high contact pressure reached a plateau when the cord angle was nearly 18° while the cord spacing was about 15°. There was an “isolate land” when the cord angle was nearly 20° and the cord spacing was about 16.l°.

Fig. 9
figure 9

Cord angle and cord spacing contour map

Full size image

3.4 Genetic algorithm optimization results

With the nylon cord rubber pressure-bearing performance and sealing performance as optimization targets, and cord angle, cord layer and cord spacing as variables the model was transformed into the minimum problem of solving functions (−Pmax) and (−Cmax). The optimization proposition can be expressed as:

$$\begin{array}{*{20}l} {} \hfill & {\hbox{min} \;\left( { - P_{\text{max} } } \right)} \hfill \\ {} \hfill & {\hbox{min} \;\left( { - C_{\text{max} } } \right)} \hfill \\ {{\text{s}} . {\text{t}} .} \hfill & {P_{\text{max} } \ge 70} \hfill \\ {} \hfill & {C_{\text{max} } \ge 50} \hfill \\ {} \hfill & {0 \le X_{1} \le 45} \hfill \\ {} \hfill & {0 \le X_{2} \le 8,\;X_{2} = 2n,\;n \in Z + ;} \hfill \\ {} \hfill & {0 \le X_{3} \le 3} \hfill \\ \end{array}$$
(5)

When the multi-objective genetic algorithm was optimized, the population number was 50, the evolution number was 80, the crossover probability was 0.8, and the mutation probability was 0.1. The results show that in the evolution of 55 generations, the Pareto optimal solution was obtained. According to the actual working parameters at the site, when the set pressure was 70 MPa and the sealing pressure was 50 MPa, the pressure and sealing performance of the rubber met the requirements for use. At a cord angle of 16°, 6 cord layers, and a cord spacing of 1.6 mm, the best solution from the best area of Pareto and the optimal parameters of the nylon cord rubber could be acquired. These results are shown in Fig. 10.

Fig. 10
figure 10

Multi-objective genetic algorithm optimization results

Full size image

3.5 Design Analysis of results before and after optimization

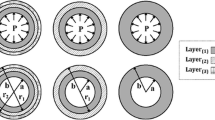
Figure 11 shows changes in nylon cord and rubber cord arrangement before and after optimization. Figure 12 shows changes in stress and contact stress of the nylon cord rubber before and after optimization. Figure 9 shows that as the sealing pressure increased, rubber stress and contact stress increased simultaneously. After optimization, the rubber stress significantly reduced while the contact stress significantly increased. This was conducive for improving the rubber service life and working reliability. Compared to the rubber material, the inner cord of the rubber exhibited a significant stress concentration that was prone to strength failure. This outcome was used to ascertain the pressure-bearing performance of the nylon cord rubber. This indicates that the pressure-bearing capacity of the optimized rubber was gradually enhanced, resulting in the increase in cord stress and the decrease in rubber stress.

Fig. 11
figure 11

Comparison of structural parameters before and after optimization

Full size image
Fig. 12
figure 12

Changes in stress and contact stress of nylon cord rubber before and after optimization

Full size image

By comparing and analyzing the working performance of the nylon cord rubber before and after optimization, the pressure-bearing performance of the drum after optimization was 75 MPa. This was a 25% increase compared to the pressure-bearing performance before optimization. The sealing performance of the drum after optimization was 57.5 MPa. This was a 66% in the sealing performance that was observed before optimization (34.5 MPa).

3.6 Results verification

3.6.1 Response Surface Model Verification

The ANSYS software was used to establish a three-dimensional mechanical finite element model based on the structural parameters of the nylon cord rubber. The pressure-resisting performance of the rubber after optimization and the sealing performance of the drum under a 70 MPa setting pressure was analyzed. The obtained results and the response surface model (3) and (4) results were compared to verify the accuracy of the response surface model (Table 10). The results indicated that the response surface model was similar to the ANSYS simulation results, and the error was within 10%.

Table 10 Response surface model validation
Full size table

3.6.2 Laboratory Test Verification

Figure 13 shows that the increase in sealing pressure was directly proportional to the increase in setting load. For the pre-optimized rubber, the bearing pressure of the packer was 60 MPa while the sealing pressure of the packer was 30 MPa. For the optimized rubber, the bearing pressure of the post-optimized cartridge was 70 MPa while the sealing pressure was 50 MPa. The error was within 40% as shown in Fig. 14. The test results show that the optimized nylon cord rubber effectively complied with the requirements of low-permeability oil and gas reservoirs with a 70 MPa setting pressure and 50 MPa sealing pressure.

Fig. 13
figure 13

Rubber simulation versus experiment comparisons before and after optimization

Full size image
Fig. 14
figure 14

The error percentage of sealing performance before and after optimization

Full size image

4 Conclusions

A novel numerical simulation and optimization method was used to evaluate the performance of the expandable packer. To meet the requirements of high-pressure and fine fracturing, the reliability of the optimized results was verified by laboratory tests.

  1. 1.

    Using the field packer as an example, a REFINE265 unit was applied in a three-dimensional numerical simulation model of the nylon cord rubber. The maximum pressure performance of the cartridge was 60 MPa while the maximum sealing performance was 30 MPa. The simulation results were consistent with the test results. These outcomes verified the accuracy of the simulation model.

  2. 2.

    Using Plackett–Burman test, steepest climbing test and response surface test, the multi-objective optimization of the nylon cord rubber was performed with the pressure-bearing and sealing performance as the objective functions. The accuracy of the response surface model obtained was superior simulated with ANSYS, which remains within 90%.

  3. 3.

    Based on the actual working parameters in the field, the optimal combination of nylon cord rubber tube structure parameters (the cord angle (16°), cord layers (6), and cord spacing (1.6 mm)) was determined. It was shown that the optimized rubber bearing pressure performance increased to 75 MPa. This was a 25% increase compared to the pre-optimized rubber. The sealing performance is increased to 57.5 MPa, which was a 66% increase compared to than that before.

  4. 4.

    The laboratory tests showed that the maximum set pressure of the barrel after optimization was 70 MPa while the maximum working pressure was 50 MPa. These outcomes effectively met the high-pressure and fine fracturing field requirements of low-permeability oil and gas reservoirs.