A simulation study comparing the Texas two-step and the multistage consecutive fracturing method

Abstract

Multistage hydraulic fracturing in horizontal wells is a critical technique for developing unconventional oil and gas resources. Stress interactions among neighboring fractures cause immature fracture development. The Texas two-step fracturing (TTSF) method is a new technique that aims to enhance fracture complexity and conductivity. This paper compares the fracture development of consecutive fracturing and the TTSF. The fracturing sequence in the multistage fracturing method has a significant effect on the fracture length, fracture width and injection pressure. The consecutive fracturing results in relatively uneven fracture length and width. Certain fractures in consecutive fracturing are restrained to be closed due to the strong stress shadowing effect. In contrast, TTSF has considerable potential for alleviating the negative effects of stress interactions and producing a larger stimulated reservoir volume.

1 Introduction

Due to tremendous energy demand, unconventional oil and gas resources have played a significant role in energy structures. To generate the maximum stimulated reservoir volume (SRV) of unconventional resources, multistage hydraulic fracturing technology associated with horizontal drilling technology is the most common method. The created hydraulic fractures (HF) connect the natural fracture system or induced-stress fractures, resulting in a complex fracture network (Olson 2008; Zhang et al. 2015). As a new technology in shale gas reservoir development, the network fracturing technology has attracted much attention in recent years. Oil-field engineers tend to stimulate shale gas reservoirs through multistage fracturing in horizontal wells; moreover, they also believe that multistage fracturing will create many complex fracture networks along a long wellbore (Li et al. 2017).

The main objective of multistage fracturing is to contact the reservoir by separating the long wellbore into many segments and creating many transverse fractures in each well segment. Optimizing fracture spacing and maximizing fracture length are critical methods for improving hydraulic fracturing treatment. However, the stress shadowing effect (Bunger et al. 2012; Morrill and Miskimins 2012), which is defined as the induction of an additional stress field by open fractures, negatively affects fracture widths and non-uniform fracture developments. Certain perforation clusters have not been proven to contribute to well production because their fracture lengths and widths are both restrained by neighboring fractures (Wu and Olson 2014; Long et al. 2018). Flow resistance, perforation friction, limited-entry effect, stage spacing, fracture spacing, etc., should be controlled to alleviate the negative effect of stress shadowing among simultaneously growing fractures (Wu et al. 2017; Long and Xu 2017). The simplest way to alleviate the stress shadowing effect is to reduce the perforation set number of each well segment, but this approach leads to a lower well production rate (Jo 2012; Soliman et al. 2008). Some researchers have proposed simultaneous hydraulic fracturing in multilateral horizontal wells to make full use of the stress shadowing effect (Sesetty and Ghassemi 2015). Another way to alleviate the stress shadowing effect is to optimize the stage sequence, stage spacing and perforation set spacing. Due to the limitations of current downhole tools, multistage fracturing is often conducted consecutively, stage by stage from the well toe to the well heel (Roussel and Sharma 2011; Xia et al. 2016). Each stage usually contains several perforation sets, and thus, several fractures propagate competitively if each perforation set produces only one fracture (Wu and Olson 2014). Microseismic monitoring in the field has proven to be highly effective in many engineering cases (McClure 2012). Cheng et al. (2017a) presented a model for simulating multistage consecutive fracturing that first considers the fracture closure behavior after pump shutoff. Furthermore, the fracture geometry in the subsequent stage is also affected by the stress shadowing induced by the fractures created in the previous stages (Cheng et al. 2017b). The stress shadowing effect decreases with increasing stage spacing (Cheng 2012) and increases with the injection rate and viscosity of the fracturing fluid.

Rafiee et al. (2012) presented a modified zipper frac in which fractures are initiated in a staggered pattern. The authors adjusted the fracturing sequence in adjacent parallel horizontal wellbores to enhance hydrocarbon production. In contrast to multistage consecutive fracturing in one horizontal wellbore, Soliman et al. (2010) and Roussel and Sharma (2010) proposed the Texas two-step fracturing (TTSF) method to minimize fracture interference in the minimum horizontal stress direction and enable relatively even fracture development. The second step of multistage consecutive fracturing is placed within the first step of multistage consecutive fracturing. TTSF is an alternative fracturing strategy that requires a special downhole tool. Based on a well-established model (Cheng et al. 2017a), this article simulates the fracture propagation of TTSF and investigates the produced fracture geometry. This paper demonstrates some benefits of TTSF. It may be worth developing a special downhole tool for the application of TTSF.

2 Texas two-step fracturing method

In contrast to vertical wellbore fracturing, a long horizontal wellbore is usually divided into several segments, and the wellbore is fractured stage by stage. Due to the limitations of current downhole tools, the most popular multistage fracturing method used in the fields is carried out consecutively (Fig. 1), moving from the wellbore toe to the wellbore heel (Roussel and Sharma 2010). The wellbore toe represents the bottom of the wellbore. Each segment usually includes one or more perforation sets. It is often assumed that each perforation set produces only one main fracture (Wu and Olson 2014).

Fig. 1

Sketch of multistage consecutive fracturing (Cheng et al. 2017a)

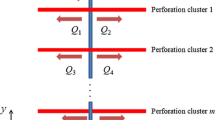
Due to the stress shadowing effect around the open fracture, a hydraulic fracture (HF) in a subsequent stage is strongly affected by the HF in the previous stages unless the stage spacing is sufficiently large. After the first step of consecutive fracturing, the horizontal wellbore could theoretically be stimulated in the second step of consecutive fracturing, which consists in placing the perforation cluster within the stage interval of the first step (Fig. 2). This completion method is usually called TTSF, although its applications are limited by the currently available downhole tools. The stage spacing between stages 1 and 2 in TTSF is twice as large as that in the traditional multistage consecutive fracturing. When the stage spacing increases, the negative effects of stress shadowing will decrease. By fracturing in two steps and thus increasing the distance between two subsequent fractures, TTSF reduces the negative effects of stress shadowing and allows for a greater stimulated reservoir volume.

Fig. 2

Texas two-step fracturing method

The stress interactions induced by the HFs in the first step (blue fractures in Fig. 2) create a low stress anisotropy area. Stage k + 1 takes advantage of the low stress anisotropy induced by the HFs in stages 1 and 2 (Fig. 2). Stage k + 2 takes advantage of the low stress anisotropy induced by the HFs in stages 2 and 3 (Fig. 2). Therefore, the hydraulic fracturing technique in the second step has considerable potential to create secondary fractures. TTSF provides a new possible strategy and is an interesting choice for unconventional oil and gas reservoir stimulations, although the secondary fracture network has not been rigorously tested in the laboratory.

Although the mechanical problems associated with multistage fracturing are highly complex, the basic mechanical model of multistage fracturing is one-stage multiple-fracture propagation. The multiple-fracture propagation model was verified and presented in detail in a recently published article (Cheng et al. 2017a). The model couples the fracture opening, stress interaction, fluid flow inside fractures and Carter’s leakoff using the Picard iteration method. Fracture closure behavior after pump shutoff is considered according to the proppant used and stress shadow induced by the neighboring fractures. This article mainly focuses on the benefits of the TTSF method and its comparison with consecutive fracturing instead of formula derivation. Therefore, only a brief introduction to the numerical model is provided in “Appendix.”

3 Single propagating fracture in one stage

All cases considered in this article use the same input parameters and mechanical model reported in a previous article (Cheng et al. 2017a). A horizontal well is drilled along the direction of the minimum horizontal stress (σ_h). The numerical model inputs are presented in Table 1. The fracture or perforation set spacing is 30 m in consecutive fracturing. The fracture spacing is 60 m in TTSF because the second step of the multistage consecutive fracturing is placed within the first step of multistage consecutive fracturing. Hence, the positions of the perforation set in the consecutive fracturing and TTSF are coincident to enable a comparison of their fracture geometries. The only difference between the two methods is the sequence of the fracturing process and the stress interaction among the fractures.

Table 1 Input parameters (Cheng et al. 2017a)

3.1 Consecutive fracturing

If each segment of a borehole is perforated with only one perforation set and each perforation set produces only one main fracture, the HFs will propagate sequentially in the multistage consecutive fracturing technique (Sesetty and Ghassemi 2015). The fluid pressure decreases along the HF length (Fig. 3a) because of flow pressure drops inside the fracture. However, the fluid pressure of the subsequent HF is slightly higher than that in the previous HF, although the HF length and fracture spacing are uniform. In fact, the fluid flow inside the fracture and the fracture opening are not independent during the hydraulic fracturing process. The fracture opening and fracturing fluid flow represent a coupled mechanical problem. Cheng et al. (2017a) solved this coupled problem using the Newton–Raphson iteration method. The fracture width decreases along the HF length (Fig. 3b), which agrees well with the KGD model (Khristianovic and Zheltov 1955; Geertsma and de Klerk 1969). The fracture geometry is similar for all HFs because the fracture length of each HF is controlled by setting the number of propagation steps and injection time. The first fracture is straight due to the undisturbed far-field in situ stress (Fig. 3). The second fracture is slightly deviated from the first fracture due to the redistributed stress field induced by the first fracture. All the subsequent fracture paths are slightly deviated from the previously created fractures. Therefore, the fracture geometries of Fracs 2, 3, 4, 5 and 6 are very similar.

Fig. 3

Fluid pressure and fracture width distributions in consecutive fracturing

The fluid pressure at the fracture tip is usually equal to the minimum horizontal stress (σ_h) because the HF must open against the least in situ stress. The injection pressure at the bottom hole is equal to the sum of σ_h and the flow resistance along the fracture channel. Although the HF length increases, the fracture width will become wider and the flow resistance will then decrease sharply because of the cubic law obeyed by channel flow. The injection pressure decreases with the injection time and approaches a minimum horizontal stress (Fig. 4). Compared with the injection pressures in each HF, the injection pressure in the subsequent HF is slightly higher than that in the previous HF. The pressure difference between Fracs 1 and 2 is higher than that between Fracs 2 and 3. The results in Fig. 4 agree well with the fluid pressure distribution in Fig. 3a. The subsequently created fracture (Frac i + 1) must suffer the cumulative stress shadowing effect induced by all the previously created fractures (Fracs 1 − i). The stress shadowing induced by the neighboring fracture is computed using Eq. (11) in “Appendix.” Therefore, the injection pressure relationship is Frac 1 < Frac 2 < Frac 3 < Frac 4 < Frac 5 < Frac 6 in this case, as shown in Fig. 4.

Fig. 4

Injection pressure at the well bottom versus injection time in consecutive fracturing

3.2 Texas two-step fracturing

The wellbore is divided into two steps of consecutive fracturing (Fig. 2). The perforation sets of the second step (Fracs 4, 5 and 6) are placed within the first fracturing step (Fracs 1, 2 and 3). Using the input parameters presented in Table 1, the fracture propagation is simulated according to the mechanical model described in “Appendix.” When the fracture propagates to a target length, the fluid pressure and fracture width are recorded. After all 6 fractures reach the target length, the fluid pressure and fracture width distribution of TTSF are demonstrated in Fig. 5. The fluid pressure in the fractures of the second step is higher than the pressure in the first step (Fig. 5a). The fracture width in the second fracturing step is smaller than that created in the first fracturing step (Fig. 5b), indicating that the HF created in the second fracturing step must open against a higher confining pressure. The confining pressure consists of the in situ stress and the stress shadowing induced by the previously created HFs. The fluid pressure and width distributions in Fracs 2 and 3 are similar. Furthermore, the fluid pressure and width distributions in Fracs 4 and 5 are similar. It is easy to envision that Fracs 2, 3, …, k are similar and Fracs k + 1, k + 2, …, 2k − 1 are similar if the total fracture number is 2 k in Fig. 2.

Fig. 5

Fluid pressure and fracture width distribution in TTSF

Compared with the injection pressures in each HF, the injection pressure at the well bottom in the second fracturing step (Fracs 4, 5 and 6) is higher than that in the first fracturing step (Fracs 1, 2 and 3), as shown in Fig. 6. This pattern indicates that it is more difficult to inject fluid into the HF in the second step of consecutive fracturing. The main reason is the stress shadowing (Fig. 7) induced by the first step of fracturing. The stress field in Fig. 7 is quantified by Eq. (11) in “Appendix.” The basic method represented by Eq. (11) is the boundary element method (Crouch and Starfield 1983), which can compute the displacement discontinuity on the fracture surface and the solid deformation in the matrix. Each fracture has two surfaces. The left surface of Frac 4 suffers the stress shadowing induced by Frac 1, while the right surface of Frac 4 suffers the stress shadowing induced by Fracs 2 and 3. The left surface of Frac 5 suffers the stress shadowing induced by Fracs 1, 4 and 2, while the right surface of Frac 5 suffers only the stress shadowing induced by Frac 3. In contrast, only the left surface of Frac 6 suffers the stress shadowing induced by Fracs 1–5. Therefore, the injection pressure relationship is Frac 1 < Frac 2 < Frac 3 < Frac 6 < Frac 4 < Frac 5 in this case (Fig. 6).

Fig. 6

Injection pressure at the well bottom versus injection time in TTSF

Fig. 7

Stress shadowing induced by the first step fracturing. ‘+’ represents compressive stress

3.3 Comparison of fracture geometry

Note that the perforation set positions in Figs. 3 and 5 are the same. The only difference between the consecutive fracturing method and TTSF is the sequence of the perforation sets. The paths of the fractures are shifted from left to right according to the x-coordinates (Fig. 8). Fracs 2–3–4–5–6 in consecutive fracturing are compared with Fracs 4–2–5–3–6 in TTSF. Because all the fractures are symmetrical along the wellbore, only half of the fracture paths are presented in Fig. 8. All HFs created from perforation sets deviate from the minimum principal stress except for Frac 1 because this fracture opens against the in situ stress, and the other HFs must suffer the stress shadowing effects induced by Frac 1. The HF path in TTSF is straighter than that in consecutive fracturing, thus facilitating proppant movement.

Fig. 8

Comparisons of fracture paths in the two methods. CF represents consecutive fracturing

Figure 9 compares the maximum fracture widths. The fracture widths of TTSF and consecutive fracturing at positions $x = 0$ m and $x = 150$ m are similar. The maximum fracture width of the subsequent fracture in the consecutive fracturing decreases across the x-axis. The maximum fracture width in the second fracturing step of TTSF is smaller than that in the first fracturing step, implying that the proppant size in the second step should be designed to be smaller with respect to proppant migration. In the first step of fracturing, the width in Frac 2 ($x = 60$ m) and Frac 3 ($x = 120$ m) is larger than that in Frac 1 ($x = 0$ m). However, the maximum fracture width in consecutive fracturing gradually decreases with increasing fracture number. The reason is that the stress interaction decreases with the fracture spacing. The fracture spacing between Fracs 1 and 2 in the first step of fracturing is 60 m, while the spacing between Fracs 1 and 2 in consecutive fracturing is only 30 m.

Fig. 9

Comparison of the maximum fracture widths

4 Multiple propagating fractures in one stage

Three propagating fractures in each stage are taken as examples to demonstrate the fracture geometry in both TTSF and consecutive fracturing. The numerical model inputs are presented in Table 1. The fracture spacing is 30 m, and the stage spacing is 40 m in consecutive fracturing. The fracture/perforation set spacing is 30 m, and the stage spacing is 140 m in TTSF because the second step of multistage consecutive fracturing is placed within the first step of multistage consecutive fracturing. Three perforation sets are designed for each stage, and each perforation set is assumed to create only one fracture. Hence, the positions of the perforation set in the consecutive fracturing and TTSF methods are still the same.

4.1 Consecutive fracturing

If each stage of a borehole is perforated with several perforation sets at a time and each perforation set produces only one main fracture, multiple HFs will propagate simultaneously and competitively. As the fracture propagates to a target length, the fluid pressure and fracture width in each stage are recorded. The fluid pressure decreases along the HF length (Fig. 10a) because of the flow pressure drop. The fluid pressure inside the HF in the subsequent stage is also slightly higher than that in the previous stages. Stage 1 features two main fractures on two sides, which are much longer than the middle one. The reason is that the middle HF must suffer the strong stress shadowing induced by the side fractures. The middle HF is unlikely a main fracture. These three HFs in stage 1 are not affected by any previous stages because they are fractured first. The fracture width distribution in the subsequent stage is similar to the distributions in the second stages (Fig. 10b). The fracture geometry in the subsequent stage occurs periodically. The right fracture in the subsequent stage is the widest fracture and will grow to be a main fracture. Consecutive fracturing results in immature fracture development and uneven reservoir stimulation because of the strong stress interactions among the fractures in the same stage. The left two fractures in all subsequent stages are restrained to remain closed and may contribute to a small part of the well production. Note that Fig. 10 is similar to a figure reported in a previously published paper (Cheng et al. 2017a). The differences between the two are due to the fluid injection time in the corresponding figures.

Fig. 10

Fluid pressure and frac width distribution in consecutive fracturing

The variations of injection pressures are presented in Fig. 11. The injection pressure in each subsequent stage is slightly higher than that in the previous stages. However, the curves of Fracs 3–6 nearly overlap. The injection pressure relationship is still Frac 1 < Frac 2 < Frac 3 < Frac 4 < Frac 5 < Frac 6, which is similar to the results presented in Fig. 4. The reason is that the subsequently created fractures must suffer the cumulative stress shadowing effects induced by all the previously created fractures. A slight pressure fluctuation is observed in the first stage because of numerical instability in the solid–fluid coupling.

Fig. 11

Injection pressure at the well bottom versus injection time in multistage consecutive fracturing

4.2 Texas two-step fracturing

The fluid pressure and fracture width distributions of TTSF are presented in Fig. 12. The fluid pressure distributed inside the HF of the second fracturing step (stages 4, 5 and 6) is also higher than that of the first fracturing step (stages 1, 2 and 3). Stages 2 and 3 are similar, as are stages 4 and 5. It is easy to envision that stages 2, 3, …, k are similar, and stages $k + 1$, $k + 2$, …, $2k - 1$ are similar if the total stage number is 2 k in Fig. 2. Stages 1 and 6 in Fig. 12a are similar to those in Fig. 10a, respectively. There are two main fractures in the first step of fracturing, but only one main fracture in the second step of fracturing. The fracture length and width development in Fig. 12 is more uniform than that in Fig. 10, meaning that the reservoir will be stimulated to be more uniform in this case. Because the basic input parameters in Table 1 in TTSF and consecutive fracturing are the same, the difference in fracture geometry between the two fracturing methods is due to the fracturing sequence alone. When the fracture space is equal (Figs. 10 and 12), the SRV is linearly related to the fracture length. The total fracture length in consecutive fracturing (Fig. 10) is 384.5 m, while the total fracture length in TTSF (Fig. 12) is 450.4 m. The fracture length in TTSF is 17.1% longer than that in consecutive fracturing. TTSF has considerable potential to alleviate the negative effect of stress interactions and achieves a greater SRV than that of the consecutive fracturing method.

Fig. 12

Fluid pressure and fracture width distribution in TTSF

Normally, during the second step of fracturing in TTSF, several days will have passed since the end of the first step, but the stress shadowing effect will not diminish because of the proppant acting inside the hydraulic fracture. Compared with the injection pressure in each stage (Fig. 13), the injection pressure in the second step of fracturing is higher than that in the first step of fracturing. The injection pressure relationship is Frac 1 < Frac 2 < Frac 3 < Frac 6 < Frac 4 < Frac 5, which is similar to the relationship shown in Fig. 6. The explanation of this phenomenon is the same as that provided for Fig. 6.

Fig. 13

Injection pressure at the well bottom versus injection time in multistage TTSF

4.3 Comparison of fracture geometry

The input parameters for the rock and fracturing fluid properties in all numerical cases are the same. Furthermore, the perforation set positions and stage spacing in Figs. 12 and 10, respectively, are also the same. Stages 1–2–3–4–5–6 in consecutive fracturing are compared with stages 1–4–2–5–3–6 in TTSF. The maximum fracture widths are compared in Fig. 14, where the x-axis represents the perforation position. The fracture width distribution in TTSF is still highly complex but more uniform than that in the consecutive fracturing method. The maximum width of stage 1 is the same between TTSF and consecutive fracturing because of the same initial and boundary conditions. Although different boundary conditions are applied to stage 6, the maximum width of stage 6 is still similar between the two fracturing methods for the two following reasons. First, all previous stages (stages 1, 2, 3, 4 and 5) in both the TTSF and consecutive fracturing methods affect the stress field around stage 6. Second, the right side of stage 6 suffers only from far-field in situ stresses.

Fig. 14

Comparisons of the maximum fracture widths. CF represents consecutive fracturing

The maximum fracture width distribution in Fig. 14 is similar to the fracture width distribution in Figs. 10b and 12b. Only one fracture grows to be a main fracture in stages 2–5 of consecutive fracturing. In contrast, two fractures become main fractures in the TTSF method.

5 Conclusions

This paper simulates fracture propagation in the Texas two-step fracturing method and compares it with that in the consecutive fracturing method. The findings are as follows:

• (1) Comparisons of the injection pressures at each stage in consecutive fracturing show that the injection pressure in the subsequent stage is slightly higher than that in the previous stage. The injection pressure in the second step of the TTSF method is higher than that in the first step. In addition to the rock and fracturing fluid parameters, the fracturing sequence has a remarkable effect on the fracture length, fracture width and injection pressure.

• (2) The maximum fracture width distributions are similar to the fracture width distributions in both the TTSF and consecutive fracturing methods. Consecutive fracturing results in uneven reservoir stimulation, and certain fractures in the subsequent stages are restrained to be short and closed due to the negative effects of stress shadowing.

• (3) In contrast, the fracture length and width distributions in TTSF are more uniform than those in consecutive fracturing. Two main fractures are created in the second step of the TTSF method, but only one main fracture occurs in consecutive fracturing. TTSF has great potential to alleviate the negative effect of stress shadowing and allows for a greater SRV than that of consecutive fracturing. These benefits should encourage engineers to develop the special downhole tools necessary for TTSF to be applied in the field.

Appendix: a brief introduction to the model of multistage fracturing

Each HF is divided into N_k ($k = 1,\;2,3,\; \ldots ,\;M$) elements. Multiple HFs in one stage include N elements. The stress equilibrium equation of the element is given by the displacement discontinuity method (Crouch and Starfield 1983):

$$\left\{ {\begin{array}{*{20}l} {\sum\limits_{j = 1}^{N} {\left( {{\mathbf{A}}_{\text{ss}}^{ij} D_{\text{s}}^{j} + {\mathbf{A}}_{\text{sn}}^{ij} D_{\text{n}}^{j} } \right){ = } - \frac{1}{2}(\sigma_{\text{h}} - \sigma_{\text{H}} )\sin 2\theta_{i} } } \hfill \\ {\sum\limits_{j = 1}^{N} {\left( {{\mathbf{A}}_{\text{ns}}^{ij} D_{\text{s}}^{j} + {\mathbf{A}}_{\text{nn}}^{ij} D_{\text{n}}^{j} } \right){ = }p_{i} - \sigma_{\text{h}} \sin^{2} \theta_{i} - \sigma_{\text{H}} \cos^{2} \theta_{i} } } \hfill \\ \end{array} } \right.\left( {i,j = 1,2, \ldots ,N} \right),\,N = \sum\limits_{k = 1}^{M} {N_{k} }$$

(1)

The stress intensity factors (SIFs) at the HF tip can be easily determined by the displacement discontinuities of the fracture element (e.g., Olson and Taleghani 2009).

$$K_{\text{I}} = \frac{{GD_{\text{n}}^{\text{tip}} }}{2(1 - \nu )\sqrt r };\quad K_{\text{II}} = \frac{{GD_{\text{s}}^{\text{tip}} }}{2(1 - \nu )\sqrt r }$$

(2)

According to the maximum tensile stress criterion (e.g., Kim and Paulino 2007), the equivalent SIF of the I/II mixed mode fracture is

$$K_{\text{e}} = \frac{1}{2}\cos \frac{{\theta_{0} }}{2}\left[ {K_{\rm I} (1 + \cos \theta_{0} ) - 3K_{{^{\text{II}} }} \sin \theta_{0} } \right]$$

(3)

If $K_{\text{e}} > K_{\text{IC}}$, an HF initiates at an angle θ₀, which is measured anticlockwise from the HF to the new fracture tip.

$$\theta_{0} { = }\left\{ {\begin{array}{*{20}l} {0,} \hfill & {K_{\text{II}} = 0} \hfill \\ {2\arctan \left( {\frac{1}{4}\left( {\frac{{K_{\text{I}} }}{{K_{\text{II}} }} - \text{sgn} (K_{\text{II}} )\sqrt {\left( {\frac{{K_{\text{I}} }}{{K_{\text{II}} }}} \right)^{2} + 8} } \right)} \right),} \hfill & {K_{\text{II}} \ne 0} \hfill \\ {70.6^{ \circ } ,} \hfill & {K_{\text{I}} = 0} \hfill \\ \end{array} } \right.$$

(4)

The propagation step length of the fracture tip is given by

$$\Delta L^{\left( i \right)} = \left\{ {\begin{array}{*{20}l} {\frac{{K_{\text{e}}^{\left( i \right)} - K_{\text{IC}} }}{{\hbox{max} \{ K_{\text{e}}^{\left( i \right)} \} - K_{\text{IC}} }}\Delta L_{\hbox{max} } ,} \hfill & {K_{\text{e}}^{\left( i \right)} > K_{\text{IC}} } \hfill \\ {0,} \hfill & {K_{\text{e}}^{\left( i \right)} < K_{\text{IC}} } \hfill \\ \end{array} } \right.\quad i = 1,2, \ldots ,n$$

(5)

Fracturing fluid inside the fracture is assumed to be a power-law fluid. The flow equation (e.g., Cheng et al. 2017a) between two parallel plates is

$$\frac{\partial p}{\partial s} = 2^{n' + 1} \mu (\frac{1 + 2n'}{n'})^{n'} \frac{{Q^{n'} }}{{H^{n'} w^{2n' + 1} }}$$

(6)

Fluid conservation requires that the total injected fluid be equal to the sum of the leakoff volume into the porous rock and the fracture volume:

$$Q_{\text{T}} { = }\sum\limits_{k = 1}^{k = M} {\int_{0}^{{L_{k} \left( T \right)}} {wH} {\text{ds}}} { + }\sum\limits_{k = 1}^{k = M} {\int_{0}^{{L_{k} \left( T \right)}} {\int_{{t_{0} (s)}}^{T} {q_{\text{L}} \left( {s,t} \right){\text{d}}t} {\text{d}}s} } \quad \begin{array}{*{20}c} {} & {(i = 1,2, \ldots ,N_{M} )} \\ \end{array}$$

(7)

The Picard iteration method is adopted to solve the solid–fluid coupling problem during the dynamic propagation of multiple fractures. HF closure occurs after pump shutoff at the end of treatment. The proppant inside the HF retains its residual aperture. Nonlinear joint deformation is used to simulate the HF closure:

$$\sigma_{\text{n}} = - \frac{2}{\uppi }E_{\text{p}} \tan \left( {\frac{\uppi }{2}\frac{{\Delta D_{\text{n}} }}{{\left[ {D_{\text{n}} } \right]_{0} }}} \right),\begin{array}{*{20}c} {} & {} \\ \end{array} 0 \le - \Delta D_{\text{n}} < \left[ {D_{\text{n}} } \right]_{0}$$

(8)

The Newton–Raphson iteration method is adopted to solve for the nonlinear closure behavior after pump shutoff. The HFs in the subsequent stages must suffer the redistributed stresses induced by the previous fracturing stages.

$$\begin{aligned} & \left\{ {\begin{array}{*{20}l} {\sum\limits_{{j = S_{1} + S_{2} + \cdots + S_{k - 1} + 1}}^{{S_{1} + S_{2} + \cdots + S_{k} }} {\left( {{\mathbf{A}}_\text{ss}^{ij} \Delta D_{\text{s}}^{j} + {\mathbf{A}}_{\text{sn}}^{ij} \Delta D_{\text{n}}^{j} } \right)} = 0} \hfill \\ {\sum\limits_{{j = S_{1} + S_{2} + \cdots + S_{k - 1} + 1}}^{{S_{1} + S_{2} + \cdots + S_{k} }} {\left( {{\mathbf{A}}_\text{ns}^{ij} \Delta D_{\text{s}}^{j} + {\mathbf{A}}_{\text{nn}}^{ij} \Delta D_{\text{n}}^{j} } \right)} = - p_{i} - \frac{2}{\uppi}E_{\text{p}} \tan \left( {\frac{\uppi}{2}\frac{{\Delta D_{\text{n}}^{i} }}{{\left[ {D_{\text{n}}^{i} } \right]_{0} }}} \right)^{i} } \hfill \\ \end{array} } \right. \\ & \quad \left( {S_{1} + S_{2} + \cdots + S_{k - 1} + 1 \le i \le S_{1} + S_{2} + \cdots + S_{k} } \right) \\ \end{aligned}$$

(9)

With an increase in fracture closure, the new discontinuous displacement of the fracture element in stage k is

$$\left\{ \begin{aligned} \left[ {D_{\text{s}}^{j} } \right]_{\text{p}} = \left[ {D_{\text{s}}^{j} } \right]_{0} + \Delta D_{\text{s}}^{j} \hfill \\ \left[ {D_{\text{n}}^{j} } \right]_{\text{p}} = \left[ {D_{\text{n}}^{j} } \right]_{0} + \Delta D_{\text{n}}^{j} \hfill \\ \end{aligned} \right.\quad \quad \left( {S_{1} + S_{2} + \cdots + S_{k - 1} + 1 \le j \le S_{1} + S_{2} + \cdots + S_{k} } \right)$$

(10)

Normally, during the second step of TTSF, several days will have passed from the end of the first step; although the stress shadowing effect may become weaker, it is still present because of the proppant acting inside the hydraulic fractures. The stress shadowing at any point p during or after the fracturing process is

$$\left\{ {\begin{array}{*{20}l} {\Delta \sigma_{xx}^{p} = \sum\limits_{j = 1}^{N} {\left( {{\mathbf{B}}_{xx\text{s}}^{pj} D_{\text{s}}^{j} + {\mathbf{B}}_{xx\text{n}}^{pj} D_{\text{n}}^{j} } \right)} } \hfill \\ {\Delta \sigma_{yy}^{p} = \sum\limits_{j = 1}^{N} {\left( {{\mathbf{B}}_{yy\text{s}}^{pj} D_{\text{s}}^{j} + {\mathbf{B}}_{yy\text{n}}^{pj} D_{\text{n}}^{j} } \right)} } \hfill \\ {\Delta \sigma_{xy}^{p} = \sum\limits_{j = 1}^{N} {\left( {{\mathbf{B}}_{xy\text{s}}^{pj} D_{\text{s}}^{j} + {\mathbf{B}}_{xy\text{n}}^{pj} D_{\text{n}}^{j} } \right)} } \hfill \\ \end{array} } \right.$$

(11)

The redistributed stress field at any point p is given by the superposition of stress shadowing and the in situ stress.

$$\left\{ {\begin{array}{*{20}l} {\sigma_{xx}^{p} = \Delta \sigma_{xx}^{p} { + }\sigma_{\text{h}} { = }\sum\limits_{j = 1}^{N} {\left( {{\mathbf{B}}_{xx\text{s}}^{pj} D_{\text{s}}^{j} + {\mathbf{B}}_{xx\text{n}}^{pj} D_{\text{n}}^{j} } \right) + \sigma_{\text{h}} } } \hfill \\ {\sigma_{yy}^{p} = \Delta \sigma_{yy}^{p} { + }\sigma_{\text{H}} = \sum\limits_{j = 1}^{N} {\left( {{\mathbf{B}}_{yy\text{s}}^{pj} D_{\text{s}}^{j} + {\mathbf{B}}_{yy\text{n}}^{pj} D_{\text{n}}^{j} } \right) + \sigma_{\text{H}} } } \hfill \\ {\sigma_{xy}^{p} = \Delta \sigma_{xy}^{p} { + }0 = \sum\limits_{j = 1}^{N} {\left( {{\mathbf{B}}_{xy\text{s}}^{pj} D_{\text{s}}^{j} + {\mathbf{B}}_{xy\text{n}}^{pj} D_{\text{n}}^{j} } \right)} } \hfill \\ \end{array} } \right.$$

(12)

The principle stress and orientation of the redistributed stress field at any point p are

$$\left\{ {\begin{array}{*{20}l} {\sigma_{1} = \frac{{\sigma_{xx}^{p} + \sigma_{yy}^{p} }}{2} + \frac{1}{2}\sqrt {4\sigma_{xy}^{p2} + \left( {\sigma_{xx}^{p} - \sigma_{yy}^{p} } \right)^{2} } } \hfill \\ {\sigma_{2} = \frac{{\sigma_{xx}^{p} + \sigma_{yy}^{p} }}{2} - \frac{1}{2}\sqrt {4\sigma_{xy}^{p2} + \left( {\sigma_{xx}^{p} - \sigma_{yy}^{p} } \right)^{2} } } \hfill \\ {\alpha^{p} = \frac{1}{2}\arctan \left| {\frac{{2\sigma_{xy}^{p} }}{{\sigma_{xx}^{p} - \sigma_{yy}^{p} }}} \right|} \hfill \\ \end{array} } \right.$$

(13)