1 Introduction and background

Fluidized bed drying, granulation and coating are important processes in pharmaceutical industries for solid dose formulation. The main advantage of using fluidized beds is that they provide efficient heat and mass transfer and can mix and agglomerate excipients and active material ingredients to produce uniform blends of particles (Walker et al. 2009). In a granulation process, water or water-based binder solution is sprayed on the particle surface to increase adhesion forces so that agglomerating excipients can be formed. A drying process is the inverse process of granulation. During a drying process, water is extracted and other solvents are removed from particles to provide a sufficient shelf life. During a granulation, coating or drying process, particle properties including particle density, particle diameter, viscosity and restriction coefficient can change dramatically due to the change in moisture and agglomeration. All these parameters would affect the hydrodynamic behaviour in a fluidized bed process (Geldart 1973; Gidaspow et al. 1992).

Currently, the most serious problem in a fluidized bed process in pharmaceutical industry is the occurrence of undesired agglomeration with high moisture content and high temperature when the particles adhere to each other to form larger entities (Naelapaa et al. 2007). This undesired agglomerating is totally different from the desired process, which fixes the primary particles together so that larger porous secondary particles are formed (Palzer 2005). These entities can easily stick on to the hot wall which results in fault drying and defluidization. Furthermore, these entities are difficult to dry, resulting in a non-uniform product at the end of the process. The required moisture level, i.e. the end-point, cannot be reached, and the product quality cannot be guaranteed. For a granulation or coating process, some particles would be over-wet or over-drying. Therefore, it is necessary to consider new technology to monitor the processes not only for fault diagnosis, but also for controlling the fluidized bed conditions in the pharmaceutical industry or other industries using fluidized bed processes (Srinivasan and Qian 2006). In addition, the fundamental understanding of the fluidized bed coating and drying process is necessary for scaling up the fluidized bed reactor from a small scale to a production scale (Behzadi et al. 2008), reducing the risk from batch to continuous process design (McKenzie et al. 2006).

Up to now, there are several approaches that have been tried for the process monitor and moisture measurement in pharmaceutical fluidized bed dryer, e.g. capacitance probes (Davies and Talion 2004), near infra-red (Liu et al. 2017) and microwave resonance (Peters et al. 2018). However, most of them are not suitable for online fluidized bed monitoring (Che et al. 2018a) and do not fully comply with the regulations of Food and Drug Administration (FDA) (Gradinarsky et al. 2006). For the multi-phase flow process in a fluidized bed dryer, the non-intrusive imaging methodology provides a useful tool for process monitoring and fault diagnosis (Che et al. 2018b). Compared with other process tomography techniques and considering non-conductive material in the drying process, electrical capacitance tomography (ECT) is the most suitable imaging technique for measuring fluidized bed drying processes in pharmaceutical industry because it is fast and can reconstruct a permittivity distribution in a cross-sectional area (Yang and York 1999). The objective of this research is to investigate the behaviour of drying process in a fluidized bed by ECT with and without Wurster tube, which can provide online monitoring and fault diagnosis and possibly provide a new approach to process control.

To achieve the above objective, an ECT sensor with eight electrodes was designed and used to monitor the fluidized bed drying process with different operation conditions in a pharmaceutical fluidized bed dryer. Key process parameters including process moisture, cross-sectional solid concentration, time-averaged raw capacitance signals, averaged solids concentration in the chamber, the effect of Wurster tube on hydrodynamic behaviour and the dominant frequency spectrum distribution in the chamber were analysed. Test results indicate that process moisture change can be addressed from the raw capacitance of adjacent electrode pair combined with calibration model. Experimental results show that ECT technology can be used in pharmaceutical fluidized bed process monitor and control. Future work is given at the end of this paper.

2 ECT sensor design and image reconstruction

2.1 ECT data acquisition system and sensor design

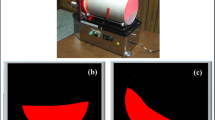
In this research, an ACECT is used to collect the capacitance data. The acquisition system consisted of a control box with 16 channels (Yang and York 1999). The excitation frequency can be programmed in the range of 10 kHz to 500 kHz, and voltage amplitude can be programmed in the range of 0 to 20 V. During measurement, one channel is as the excitation channel and all the other channels as detecting channels. The box is connected with PC through an NI DQACard-6024E. All the functions can be operated through a software interface as shown in Fig. 1a. Figure 1b, c gives the ECT sensor design and constructed in a fluidized bed dryer (Wang et al. 2010). The ECT sensor consisted of eight electrodes made up of adhesive copper tape stuck to a vinyl tiles sheet and stuck to the bowl using double-sided foam tape as shown in Fig. 1b. The core of the coaxial cable was soldered to the electrode. The shield of the cable was connected to the stainless wall of bowl, and the bowl was used as the earth. For an 8 electrode ECT sensor, there are 28 capacitances. In Fig. 1c, the fluidized bed dryer consists of a plenum in the bottom, a conical chamber with a height of 350 mm, an expansion chamber with a height of 500 mm and a filter on the top. The conical chamber and the expansion chamber are made of Plexiglas with thickness of 0.5 cm, which enable the visual observation of the particle flow. The bottom and top diameters of the conical chamber are 15 mm and 25 mm, respectively.

Fig. 1
figure 1

ECT software interface and sensor design

Full size image

2.2 ECT image reconstruction

Linear back-projection (LBP) is a simple image reconstruction algorithm and has commonly been used in ECT for 2D image reconstruction. For 2D images reconstruction, it is given by

$$G(x,y) = {{\sum\limits_{i = 1}^{N - 1} {\sum\limits_{j = i + 1}^{N} {C_{ij} S_{ij} (x,y)} } } \mathord{\left/ {\vphantom {{\sum\limits_{i = 1}^{N - 1} {\sum\limits_{j = i + 1}^{N} {C_{ij} S_{ij} (x,y)} } } {\sum\limits_{i = 1}^{N - 1} {\sum\limits_{j = i + 1}^{N} {S_{ij} (x,y)} } }}} \right. \kern-0pt} {\sum\limits_{i = 1}^{N - 1} {\sum\limits_{j = i + 1}^{N} {S_{ij} (x,y)} } }}$$
(1)

where G(x,y) is the grey level in a pixel (x,y), i.e. the reconstructed image, Cij is the normalized capacitance, Sij is sensitive map which in this case was obtained using FEM simulation software, and N is the number of electrodes. To obtain high-quality images, the Landweber iteration algorithm has been implemented (Yang et al. 1999) and is given by

$$G^{(n + 1)} = G^{(n)} + \alpha S^{\text{T}} \left( {C - SG^{(n)} } \right),\quad (n = 1,2,3, \ldots )$$
(2)

In this algorithm, the first image vector G(0) is reconstructed using Eq. (1). Each subsequent image vector G(k+1) is obtained from the previous image G(k) with an added correction term \(\alpha S^{\text{T}} (C - SG^{(k)} )\). In Eq. (2), \(C - SG^{(k)}\) is the error between the measured capacitance vector C and a re-calculated capacitance vector \(SG^{(k)}\). The error is used to reconstruct the next image. Figure 2 shows image reconstruction results for static test at three different positions in the chamber with two different paper tubes filled with pellets.

Fig. 2
figure 2

Image reconstruction for static test

Full size image

3 Experimental results

3.1 Drying process monitoring

Figure 3 shows the raw capacitance and process moisture change during a drying process with two different process conditions. To reduce the noise effect on the signals, low-pass filter was used to clearly indicate the capacitance change in the process. From these curves, the effect of flow rate and temperature on the drying process can be seen. The drying time can be dramatically changed from 45 min as shown in Fig. 3a to 24 min as shown in Fig. 3b. The change in raw capacitance from adjacent electrode pair gives the tendency of process moisture change. For all the above cases, the signals quickly decreased in the first few minutes and then tended to decrease slowly at the end of dying. The measurement results agreed well with the drying theory, i.e. there are two drying stages for fine particles. These two stages are constant drying and falling-on drying stage, respectively (Vojtech et al. 1996).

Fig. 3
figure 3

Raw capacitance data and moisture change in a drying process with different operation conditions

Full size image

Comparing Fig. 3a, b, it can be seen that the fluctuation of the original signal with the low flow rate is smaller than that with the high flow rate. This can be seen more clearly in terms of dominant frequency spectrum analysis as shown in Fig. 4. With low flow rate, the dominant frequency is around 4.3 Hz and 2.6 Hz for the middle flow rate. With high flow rate, there is no obvious dominant frequency. The above signals are taken at the beginning of drying with the same moisture level for the three cases. It should be noted that the dominant frequency is used to indicate the fluctuation of particle phase in the fluidized bed dryer process, and it is different from that used in the ECT data acquisition system for the signals excitation frequency. The excitation frequency is in the range of 10 kHz and 500 kHz, and the dominant frequency is in the range of 0 Hz and 10 Hz.

Fig. 4
figure 4

Domain frequency spectrum distribution with different flow rates

Full size image

Figure 5 compares the image reconstruction results and dominant frequency spectrum distribution in different drying times with two different flow rates. For the low flow rate and low drying temperature, the images show the change in particle permittivity distribution in moisture. The frequency changes from 4.5 Hz at the beginning to 8.5 Hz at the end of drying. This means that the flow behaviour changes from slow fluctuation to fast fluctuation due to the change in particle density with drying time. For the high flow rate and high drying temperature, the frequency changes from 2.8 Hz at the beginning to 3.9 Hz at the end of drying. Comparing those two drying conditions, the change in frequency is smaller than that with the low flow rate, which means the flow rate dominates the effect of flow behaviour in a fluidized bed dryer instead of the drying temperature.

Fig. 5
figure 5

Image reconstruction and dominant frequency spectrum distribution in different drying conditions

Full size image

Based on the drying curves as shown in Fig. 3, the drying rate can be calculated by

$${\text{Drying}}\;{\text{rate}} = \frac{{{\text{d}}X_{\text{p}} }}{{{\text{d}}t}} = \frac{{X_{\text{p}}^{i} - X_{\text{p}}^{i - 1} }}{{t^{i} - t^{i - 1} }}$$
(3)

where ti is the current time and ti−1 is the previous time in the drying process.

Figure 6 gives the drying rate calculated based on Eq. (3) with different drying conditions. The result indicates that with the increase in inlet temperature, the evaporating rate increases not only in the constant-rate periods, but also in the fall-rate periods. In the constant-rate period, the saturated pressure on the powder surface is the main evaporating force and its values depend on the drying air temperature and humidity. In the falling-rate periods, the evaporating rate inside the particle depends on the water vapour diffusion coefficient. The diffusion coefficient is a function of the particle temperature. The particle temperature depends on the heat flux from drying medium to it. For high inlet temperature (55 °C), the drying rate in the falling-rate period is faster than that with low inlet temperature (30 °C). In the first drying stage, high flow rate results in higher drying rate (Kunii and Levenspiel 1991). The reason is that the mass and transfer coefficient for high flow rate are bigger than those for the low flow rate. This indicates that at the first stage, it is better to use higher flow rate, and in the second stage it is better to use high drying temperature.

Fig. 6
figure 6

Drying process with different conditions

Full size image

Figure 7 shows the averaged solids concentration along the radial direction with different fluidization velocities. Figure 7a shows the value at the beginning of drying and Fig. 7b at the end of drying. Comparing the solids concentration in this figure, the profiles for the case of F = 35 m3/h and F = 45 m3/h have different distributions at the beginning and at the end of drying. The main reason is as follows. Due to high moisture content at the beginning, the pellets are very difficult to be fluidized with low flow rate, as shown in Fig. 7a, and therefore the solids concentration has high value both in the centre and near wall regions. However, due to low moisture content, the density of pellets reduced and it is easy to fluidize even with low flow rate at the end of dying. Therefore, the solids concentration has lower value than that at the beginning of drying. This is the main reason to keep an optimized fluidization flow rate during the drying process with different moisture contents (Wang et al. 2009).

Fig. 7
figure 7

Averaged solids concentration with different fluidization velocities (pellets weight 600 g)

Full size image

Figure 8 compares two batches of drying with different weights of pellets. For a high loading material process as shown in Fig. 8a, the solids concentration has different tendencies in the centre area and near wall area with drying time. However, the solids concentration has the same tendency both in the middle and near wall areas for low loading pellets. In terms of heat and mass transfer, there is an optimum solids distribution and total process weight for the special drying chamber. This will be kept for future work to optimize fluidized bed drying process.

Fig. 8
figure 8

Averaged solids concentration at different drying times

Full size image

3.2 Fluidized bed dryer with Wurster tube

In the following tests, two different lengths of Wurster tube were put inside in the fluidized bed chamber and atomizer air was used to blow the particle through dual-flow spray atomizer nozzle. The length of the Wurster tube is 8.6 cm and 4.5 cm, respectively. The gap between the bottom of the Wurster tube and the air distribution is 1.5 cm for all the tests.

Figures 9 and 10 give the image reconstruction results for Wurster fluidized bed with different operation conditions. For the long Wurster tube, there are more air bubbles in the chamber than that with the short Wurster tube. From the image, it is difficult to see the effect of atomizer air on the solid distribution in the chamber for both cases. The flow rate effect is also not obvious for both cases.

Fig. 9
figure 9

Image reconstruction for fluidized bed with long Wurster tube

Full size image
Fig. 10
figure 10

Image reconstruction for fluidized bed with short Wurster tube

Full size image

Figure 11 shows the process curves for a Wurster fluidized bed with different operation conditions. With long Wurster tube, the effect of atomizer air on average raw capacitance is clear, i.e. the data decrease with the increasing of atomizer air pressure. For short Wurster, the effect is not clear compared with the long Wurster tube. For both cases, the raw capacitance first increases with the increasing of flow rate (from 16 to 31 m3/h) and then decreases with the further increasing of flow rate (from 31 to 45 m3/h).

Fig. 11
figure 11

Process curves for fluidized bed drying with Wurster tube

Full size image

Figure 12 compares the image reconstruction results with and without Wurster tube and with the same process condition. It is clear that Wurster has effect on flow hydrodynamic in the chamber of the fluidized bed. However, it needs further validation to the ECT measurement results with more complex ECT sensor by putting ECT sensor both inside and outside of the Wurster tube. This will be kept for the future work for ECT test in a Wurster fluidized bed.

Fig. 12
figure 12

Image reconstruction for fluidized bed with and without Wurster tube

Full size image

Figure 13 shows the effect of total material weight on the process behaviour. With less material, the process signal decreases with the increasing of flow rate. With the increasing of process material, the measurement result gives the inverse tendency as depicted in Fig. 13b. This phenomenon can be easily explained by the fluidization process as demonstrated in the same figure. With the same fluidization flow rate, there are fewer particles in the same ECT sensors level with less loading material. With the increase in flow rate, more particles are blowing up to the top surface of the chamber. Therefore, the capacitance signal reduces with the increase in flow rate. Alternatively, for the more loading material case, more particles are blowing into the ECT sensor level area, and therefore the capacitance signal increases with the increase in flow rate. In addition, this phenomenon is related to the ECT sensor geometry size and physical properties, i.e. the sensor length along the chamber and the electrode sensitivity area. For accurate measurement and process control, optimum design for ECT sensor is necessary.

Fig. 13
figure 13

Effect of material weight on the process measurement

Full size image

Figure 14 shows the raw capacitance change in the spraying and drying process with Wurster tube fluidized bed and the image reconstruction results in time-sequence. The capacitance increases in the time period of 2 to 15 min and then deceases after the time periods of 15 min and 45 min in drying and the capacitance returns to the original value at the end of the drying at 46 min. In the time period of 46 min to 52 min, the process is in an extreme condition, i.e. over-spraying process. In this process, more and more water was sprayed into the fluidized bed and the pellets stuck together and stopped to fluidize. It also can be seen from the reconstructed images that the solid concentration increases first and then decreases until it recovers to the initial point at the end of drying. Due to more water spraying into the chamber, the pellets become over-wet and capacitance reaches to the upper limit of the ACECT system. The pellets start to fluidize again after 54 min without spraying water further.

Fig. 14
figure 14

Process curve for spraying and drying in one batch with Wurster tube and ECT images

Full size image

3.3 Predicating solids moisture content

Figure 15a gives the process moisture change with different operation conditions. The end-point of moisture contents varied in the range of 1.87% and 3.36% depending on the process flow rate and drying temperature. The drying time dramatically changes from 24 to 100 min. Figure 15b gives the averaged capacitance from adjacent electrode pair with different drying conditions. The end-point of measurement data changes from 252.5 to 264.4. The curves shown in Fig. 15b have the same tendency as the curves shown in Fig. 15a.

Fig. 15
figure 15

Moisture and capacitance curves versus time with different process conditions

Full size image

Figure 16 shows the process signals and gradient changes for the measurement signals. Figure 16a is a drying process with middle flow rate and inlet temperature and Fig. 16b with high flow rate and high inlet temperature. The fluctuation is strong at the beginning of drying and tends to become smooth at the end of drying for both cases. With high flow rate and inlet temperature, the fluctuation is stronger than that with middle level of flow rate and inlet temperature. It is possible to use the gradient changes to determine the end-point of drying in terms of control.

Fig. 16
figure 16

Process signals and gradient change

Full size image

Figure 17 shows the change in moisture content during one entire fluidized bed drying process based on the measurement capacitance signal and reference measurement. The detailed method for moisture measurement based on ECT sensor is given in reference (Wang et al. 2008). The reference moisture measurement is based on loss-of-weight (LOW) methods by an HB43 moisture metre from Mettler Toledo. For the above drying processes, the uncertainty of the measured moisture is 18% ± 4.3% at the beginning of a drying process and between 2% ± 0.5% at the end of the drying process. To achieve more accurate results, it is necessary to use more calibration data. In fact, the results from the moisture metre also depend on the sample material. More samples would result in more accurate results.

Fig. 17
figure 17

Moisture predicted by ECT sensor and moisture metre

Full size image

4 Conclusions

This research gives the preliminary ECT test results for drying process in a fluidized bed dryer with different operation conditions. Image reconstruction results show that ECT can track the change in solids moisture. Raw capacitance signals give the process information, i.e. process moisture level. However, further work is necessary to solve out the relationship between particle moisture, solids concentration and raw capacitance. Dominant frequency spectrum analysis is a useful tool to identify flow regimes and monitor process condition in the drying process. In addition, the effect of Wurster tube on the gas–solids flow characteristics is also investigated and the result demonstrates the flow characteristic changes. The above result indicates that ECT Imaging technology can be used in pharmaceutical fluidized bed drying process. For the application of ECT in drying process, efficient electrode construction is the key to the commercial success of this technology as applied to industrial fluidized beds. The adhesive used to stick the electrodes to the bowl wall is an important factor. Many adhesives loose their adhesion at higher temperatures. In addition, further work is necessary to optimize the electrode size and position in the chamber, as well as the frequency and amplitude required for the ACECT data readings.