1 Introduction

Following the successful application of multistage fracturing to shale gas reservoirs in the USA, the occurrence of a systematic method for unlocking the huge reserve of shale gas has been accepted across the world. Hydraulic fracturing often produces a complex fracture network in unconventional reservoirs (Yuan et al. 2015; Wang et al. 2017), as evidenced by microseismic monitoring (Fisher et al. 2002; Maxwell et al. 2002; Daniels et al. 2007). This aspect highlights the potential complexity of hydraulic fracture geometry, promotes the fracture conductivity near a horizontal well and finally enhances oil and gas production.

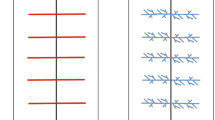
Huang and Kim (1993) conducted mine-back experiments, which show that a hydrofracture does not propagate linearly, but there are bi-wing fractures with several branches. The interaction between a hydraulic fracture (HF) and natural fracture (NF) can lead to the propagation of a fracture network (Jang et al. 2015; Cai et al. 2017), which is also influenced by heterogeneity of reservoir layers, irregular distribution of natural fractures and especially the in situ stress field (Olson 2008; Olson and Taleghani 2009). Weng et al. (2011) and Weng (2015) developed an unconventional fracture model (UFM) and considered stress field, the orientation of the NF and rock deformation, which is very powerful to describe the hydraulic fracture propagation using an unstructured grid. On the other hand, the wiremesh model (Xu et al. 2009, 2010; Meyer and Bazan 2011) utilizes two orthogonal sets of planar elements to represent the area of the fracture network and stimulated reservoir volume (SRV), which is simple but effective for network modeling (Weng et al. 2011). Fracture spacing, the complexity of the fracture network and the grid’s properties are considered during the hydraulic fracture propagation. The wiremesh model can incorporate many factors into the mathematical model because it uses planar network density to model the SRV rather than an individual fracture. Hence, both the UFM and the wiremesh model have advantages for representing the fracture network geometry and the influences on production. A performance-based simulation model has the following characteristics: (1) the main factors influencing the fracturing performance are connected to the fracture model. (2) The complexity of the fracture network geometry is recognized, and the intersection of HF and NF is modeled. (3) The area of the fracture model (or the SRV) is connected to the microseismic (MS) monitoring to better utilize the events of the MS. (4) The model does not represent the real situation in the reservoir but idealizes the fracture network based on the theories and assumptions.

In addition to the simulation approach, the connection of fractures influences the complexity of the network (Mayerhofer et al. 2006; Huang et al. 2014). Jones et al. (2013) and Chen et al. (2016) showed that the complexity and connectivity of the fracture network have great influences on production, implying that the bi-wing fracture model is not fit for the simulation of a complex fracture network. Otherwise, it is found that the critical zone of the stimulated volume is always smaller than the area obtained by the microseismic monitoring (Friedrich and Milliken 2013; Rahimi Zeynal et al. 2014). These problems motivate the development of a fracture model that is multileveled and easily adjusted. The fractal geometry theory was put forward by Mandelbrot (1979) and applied to rock mechanics since 1982 (Xie 1996). Microscale pore structure experiments show that the extension of a fracture is not irregular and can be expressed with different types of fractal theoretical models (Katz and Thompson 1985; Pande et al. 1987; Wei and Xia 2017). Fractal theory has been applied to characterize the heterogeneity of hydraulically fractured porous media in tight oil reservoirs (Wang et al. 2015a; Zhao et al. 2016). An iteratively determined tree-like fractal bifurcation has been introduced to study complex fracture network performance (Wang et al. 2015b), which is able to capture the details of multilevel bifurcated fractures in different orders and branches. The key formula that controls the tree-like fractal is the minimum entropy principle, which is also applicable to fracture description.

In this paper, a novel method for complex fracture network characterization is presented based on fractal geometry theory. The main parameters for the fractal fracture network are discussed to estimate its influence on the contributing reservoir volume (CRV). The combination of the commercial simulator and a field case study of CRV calibration and refracturing show the advantages of the fractal fracture model (FFM) for these applications.

2 Fractal fracture model

2.1 Integrating fractal geometry into fracture modeling

In order to describe the complex fracture network more precisely, we introduce a new fracture simulation model based on fractal geometry theory. The fractal geometry theory presented by Mandelbrot (1979) has been applied to rock mechanics since 1982 (Xie 1996). Iterated function system (IFS) and Lindenmayer system (L-system) are widely utilized to describe the growth of plants (Lindenmayer 1968; Han 2007). L-system is a rewriting system that defines a complex object by replacing parts of the initial object according to rewriting rules, which can simulate development rules and topological structure. The system has the feature of self-adjusting when something bifurcates, and this feature can describe the growth of trees well. In this paper, we introduce the L-system to characterize the fracture propagation pattern, due to the similar development rules and topology as the growth of trees. The interaction between HF and NF could be regarded as a type of rule-adjusting procession affecting the propagation of the fracture, which coincides with the basement of the L-system.

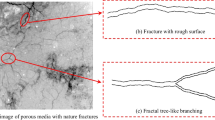
Figure 1 compared a typical crack obtained from mine-back experiments with the fracture geometry generated through the L-system method; it can be seen that either the main trunk or the overall pattern of two series shows high similarity. Moreover, the complexity of the actual fracture network will be much greater with the development of natural fractures in reservoirs, and the fractal fracture could also be developed for different requirements.

Fig. 1
figure 1

Comparison between cracks obtained from mine-back experiments and fractal fracture model [Fig. 1a is modified from Huang and Kim (1993); Fig. 1b, c is the fractal fracture geometry obtained by the L-system with respect to different iteration times]

Full size image

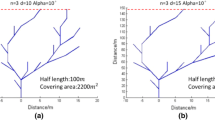
In the following discussion, the fractal fracture network is assumed to be the same at different stages, and the representative element unit is assumed to be a half-wing of HF. By adjusting the parameters of the fractal fracture model, the geometry of a fracture network can be generated for performance evaluation and matching the MS monitoring events by multiple parameters, such as fracture half-length, SRV, fracture density and intensity of the events (associated with the complexity and the effectiveness of the fracture network) (Fig. 2).

Fig. 2
figure 2

Schematic of the representative element unit [the overall schematic of fracture is modified from Stalgorova and Mattar (2012); blue lines show the fractal fracture geometry generated by the L-system]

Full size image

2.2 Control factor

Zhou et al. (2016) defined four key parameters to control the generation of fractal fractures, and these parameters directly affect the length of fractal fractures, size and “complexity” of fracture geometries. (1) The generating length (d) depends on the length of the main fracture and its branches: the parameter controls the length of each fracture segment, so when d increases, the area of the fracture network expands. (2) The deviation angle (α) controls the orientation when the fracture deviates or generates a secondary branch; the parameter can be adjusted according to the orientation of the stress field and connects highly with the covering area of the fracture network. (3) The iteration time (n) controls the extension of the fractal fracture according to the growth of the fractal tree. It influences the complexity of the generated fracture network and should be adjusted to match the density of microseismic events (MSE). For example, in Fig. 1b the fractal fracture iteration is twice, and in Fig. 1c iteration is three times. (4) The generating rules control the growth of the bifurcation. Incorporating with the iteration times, the fractal fracture model could fit numerous fracture geometries under different geological and engineering situations.

3 Model validation

The fracture network geometry is generated and discretized into 2D grids to represent the conductive fracture that contributes to the production. In this paper, we use the E300 simulator for numerical simulation, the keyword CONDFRAC is utilized by assigning the value of the properties to each fracture. The main properties of the fracture relevant to the production are the aperture and permeability which influence the conductivity of the fracture network. Data for the simulation model are obtained and simplified from a shale gas reservoir in China. The values are listed in Table 1. The workflow for fractal fracture simulation is shown in Fig. 3. We first generate the complex fractal fracture network using the L-system and then output the coordination of fractures as the microseismic events. After scaling up the MSE, we can assign the fracture properties into each grid. With the help of reservoir simulation and microseismic events, the multilevel fracture network geometry can be converted to the fracture network with properties contributing to the production.

Table 1 Synthetic data used for fractal fracture simulation
Full size table
Fig. 3
figure 3

Schematic workflow for fractal fracture simulation

Full size image

To valid the fractal fracture model with the production data gathered from field cases, the geometry was generated by matching the fairway length and fairway width in the SRV. Fractal fracture conductivity should be expected to decrease in time due to partial fracture closure. The first- and second-level fractures are assigned with a conductivity of 4.2 mD m, and the third-level fractures are assigned a value of 0.6 mD m for better production matching. It should be noted in Fig. 4 that the shale gas production trend was closely matched by the fractal fracture model.

Fig. 4
figure 4

History matching with a field case using the fractal fracture model

Full size image

4 CRV calibration and refracturing simulation

4.1 CRV calibration

In the field study, a fractured horizontal well sometimes does not perform well although the SRV monitored by microseismic events shows that a mass of fracture networks is generated (Huang et al. 2016). According to the reservoir simulation, the well performance should be higher if the overall stimulated reservoir area is regarded as being filled with a high conductivity fracture network, so the real contribution of the networks is overestimated. Rahimi Zeynal et al. (2014) proposed that the contributing stimulated volume is relatively smaller than that of the microseismic monitored through rate-transient analysis. The effective proppant volume (EPV) is different from the SRV (Friedrich and Milliken 2013). EPV represents the volume filled with proppant, and it covers the main fracture network stimulated with higher conductivity and contributes most to the production.

Theoretically, with multilevel features of fractal fractures, EPV estimation can be carried out by adjusting the properties with respect to different levels of fractures. Figure 5a shows when the iteration increases, there will be more reservoir area covered by fractal fracture networks, but except for the difference, the main fracture networks (CRV) have higher conductivity and the outer region as the transition zone has a lower conductivity. Figure 5b compares results of cumulative production; the result shows that main fracture network contributes over 80% (nearly 85% on average) of the total production. The induced fractures (outer fracture network) developed by the intersection of natural fractures and hydraulic fractures provide the other 20%. On the other hand, the cumulative production curve increases as time goes on, implying that the early production is mostly provided by the main fracture, but the final production is related to the area of the outer connected networks. Here, the main fracture can be regarded as the effective proppant area which has higher conductivity, and the outer region as the transition zone which is not effectively filled with proppant. Even when monitored by microseismic there are massive signals in this transition zone, it does not mean that the fractures here have a great contribution to production. So far we have estimated the actual half-length of the main fracture is approximately 80 m, which may smaller than the monitoring fairway length.

Fig. 5
figure 5

The comparison of different features of the fracture network

Full size image

4.2 Simulation of refracturing

Many reasons cause the fractured horizontal well production to decrease, such as completion suffered damage, drilling mud loss, fines migration and fracture plugging. For such kind of wells, refracturing can reopen the existing perforations and fracture network to revitalize the productivity (Elbel and Mack 1993). In the case of formation damage, it can reopen the existing fracture networks and restore the fracture conductivity to the wellbore, which is known as “reconnect” treatment strategy.

As we know, either increasing the network complexity, fracture conductivity or extension of SRV would be the desired results of refracturing design. However, the performance of refracturing is highly dependent on the geological and engineering conditions, so selecting economic refracturing candidates presents a key problem (Reese et al. 1994). The fracture geometry can be specified in the self-independent adjustment feature of FFM, which yields a convenient method for pre-designing and simulating the refracturing performance and selecting the refracturing candidates economically. For simulating refracturing performance, five cases were considered. Figure 6 presents the fracture geometry of a half-wing for the different cases; the dashed lines in red show the change of the fracture resulting from refracturing.

Fig. 6
figure 6

Fractal fracture geometry for refracturing simulation (primary fracture in solid lines; new fractures or fracture network generated by refracturing in dashed lines)

Full size image

  • Case 1 The original fractal fracture network and stimulated reservoir volume, Fig. 6a;

  • Case 2 Part of the fracture network extended with the enhancement of fracture conductivity (SRV grows), Fig. 6b;

  • Case 3 The complexity of the total fracture network and the area of SRV are both improved, Fig. 6c;

  • Case 4 The conductivity of part fracture network enhanced and fracture near the well extended (SRV does not grow), Fig. 6a;

  • Case 5 Both the complexity of the fracture network and the conductivity of the fracture are improved, Fig. 6d.

The improvement in the fracture network can be evaluated by monitoring or through fracturing engineering plans. By adjusting the properties of the fracture network in the simulation model, the cases are simulated and the results show as follows in Fig. 7. (1) Only enhancing the conductivity of the fracture network near the well without extending the area of SRV contributes less to the production. (2) The decline rate could be reduced when the area of SRV increases, but the contraction and the complexity (mainly controlled by the bifurcation times n in FFM) of the fracture network contribute most to the final cumulative production. (3) The final production rate is not controlled by the fracture properties but is determined by the boundary or the area of SRV, which follows the theory of DCA or RTA.

Fig. 7
figure 7

The production rate and total production simulated by different cases

Full size image

5 Conclusions

In this paper, we proposed a new type of fracture model based on fractal geometry theory to study and simulate the fracture network generated by hydraulic fracturing. The model has advantages compared to the wiremesh and UFM approaches in that the geometry of the fracture network is related to several fractal parameters that can be adjusted with an understanding of geologic and engineering factors, as well as microseismic monitoring events. It is a type of performance-based model for characterizing the hydraulic fracture network. With FFM, both the propagation of the fracture network and the fractal controlling parameters can be specified and adjusted.

Simulation of the performance of refracturing and calibration of the CRV are two applications of FFM on fracture modeling based on features of the fractal fracture.

  • For refracturing, the model performs well for (1) designing the added branches or enhancing the fracture conductivity and (2) simulating the different cases resulted from the refracturing. The simulation results show that extending the area of fracture network is better than enhancing the conductivity of fractures for improving production.

  • Based on the multilevel feature of a fractal fracture, FFM provides a convenient and effective method to calibrate the CRV in a monitoring area, demarcating the main fracture or fracture network for understanding the performance of hydraulic fracturing, including the monitoring events and the production. The results suggest that the contributing area is smaller than that monitored and provides the early production, but the final cumulative production depends more on the area of SRV.

In addition to simulating the fracture network, the FFM presents advantages for further research between the fractal parameters, the fracture geometry and the production-related properties of fractures.