1 Introduction

Rock fractures are important oil storages and transport channels. The physical properties of fractures, along with the fractures’ development degree, are vital indices for evaluating reservoirs. Therefore, fractured rock’s acoustic and electrical parameters have become a focus for geophysicists and reservoir engineers. Many types of methods have been used to evaluate fractures in seismic exploration (Li 1997; Zhao et al. 2014; Kong et al. 2012). Among these, the compressional wave anisotropy (Liu et al. 2012; Ass’ad et al. 1992) and shear wave splitting (Baird et al. 2015; de Figueiredo et al. 2013; Guéguen and Sarout 2012) are the most widely used methods at the present time to evaluate fractures. The anisotropy and fracture parameters were obtained by seismic prospecting. However, the relationships between anisotropy and fractures are complex and required further technical development. The qualitative identification of fractures through conventional logs also had certain developments (Sun et al. 2014; Deng et al. 2009; Wang 2013). However, using conventional logs affected by many factors, as well as the limitations in vertical resolution, has led to difficulties in obtaining accurate identification of fractures. With the development of computer technology, along with advancements in well logging technology, imaging logs, like Formation MicroScanner Image (FMI), had now become an accurate basis for fracture identification (Qiao et al. 2005). However, because of high costs and the large amount of data, it was difficult to use the imaging logs on an entire well and in all wells (Aldenize et al. 2015). In addition, laboratory fracture simulation experiments have been widely performed. Due to fractures, the collected core samples from boreholes broke easily, so that people cannot assess the actual situation underground, thus it is difficult to measure the fracture width of cores in the laboratory. Therefore, in the laboratory, the simulation method was used for the measurement of fractures in ultrasonic experiments (Faranak 2012). The physical simulation typically used a single material to simulate the rock, constructing through artificial means the pores and fractures to perform the measurement of the acoustic wave velocity, quality factor and other physical quantities with different fracture parameters (He et al. 2001; Li et al. 2016; Amalokwu et al. 2014; Wang et al. 2013). However, the single material simulation experiment had neglected the complexity of the mineral and pore distribution of the rock, so that the method was still faced with many problems in actual application. In addition, due to the fact that the acoustic wave attenuation was much more complicated than the change of the acoustic wave velocity, it was difficult to explain the principles of the acoustic wave attenuation using the physical model (Morris et al. 1964; Jose et al. 2013), thus most of the methods of acoustic wave amplitude were derived by means of numerical simulation, but the boundary conditions were too simple to match many problems in actual applications (Shi et al. 2004; Chen et al. 2012; Wang et al. 2015; Shragge et al. 2015).

It had been determined that the compressional and shear wave velocities will change when a large number of rock fractures exist (Quirein et al. 2015; Carcione et al. 2013). Fractures led the velocities to become abnormal. The relationship between the fracture width and the acoustic parameters obtained in the laboratory was the key to estimating fracture width. It has been found to be more accurate to obtain the compressional and shear wave velocities, as well as the acoustic wave amplitude, from the dipole shear wave logging (DSI) and array acoustic logging data (Xu et al. 2014; Chen and Tang 2012). Using the inversion of DSI and array acoustic logging data to evaluate the fracture width, the application of this method for the identification of fractures had very broad prospects and feasibility (Wang et al. 2012).

This study was different from the physical experiments of simulating fractures with a single material (Wei and Di 2007; Cao et al. 2004). Actual core samples were used to simulate the fractured rocks. An ultrasonic experiment was used to examine the acoustic parameters of the fractured rocks. The effects of the pores of the rock itself on the acoustic waves were eliminated. This point was found to be more accurate than ignoring the rock porosity. The influences of different fracture width on the acoustic wave velocity and amplitude were studied. Two variables were defined: H represents the amplitude attenuation ratio of the compressional and shear wave, and x represents the transit time difference of shear wave and compressional wave divided by the transit time of the compressional wave. Transit time is the slowness of the acoustic wave. The effects of fracture width on the two physical quantities, H and x, were analyzed. The method of quantitative evaluation of fractures was achieved by using H and x. This theory provided a new method for the quantitative calculations of fracture width, as well as the evaluation of fractures in laboratory settings. This method has been applied to actual well logging data and has obtained good results. It also provided a basis for fractured reservoir evaluation, which can be of assistance in the exploration and development of oil fields in the future.

2 Experimental devices and measurement methods

2.1 Preparation of samples and fractures

In this study, sandstone samples were cut across to simulate fractured rocks. Table 1 displayed the parameters of the core samples. The No. 1 and No. 2 samples were cut to simulate fractured rocks.

Table 1 Parameters of the core samples
Full size table

Due to the evaporation of moisture, it was difficult to maintain a unified state during the measurement of the acoustic wave velocity in a fully saturated condition. The cores were kept dry during the measurement process, in order to facilitate the comparison of the velocity change.

PET film was used to simulate the width of the fracture. The PET film was formed into an annulus, with an outer diameter of 24 mm, inner diameter of 20 mm and thickness of 0.06 mm. The number of the PET film annuli was used to control the width of fracture.

2.2 Method of measurement

The instrument used to conduct the experiment was an HF-F Intelligent Ultrasonic Tester (Fig. 1a). A KDQS-II Full Diameter Acoustic Analyzer (Fig. 1b) was the core holder and used to measure the acoustic wave. The pass bandwidth of the instrument was set at 0.1 to 1000 kHz. The instrument launched the electrical signal, and the transmitter probe transformed the signal into vibration. Then the receiver probe converted the vibration into electrical voltage. The unit of amplitude was V, representing voltage. The compressional and shear wave voltage transmitted by the instrument was 250 V. Triggered by the computer, the recording time length was 812.5 μs, the sampling interval was 0.0625 μs, and the waveform length of each record was 13,000 points. The acoustic wavelength launched by the acoustic instruments was much less than the fracture width. The measurements were taken at normal temperature and pressure. Wave propagation was along the vertical axis of the rock. During the measurements, a good coupling between the transducer and the rock was always maintained, and the transmitting and receiving transducer were located at the ends of the center axis. There was a single horizontal fracture in rock sample No. 1, and two parallel horizontal fractures in the rock sample No. 2 (Fig. 1c).

Fig. 1
figure 1

Experimental instruments and rock samples. HF-F Intelligent Ultrasonic Tester (a), KDQS-II Full Diameter Acoustic Analyzer (b), two rock samples (c)

Full size image

3 Repetitive experiment

The effects of accidental factors on acoustic propagation can be eliminated through repeated experiments. Due to the influence of different fracture width on the acoustic wave velocity and amplitude, the fracture width (W f) was made at 0.18 mm with layers of PET film. The experiment was repeated three times, measuring the compressional and shear wave velocity (V p, V s) and amplitude (A p, A s) of the No. 1 samples. The test results are shown in Table 2.

Table 2 Acoustic wave measurement of sample No. 1’s repeatability of the W f = 0.18 mm
Full size table

As can be seen from Table 2, the four parameters of sample No.1 from three repeated measurements were very similar and the relative standard deviation values were relatively small. It was safe to conclude that the results were stable and repeatable, which provided a reliable basis for our subsequent data analysis.

4 Results and analysis

4.1 Velocity measurement and analysis of core with a single fracture

The influence of fracture width on the acoustic wave velocity was investigated. Figure 2 showed rock’s variation of compressional wave velocity with the widths of the fracture of sample No. 1. The widths of the fractures were from 0 to 7 units, 0, 0.06, 0.12, 0.18, 0.24, 0.30, 0.36 and 0.42 mm. The thickness of each unit represented a layer of PET film.

Fig. 2
figure 2

Relationship between fracture widths and acoustic wave velocity of No. 1 rock. The filled circles and squares, respectively, represented the compressional and shear wave velocity of the core with the fracture. The fracture widths W f in the core were 0; 0.06; 0.12; 0.18; 0.24; 0.3; 0.36 and 0.42 mm

Full size image

When the fracture width was less than 0.42 mm, the variation of the V p along with the fracture widths was obtained by fitting the measured data as follows.

$$V_{\text{p}} = - 1509.8 \times W_{\text{f}} + 2797.6$$
(1)

The variation of the V s along with the fracture was as follows.

$$V_{\text{s}} = - 399.48 \times W_{\text{f}} + 1597.3$$
(2)

The above results showed that there were obvious relationships between the acoustic wave velocity and the development degrees of fractures in the rock.

The existence of fractures led to velocity decrease for both the compressional and shear waves. With the increases of the fracture width, the velocity continued to decrease and displayed a linear relationship when the fracture width was less than 0.42 mm. From the slope of the fitting line, it could be seen that the changes of shear wave velocity were smaller than those of the compressional wave. Thus, the existence of fractures and fracture width were the influence factors of the compressional and shear wave velocity.

The measured values obtained in the acoustic logging were the acoustic transit time. Therefore, the relationships between the velocity of the acoustic wave and the width of the fractures could be converted into the relationships between the acoustic transit time and the fracture width. In this study, in order to eliminate the influence of the rock’s porosity on the acoustic transit time and make the changes of the compressional and shear wave transit time only related to the fracture width, x was defined as follows:

$$x = {{\left( {DT_{\text{s}} - DT_{\text{p}} } \right)} \mathord{\left/ {\vphantom {{\left( {DT_{\text{s}} - DT_{\text{p}} } \right)} {DT_{\text{p}} }}} \right. \kern-0pt} {DT_{\text{p}} }}$$
(3)

where DT s is the transit time of the shear wave, s/m, which was 1/V s; and DT p is the transit time of the compressional wave, s/m, which was 1/V p.

The relationship between the fracture width and x of sample No. 1 is illustrated in Fig. 3.

Fig. 3
figure 3

Relationship between the fracture width and x

Full size image

In accordance with the data shown in Fig. 3, the formula for calculating the fracture width, W f, mm, was determined as follows:

$$W_{\text{f}} = - 1.6393x + 1.253$$
(4)

4.2 Velocity analysis of rocks with multiple fractures

In actual reservoirs, there are multiple fractures, rather than a single fracture. The impact of two parallel fractures on acoustic wave velocity was measured, and the acoustic wave velocities with the same width as a single fracture were compared. In dry conditions, between one and three PET films were placed in the two fractures of core sample No. 2, in order to simulate two parallel fractures with widths of 0.06, 0.12 and 0.18 mm. The relationships between the compressional wave velocity and the two parallel fracture widths were examined, and a comparison with the single fracture sample which had the same fracture width was performed. The results are shown in Fig. 4.

Fig. 4
figure 4

Velocity contrasts of the single and two parallel fractures. The filled circles and squares, respectively, represent the single and twin fractures compressional wave velocities of the core with the fracture. The single fracture widths in the core were W f = 0; 0.06; 0.12; 0.18; 0.24; 0.3 and 0.36 mm. The two fracture widths in the core were W f = 0; 0.12; 0.24; 0.30 and 0.36 mm

Full size image

Figure 4 shows that multiple fractures caused the compressional wave velocity to be approximately linearly reduced. Furthermore, when the fracture width was less than 0.36 mm, two parallel fractures had almost the same influence on the compressional wave velocity as the single fracture.

4.3 Analysis of the relationship between the amplitude attenuation and fracture width

The fracture widths of core sample No. 1 were 0, 0.06, 0.12, 0.18, 0.24, 0.30 and 0.36 mm. In order to compare the attenuation of the acoustic wave amplitudes, the amplitude of the compressional and shear waves was corrected to the same gain value using Eq. (5):

$$A_{2} = A_{1} \times {\text{e}}^{{0.1085 \times \left( {y_{2} - y_{1} } \right)}}$$
(5)

where y 1 was the gain before the correction; y 2 was the goal gain; A 1 was the amplitude before the correction, and A 2 was the amplitude after the correction. The amplitude after the correction was shown in Fig. 5.

Fig. 5
figure 5

Relationship between the fractures width and the amplitude of the acoustic wave. The filled circle and square represent the compressional and shear wave amplitudes of the core with the fracture. The fracture widths in the core were = 0; 0.06; 0.12; 0.18; 0.24; 0.3 and 0.36 mm

Full size image

The variation of the compressional wave amplitude, A p, with the changes of the fracture width was obtained by fitting the measured data as follows:

$$A_{\text{p}} = 2.0663 \times {\text{e}}^{{ - 3.5W_{\text{f}} }}$$
(6)

The variation of shear wave amplitude, A s, with the changes of the fracture widths was obtained by fitting the measured data as follows:

$$A_{\text{s}} = 1.1407 \times {\text{e}}^{{ - 1.288W_{\text{f}} }}$$
(7)

With the increases of the fracture width, the amplitudes of the shear and compressional wave were exponentially reduced. A pmax was the maximum amplitude of the compressional wave without fractures; and A smax was the maximum amplitude of the shear wave without fractures. A max − A was defined as the difference between acoustic wave amplitude without fracture and that with fractures. The relationship between A max − A and the fracture width is shown in Fig. 6.

Fig. 6
figure 6

Relationship between fracture width and acoustic wave amplitude attenuation. The filled squares and circles represent the A pmax − A p and A smax − A s. The fracture widths in the core were W f = 0; 0.06; 0.12; 0.18; 0.24; 0.3 and 0.36 mm

Full size image

From Fig. 6, it can be seen that, when there were fractures, the attenuation of the compressional wave was faster than that of the shear wave. The difference between A pmax − A p and A smax − A s increased gradually with the increase of fracture width. The ratio between the attenuation of compressional wave and the attenuation of shear wave was defined as H, in order to study the effect of fracture width.

$$H = {{(A_{{\hbox{pmax} }} - A_{\text{p}} )} \mathord{\left/ {\vphantom {{(A_{{\hbox{pmax} }} - A_{\text{p}} )} {(A_{{\hbox{smax} }} - A_{\text{s}} )}}} \right. \kern-0pt} {(A_{{\hbox{smax} }} - A_{\text{s}} )}}$$
(8)

Figure 7 illustrates the relationship between H and the fracture width.

Fig. 7
figure 7

Relationship between H and the fracture width

Full size image

When the fracture width was less than 0.36 mm, the relationship between H and fracture width, W f, was obtained by fitting the measured data as follows:

$$H = - 12.49 + 14.43{\text{e}}^{{ - W_{\text{f}} }} + 22.59W_{\text{f}} \times {\text{e}}^{{ - W_{\text{f}} }}$$
(9)

Equation (9) shows that when the fracture width was less than 0.36 mm, the greater the fracture width was, the greater the H was, and the H tended to be stable. The relationship was summarized, and the empirical value of H was used to evaluate the fracture width. The experiment showed that when H was greater than 2, there was a fracture.

5 Application examples of identifying fractures based on acoustic logging data

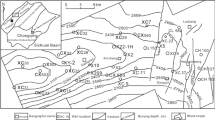
In order to verify the accuracy of Eq. (4), the DSI data of a well were calculated to evaluate the fractures. The depths from 2780 m to 2810 m and from 3008 m to 3060 m were two sections in which fractures were developed (Fig. 8). Since electrical imaging logging was a good method for identifying fractures, imaging log data were used to validate the results.

Fig. 8
figure 8

Sections logging data at 2780 to 2800 m and 3010 to 3060 m in well A

Full size image

In Fig. 8, the first track represents depth. The second track is the transit time of the compressional wave and shear wave, which were extracted from the DSI log data. The third track is the width of fractures by Eq. (4), obtained by calculating x according to the transit time. The fourth is the electrical imaging of FMI. The following four tracks show the fracture characteristics calculated from FMI, which were used to compare the calculation results of the fracture width.

The fracture-developed sections were located at 2784 to 2799 m (I), 3010 to 3015 m (II), 3033 to 3037 m (III) and 3051 to 3054 m (IV). Figure 8 illustrated that the calculated results through Eqs. (3) and (4) were coincident to the fractures of FMI.

Figure 9 illustrates the comparison of the H and FMI data of well B. The second track is the acoustic wave amplitude, and the third track is the acoustic wave attenuation. The fourth track represents H. The sixth is the static image and the fracture tracing. The seventh shows the tadpole plot of the fracture dip according to the imaging log, GR, and caliper curve. The last track is the dynamic image.

Fig. 9
figure 9

Comparison of the amplitudes and imaging results at 2570 to 2576 m and 2616 to 2623 m

Full size image

The pink area in Fig. 9 is the calculated H. It can be seen that the ratio was greater than 2 when the fracture developed. The results of the fracture evaluations were coincident to the fractures of FMI, which were in accordance with H. Due to the fact that the acoustic wave amplitude was sensitive to the response of the fracture, in the section of the fracture developed, the amplitude was attenuated. Therefore, when using the acoustic wave velocity to calculate the fracture, the resolution of the acoustic wave amplitude was higher. The exact calculation of fracture width from H remains to be studied.

6 Conclusions

  1. 1.

    The existence of fractures led to decrease of the acoustic wave velocity. The shear and compressional wave velocities were found to linearly decrease with the increases of the fracture width. The decrease of the compressional wave velocity was faster than the shear wave. The velocity of the acoustic wave was converted to the transit time. The ratios of the transit time of compressional wave and shear wave (x) were affected by fracture width, when the fracture width was less than 0.42 mm. With the increase of fracture width, x was becoming smaller and smaller. Fracture width can be calculated through the relationship between x and the fracture width.

  2. 2.

    The existence of fractures led to a decrease of the amplitudes of the compressional and shear wave. With the increase of the fracture width, the amplitudes of the compressional and shear wave decreased exponentially. The amplitude attenuation ratio (H) was defined, when there was a fracture, the H value was greater than 2. When the fracture width was less than 0.36 mm, the empirical value of H was gradually increased. According to this experience, the position of fractures in the reservoir can be located.

  3. 3.

    By measuring the effects of both the single and two parallel fractures on the compressional wave velocity, it was determined that when the width of the parallel fractures was equal to that of a single fracture, they had the same effect on the compressional wave velocity. This result was only applicable to the compressional wave, because the compressional wave velocity was less affected by the number of fractures.

  4. 4.

    Through experimental measurements, the method for evaluating fractures in the borehole by using x and H also was achieved. This study used wells A and B as application examples. The calculation results were compared with FMI data, with good agreement. The results verified that the rock acoustic parameters were affected by fractures in the borehole and provided a new method for the quantitative evaluation of fractures. In actual production, because of the influence of the fracture dip and fracture filler, this conclusion may exhibit a certain deviation, thus it will be studied by the authors in the future.

  5. 5.

    The next step will be to study the fracture of carbonate reservoirs and shale reservoirs.