A theoretical model linking interspecific variation in density dependence to species abundances

Abstract

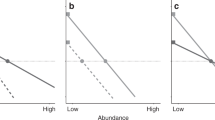
Understanding the factors that govern the commonness and rarity of individual species is a central challenge in community ecology. Empirical studies have often found that abundance is related to traits associated with competitive ability and suitability to the local environment and, more recently, also to negative conspecific density dependence. Here, we construct a theoretical framework to show how a species’ abundance is, in general, expected to be dependent on its per-capita growth rate when rare and the rate at which its growth rate declines with increasing abundance (strength of stabilization). We argue that per-capita growth rate when rare can be interpreted as competitive ability and that strength of stabilization largely reflects negative conspecific inhibition. We then analyze a simple spatially implicit model in which each species is defined by three parameters that affect its juvenile survival: its generalized competitive effect on others, its generalized response to competition, and an additional negative effect on conspecifics. This model facilitates the stable coexistence of an arbitrarily large number of species and qualitatively reproduces empirical relationships between abundance, competitive ability, and negative conspecific density dependence. Our results provide theoretical support for the combined roles of competitive ability and negative density dependence in the determination of species abundances in real ecosystems, and suggest new avenues of research for understanding abundance in models and in real communities.

Appendices

Appendix I: Coexistence in the absence of negative density dependence

We investigate coexistence in our model in the absence of negative density dependence (i.e., η _i  = 0). In this case, the master equation becomes:

$$ {p_{{i,t + 1}}} = \left( {1 - m} \right){p_{{i,t}}} + m{p_{{i,t}}}{\beta_i}g\left( {{\bf p}} \right) $$

It can be seen from this equation that β _i represents intrinsic fitness because it measures differences in relative growth rates in the absence of stabilizing forces (Chesson 2000). To solve for equilibrium, we let ${p_{{i,t + 1}}} = {p_{{i,t}}} = {\overline p_i}$. Assuming that ${\overline p_i} \ne 0$, we have:

$$ {\beta_i}g\left( {{\bf p}} \right) = 1 $$

$$ {\beta_i}\mathop{\sum }\limits_j \frac{{{p_{{j,t}}}}}{{f\left( {{\bf p}} \right)}} = 1 $$

$$ {\beta_i} = \mathop{\sum }\limits_j {\beta_k}{p_k} $$

which means that every species that persists at equilibrium must have an identical value of β _i . The master equation then degenerates to:

$$ {p_{{i,t + 1}}} = {p_{{i,t}}} $$

meaning that species will persist at their initial abundances. This model is clearly only neutrally stable.

Appendix II: Mathematical details from equilibrium abundances section

We want to show that $g\left( {\overline {{\bf p}} } \right)$ declines monotonically with the addition of more (stably coexisting) species to the system defined by (2). Start with a system of n (stably coexisting) species with equilibrium relative abundances ${\overline {{\bf p}}_n}$, so that:

$$ g\left( {{{\overline {{\bf p}} }_n}} \right) = \frac{{\sum_{{i = 1}}^n\frac{1}{{{\beta_i}{\eta_i}}}}}{{\left( {\sum_{{i = 1}}^n\frac{1}{{{\eta_i}}}} \right) - 1}} $$

Now add another (stably coexisting) species to the system so that there are n + 1 species and:

$$ g\left( {{{\overline {{\bf p}} }_{{n + 1}}}} \right) = \frac{{\frac{1}{{{\beta_{{n + 1}}}{\eta_{{n + 1}}}}} + \sum_{{i = 1}}^n\frac{1}{{{\beta_i}{\eta_i}}}}}{{\frac{1}{{{\eta_{{n + 1}}}}} + \left( {\sum_{{i = 1}}^n\frac{1}{{{\eta_i}}}} \right) - 1}} $$

We know from the coexistence condition (4) that:

$$ {\beta_{{n + 1}}} > \frac{{\left( {\sum_{{i = 1}}^n\frac{1}{{{\eta_i}}}} \right) - 1}}{{\sum_{{i = 1}}^n\frac{1}{{{\beta_i}{\eta_i}}}}}. $$

This in turn implies that:

$$ \frac{1}{{{\beta_{{n + 1}}}}} < \frac{{\sum_{{i = 1}}^n\frac{1}{{{\beta_i}{\eta_i}}}}}{{\left( {\sum_{{i = 1}}^n\frac{1}{{{\eta_i}}}} \right) - 1}} = g\left( {{{\overline {{\bf p}} }_n}} \right) $$

and thus:

$$ g\left( {{{\overline {{\bf p}} }_{{n + 1}}}} \right) = \frac{{\frac{1}{{{\beta_{{n + 1}}}{\eta_{{n + 1}}}}} + \sum_{{i = 1}}^n\frac{1}{{{\beta_i}{\eta_i}}}}}{{\frac{1}{{{\eta_{{n + 1}}}}} + \left( {\sum_{{i = 1}}^n\frac{1}{{{\eta_i}}}} \right) - 1}} < \frac{{\frac{{g\left( {{{\overline {{\bf p}} }_n}} \right)}}{{{\eta_{{n + 1}}}}} + \sum_{{i = 1}}^n\frac{1}{{{\beta_i}{\eta_i}}}}}{{\frac{1}{{{\eta_{{n + 1}}}}} + \left( {\sum_{{i = 1}}^n\frac{1}{{{\eta_i}}}} \right) - 1}} = g\left( {{{\overline {{\bf p}} }_n}} \right), $$

where the final equality follows from

$$ a = \frac{b}{c} \Rightarrow a = \frac{{\frac{a}{x} + b}}{{\frac{1}{x} + c}} $$

for any x.

Appendix III: Local stability analysis for the two-species case

We complete the stability analysis for the two-species case started in the main text. Let ${\eta_i} = {\gamma_i}/{\alpha_i}{\beta_i}$. We want to show that

$$ {m_{\rm{crit}}} = \frac{{2{{\left( {{\alpha_2}{\beta_2}{\gamma_1} + {\alpha_1}{\beta_1}{\gamma_2} - {\gamma_1}{\gamma_2}} \right)}^2}}}{{\left( {{\alpha_1}\left( {{\beta_2} - {\beta_1}} \right) + {\gamma_1}} \right)\left( {{\alpha_2}\left( {{\beta_1} - {\beta_2}} \right) + {\gamma_2}} \right)\left( {{\alpha_2}{\beta_1}{\gamma_1} + {\alpha_1}{\beta_2}{\gamma_2} - {\alpha_1}{\alpha_2}{{\left( {{\beta_1} - {\beta_2}} \right)}^2}} \right)}} > 1. $$

Note that the three factors in the denominator of m _crit are positive and the parenthetic expression in the numerator is positive too because:

$$ {\alpha_2}{\beta_2}{\gamma_1} + {\alpha_1}{\beta_1}{\gamma_2} - {\gamma_1}{\gamma_2} = {\alpha_2}{\beta_2}{\gamma_1} + {\gamma_2}{s_{{11}}} $$

Now let:

$$ A = 2{\left( {{\alpha_2}{\beta_2}{\gamma_1} + {\alpha_1}{\beta_1}{\gamma_2} - {\gamma_1}{\gamma_2}} \right)^2} > 0 $$

$$ B = \left( {{\alpha_1}\left( {{\beta_2} - {\beta_1}} \right) + {\gamma_1}} \right)\left( {{\alpha_2}\left( {{\beta_1} - {\beta_2}} \right) + {\gamma_2}} \right)\left( {{\alpha_2}{\beta_1}{\gamma_1} + {\alpha_1}{\beta_2}{\gamma_2} - {\alpha_1}{\alpha_2}{{\left( {{\beta_1} - {\beta_2}} \right)}^2}} \right) > 0 $$

So we have:

$$ \matrix{ {A - B = 2{{\left( {{\alpha_2}{\beta_2}{\gamma_1} + {\alpha_1}{\beta_1}{\gamma_2} - {\gamma_1}{\gamma_2}} \right)}^2}} \hfill \cr { - \left( {{\alpha_1}\left( {{\beta_2} - {\beta_1}} \right) + {\gamma_1}} \right)\left( {{\alpha_2}\left( {{\beta_1} - {\beta_2}} \right) + {\gamma_2}} \right)\left( {{\alpha_2}{\beta_1}{\gamma_1} + {\alpha_1}{\beta_2}{\gamma_2} - {\alpha_1}{\alpha_2}{{\left( {{\beta_1} - {\beta_2}} \right)}^2}} \right)} \hfill \cr { = - \left\{ { - {\alpha_1}{\alpha_2}{{\left( {{\beta_1} - {\beta_2}} \right)}^2} + {\alpha_2}\left( {{\beta_1} + {\beta_2}} \right){\gamma_1} + {\alpha_1}\left( {{\beta_1} + {\beta_2}} \right){\gamma_2} - {\gamma_1}{\gamma_2}} \right\}} \hfill \cr { \times \left\{ { - {\alpha_1}{\alpha_2}{{\left( {{\beta_1} - {\beta_2}} \right)}^2} + {\alpha_1}\left( { - 2{\beta_1} + {\beta_2}} \right){\gamma_2} + {\gamma_1}\left( {{\alpha_2}\left( {{\beta_1} - 2{\beta_2}} \right) + 2{\gamma_2}} \right)} \right\}} \hfill \cr }<!end array> $$

The first factor in braces here is positive because:

$$ \matrix{ { - {\alpha_1}{\alpha_2}{{\left( {{\beta_1} - {\beta_2}} \right)}^2} + {\alpha_2}{\beta_1}{\gamma_1} + {\alpha_2}{\beta_2}{\gamma_1} + {\alpha_1}{\beta_1}{\gamma_2} + {\alpha_1}{\beta_2}{\gamma_2} - {\gamma_1}{\gamma_2}} \hfill \cr { = \left\{ {{\alpha_2}{\beta_1}{\gamma_1} + {\alpha_1}{\beta_2}{\gamma_2} - {\alpha_1}{\alpha_2}{{\left( {{\beta_1} - {\beta_2}} \right)}^2}} \right\} + \left\{ {{\alpha_2}{\beta_2}{\gamma_1} + {\alpha_1}{\beta_1}{\gamma_2} - {\gamma_1}{\gamma_2}} \right\}} \hfill \cr { = \left\{ {\left( {{\alpha_1}\left( {{\beta_2} - {\beta_1}} \right) + {\gamma_1}} \right)\left( {{\alpha_2}\left( {{\beta_1} - {\beta_2}} \right) + {\gamma_2}} \right)} \right\}} \hfill \cr { + 2\left\{ {{\alpha_1}{\beta_1}{\alpha_2}{\beta_2} - \left( {{\alpha_1}{\beta_1} - {\gamma_1}} \right)\left( {{\alpha_2}{\beta_2} - {\gamma_2}} \right)} \right\}} \hfill \cr { = \left( {{s_{{21}}} - {s_{{11}}}} \right)\left( {{s_{{12}}} - {s_{{22}}}} \right) + 2\left\{ {{\alpha_1}{\beta_1}{\alpha_2}{\beta_2} - \left( {{\alpha_1}{\beta_1} - {\gamma_1}} \right)\left( {{\alpha_2}{\beta_2} - {\gamma_2}} \right)} \right\} > 0} \hfill \cr }<!end array> $$

The second factor in the expression for A − B is negative because:

$$ \matrix{ { - {\alpha_1}{\alpha_2}{{\left( {{\beta_1} - {\beta_2}} \right)}^2} + {\alpha_1}\left( { - 2{\beta_1} + {\beta_2}} \right){\gamma_2} + {\gamma_1}\left( {{\alpha_2}\left( {{\beta_1} - 2{\beta_2}} \right) + 2{\gamma_2}} \right)} \hfill \cr { = \left( {{\alpha_1}{\beta_1} - {\gamma_1}} \right)\left( {{\alpha_2}{\beta_2} - {\gamma_2} - {\alpha_2}{\beta_1}} \right) + \left( {{\alpha_2}{\beta_2} - {\gamma_2}} \right)\left( {{\alpha_1}{\beta_1} - {\gamma_1} - {\alpha_1}{\beta_2}} \right)} \hfill \cr { = {s_{{11}}}\left( {{s_{{22}}} - {s_{{12}}}} \right) + {s_{{22}}}\left( {{s_{{11}}} - {s_{{21}}}} \right) < 0} \hfill \cr }<!end array> $$

and so $A - B > 0$. We know that B is positive, so ${m_{\rm{crit}}} = A/B > 1$.

Appendix IV: Jacobian for the general case

We want to compute the Jacobian A evaluated at the equilibrium (3) of the dynamical system defined by (2). Let ${\eta_i} = {\gamma_i}/{\alpha_i}{\beta_i}$. To do this, we require the partial derivatives of the expression on the right hand side of the master equation (2):

$$ {F_i}\left( {{\bf p}} \right) = \left( {1 - m} \right){p_i} + m{p_i}\left\{ {\frac{{ - {\gamma_i}{p_i}}}{{{\alpha_i}f\left( {{\bf p}} \right) - {\gamma_i}{p_i}}} + {\beta_i}g\left( {{\bf p}} \right)} \right\} $$

where

$$ f\left( {{\bf p}} \right) = \sum\limits_k {{\beta_k}{p_k}} $$

and so

$$ \frac{{\partial f}}{{\partial {p_i}}} = {\beta_i} $$

and

$$ g\left( {{\bf p}} \right) = \sum\limits_j {\frac{{{\alpha_j}p_j}}{{\left( {{\Sigma_k}{\alpha_j}{\beta_k}{p_k}} \right) - {\gamma_j}{p_j}}}} = \sum\limits_j {\frac{{{\alpha_j}{p_j}}}{{{\alpha_j}f\left( {{\bf p}} \right) - {\gamma_j}{p_j}}}} $$

and so

$$ \matrix{ {\frac{{\partial g}}{{\partial {p_i}}} = \frac{{\alpha_i^2}}{{{{\left( {{\alpha_i}f\left( {{\bf p}} \right) - {\gamma_i}{p_i}} \right)}^2}}}\left( {f\left( {{\bf p}} \right) - {p_i}\frac{{\partial f}}{{\partial {p_i}}}} \right) - \frac{{\partial f}}{{\partial {p_i}}}\sum\limits_{{j \ne i}} {\frac{{\alpha_j^2{p_j}}}{{{{\left( {{\alpha_j}f\left( {{\bf p}} \right) - {\gamma_j}{p_j}} \right)}^2}}}} } \hfill \cr { = \frac{{\alpha_i^2\left( {{\bf p}} \right)}}{{{{\left( {{\alpha_i}f\left( {{\bf p}} \right) - {\gamma_i}{p_i}} \right)}^2}}} - {\beta_i}\sum\limits_j {\frac{{\alpha_j^2{p_j}}}{{{{\left( {{\alpha_j}f\left( {{\bf p}} \right) - {\gamma_j}{p_j}} \right)}^2}}}} } \hfill \cr }<!end array> $$

These expressions can be used to compute the partial derivatives of F _i :

$$ \frac{{\partial {F_i}}}{{\partial {p_i}}} = 1 + m\left\{ {\frac{{ - {\alpha_i}f\left( {{\bf p}} \right)}}{{{\alpha_i}f\left( {{\bf p}} \right) - {\gamma_i}{p_i}}} + {\beta_i}g\left( {{\bf p}} \right) + {p_i}\left[ {\frac{{{\alpha_i}{\gamma_i}}}{{{{\left( {{\alpha_i}f\left( {{\bf p}} \right) - {\gamma_i}{p_i}} \right)}^2}}}\left( {{p_i}{\beta_i} - f\left( {{\bf p}} \right)} \right) + {\beta_i}\frac{{\partial g}}{{\partial {p_i}}}} \right]} \right\} $$

and

$$ \frac{{\partial {F_i}}}{{\partial {p_j}}} = m{p_i}\left\{ {\frac{{{\alpha_i}{\gamma_i}}}{{{{\left( {{\alpha_i}f\left( {{\bf p}} \right) - {\gamma_i}{p_i}} \right)}^2}}}{p_i}{\beta_j} + {\beta_i}\frac{{\partial g}}{{\partial {p_j}}}} \right\} $$

for $i \ne j$. Note that:

$$ \sum\limits_{{i = 1}}^n {\frac{{\partial {F_i}}}{{\partial {p_j}}}} = 1 $$

for any j. Intuitively, this follows because the F _i just represent all of the p _i and time t + 1 and the net change in these with a change in p _j is just one.

Now at, ${{\bf p}} = \overline {{\bf p}}$, we have:

$$ {\overline p_i} = f\left( {\overline {{\bf p}} } \right)\frac{{{\alpha_i}}}{{{\gamma_i}}}\left( {1 - \frac{1}{{{\beta_i}g\left( {\overline {{\bf p}} } \right)}}} \right) $$

and so:

$$ {\left. {\frac{{\partial g}}{{\partial {p_i}}}} \right|_{{\overline {{\bf p}} }}} = \mathop{\beta }\nolimits_i^2 \frac{{g{{\left( {\overline {{\bf p}} } \right)}^2}}}{{f\left( {\overline {{\bf p}} } \right)}} - \mathop{\beta }\nolimits_i \frac{{g\left( {\overline {{\bf p}} } \right)}}{{f\left( {\overline {{\bf p}} } \right)}}h\left( {\overline {{\bf p}} } \right) $$

where

$$ h\left( {\overline {{\bf p}} } \right) = \sum\limits_k {\left\{ {\frac{{{\alpha_k}{\beta_k}}}{{{\gamma_k}}}\left( {{\beta_k}g\left( {\overline {{\bf p}} } \right) - 1} \right)} \right\}} $$

and:

$$ {\left. {\frac{{\partial {F_i}}}{{\partial {p_j}}}} \right|_{{\overline {{\bf p}} }}} = m\frac{{{\alpha_i}}}{{{\gamma_i}}} - \left( {{\beta_i}g\left( {\overline {{\bf p}} } \right) - 1} \right){\beta_j}\left\{ {\left( {{\beta_i} + {\beta_j}} \right)g\left( {\overline {{\bf p}} } \right) - 1 - h\left( {\overline {{\bf p}} } \right)} \right\} $$

for i ≠ j, and

$$ \eqalign{ {\left. {\frac{{\partial {F_i}}}{{\partial {p_i}}}} \right|_{{\overline {{\bf p}} }}} = 1 + m{p_i}\beta_i^2\left\{ {\frac{{g\left( {\overline {{\bf p}} } \right)}}{{f\left( {\overline {{\bf p}} } \right)}}\left( {{\beta_i}g\left( {\overline {{\bf p}} } \right) - 1 - \frac{{{\gamma_i}}}{{{\alpha_i}}}g\left( {\overline {{\bf p}} } \right)} \right) + \left( {{\beta_i}\frac{{g{{\left( {\overline {{\bf p}} } \right)}^2}}}{{f\left( {\overline {{\bf p}} } \right)}} - \frac{{g\left( {\overline {{\bf p}} } \right)}}{{f\left( {\overline {{\bf p}} } \right)}}h\left( {\overline {{\bf p}} } \right)} \right)} \right\} = \hfill \cr = 1 + m\frac{{{\alpha_i}}}{{{\gamma_i}}}\left( {{\beta_i}g\left( {\overline {{\bf p}} } \right) - 1} \right){\beta_i}\left\{ {\left( {2{\beta_i} - \frac{{{\gamma_i}}}{{{\alpha_i}}}} \right)g\left( {\overline {{\bf p}} } \right) - 1 - h\left( {\overline {{\bf p}} } \right)} \right\} \hfill \cr }<!endgathered> $$

We can then write a general expression for the entries of the Jacobian A:

$$ {a_{{ij}}}{\left. { = \frac{{\partial {F_i}}}{{\partial {p_j}}}} \right|_{{\overline {{\bf p}} }}} = {\delta_{{ij}}} + m\frac{{{\alpha_i}}}{{{\gamma_i}}}\left( {{\beta_i}g\left( {\overline {{\bf p}} } \right) - 1} \right){\beta_j}\left\{ {\left( {{\beta_i} + {\beta_j} - {\delta_{{ij}}}\frac{{{\gamma_i}}}{{{\alpha_i}}}} \right)g\left( {\overline {{\bf p}} } \right) - 1 - h\left( {\overline {{\bf p}} } \right)} \right\} $$

where δ _ij is the Kronecker delta. Note that ${\beta_i}g\left( {\overline {{\bf p}} } \right) - 1 > 0$ because this is a necessary and sufficient condition for coexistence, as discussed in the main text.