Building energy modeling at neighborhood scale

Abstract

The urban climate and outdoor air quality of cities that have a positive thermal balance depending on the thermal consumptions of buildings cause an increase of the urban heat island and global warming effects. The aim of this work has been to develop an energy balance using the energy consumption data of the district heating network. The here presented engineering energy model is at a neighborhood scale, and the energy-use results have been obtained from a heat balance of residential buildings, by means of a quasi-steady state method, on a monthly basis. The modeling approach also considers the characteristics of the urban context that may have a significant effect on its energy performance. The model includes a number of urban variables, such as solar exposition and thermal radiation lost to the sky of the built environment. This methodology was applied to thirty-three 1 km × 1 km meshes in the city of Turin, using the monthly energy consumption data of three consecutive heating seasons. The results showed that the model is accurate for old built areas; the average error is 10% for buildings constructed before 1970, while the error reaches 20% for newer buildings. The importance and originality of this study are related to the fact that the energy balance is applied at neighborhood scale and urban parameters are introduced with the support of a GIS tool. The resulting engineering models can be applied as a decision support tool for citizens, public administrations, and policy makers to evaluate the distribution of energy consumptions and the relative GHG emissions to promote a more sustainable urban environment. Future researches will be carried out with the aim of introducing other urban variables into the model, such as the canyon effect and the presence of vegetation.

Introduction

New urban development is an opportunity to combat climate change and to create new livable and energy efficient urban areas in order to obtain better environmental sustainability (Dogan and Reinhart 2017). Cities around the world have begun to set targets for the reduction of greenhouse gas (GHG) emissions in order to achieve low environmental impacts and to address climate change (Sokol et al. 2017). The energy consumption of buildings has a significant impact on urban sustainability and climate change, and these phenomena are more pronounced in high-density urban contexts. Cities are responsible for 75% of GHG emissions, and the building and transport sectors are the main contributors (UNEP 2018). In recent years, the obtained data have showed that global energy-related carbon dioxide (CO₂) emissions rose in 2018, increasing by 1.7%, following a 1.6% increase in 2017 from the previous year. The building sector accounted for about 28% of the total energy-related CO₂ emissions, and buildings will play a central role in the transition to clean energy (IEA 2019).

In Italy and in most European countries, energy policies are focused on two prior actions to reduce energy consumption and GHG emissions: an improvement in energy efficiency and an exploitation of the available renewable energy sources (Mutani and Todeschi 2018). In order to achieve energy sustainability in urban contexts, a number of solutions may be adopted, such as the distribution of heat through a district heating network (DHN), the use of building envelopes and urban spaces to produce energy from renewable sources, and a mix of user types with a different daily energy load in the same areas. The limited availability of renewable energy sources (RES) in urban contexts leads to the need for a combination of these solutions, with strategies to reduce, manage, and monitor energy uses (Mutani et al. 2018b). The balance of energy demand and supply should be at the smallest scale possible: at a building, block of buildings, or district scale rather than at an urban or territorial scale (Mutani and Todeschi 2017). However, there is no one-solution strategy in energy planning at an urban or territorial scale because each and every city, built environment and population is different.

Energy consumption models can be of help in describing the use of energy and GHG emissions in a real context, and they can take into account cultural differences that may influence the choice of energy retrofitting measures or the use of RES. These models can also be used to evaluate future scenarios and the impact of potential retrofitting measures as well as to identify the critical areas where a priority of interventions is required (Mutani et al. 2018a). The energy performance of buildings is influenced by several factors, such as the building shape and their typological characteristics, the heating and cooling system efficiencies, the type of users, and the behavior of the people therein, but also by the urban context and the local microclimate (Lauzet et al. 2019). The Urban-Scale Energy Modeling (USEM) is fundamental to simulate energy consumption at urban scale taking into account not only characteristics at building level but also the built-up urban context (Mutani and Todeschi 2019). USEMs usually utilize three approaches: top-down, bottom-up, and hybrid (Li et al. 2017; Carozza et al. 2017), and, in general, it is possible to identify a reliable energy model if the input database is accurate and complete and if the results can be compared with wide-ranging data on measured energy consumptions to validate the model (Reinhart and Cerezo 2016). The main problem of these models at an urban scale is that they need to manage a large number of data which may have different levels of accuracy and scales (to describe the characteristics of all the buildings and people throughout a territory); furthermore, they should also process data quickly (Ryan and Sanquist 2012).

Geographic Information Systems (GIS) are able to geo-reference all the information on energy-related variables at a territorial scale, and they can play a key role in the identification and application of energy models at an urban scale (Nageler et al. 2017). GIS tools can also help decision-makers and urban planners by offering them the opportunity to visualize realistic and multilayer representations of urban energy consumptions and spatiotemporal parameters, as well as of performing qualitative and quantitative analysis with different scenarios for future smart and more sustainable cities (Alhamwi et al. 2017; Caputo and Pasetti 2017).

Literature review

In an urban context, the energy consumption of a building stock is affected by several factors, such as the design of the built environment, the relationship between the buildings and open spaces, the type of materials used for the external surfaces, the socio-economic characteristics of the population, the type of obstructions, and, naturally, the climate and microclimate conditions (Delmastro et al. 2015; Martin et al. 2017; Mutani et al. 2016). Since the relationship between urban form and buildings affects the energy performances, it is therefore possible to obtain a lower energy demand by improving the morphology of the built environment (Gobakis and Kolokotsa 2017). The shape and heights of buildings may affect their solar exposition, with consequences on the solar heat gains and the energy produced by envelope-integrated photovoltaic modules and solar collectors (Shi et al. 2017). The spatial configuration of the built environment can be described using three energy-related parameters: the buildings “surface-to-volume” (S/V) ratio, the canyon “height-to-width” (H/W) ratio, and the “main orientation of the streets” (MOS); these parameters express the compactness of the built environment and the type of the surrounding open spaces (Xu et al. 2019). Compact urban configurations (with low S/V ratios) reduce the heat exchanges between the buildings and the outdoor environment but also reduce the solar heat gains. The canyon H/W ratio describes the typical urban microclimates around the buildings, with urban canyons having a higher solar radiation absorption and consequently higher air temperatures, lower wind speeds, and worse air quality (Afiq et al. 2012). The MOS also influences the solar absorption in an urban canyon, with limited shade for an East-West orientation and more shade for a North-South orientation. When an East-West orientation is not attainable, achieving high compactness, by keeping the S/V ratio low, becomes an important low-energy design strategy (Vartholomaios 2017; Mutani et al. 2017).

Finally, USEMs also take into account the effects of the building occupants on energy-use. Building energy-use is affected by the behavior of the occupants (Barbour et al. 2019), as they adjust the air temperature set point, which results in different daily schedules of the heating/cooling and electrical appliances (Ryan and Sanquist 2012).

Research background and gap

The investigation of USEMs is a goal of many research groups, and there are a number of simulation energy tools and techniques (i.e., CitySim, UrbanSim “UCB”, Urban Modeling Interface “UMI”) able to estimate building stock energy demand considering urban climate and morphology (Bruse et al. 2015; Sola et al. 2018, 2019). As mentioned before, the problem of this kind of tools is that they require a large amount of input data and often some information are not available; in addition, these energy models only consider a few of the variables that influence consumption, especially as regards the urban context (Li et al. 2004). However, existing models and tools have limitations in representing a realistic urban energy distribution able to assess the energy performance at neighborhood scale (Abbasabadi and Ashayeri 2019). In fact, the simulation programs consist of an assemblage of different sub-models (Sola et al. 2018) and are time-consuming processes. Research should be dedicated to the construction of an engineering model that considers several possible factors to describe the urban environment, in order to have a flexible, fast, and easy approach that may be applied to different contexts.

In the following sub-sections, the following topics have been investigated: the main existing urban-scale energy simulation models and tools (“Energy-use models and tools” section), tools used for mapping and planning the distribution of energy consumption at different scales (“2D and 3D models for mapping energy consumptions” section), the analysis of urban climate in relation to energy performance of building to reduce UHI effect and identifying effective energy policies (“Urban heat island mitigation” section).

Energy-use models and tools

Following a few studies regarding approaches (top-down, bottom-up, statistical), instruments (CityGML, Rhino), and tools (CitySim, GIS, UMI) used to support the creation of USEMs are reported.

Puglisi et al. (2016) described a method that could be used to estimate the energy consumed for heating, cooling, and domestic hot water, and created monthly load profiles for residential dwellings. In particular, they developed dynamic building energy performance models that take into account the variability of the climate conditions and the internal heat loads. The methodology allowed the types of dwelling to be grouped into 20 clusters, as a function of the building and environmental characteristics. Roulet (2002) analyzed the energy balance by taking into account internal and external temperature variations and through a utilization factor of the dynamic effect of internal and solar gains. The calculation method refers to ISO 13970 standards. The author evaluated the heat losses of a building when heated at a constant internal temperature, the internal and passive solar heat gains and the annual heat required to maintain the comfort set-point temperature in the building.

Chen et al. (2017) investigated the energy consumption considering building characteristics and shading buildings, shared walls, and weather conditions. They introduced the CityBES tool to assess energy retrofit analysis, identifying energy efficiency measures to improve energy performance of a large number of buildings in cities. A bottom-up modeling approach for urban-scale analysis was developed by Hedegaard et al. (2019), and the district heating consumptions of residential buildings were investigated using smart-meter data, building characteristics, and climate conditions. Their model was able to analyze the demand response potential investigating how to reduce the peak. USEMs have to also take into consideration the presence of vegetation and trees, which affect the urban microclimate. Perera et al. (2018) propose an approach that, with the use of CitySim tool, allows to analyze the peak and the annual demand related to the urban climate. They found that neglecting the urban climate could cause a drop in power reliability.

2D and 3D models for mapping energy consumptions

The outputs of the urban-scale energy models allow to visualize the distribution of energy consumption, identifying for example the most critical areas (high consumption), and in these urban areas, the thermal comfort conditions are scares compared to other ones. Below are indicated some studies that, after the application of USEMs, map energy consumption at territorial scale, using for example 3D-city models.

Johansson et al. (2017) created an energy atlas of the multifamily building stock in Sweden to enable estimations of the costs, the effects on energy-use, and the socio-economic features associated with possible renovation strategies. The atlas was developed using extract, transform, and load technology to aggregate information on the energy building performance, ownership, renovation status, and socio-economic characteristics of inhabitants from various data sources. Belussi et al. (2017) mapped the energy consumption of buildings, at an urban scale, using a bottom-up and top-down methodology, which was based on information provided by an open-source database on geometrical, morphological, and typological characteristics (TABULA and Energy Performance Certificates data). A statistical approach was adopted, and the energy performances were calculated according to building characteristics (i.e., volume, S/V, thermal transmittance). Also, Mutani and Todeschi (2017) assessed the annual thermal consumption of buildings applying a hybrid energy model. This model uses a statistical approach to identify energy-dependent urban-scale variables such as the period of construction and on the compactness of the buildings.

More recently, Mutani et al. (2018a) and Boghetti et al. (2019) compared various tools and models in order to easily describe the distribution of energy consumption at urban scale taking into account the characteristics of the built-up environment. The energy consumptions in some districts have been mapped with a 3D city model using GIS tool. Sokol et al. (2017) introduced an urban building energy modeling using a new Bayesian approach. Their model allows calibrating building archetypes to model small residential and commercial building stocks, and the results were mapped using a 3D city model. Monteiro et al. (2017) developed a 3D model, and the energy simulation was made to identify the reference value for different building types and estimate the total urban energy consumption. Li et al. (2018) classified residential building archetypes developing a bottom-up energy modeling at district level. With the support of UMI, the distribution of energy consumptions has been investigated at territorial scale. The novelty of this approach was that the building characteristics were collected using freely available satellite images and the results.

Urban heat island mitigation

Since the increase in energy consumption of buildings contribute to the growth of the urban heat island (UHI) phenomenon (Mutani and Todeschi 2020), it is of utmost importance to estimate the real energy needs of the building sector and its spatial distribution in order to promote effective energy policies.

In order to effectively identify countermeasures to reduce UHI effects, it is necessary to evaluate the factors that influence the urban climate the most (Yang et al. 2015). Lun et al. (2013) presented some countermeasures against UHI effects, based on a 3D heat balance of an urban space. The heat balance of an urban space is a complicated system which involves various variables, such as the wind characteristics, turbulent diffusion, and the anthropogenic heat release. Lun et al. (2013) introduced a new heat balance method that considers the heat fluxes that enter and exit from the surfaces of a control volume—for the central part of a city—and heat generation and storage. In another research, Palme et al. (2017) proposed a methodology to consider the UHI effect in building performance simulations; they identified the main urban and climatic parameters in order to estimate the cooling demand of different types of residential buildings. They also estimated the uncertainty of building energy performances, due to the effect of UHI; two of main factors that can influence UHI are the wind direction and its velocity. Perera et al. (2018) considered the influence of the urban climate on the urban energy demand in an energy system design process. They introduced a novel computational platform to combine an urban climate model with a building simulation tool and an energy system optimization model. The results confirmed that the urban climate has a notable impact on the energy demand and therefore on the design of an energy system.

Research objectives

This work presents a new urban energy top-down engineering model that considers not only the characteristics of buildings but also the urban context. The model has been designed to use the energy balance equations at building scale and applied them at neighborhood scale. The here presented calculation method refers to the ISO 52016-1:2017, ISO 52017-1:2017, and ISO 13790:2008 standards, but it is applied to the neighborhood scale. In particular, starting from the existing energy balance at building scale, a new engineering model at district scale was described introducing urban data and variables. An urban energy balance model—created with the support of a GIS tool (ArcGIS 10.7)—is presented in this work, with reference to a case study of Turin. The space heating energy consumptions of buildings have been estimated considering the thermal balance of the built environment for forty-eight 1 km × 1 km areas in the city of Turin. The top-down engineering model was validated considering the measured data, the characteristics of the residential built environment in each area, and their urban features.

The novelty of this urban energy model is that it adds a number of variables to the energy balance of the built environment to take into account the urban context: thermal radiation lost to the sky of the built environment was quantified through the use of the sky view factor (SVF), and solar exposition was described considering information pertaining to the main orientation of the streets (MOS) and the relative height of the district with respect to its surroundings (H/H_avg). Other energy simulation tools (as CitySim) used different tools as CityGML and Rhino, which are much more complex and time consuming. Instead, the use of GIS tool is very flexible consenting to manage data with different scales. Since this model was created according to standard balance equations, this makes the model flexible and easily applicable to other contexts. The main data of built environment are available for both urban and non-urban territories within the technical maps using ArcGIS 10.7. If some input data are missing, it is possible to use the standard data indicated in the regulations or in the literature.

The paper is structured as follow: the third section (“Materials and Methods” section) presents the methodology that was used to evaluate the energy balance of the thermal energy consumptions of buildings at a district scale, describes the data-input, and identifies the building and urban variables utilized to create the model. A case study, to which the model was applied is then presented in the “Case study” section. The results of the application of the model to the city of Turin are discussed in the “Results and discussion” section, and the conclusions and possible future developments of this research are indicated in the “Results and discussion” and “Conclusions” section.

Materials and methods

The presented methodology is an energy balance at neighborhood scale of the thermal energy consumptions of buildings connected to the DHN, in which the used measured energy data refer to three heating seasons (2012/2013, 2013/2014, and 2014/2015), and where different characteristics of the buildings, starting from the type of users, were considered. Monthly data about the energy consumption of the buildings (for space heating and domestic hot water) were provided for forty-eight 1 km² meshes in the city of Turin by the Iren DH Company (the local DH company). The energy consumption model used in this work for space heating and domestic hot water was set up considering the energy balance indicated in the ISO EN 52016-1:2017 and ISO EN 52017-1:2017 standards for residential buildings, and considering the following characteristics, which were elaborated by means of a GIS tool (ArcGIS 10.7) at a building and district scale:

• Building characteristics (heated volume, type of building, period of construction, S/V ratio, net floor surface, opaque and transparent envelope type, and area);

• Characteristics of the heating system (centralized or autonomous system, system efficiencies, type of energy vector);

• Climate and microclimate conditions (air temperature, air relative humidity, solar irradiance, heating degree days), distinguishing between the average monthly data for Turin and the monthly data of the nearest weather station (WS) in order to characterize the microclimate of the different urban built-up areas;

• Urban morphology (solar exposition, streets orientation, and SVF).

The described model classifies residential buildings according to the type of consumption (space heating “H” or domestic hot water “H + DHW” consumptions). The data provided by the Iren DH Company for each mesh were divided into H consumption and H + DHW consumption. This distinction was made after having analyzed the consumption data: the meshes in which consumption was known in the summer months were identified as H + DHW, while the meshes in which consumption was only known for the winter season were classified as H.

Only residential buildings were considered in this model. The percentage of residential buildings located in each mesh was calculated, and this percentage was applied to the total energy consumption data in order to consider only the residential quota. This methodology hypothesizes that, in each area of the city of Turin, residential buildings will have a certain consumption depending on the characteristics of the buildings, which depend mainly on the age of construction, and on the shape and orientation of the built context. Since the main quota of energy consumption is due to residential buildings, in this model, it is assumed that the other buildings have a constant specific consumption (Mutani and Todeschi 2017; Mutani et al. 2016).

To evaluate the distribution of the users related to the quota connected to the DH, the following two parameters were used:

• The percentages of residential, commercial, municipal, and industrial sectors; these values were calculated, using the Municipal Technical Map of Turin with GIS tool through the information of buildings’ volume (net and gross), area, and number of floors and type of users;

• The percentage of volumes connected to the DH; this value was calculated using the data from DH company (net volume) compared to the total volume (from GIS database) of the area.

The period of construction was mainly before 1945, 1946–1970, and 1971–1990 (Mutani and Todeschi 2017), and the buildings’ shape was quite uniform, with only large condominiums being connected to the DHN.

The adopted approach is a “top-down engineering” or hybrid model of the heat and mass flow balance which may be used to predict thermal energy use at a district scale on 1 km² sized meshes. The model is based on simplified heat transfer equations and the introduction of a number of urban variables that affect the thermal consumption of buildings. In general, standards do not consider these parameters, but this work has introduced them in order to analyze how the orientation of the building and how the relationship between a building and its surrounding context influence the energy performances. For this reason, the evaluation of the energy consumption models for space heating and domestic hot water utilization was carried out taking into account the variability of the external climatic conditions, the characteristics of the residential buildings and their surroundings, and the monthly data of energy consumptions for the heated volumes of residential buildings in the 1 km² sized meshes. The heat and mass flows of the thermodynamic system are presented in Fig. 1 with the control surface and the main characteristics of the building stock and the surroundings. The energy-related variables that have not been used in this model have red dotted line; these parameters will be inserted in future works.

Fig. 1

Scheme of heat and mass flows of the thermodynamic system of the building stock at a neighborhood scale with the control surface (black line) between the building stock and the outdoor environment

The energy performances of buildings are mainly influenced by the climatic and microclimatic conditions, and the weather data (air temperature, relative humidity, and solar radiation) associated with each mesh therefore refer to both the average climatic data and the nearest WS. The methodology described in this work was focused on obtaining the following monthly energy balance for space heating and domestic hot water production for each homogeneous group of buildings:

• The thermal energy demand of the building envelopes, with heat dispersion for transmission and ventilation, and the solar and internal heat gains, considering the thermal transmittance values of the envelope, the air flow rate, the solar shadings, and the internal heat gains;

• The energy supplied to the buildings, taking into account the efficiency of space heating (H) and domestic hot water (DHW) systems. The distribution losses of the DHN are not considered because the energy meters are located near each building. Then, the efficiency of the systems considers the generation and utilization components, respectively from the point of delivery of the building to the distribution system and from the distribution system to the emission system.

The presented method (Fig. 2) involves the calculation of the energy demand of and supply to residential buildings necessary to guarantee internal air temperature comfort conditions at a temperature of 20 °C during the heating season, and the annual domestic hot water demand. This methodology adapts the energy balance equations at a building scale, described by the ISO 52016-1:2017 standard (the thermal energy demand for humidification and dehumidification is not considered), to the district scale for each 1 km² mesh of Turin, taking into account the availability of the data at an urban level. Therefore, some variables used in the ISO 52016-1:2017 standard were modified to describe the phenomenon at a larger scale. Three urban variables (see Fig. 2) were in particular added to the energy balance equations at an urban scale: the SVF, the MOS, and H/H_avg. These urban parameters were introduced in order to evaluate the solar exposition and heat dispersion of each mesh. Figure 2 shows the process from the data input to the pre-processing to the simulation procedure:

• Data input refers to the buildings, climate, and urban morphology characteristics; Fig. 2 shows all the data that should be considered to create the model, but only a number of the indicated urban parameters (those indicated with an “x”) were considered in this first work;

• In the pre-processing phase, the input data were elaborated and associated to each mesh;

• The simulation results were compared with the measured data, for validation purposes, and the model was calibrated with a number of urban variables to optimize the model and reduce the error.

Fig. 2

Flowchart of the methodology: data input (building data, climate data, and urban morphology data), pre-processing (mesh scale data), and simulation (calibration and validation on each mesh)

In particular, the data input have been elaborated with GIS tool (ArcGIS 10.7), and a database was created using the municipal technical map, the territorial database of the region, the socio-economic data (ISTAT census database), the WS measurements (heating degree days “HDD,” air temperature, relative humidity, solar radiation), satellite images (Landsat 8) with a precision of 30 m available from USGS website, a Digital Surface Model (DSM) of Turin with a precision of 5 m provided by Piedmont Region, and the monthly energy consumption data provided by the Iren DH Company of Turin.

An iterative procedure was performed on Excel spreadsheets (“Validation” in Fig. 2), in order to reduce the error of the energy consumptions, using the following quality measures:

• The error, E, is used to compare the results of the model (forecast values) with the measured data;

• The relative error Er and the absolute relative error |Er|: Er is calculated by the difference between measured and forecast value, divided by the measured value; |Er| is the measure of the prediction accuracy of the model and is the absolute value of the relative error;

• The coefficient of determination (R²), which is a key output to compare calculated and measured data, was used as a guideline to establish the accuracy of the model.

The joint use of these types of error allows to take into account both the absolute values and the percentage differences between calculated and measured data but also to consider “acceptable” higher percentage errors if the absolute consumption value is very low.

In the last part of this work, to understand how the urban form influences the energy consumption of residential buildings, some simulations were made using the variability of some urban variables: SVF and MOS. Four scenarios were investigated considering different levels of unfavorable and favorable conditions.

Description of the energy balance equations

This section describes the method used to calculate the monthly energy balance for a group of residential buildings, adapting the ISO 52016-1:2017 standard that was drafted at building scale, for a district of 1 km² at neighborhood scale. In general, this standard specifies calculation methods that can be used to assess the sensible energy needs for space heating, on the basis of monthly calculations at building scale. This calculation method can be used for residential or non-residential buildings and may be applied to buildings at the design stage, to new buildings after construction, and to existing buildings in the use phase. The novelty of the presented research is that energy balance equations usually only consider one building, then a number of urban parameters were added to adapt the energy balance at neighborhood scale (with the support of a GIS tool).

Equation 1 defines the monthly energy balance of the building stock envelope, taking into account the total heat transfer (Q_H,ht) and total heat gains (Q_gn) for space heating under different climatic conditions (ISO 52016-1:2017; ISO 13790:2008):

$$ {Q}_{H, nd}={Q}_{H, ht}-{\eta}_{H, gn}.{Q}_{gn}=\left({Q}_{H, tr}+{Q}_{H, ve}\right)-{\eta}_{H, gn}.\left({Q}_{int}+{Q}_{sol}\right) $$

(1)

The total heat transfer (Q_H,ht) is composed of the sum of the heat transfer due to transmission (Q_tr) and ventilation (Q_ve), while the heat gains are due to the internal (Q_int) and solar (Q_sol) heat components. The transmission heat transfer, between the heated space of the building stock and the external environment, is driven by the difference between the air temperature inside the heated buildings (T_i) and the external air temperature (T_e). T_i was assumed constant—since this work introduced a monthly model, and the temperature during the day varies slightly, but on average always remains constant—(20 °C). Two outdoor air temperature values were considered for T_e: the average monthly temperature of five WSs in the city of Turin and the monthly air temperature of the nearest WS in each mesh. Moreover, the utilization factor (η_H,gn) is a function of the heat flow balance through the building envelope and the thermal inertia of the building stock; it was evaluated for each month and for each mesh, according to the internal heat capacity characteristics of the building stock, considering the different periods of construction.

In this work, the construction characteristics of the building stocks were assumed, in consideration of the different periods of construction and the geometric features of the buildings, as evaluated with the support of a GIS tool using the municipal technical map of the city.

Equations 2 and 3 describe the total heat loss as a result of transmission and ventilation of the building stock, respectively, and considering a uniform inside air temperature of 20 °C during the heating season (τ is the number of hours) (ISO 52016-1:2017; ISO 13790:2008):

$$ {Q}_{H, tr}={H}_{tr, adj}.\left({T}_i-{T}_e\right).\tau +\left\{\sum \limits_k{F}_{r,k}.{\phi}_{r,k}\right\}.\tau -{Q}_{sol, op} $$

(2)

where

• The transmission heat transfer coefficient (H_tr,adj) was calculated considering the thermal transmittance values (U) of the buildings for different construction periods (before 1918, 1919–1945, 1946–1960, 1961–1970, 1971–1980, 1981–1990, and 1991–2005) for each mesh using the percentage quota per heated volume (Mutani and Pairona 2014; AA.VV. 2012; Mutani et al. 2020), the opaque and transparent heat dispersing areas (A), calculated by means of the GIS tool (with a constant transparent area equal to 1/8 of the building floor surface), and the unheated volumes of the attics and cellars;

• The extra heat transfer, considering the thermal radiation lost to the sky, depends on the form factor between the building stock and the sky (F_r,k) and on the thermal radiation lost to the sky (Φ_r):

$$ {F}_{r,k}={F}_{sh, ob}.\frac{1- cos\alpha}{2}=\left(\mathbf{1}+{\boldsymbol{SVF}}_{\boldsymbol{g}}\right)/\mathbf{2}.\frac{1- cos\alpha}{2} $$

(2.1)

$$ {\phi}_{r,k}={R}_{se}.{U}_{op}.{h}_r.\left({T}_e-{T}_{sky}\right) $$

(2.2)

• The form factor F_r,k depends on the SVF of the building stock and on the inclination, α, of the control surface; SVF was calculated at the ground level (SVF_g) for each mesh, and an average value of SVF was then considered at the mid-height of the buildings (considering an SVF of 1 at the building roof level);

• The thermal radiation, Φ_r,k, was calculated only considering the control surface with a constant external thermal surface resistance (R_se), which is a function of the outdoor air velocity, and an external radiative heat transfer coefficient (h_r), which is a function of the control surface emissivity and of the sky temperatures.

Moreover, in order to take into account the influence of the direct solar radiation component, Q_sol,op was multiplied by the MOS value (Eq. 2.3) for zones with low relative heights (H/H_avg < 1) and with unfavorable orientation of the streets (with MOS < 0.5), in order to consider a non-optimal solar exposure and, as a result, lower solar heat gains:

$$ {Q}_{sol, op}=\left\{\sum \limits_k{\phi}_{sol, op,k}\right\}.\tau $$

(2.3)

where

$$ {\phi}_{sol, op,k}={F}_{sh, ob, op}.{A}_{sol, op}.{I}_{sol, op}=\boldsymbol{\omega} .\left(\mathbf{1}+{\boldsymbol{SVF}}_{\boldsymbol{g}}\right)/\mathbf{2}.{A}_{sol, op}.{I}_{sol, op} $$

$$ \boldsymbol{\omega} =\left\{\begin{array}{c} MOS\ if\frac{H}{H_{avg}}<1\ and\ MOS<0.5\\ {}1\ if\frac{H}{H_{avg}}\ge 1\ or\ MOS\ge 0.5\end{array}\right.\kern0.5em ;\left( MOS=0\ \mathrm{for}\ \mathrm{a}\ \mathrm{building}\ \mathrm{axis}\ \mathrm{with}\ \mathrm{a}\ \mathrm{North}-\mathrm{South}\ \mathrm{orientation}\ \mathrm{and}\ MOS=1\ \mathrm{for}\ \mathrm{a}\ \mathrm{building}\ \mathrm{axis}\ \mathrm{with}\ \mathrm{a}\ \mathrm{West}-\mathrm{East}\ \mathrm{orientation}\right) $$

$$ {A}_{sol, op}={\propto}_{sol, op}.{R}_{se}.{U}_{op}.{A}_{op} $$

where

• The shading reduction factor (F_sh,ob,op) is a function of the external obstacles and is equal to the average value of SVF at the mid-height of the buildings;

• Solar irradiance (I_sol,op) is the amount of incident solar irradiance on the opaque envelope;

• The absorption coefficient (α_sol,op) of the opaque envelope is supposed constant and depends on the average color of the building walls;

• Thermal surface resistance (R_se) is a function of the outdoor air velocity;

• The thermal transmittance of the opaque envelope (U_op) depends on the different periods of construction;

• The opaque envelope area (A_op) is calculated by means of the GIS.

The total heat transfer (Q_H,ht) in Eq. 1 is also influenced by the ventilation heat losses (Q_H,ve):

$$ {Q}_{H, ve}={H}_{ve, adj}.\left({T}_i-{T}_e\right).\tau $$

(3)

where

$$ {H}_{ve, adj}={\rho}_a.{c}_a.\left\{\sum \limits_k{q}_{ve,k}\right\}={\rho}_a.{c}_a.\frac{n.V}{3600} $$

where the value of the heat transfer coefficient resulting from ventilation (H_ve,adj) depends on the heat capacity of the air per volume (ρ_a . c_a = 1200 J/m³/K), on the air flow rate volumes (q_ve,k), or on the hourly air exchange volumes (n).

Equations 4 and 5 describe the total heat gains (Q_gn), which are obtained by summing the internal heat gains (Q_int) and the solar heat gains (Q_sol,w) (ISO 52016-1:2017; ISO 13790:2008):

$$ {Q}_{int}=\left\{\sum \limits_k{\phi}_{\mathit{\operatorname{int}},k}\right\}.\tau =\left\{5.294.{S}_f-0.01577.{S}_f^2\right\}.\tau $$

(4)

$$ {\displaystyle \begin{array}{c}{Q}_{sol,w}=\boldsymbol{\omega} .\left\{{\sum}_k{\phi}_{sol,w,k}\right\}.\tau \\ {}{\phi}_{sol,w,k}={F}_{sh, ob,w}.{A}_{sol,w}.{I}_{sol,w}=\left(1+{\boldsymbol{SVF}}_{\boldsymbol{g}}\right)/\mathbf{2}\cdot {A}_{sol,w}.{I}_{sol,w}\\ {}{A}_{sol,w}={g}_{gl}.\left(1-{F}_F\right).{A}_w\end{array}} $$

(5)

where

• The internal heat gains, Q_int, are calculated considering the floor area of residential buildings and the average area per dwelling (with the geometrical characteristics of the building stock calculated by means of the GIS and ISTAT census data for 2011). The global value of the internal heat gains was obtained for residential buildings with a net floor area (S_f) less than or equal to 120 m² (UNI/TS 11300-1:2014 issued to implement the European Directive 2002/91/CE);

• The solar heat gains, Q_sol,w, were calculated by multiplying the heat flow rate, due to the solar heat sources, Φ_sol, by ω considering the solar exposition (as mentioned above);

• The shading reduction factor, due to the external obstructions (F_sh,ob,w), was calculated considering SVF;

• The effective glazing area (A_sol,w) pertains to the window area (A_w), the window frame factor (F_F), and the total solar energy transmittance of the glasses (g_gl) for the different construction periods of the buildings.

The energy demand for domestic hot water (Q_W) was calculated according to Eq. 6 (ISO 52016-1:2017):

$$ {\displaystyle \begin{array}{c}{Q}_{W, nd}={\rho}_w.{c}_w.\sum \limits_i{V}_{w,i}.\left({T}_{er,i}-{T}_o\right).G\\ {}{V}_{w,i}=1.067.{S}_f+36.67\end{array}} $$

(6)

where ρ_w and c_w are the density and the specific heat of water, respectively; V_w,i is the required daily volume of hot water; (T_er,i –T_o) is the difference between the hot water supply temperature (assumed equal to 40 °C, with reference to the standard condition (ISO 52017-1:2017)) and the incoming cold water temperature (assumed equal to the annual air temperature); G is the number of days of the considered calculation period (year) which, in this case, was equal to 365 days; V_w,i is the required daily hot water volume as a function of the average floor area per dwelling in each mesh; and for residential buildings, V_w,i was obtained by the standard (ISO 52017-1:2017) for apartments with net floor surfaces (S_f) of between 50 and 200 m².

Finally, the energy need (Q_H,nd and Q_w,nd) being known, the annual average values of the system efficiencies (η_H and η_W) were used to quantify the energy supplied for space heating (Q_H) and domestic hot water (Q_W) for each district (for each 1 km² mesh):

$$ Q=\frac{Q_{nd}}{\eta } $$

(7)

To exclude the quota of non-residential energy consumption, it was assumed that the non-residential users have a constant specific consumption (in kWh/m³) (Mutani and Todeschi 2017; Mutani et al. 2016); this hypothesis can be considered acceptable since the consumption provided by the Iren DH company is mainly for residential buildings.

Theoretical backgrounds

In this sub-section the comparison between the standard energy balance at building scale and the new energy balance at neighborhood scale is explained in detail. Referring to the energy balance equations for residential buildings of the new model, the various variables introduced in the neighborhood scale model are summarized in Table 1.

Table 1 Comparison between energy balance at building scale with the new model at neighborhood scale

Definition of the building characteristics

The thermo-physical and geometric parameters of the buildings in the analyzed forty-eight 1 km² sized meshes were characterized using information from the municipal technical map of the city of Turin (2015), ISTAT census data (2011), European Standards, and data from literature reviews (Mutani and Pairona 2014; AA.VV. 2012). Because of missing data or anomalies, only a certain number of meshes were analyzed to create the monthly energy models. The unused meshes were lacking in data for a few months of the three considered seasons. Therefore, of the original 48 meshes, only 33 were selected, to avoid errors in the model due to a lack of data for some months and/or due to the presence of erroneous data.

The following data were calculated for each mesh to characterize the residential buildings connected to the DHN. The geometrical data were calculated, with the support of a GIS tool, using the attribute of a 2D footprint derived from the technical map provided by the municipality of Turin. The territorial database was implemented with other official information, such as the characteristics of the territory (using the Digital Surface Model “DSM”) and the distribution of the population (ISTAT data, 2011).

Data concerning the typological characteristics of the building

• Net and gross heated volume [m³] of the buildings;

• Net and gross floor surface [m²] of the buildings; the net area was obtained by multiplying the gross area by the f_n coefficient as a function of a typical wall thickness (d_m) of the construction period;

• Heat transmission surfaces [m²] of the inferior or ground slab, of the roof or the upper slab, and of the vertical walls, but the walls adjacent to other heated buildings were not considered in the calculation; a transparent surface equal to 1/8 of the floor was assumed for the windows, according to Mutani and Pairona (2014); AA.VV. (2012);

• Solar exposure and orientation; the MOS was evaluated considering an average value at a census section scale (at a block of buildings scale);

• Shadings elements, using the DSM of Turin and the solar geometric radiation of the GIS;

• Solar reflectance of the external outdoor surfaces taken from satellite images (Mutani et al. 2019).

Data concerning the thermal and construction characteristics of the building

• Thermal transmittance (W/m²/K) of the envelope; a specific value was selected for each period of construction for all the heat transmission surfaces, and an average value was associated to each district (1 km²) considering the percentage distribution of the buildings with different construction periods (Mutani and Pairona 2014; AA.VV. 2012);

• Total solar transmittance (g_gl) of the transparent envelope; only two values of g_gl were considered, with reference to the standard (ISO 52016-1:2017): for single glass and for double glass, the construction period and the maintenance level of the buildings were also taken into consideration;

• The solar radiation absorption coefficient (α_sol) of the opaque envelope was determined considering the main color of the building envelope;

• Emissivity (ε) of the envelope was assumed constant for opaque and transparent elements;

• Reduction frame factor (F_F) of the windows was supposed constant;

• Thermal capacity (C_m) (kJ/m²/K) was determined as a function of the construction period;

• System efficiencies (η) were determined for the different construction periods for the heating and domestic hot water systems, considering the typical centralized and autonomous systems that are connected to the DHN (ISO 52017-1:2017; Mutani and Pairona 2014; AA.VV. 2012).

Data concerning the use of the buildings

• Type of use, the buildings were classified as residential, municipal, tertiary, or industrial (the municipal and tertiary ones were further sub-categorized);

• Type of ventilation, natural or mechanical;

• Heating season period, which depends on the Italian climatic zone;

• Internal heat gains (Q_int), which depend on the use of the of building types (ISO 52016-1:2017).

Definition of the microclimate conditions

The microclimate conditions are influenced to a great extent by such environmental context factors as the urban morphology, the solar exposition, the type of materials of the outdoor spaces, and the presence of vegetation and/or water. In this work, the data of five WSs were used to evaluate how the urban characteristics influenced the microclimate and the energy consumptions. Two models were elaborated: one to consider the average climatic conditions of the whole Turin area and the second to use the microclimatic conditions registered by the nearest WS. Large variations in consumption, as a result of differences in the microclimatic characteristics, were not expected for the specific case study in Turin, as a result of the similar urban contexts of the analyzed areas. As shown in Fig. 3, the WSs data (air temperature) were very similar even if, in the heating season 2013–14 with 1962 HDD (WS: via della Consolata), a difference of 1 °C could influence the energy consumption of about 10%. This type of evaluation will be extended to smaller areas in the city of Turin in which the variability in the microclimatic characteristics is more significant.

Fig. 3

Distribution of the monthly WS air temperatures for the 2013/2014 season in the city of Turin (using data from five WSs)

Data concerning the climate and microclimate conditions

• Monthly average values of the outdoor air temperature (°C) taken from five WSs in Turin;

• Monthly average solar irradiance [W/m²] on the horizontal plane taken from the WSs in Turin.

Definition of the urban context characteristics

Each mesh was categorized by different urban context characteristics; the variables were evaluated using a municipal technical map (2015), ISTAT census data (2011), remote satellite images (2015), and a DSM with a precision of 5 m. A georeferenced territorial database was created with the support of a GIS tool. The urban morphology factors are shown hereafter, and in general, average values were identified for each mesh:

• Sky view factor, SVF measures the visible portion of the sky from a given location, and in this work, it was used to describe the solar exposition and the thermal radiation lost to the sky from the built environment (Middel et al. 2018; Li et al. 2004). SVF was calculated, with the support of the Relief Visualization Toolbox software (Zakšek et al. 2011), using the DSM of the city of Turin with an accuracy of 5 m. SVF_g was then calculated at the ground level, and an average value of SVF was elaborated and associated to each mesh with a GIS tool (Fig. 4). In this work, the obtained SVF was used to quantify the shading reduction factor (F_sh,ob) resulting from external obstacles and the form factor (F_r) between the buildings and the sky. The SVF was considered at a mid-height of the buildings (considering an SVF = 1 at the building roof level) and this value is constant for each month of the year.

• Albedo, A_NIR is the percentage of solar incident irradiation reflected from a surface and it varies according to the intrinsic characteristics of the materials (Dodoo et al. 2017; Mutani et al. 2019). In this work, A_NIR was considered in order to take into account how different materials used for the urban surfaces can influence the microclimate in the surrounding building context. The A_NIR was calculated from remote sensing images (Landsat 8) referring to November 2, 2015, at 10 a.m. with a percentage of cloud cover of only 3.9%; three bands (α₄, α₅, and α₇) were used to predict the A_NIR (Liang 2000). These data were assumed constant for each month of the year.

• Normalized difference vegetation index, NDVI; the presence of vegetation was evaluated with the NDVI using Landsat 8 satellite images (for November 2, 2015, at 10 a.m.). NDVI is the difference between NIR (which vegetation reflects) and RED light (which vegetation absorbs) which is obtained using the two relative bands (α₄ and α₅) (Mutani et al. 2019; Mutani and Todeschi 2020). The NDVI values vary: low values are observed for barren rock and sand areas or urban/built-up areas, with a value of zero for water and high values for vegetation.

• Canyon effect, H/W; the canyon effect can be measured using the aspect ratio, that is, the ratio between the height “H” of the urban canyon and its width “W.” Street canyons are generally classified as avenue canyons (H/W < 0.5), regular street canyons (H/W = 1), or deep street canyons (H/W > 2) (Delmastro et al. 2015).

• Relative height, H/H_avg describes solar exposition in relation to the height of the buildings.

• Building coverage ratio (BCR) and building density (BD); the BCR is defined as the percentage of built area, and the BD is defined as the ratio of the building volumes and the sample area (Wei et al. 2016; Streicher et al. 2019).

• Main Orientation of Streets, MOS; Turin is mainly East-South oriented, following the course of the Po river and facing the hills. In this study, the main orientation of the buildings was calculated considering the orientation of the streets. The optimal condition of solar exposition is the East-West axis (with MOS = 1), while the worst condition is the North-South axis (MOS = 0).

Fig. 4

a Distribution of the SVF_g, at a ground level, for the city of Turin using a DSM with a precision of 5 m × 5 m; the mesh scale used in this work is indicated on the map (1 km × 1 km size). b Zoom of mesh number 1296

Table 2 shows the main parameters that affect the thermal energy consumption of buildings; a description of each variable and the measurement unit are indicated. Previous researches confirming that certain variables, such as the climatic and microclimatic conditions, that is, the parameters calculated in this study, can influence energy consumption.

Table 2 Parameters of urban design that affect the building energy demand

Case study

The city of Turin, in the Piedmont Region, is located in the North-Western part of Italy; it is part of climate zone E with 2648 HDD (according to UNI 10349-3:2016). Averaging over the five WS considered, the HDD for the three consecutive heating seasons analyzed are 2388 HDD for 2012/2013, 2028 HDD for 2013/2014, and 2054 HDD for 2014/2015. There are about 60,000 heated buildings, of which 45,000 are residential, and the quota of heated gross volume is 232 Mm³. The residential sector is mainly made up of large and compact condominiums; in fact, more than 24,000 residential buildings (55%) have the S/V of less than 0.45 m⁻¹ (average value for Turin = 0.55 m⁻¹). The 57% of residential buildings was built before 1960, 80% of the buildings were built before 1970 (before the first Italian Law 373/1976 on buildings energy savings), 15% of the residential buildings were built between 1970 and 2000, and only 2% was built after 2006.

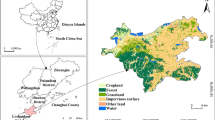
This study has investigated residential buildings connected to the Turin DHN, and the territorial analysis unit was a 1 km² mesh. A total of 28,186 heated buildings were analyzed in the 48 meshes, of which 78% (22,007) was residential buildings. The main period of construction of the residential sector is between 1946 and 1970 (52%); 7% of the residential buildings was built before 1918; 19% was built between 1919 and 1945; 11% between 1971 and 1980, and 10% after 1981 (only 2% was built after 2006). The average S/V value is 0.54 m⁻¹, and the median value is 0.44 m⁻¹; in general, the shapes of the buildings are quite homogenous in the considered areas. The residential buildings have a somewhat constant height (H_avg) of 18.5 m, and they are mainly large condominiums with low S/V values. The occupancy ratio of the residential buildings is close to 0.93, and this value is typical of the residential sector. The quota of DHW of the buildings connected to the DH network is low, around 10%, and the percentage of buildings connected to the DHN is on average 55%, but this value varies a lot depending on the zone. Finally, some meshes were excluded in this analysis (i.e., H/H + DHW) because the type of energy consumption changed in the analyzed period (only H in some seasons and H + DHW in other seasons). Since the model is based on the energy consumption of residential buildings connected to DH, the accuracy of the model will depend on the number of buildings connected to the DHN (see Appendixes 1 and 2). Figure 5 a and b show the location of the 48 meshes analyzed in this work and information about the types of energy consumption, the nearest WS, and the different types of user at a district scale; only the WSs in the built urban context of Turin were considered. Figure 5 a shows the 15 yellow meshes that were excluded from the analysis because they had some season with only H and others with H + DHW, 10 meshes with only H and 23 meshes with H + DHW. Figure 5 b shows the five WSs considered in this work: it can be observed that, for some meshes, the nearest WS does not describe the real weather conditions of the area (the station is too far away). The average Turin weather data was also used to construct the model, and the result of two models were compared to evaluate how the urban characteristics influence the microclimate and the energy consumptions. The comparison of the two models allows to understand how much the precision of the models varies according to the climate and microclimate characteristics.

Fig. 5

a Distribution of the 48 meshes (1 km²) and classification of the type of energy consumption: space heating “H” in red, space heating and domestic hot water “H + DHW” in blue, “H” and/or “H + DHW” in yellow (the identification code (ID) is inside the meshes). b Identification of the nearest WS for each mesh and distribution of the different types of user considering 4 sectors: residential (red), tertiary (yellow), municipal (blue), and industrial (violet)

Some assumptions have been made to create the monthly energy use model at a neighborhood scale. Most of Turin’s residential building stock was built before 1970 (80%), and the structural characteristics of the buildings are quite homogeneous. Therefore, it was assumed, in this study, that the analyzed residential buildings had certain factors in common (calculated using the European standards in force):

• The gross heated volumes connected to the DHN were calculated from the net volumes divided by 0.75, as specified by the DH company;

• The U was calculated for each mesh considering the percentage of building volumes for each period of construction, and an average value was identified by distinguishing between transmittance vertical walls, a transparent envelope, a floor with a basement (with an adjustment factor for unconditioned spaces, b_tr,floor = 0.8), and a ceiling with an unheated attic and an uninsulated roof (b_tr,roof = 0.9); in Table 3 the data about the thermal transmittance for the different periods of construction are reported;

• The f_n coefficient, which was used to obtain the net usable floor area from the gross area, was calculated considering the construction period of the buildings;

• The thermal capacity was assumed constant, with C_m = 165 kJ/m²/K for buildings with no or external thermal insulation, with a medium or heavy envelope, and a greater number of floors than 3;

• The average color of the opaque envelope was considered to be an average one, that is, neither dark nor clear, with a solar radiation absorption coefficient of α_sol,c = 0.6 and an emissivity ε = 0.9;

• The external surface heat resistance, R_se, was taken as 0.04 m²K/W, considering that the contribution of wind to the different areas in Turin is negligible (about 1.4 m/s, according to UNI 10349:2016);

• The window area was calculated considering 1/8 of the net floor area (according to the indications of the Italian Hygienic Standards for buildings D. M. 5/7/1975). The frame factor, F_F, was assumed constant and equal to 0.8, and the total solar energy transmittance values of the glasses, g_gl, referring to single glass (g_gl = 0.85) or to double glass (g_gl = 0.75), took into account the construction period of the buildings and their level of maintenance;

• An air exchange rate of n = 0.5–0.3 h⁻¹ was assumed for natural ventilation in residential buildings, depending on their construction period and level of maintenance;

• The heating period for the city of Turin is from October 15th to April 15th and covers a period of 183 days; the full months of October and April were introduced into the model because the systems are switched on before this date in order to have all the heating systems active on the 15th of October; the same procedure takes place for the shutdown: the systems are gradually switched off from April 15th, and the heating period is therefore generally longer;

• The average value of the usable floor area per dwelling (S_f) was used to evaluate the domestic hot water consumption of each mesh, and it was always less than 200 m² (with an average value of 88 m²);

• The internal heat gains were calculated for each mesh, considering the average floor area per dwelling as 3.9–5.2 W/m² (with an average value of 4.9 W/m²);

• The system efficiencies of the space heating and domestic hot water were calculated for each mesh, considering the connection to the DHN (in Table 3, AA.VV. 2012):

• For space heating systems: an average value was calculated for the different construction periods as “multi-unit housing” building classes; a typical heating system was considered to consist of a radiator emission system on uninsulated walls with a climate control system, a vertical distribution system with about 4 floors, and a heat exchanger as the generation system; according to the period of construction, the overall system efficiency was taken on average equal to 0.67–0.81 taking into account that the old boilers have been partially replaced with the district heating heat exchangers (according to the percentage of buildings connected to the DHN);

• For domestic hot water: the overall system efficiency of the systems was assumed to be about 0.60; the percentage of buildings connected to the DHN for this service was calculated for the consumption of DHW.

Table 3 U and η_H values for buildings with different periods of construction

Only 33 meshes with complete data on energy consumption for H and DHW from October 2012 to January 2016 were selected to create the monthly energy model. A consistent quota of residential buildings was found in most of the meshes, and the model was therefore studied for this type of user as the percentage in volume of the heated residential buildings in each mesh was known (from Municipal Technical Map data). The DH company supplied the monthly energy consumption data for each mesh and the total of the heated volumes connected to the district heating network. Two types of energy balance models were created on the basis of the type of consumption: group one had 23 meshes with information on the space heating and domestic hot water consumptions (H + DHW) and group two was composed of 10 meshes with only consumption information for space heating (H). The data on energy consumption were available for each mesh and for three consecutive heating seasons: 2012/2013, 2013/2014, and 2014/2015. The meshes with low percentages of residential buildings, especially in the peripheral areas, may yield less accurate energy performance results.

Characteristics of group 1 (consumption: H + DHW)

The first group of meshes was divided into three homogenous groups of buildings, according to their period of construction. In fact, the S/V of the residential buildings in these areas is somewhat constant, with an average value of 0.53 m⁻¹ and a standard deviation of 0.07 (i.e., large condominiums). The energy-use model of the residential buildings was analyzed considering the energy consumption of all the buildings and the proportion of residential buildings (Res) connected to the DHN.

In general, the meshes showed a high percentage of residential buildings (an average value of 72%), but there were some meshes (ID 979, 1141, 1300, 1350, 1353, and 1403) that had a smaller percentage, and this model could therefore be less accurate. The state of maintenance of the buildings was generally good, with higher values for new buildings, and the average U values were higher for the meshes with older buildings. Systems efficiency is about 72–75% depending on the percentage of buildings connected to the DHN and the different periods of construction. The BCR was higher for the residential buildings built before 1960 than for the buildings built later on, and the building density is in general greater in the central historical urban area of Turin. In addition, the H/W was also higher in the meshes with buildings built before 1960, while the H/H_avg was basically equal for all the built-up areas. The SVF_g was lower for the high-density areas and higher in the areas with a lower BCR (ID 1296, 1350, 1403, 1404) and in zones with a high presence of vegetation (high NDVI in ID: 979, 980).

Characteristics of group 2 (consumption: H)

The second homogenous group was composed of 10 meshes. In this case, due to the limited number of meshes, no subdivisions were made for the building construction periods, consequently the accuracy of this model was lower.

In this group, residential buildings were mainly built between 1961 and 1970 (6 meshes), the level of maintenance was more than sufficient, and the S/V was similar, with an average value of 0.58 m⁻¹ and a standard deviation of 0.05. The percentage of residential buildings was in general above 77% (median value), with an average value of 69%; only three meshes (ID 1034, 1402, and 1405) had a lower percentage. As already mentioned, the U and the systems efficiency (≅ 72%) depend on the period of construction. SVF_g was relatively constant, with an average value of 0.54. The presence of vegetation was somewhat scarce, since the analyzed areas are in a consolidated urban context. Three meshes (ID 1031, 1032, and 1033) had a slightly high NDVI value because they are near a park or a green area. The other urban variables showed that the areas were densely built and the buildings had similar heights (with H/H_avg of 1).

Table 4 describes the field of application of the models according to the variability of the data. The variability of the S/V, the level of maintenance (1 = very bad, 4 = optimal), BCR, H/W, H/H_avg, MOS, SVF_g, A_NIR, and NDVI are indicated for each group. It can be observed that:

• The variability of BCR and A_NIR is low because the urban context is consolidated and the territory is densely built up;

• H/W has a similar range for each group;

• The H/H_avg is close to 1, with the exception of the “H + DHW|₃” group (in which the buildings have more solar gains);

• MOS has a less variability because most of the blocks of buildings have a North-South orientation;

• Meshes located in the peripheral areas have higher SVF and NDVI values, due to the lower urban density and the greater presence of green areas and parks.

Table 4 Variability of the monthly energy balance models

These data were used in the model to evaluate how energy consumption varies for different solar exposition values (different SVF, H/H_avg, and MOS). In general, the homogeneous H groups show a lower EP than the H + DHW groups, and the consumptions are lower in the center of the city (high-density areas). As can be expected, decreasing values of BCR have been observed from the center to the peripheral areas, while rising values can be perceived for the SVF_g and H/H_avg. With regard to the MOS, the main streets in the historical center of Turin are about 30° from the North-South axis along the Po River and face the hills (see Appendix 2).

Results and discussion

This section presents and discusses the results obtained for each mesh from the application of the monthly energy balance models for the residential buildings. The data are divided into two groups: group 1, referring to the energy-use for H + DHW in 23 meshes, and group 2, referring to the energy-use for H in 10 meshes.

This results were obtained using the iterative procedure on excel spreadsheets described in Fig. 2. The model was improved by adapting the input parameters to the measured values and optimizing the errors (the relative error, the absolute relative error, and the global relative error). The iterative method has been refined starting from the energy balance equations at building scale and gradually introducing the variables that characterized the groups of buildings in the different districts. As this method was studied for residential buildings, the first meshes on which it was tested were those with a very high percentage of residential buildings. Therefore, for each construction period, the meshes with a percentage of residential buildings greater than 80% were selected starting from group 2 H with the meshes of 1961–1970: 1092, 1190, and 1297; then we moved to the meshes of 1971–80: 1031 and 1244. The same procedure was implemented with group 1 H + DHW. From the first tests, even with a very simple model, the monthly energy balance had a similar trend to the one measured, and therefore, we started to try to improve the model.

Besides, to refine on the precision of the model at neighborhood scale, three urban parameters were also added to the energy balance. The following steps describe the main phases for the definition of the model:

• Identification of the input data of the built environment. At first, data about the main characteristics of the built environment were used for each mesh together with the calculation of the geometric variables with GIS tool; then, the buildings were grouped for periods of construction, and therefore, at each group, the characteristics of those buildings have been associated with a weight equal to the percentage quota in volume; many attempts have been made to reduce model errors; for example, entering the maintenance level to reduce the thermal transmittance of the windows, but this evaluation did not lead to a significant improvement of the model;

• Introduction of the SVF to describe the solar exposition and the thermal radiation lost to the sky of the built environment;

• To take into account the paths of the sun (and to reduce errors), in the calculation of solar exposure, the MOS and the H/H_avg have been added;

• Comparison between the average climate data in the city of Turin and the data of the nearest WS to each mesh.

After identifying the main variables that affect energy consumption, the model was optimized to reduce errors. In this work, different types of errors were considered: the relative, the absolute relative, and the mean error were used to optimize the model comparing the measured and calculated values for each month and year. With the support of the iterative procedure on excel spreadsheets, the errors were reduced by introducing new data and urban variables. Since in almost all the meshes the share of residential buildings connected to the DHN is prevalent, a constant specific consumption has been assumed for non-residential buildings. For the industrial activity, only in three meshes, there are high percentages of this activity: 1350, 1403, and 1402; this area is the industrial zone called “Mirafiori.” From the analysis it has emerged that:

• 29 meshes have consumption related to residential users, with a high percentage of residential buildings of on average 76%;

• In the meshes 979, 1034, 1141, 1300, 1353, and 1405, there is a high percentage of municipal and commercial buildings; as already mentioned, the energy consumption for space heating of commercial buildings was considered constant with an annual specific consumption of 22–30 kWh/m³/y (Mutani and Todeschi 2017; Mutani et al. 2016);

• In the meshes 1350, 1402, and 1403, half of the buildings are residential and the other half industrial; mainly residential buildings are connected to the DHN and, for the remaining industrial portion (i.e., Mirafiori), a constant specific consumption was used.

Figures 6, 7, and 8 show some examples of the monthly consumptions for space heating and the domestic hot water profile with reference to the following meshes:

• 1350 (Fig. 6), for residential buildings built between 1946 and 1960;

• 1351 (Fig. 7), for residential buildings built between 1961 and 1970;

• 1296 (Fig. 8), for residential buildings built between 1971 and 1980.

Fig. 6

Monthly space heating and domestic hot water profile (MWh/month) for the August 2014–August 2015 period: comparison between the measured and the calculated consumptions for mesh “1350” in which the nearest WS “Politecnico” and the average weather data were used

Fig. 7

Monthly space heating and domestic hot water profile (MWh/month) for the June 2013–June 2014 period: comparison between the measured and the calculated consumptions for mesh “1351” in which the nearest WS “Politecnico” and the average weather data were used

Fig. 8

Monthly space heating and domestic hot water profile (MWh/month) for the July 2014–July 2015 period: comparison between the measured and the calculated consumptions for mesh “1296” in which the nearest WS “Politecnico” and the average weather data were used

In addition, the energy consumptions were compared considering the average weather data from five WSs in Turin (T_avg) and the weather data from the nearest WSs (T_ws). The results show that the air temperatures, T_ws, are slightly higher than the average air temperatures, T_avg, in Turin, and the results of the calculated energy consumptions in these cases are consequently higher. Finally, the data regarding domestic hot water use are quite constant in the spring/summer, but this energy consumption value depends on the number of buildings that have hot water systems connected to the DHN in each mesh.

The absolute relative errors (|E_r|) are reported in Fig. 9; the |E_r| was chosen to present the results because it is more significant and the difference between the monthly measured values and the calculated values add up because they are always positive. In this work, the absolute relative errors were considered not significant when the energy consumptions were low. In order to take into account any final balance adjustments of the effective energy consumptions made by the DH company, the global consumption was measured for the three heating seasons and compared with the result of the model (see Appendix 3).

Fig. 9

Absolute relative errors |Er| applying the energy balance models at a district scale: a H + DHW < 1960; b H + DHW 1961–70; c H + DHW 1971–90; d H for all periods

In general, |E_r| are variable between 4 and 17% but higher values (i.e., meshes 979, 1190, and 1402) can be observed when the number of building connected to the DHN is very low (DH % and number of buildings). Moreover, the meshes 1402 and 1403 have and high percentage of industrial buildings and then the accuracy of this model is lower. The E_r and |E_r| increased when the T_avg was used, although no significant differences were observed; in this case, the E_r,global was also limited.

The absolute relative errors of the model were georeferenced at a mesh scale, as shown in Fig. 10 a and b. As previously mentioned, there are no major error differences between the model with the average Turin air temperature data and the data from the nearest WS. These results, which have similar errors, are due to the fact that the analysis was made on large neighborhoods of 1 km² or maybe Turin is not a very large city. Consequently, there are no high variations in air temperature, due to the fact that the analyzed areas are all urbanized, and there are therefore limited microclimatic variations. If the errors are compared with the information in Figs. 6, 7, 8, and 9, higher |E_r| can be observed in meshes with:

• A low percentage of buildings connected to the DHN (meshes 1033, 1034, 1190, 1402);

• A low percentage of residential buildings (meshes 1141, 1034, and 1402); for example, there is a significant quota of municipal buildings in mesh 1141;

• High values of NDVI (more green areas) and/or high values of Albedo A_NIR (meshes 979, 1033, 1034, 1190);

• High BCR (meshes 1034, 1086, 1190, 1298, 1353, 1402);

• Low SVF_g (meshes 1033, 1034, 1141, 1244, 1297);

• Low values of H/H_avg (meshes 1033, 1034, 1141, 1190, 1402).

Fig. 10

a Absolute relative error with reference to the monthly energy balance model using data from the nearest WS. b Absolute relative error with reference to the monthly energy balance model using the average Turin data

Mesh 979 was considered as a particular case because it is the only mesh with the majority of buildings constructed during the 1981–1990 period. As not enough data were available for this construction period, it was not possible to optimize the model considering this period. However, further evaluations could be made with more data to understand whether and if so what other urban parameters affect the energy consumption of buildings built between 1981 and 1990.

Figure 11 refers to a comparison of the measured data (y-axis) with the calculated data (x-axis). The global consumptions (of three consecutive heating seasons) are indicated for each mesh, and the H + DHW group (Fig. 11a) is distinguished from the H group (Fig. 10b).

Fig. 11

The calculated energy consumption value on the x-axis were compared with the measured value on the y-axis: a the “H + DHW” group and b the “H” group

Some simulations were conducted to understand how the urban form influences the energy consumption of residential buildings. Using the variability of the data (Table 4), four scenarios were hypothesized considering different levels of solar exposition: (i) unfavorable low solar exposition, with an SVF of 0.34 and MOS of 0.35; two intermediate conditions, with (ii) an SVF of 0.34 and MOS of 0.56, and (iii) an SVF of 0.73 and MOS of 0.35 (iv) favorable conditions with high solar exposition, with an SVF of 0.73 and MOS of 0.56.

The results of scenarios (ii), (iii), and (iv) are compared in Fig. 12 with the most unfavorable scenario (i) for all the H and H + DHW groups. The results show that the energy consumptions with the more favorable conditions of solar exposition (scenario (iv)) decreased by 10.9% compared with the most unfavorable conditions (scenario (i)). These results are the average values of the 33 analyzed meshes. Two examples of meshes with buildings from different periods of construction are compared in Fig. 13 with different solar expositions. Again, in this case, the most unfavorable condition (scenario (i)) was compared with the more favorable solar expositions (scenarios (ii), (iii), and (iv)). The results show a number of differences: there were lower energy consumptions for the 1300 mesh with older buildings, and the energy consumptions could be reduced by as much as 10.1% with better solar conditions, while this difference was 8.4%.

Fig. 12

Comparison of the energy consumptions for different solar exposition scenarios: (i) SVF_g = 0.34 and MOS = 0.35; (ii) SVF_g = 0.73 and MOS = 0.35; (iii) SVF_g = 0.34 and MOS = 0.56; (iv) SVF_g = 0.73 and MOS = 0.56

Fig. 13

The energy consumption trends with the outdoor air temperature for two meshes with different construction periods and different solar expositions: mesh no. 1300 (1919–1945 period) and mesh no.1085 (1961–1970 period)

Conclusions

In this work, a simplified building-scale energy balance has been adapted to an urban scale by introducing a number of urban context variables calculated by means of a GIS. Therefore, a new model has been presented to estimate the monthly energy consumption of the residential buildings stock, which also considers the urban context as an energy-dependent variable. In order to adapt the energy balance to an urban scale and to investigate how the urban form can influence energy consumptions, a number of urban variables have been introduced. Solar exposition and heat exchanges with the external environment have been considered using the SVF, the H/H_avg, and the MOS.

The results of this first investigation show that the simplified, quasi-steady state heat balance can produce good results at an urban scale, especially for areas with old buildings, with absolute errors of only 4–17%. It is to note that such results will be optimized in future works, increasing the precision of the model. The methodology has been verified using the H and DHW energy consumption data for three consecutive heating seasons (2012/2013, 2013/2014, and 2014/2015) from thirty-three 1 km² meshes in the Turin urban context. In order to take into account the climatic and microclimatic conditions, energy consumptions have been compared, considering the average weather data of five WSs in Turin and the weather data that referred to the nearest WS. The results have confirmed that the energy consumptions in these areas also depend on the microclimate, with better results being obtained for the nearest WS: lower absolute relative errors were observed for the nearest WS, but higher errors were observed when the average weather conditions of the city were considered. Some simulations have been made, using the application field of the model, in which the SVF, H/H_avg, and MOS values were modified in the energy balance model. The obtained results confirm that solar exposure and heat exchanges with the external environment have a significant effect on energy consumptions. In particular, in favorable conditions (high SVF, H/H_avg, and MOS values), the energy consumption values were about 10% lower than the unfavorable condition values.

Some considerations can be drawn, from the BCR, A_NIR, and NDVI maps, about the influence of the microclimate on the energy consumptions of buildings. Warmer air temperatures have been observed in the central areas of Turin, which have high BCR and low A_NIR and NDVI. The monthly air temperature of the coldest months was about 1.5 °C higher in these areas than in the other areas, and the energy consumptions were therefore lower. These aspects will be analyzed in future work, where the UHI effect will also be considered.

This monthly model has significant implications for the understanding of how to identify effective energy retrofit measures, considering the more critical areas. Since the model is very flexible, it is also possible to apply it to other large urban contexts, in order to obtain a description of the energy situation, with monthly details. In addition, the results of these models should help to improve predictions of the impact of an urban context on the energy consumption of buildings, and to introduce a simple energy balance model for residential buildings at a neighborhood scale. Furthermore, one of the main objective of this model is to create a decision support system for citizens, designers, and energy policy makers. In particular, this model is purposely designed (i) to draw up new neighborhoods by optimizing energy performance of buildings according to urban characteristics, and (ii) to identify the most effective efficiency measure for the existing neighborhoods (e.g., thermal insulation of the roofs, walls, windows, and boiler substitution, by evaluating the RES potential according to energy consumption, building features, users, climate, and microclimate conditions).

To optimize the monthly engineering model presented, future developments of this research will introduce:

• New urban energy-related variables, such as the impact of shading on the building stock with a variable solar expositions during the year, the albedo characteristics of outdoor surfaces, and the presence of vegetation and water, which, as already mentioned, mitigate the microclimate.

• Some socio-economic variables that could be introduced to evaluate the inhabitants’ behavior and their attitude to energy-saving measures and to the use of RES technologies.

• The distribution losses in the DHN will be explored referring to existing grid models (Guelpa et al. 2018; Badami and Fambri 2019).

Furthermore, if the data on buildings built after 1980 were available, this engineering model can be updated for newer building stocks.

Appendices

Appendix 1

Table 5 provides information on the main characteristics of residential buildings analyzed in the districts connected to the DH network at a mesh scale. The following are indicated for each mesh: the number of buildings, the average height, the heated gross volume, the usable area, the occupancy, the average value of the S/V, the nearest WS with the HDD, the type of DH system (for H or for H + DHW), and the percentage of heated residential volumes connected to the DH

Table 5 The main characteristics of the residential buildings for each mesh: number of buildings

Tables 6 and 7 indicate the main input data that were used to create the energy balance model for groups 1 “H + DHW” and 2 “H”.

Table 6 Building characteristics of group 1 “H + DHW” at a mesh scale

Table 7 Building characteristics of group 2 “H” at a mesh scale

Appendix 2

To better understand the case study, some data and variables are mapped in Figs. 14, 15, 16, and 17. These figures show some of the urban variables and the energy performances for each mesh in the DH area of Turin. The color of the outline mesh specifies a homogeneous group of residential buildings, on the basis of the energy consumption types (H + DHW or H) and of the main period of construction. Figure 14 a describes the quota of residential buildings connected to the DHN (percentage value). The measured energy performances (kWh/m³/y using the gross heated volume) of the different meshes can be observed in Fig. 14 b for the 2014–2015 period. Figure 15 a and b show the values of the NDVI and the A_NIR of the outdoor surfaces that were calculated with the use of satellite images from November 2, 2015, at 10 a.m. Increasing values of NDVI and A_NIR may be observed from the center to the peripheral areas. Figs. 16 a and b and 17 a and b describe the urban morphology with the use of factors such as the BCR, the SVF_g, the MOS, and the H/H_avg.

Fig. 14

a Identification of homogenous groups considering the type of consumption, the main period of construction and the percentage of residential buildings connected to the DHN. b Distribution of the space heating and domestic hot water consumptions at a mesh scale for the 2014/15 period (Iren data)

Fig. 15

a Normalized difference vegetation index (NDVI). b Albedo near infrared (A_NIR) of the outdoor surface

Fig. 16

a Building coverage ratio (BCR). b Sky view factor (SVF_g)

Fig. 17

a Main orientation of the streets (MOS). b Relative height (H/H_avg)

Appendix 3

Table 8 provides information on the different relative errors comparing calculated and measured “H + DHW” and “H” consumptions (kWh/m³/y) for the three consecutive 2012/2013, 2013/2014, and 2014/15 heating seasons. It can be observed that E_r and |E_r| increased when the T_avg was used.

Table 8 Results of the application of the energy balance models at a neighborhood scale