Skip to main content
SpringerLink
Log in

Nonlocal and surface effects on the bending analysis of flexoelectrically actuated piezoelectric microbeams in hygrothermal environment

  • Published:
Sādhanā Aims and scope Submit manuscript

Abstract

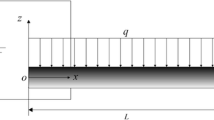
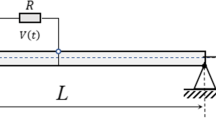
In this article, the bending analysis of flexoelectric functionally graded (FG) microbeams according to nonlocal elasticity theory is verified. To this end, higher order refined beam theory has been used. The foundation of FG microbeam includes Winkler-Pasternak layer. Hamilton’s principle is used to obtain the governing equations based on the nonlocal theory and solved employing an analytical solution. The model is designed in such a way that the properties change continuously. A parametric study is presented to inquire the nonlocal parameter, power-law hygro-thermal-loadings, flexoelectric effect, transverse external loading, on the bending characteristics of FG microbeam. It is found that boundary conditions, flexoelectric effect, nonlocal parameter, power-law index and beam geometrical parameters have notable effects on dimensionless deflection of FG microscale beams.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Figure 1
Figure 2
Figure 3
Figure 4
Figure 5
Figure 6
Figure 7
Figure 8
Figure 9
Figure 10
Figure 11
Figure 12

Similar content being viewed by others

References

  1. Eringen A 1968 Mechanics of micromorphic continua. In: Mechanics of Generalized Continua. Springer, Berlin, Heidelberg, pp 18–35

  2. Eringen A 1972 Nonlocal polar elastic continua. Int. J. Eng. Sci. 10: 1–16

    Article  MathSciNet  Google Scholar 

  3. Ansari R, Pourashraf T and Gholami R 2015 An exact solution for the nonlinear forced vibration of functionally graded nanobeams in thermal environment based on surface elasticity theory. Thin Walled Struct. 93: 169–176

    Article  Google Scholar 

  4. Kiani Y, Rezaei M, Taheri S, Eslami M R 2011 Thermo-electrical buckling of piezoelectric functionally graded material Timoshenko beams. Int. J. Mech. Mater. Des. 7: 185–197

    Article  Google Scholar 

  5. Rahmani O and Jandaghian A A 2015 Buckling analysis of functionally graded nanobeams based on a nonlocal third-order shear deformation theory. Appl. Phys. A. 119: 1019–1032

    Article  Google Scholar 

  6. Yang J, Ke L L and Kitipornchai S 2010 Nonlinear free vibration of single-walled carbon nanotubes using nonlocal Timoshenko beam theory. Physica E: Low-dimensional Systems and Nanostructures. 42: 1727–1735

    Article  Google Scholar 

  7. Ebrahimi F and Barati M R 2016 Dynamic modeling of a thermo–piezo-electrically actuated nanosize beam subjected to a magnetic field. Appl. Phys. A. 122: 1–18

    Google Scholar 

  8. Ebrahimi F and Barati M R 2016 Electromechanical buckling behavior of smart piezoelectrically actuated higher-order size-dependent graded nanoscale beams in thermal environment. Int. J. Smart Mater. Nano Struct. 7(2): 69–90

    Article  Google Scholar 

  9. Ebrahimi F and Barati M R 2016 An exact solution for buckling analysis of embedded piezoelectro-magnetically actuated nanoscale beams. Adv. Nano Res. 4(2): 65–84

    Article  Google Scholar 

  10. Ebrahimi F and Barati M R 2018 Vibration analysis of smart piezoelectrically actuated nanobeams subjected to magneto-electrical field in thermal environment. J. Vib. Control. 24(3): 549–564

    Article  MathSciNet  Google Scholar 

  11. Ebrahimi F and Barati M R 2017 Buckling analysis of nonlocal third-order shear deformable functionally graded piezoelectric nanobeams embedded in elastic medium. J. Braz. Soc. Mech. Sci. Eng. 39: 937–952

    Article  Google Scholar 

  12. Roque C M C, Ferreira A J M and Reddy J N 2011 Analysis of Timoshenko nanobeams with a nonlocal formulation and meshless method. Int. J. Eng. Sci. 49: 976–984

    Article  Google Scholar 

  13. Peddieson J, Buchanan G R and McNitt R P 2003 Application of nonlocal continuum models to nanotechnology. Int. J. Eng. Sci. 41: 305–312

    Article  Google Scholar 

  14. Civalek O and Demir C 2011 Bending analysis of microtubules using nonlocal Euler-Bernoulli beam theory. Appl. Math, Model. 35: 2053–2067

    Article  MathSciNet  Google Scholar 

  15. Wang Q 2005 Wave propagation in carbon nanotubes via nonlocal continuum mechanics. J. Appl. Phys. 98: 124301

    Article  Google Scholar 

  16. Wang C M, Kitipornchai S, Lim C W and Eisenberger M 2008 Beam bending solutions based on nonlocal Timoshenko beam theory. J. Eng. Mech. 134: 475–481

    Article  Google Scholar 

  17. Murmu T and Pradhan S C 2009 Buckling analysis of a single-walled carbon nanotube embedded in an elastic medium based on nonlocal elasticity and Timoshenko beam theory and using DQM. Physica E: Low-dimensional Systems and Nanostructures. 41: 1232–1239

    Article  Google Scholar 

  18. Arefi M and Zenkour A M 2016 A simplified shear and normal deformations nonlocal theory for bending of functionally graded piezomagnetic sandwich nanobeams in magneto-thermo-electric environment. J. Sandw. Struct. Mater. 18: 624–651

    Article  Google Scholar 

  19. Zenkour A M and Sobhy M 2013 Nonlocal elasticity theory for thermal buckling of nanoplates lying on Winkler-Pasternak elastic substrate medium. Physica E: Low-dimensional Systems and Nanostructures. 53: 251–259

    Article  Google Scholar 

  20. Ghorbanpour Arani A and Zamani M H 2019 Investigation of electric field effect on size-dependent bending analysis of functionally graded porous shear and normal deformable sandwich nanoplate on silica Aerogel foundation. J. Sandw. Struct. Mater. 21(8): 2700–2734

    Article  Google Scholar 

  21. Şimşek M and Yurtcu H H 2013 Analytical solutions for bending and buckling of functionally graded nanobeams based on the nonlocal Timoshenko beam theory. Compos. Struct. 97: 378–386

    Article  Google Scholar 

  22. Tornabene F 2009 Free vibration analysis of functionally graded conical, cylindrical shell and annular plate structures with a four-parameter power-law distribution. Comput Method Appl. Mech. Eng. 198: 2911–2935

    Article  Google Scholar 

  23. Zghal S, Frikha A and Dammak F 2018 Mechanical buckling analysis of functionally graded power-based and carbon nanotubes-reinforced composite plates and curved panels. Compos. Part B: Eng. 150: 165–183

    Article  Google Scholar 

  24. Tornabene F, Liverani A and Caligiana G 2011 FGM and laminated doubly curved shells and panels of revolution with a free-form meridian: a 2-D GDQ solution for free vibrations. Int. J. Mech. Sci. 53: 446–470

    Article  Google Scholar 

  25. Frikha A, Zghal S and Dammak F 2018 Dynamic analysis of functionally graded carbon nanotubes-reinforced plate and shell structures using a double directors finite shell element. Aerosp. Sci. Technol. 78: 438–451

    Article  Google Scholar 

  26. Tornabene F and Reddy J N 2013 FGM and laminated doubly-curved and degenerate shells resting on nonlinear elastic foundations: a GDQ solution for static analysis with a posteriori stress and strain recovery. J. Indian Inst. Sci. 93: 635–688

    MathSciNet  Google Scholar 

  27. Trabelsi S, Frikha A, Zghal S and andDammak F, 2019 A modified FSDT-based four nodes finite shell element for thermal buckling analysis of functionally graded plates and cylindrical shells. Eng. Struct. 178: 444–459

    Article  Google Scholar 

  28. Tornabene F, Fantuzzi N, Viola E and Batra R C 2015 Stress and strain recovery for functionally graded free-form and doubly-curved sandwich shells using higher-order equivalent single layer theory. Compos. Struct. 119: 67–89

    Article  Google Scholar 

  29. Tornabene F, Fantuzzi N, Bacciocchi M and Viola E 2016 Effect of agglomeration on the natural frequencies of functionally graded carbon nanotube-reinforced laminated composite doubly-curved shells. Compos. Part B: Eng. 89: 187–218

    Article  Google Scholar 

  30. Ebrahimi F and Salari E 2016 Effect of various thermal loadings on buckling and vibrational characteristics of nonlocal temperature-dependent FG nanobeams. Mech. Adv. Mater. Struct. 23: 1379–1397

    Article  Google Scholar 

  31. Sobhy M 2013 Buckling and free vibration of exponentially graded sandwich plates resting on elastic foundations under various boundary conditions. Compos. Struct. 99: 76–87

    Article  Google Scholar 

  32. Ebrahimi F and Salari E 2015 Thermo-mechanical vibration analysis of nonlocal temperature-dependent FG nanobeams with various boundary conditions. Compos. Part B: Eng. 78: 272–290

    Article  Google Scholar 

  33. Berrabah H M, Tounsi A, Semmah A and Adda B 2013 Comparison of various refined nonlocal beam theories for bending, vibration and buckling analysis of nanobeams. Struct. Eng. Mech. 48: 351–365

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Faculty of Engineering, Imam Khomeini International University, Qazvin, Iran

    Farzad Ebrahimi & Mahsa Karimiasl

  2. Department of Aerospace Engineering, Indian Institute of Science, Bangalore, India

    Vinyas Mahesh

Authors
  1. Farzad Ebrahimi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Mahsa Karimiasl
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Vinyas Mahesh
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Farzad Ebrahimi.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ebrahimi, F., Karimiasl, M. & Mahesh, V. Nonlocal and surface effects on the bending analysis of flexoelectrically actuated piezoelectric microbeams in hygrothermal environment. Sādhanā 46, 107 (2021). https://doi.org/10.1007/s12046-021-01625-0

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s12046-021-01625-0

Keywords

Search

Navigation