Measurement of productivity changes for general network production systems with stochastic data

Abstract

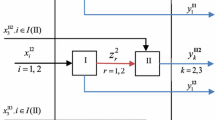
Performance evaluation of network production systems has been widely studied in recent Data Envelopment Analysis (DEA) literature where internal relations of sub-units are taken into consideration. Most of prior work assumes network systems to have simple series or parallel structures. Complexities of some practical production processes require development of DEA models for their effective analysis. However; input, intermediate products and/or output data are often stochastic and linked to exogenous random variables in most applications. The current study extends Malmquist Productivity Index (MPI) for investigating productivity changes of general network production units with stochastic data in a DEA framework. The proposed stochastic performance analysis models are then transformed into deterministic equivalent non-linear forms so they could be simplified to deterministic programming with quadratic constraints. Numerical examples including an application to productivity evaluation of branches of a university system are presented to illustrate the applicability of the proposed framework.

Appendix A

To convert the chance-constrained optimization Model (4) to associate deterministic equivalent Model (5), we can proceed as follows. Note that the same argument could be presented for introducing Model (7). Here, $\Pr$ means ‘Probability’ and $\alpha$ is a predetermined value between 0 and 1.

The first constraint of Model (4) can be stated as follows:

$$ \Pr \left\{ {\sum\limits_{{p \in P_{I} (i)}} {\sum\limits_{j = 1}^{n} {\lambda_{j}^{p} (\tilde{x}_{ij}^{p} )^{l} \le \theta (\tilde{x}_{ik} )^{f} } } } \right\} \ge 1 - \alpha ,\quad i = 1, \ldots ,m $$

By considering external slack value $s_{i}$, we have:

$$ \Pr \left\{ {\sum\limits_{{p \in P_{I} (i)}} {\sum\limits_{j = 1}^{n} {\lambda_{j}^{p} (\tilde{x}_{ij}^{p} )^{l} - \theta (\tilde{x}_{ik} )^{f} \le 0} } } \right\} = (1 - \alpha ) + s_{i} ,\quad i = 1, \ldots ,m $$

So, there exist a positive slack variable $s_{i} > 0$ such that the above relation take this form:

$$ \Pr \left\{ {\sum\limits_{{p \in P_{I} (i)}} {\sum\limits_{j = 1}^{n} {\lambda_{j}^{p} (\tilde{x}_{ij}^{p} )^{l} - \theta (\tilde{x}_{ik} )^{f} \le s_{i} } } } \right\} = 1 - \alpha ,\quad i = 1, \ldots ,m $$

Accordingly, by using the definition of expected value and variance of the elements, we may write the above equation as follows:

$$ \Pr \left[ {\frac{{\sum\limits_{{p \in P_{I} (i)}} {\sum\limits_{j = 1}^{n} {\lambda_{j}^{p} (\tilde{x}_{ij}^{p} )^{l} - \theta (\tilde{x}_{ik} )^{f} } } - E\left( {\sum\limits_{{p \in P_{I} (i)}} {\sum\limits_{j = 1}^{n} {\lambda_{j}^{p} (\tilde{x}_{ij}^{p} )^{l} - \theta (\tilde{x}_{ik} )^{f} } } } \right)}}{{\sqrt {var\left( {\sum\limits_{{p \in P_{I} (i)}} {\sum\limits_{j = 1}^{n} {\lambda_{j}^{p} (\tilde{x}_{ij}^{p} )^{l} - \theta (\tilde{x}_{ik} )^{f} } } } \right)} }} \ge \frac{{s_{i} - E\left( {\sum\limits_{{p \in P_{I} (i)}} {\sum\limits_{j = 1}^{n} {\lambda_{j}^{p} (\tilde{x}_{ij}^{p} )^{l} - \theta (\tilde{x}_{ik} )^{f} } } } \right)}}{{\sqrt {var\left( {\sum\limits_{{p \in P_{I} (i)}} {\sum\limits_{j = 1}^{n} {\lambda_{j}^{p} (\tilde{x}_{ij}^{p} )^{l} - \theta (\tilde{x}_{ik} )^{f} } } } \right)} }}} \right] = \alpha . $$

For the sake of simplicity let denote $\sqrt {var\left( {\sum\limits_{{p \in P_{I} (i)}} {\sum\limits_{j = 1}^{n} {\lambda_{j}^{p} (\tilde{x}_{ij}^{p} )^{l} - \theta (\tilde{x}_{ik} )^{f} } } } \right)}$by$\sigma_{i} \left( {\theta ,\lambda } \right)$. Therefore, we have:

$$ \Pr \left[ {\frac{{\sum\limits_{{p \in P_{I} (i)}} {\sum\limits_{j = 1}^{n} {\lambda_{j}^{p} (\tilde{x}_{ij}^{p} )^{l} - \theta (\tilde{x}_{ik} )^{f} } } - \sum\limits_{{p \in P_{I} (i)}} {\sum\limits_{j = 1}^{n} {\lambda_{j}^{p} (x_{ij}^{p} )^{l} + \theta (x_{ik} )^{f} } } }}{{\sigma_{i} \left( {\theta ,\lambda } \right)}} \ge \frac{{s_{i} - \sum\limits_{{p \in P_{I} (i)}} {\sum\limits_{j = 1}^{n} {\lambda_{j}^{p} (x_{ij}^{p} )^{l} + \theta (x_{ik} )^{f} } } }}{{\sigma_{i} \left( {\theta ,\lambda } \right)}}} \right] = \alpha $$

By denoting the left-hand side of the above inequality by $z_{j},$ it follows a normal standard distribution with zero mean and unit variance. Hence, we can write:

$\Pr \left[ {z_{j} \ge \frac{{s_{i} - \sum\limits_{{p \in P_{I} (i)}} {\sum\limits_{j = 1}^{n} {\lambda_{j}^{p} (x_{ij}^{p} )^{l} + \theta (x_{ik} )^{f} } } }}{{\sigma_{i} \left( {\theta ,\lambda } \right)}}} \right] = \alpha.$ Thus, we have $\varPhi \left[ {\frac{{ - s_{i} + \sum\limits_{{p \in P_{I} (i)}} {\sum\limits_{j = 1}^{n} {\lambda_{j}^{p} (x_{ij}^{p} )^{l} - \theta (x_{ik} )^{f} } } }}{{\sigma_{i} \left( {\theta ,\lambda } \right)}}} \right] = \alpha,$ where $\varPhi$ represent the normal cumulative distribution function. So, taking the inverse, we obtain $\left[ {\frac{{ - s_{i} + \sum\limits_{{p \in P_{I} (i)}} {\sum\limits_{j = 1}^{n} {\lambda_{j}^{p} (x_{ij}^{p} )^{l} - \theta (x_{ik} )^{f} } } }}{{\sigma_{i} \left( {\theta ,\lambda } \right)}}} \right] = \varPhi^{ - 1} (\alpha ),$ which could be stated as $- s_{i} + \sum\limits_{{p \in P_{I} (i)}} {\sum\limits_{j = 1}^{n} {\lambda_{j}^{p} (x_{ij}^{p} )^{l} - \theta (x_{ik} )^{f} } } = \varPhi^{ - 1} (\alpha )\sigma_{i} \left( {\theta ,\lambda } \right)$or equivalently as follows:

$\sum\limits_{{p \in P_{I} (i)}} {\sum\limits_{j = 1}^{n} {\left( {\lambda_{j}^{p} (x_{ij}^{p} )^{l} } \right) - \varPhi^{ - 1} (\alpha )\sigma_{i} \left( {\theta ,\lambda } \right) \le \theta (x_{ik} )^{f} ,} } \quad i = 1, \ldots ,m.$ This is the first constraint of the model (5). The other constraints could be achieved in the same way.

For calculating $\left( {\sigma_{i} \left( {\theta ,\lambda } \right)} \right)^{2}$ we can write:

$$ \begin{aligned} & \text{var}\left( {\sum\limits_{{p \in P_{I} (i)}} {\sum\limits_{j = 1}^{n} {\lambda_{j}^{p} (\tilde{x}_{ij}^{p} )^{l} - \theta (\tilde{x}_{ik} )^{f} } } } \right) = \text{var}\left( {\sum\limits_{{p \in P_{I} (i)}} {\sum\limits_{\begin{subarray}{l} j = 1 \\ j \ne o \end{subarray} }^{n} {\lambda_{j}^{p} (x_{ij}^{p} )^{l} + (\lambda_{j}^{p} - \theta )(x_{ik} )^{f} } } } \right) \\ & = \text{var}\left( {\sum\limits_{{p \in P_{I} (i)}} {\sum\limits_{\begin{subarray}{l} j = 1 \\ j \ne o \end{subarray} }^{n} {\lambda_{j}^{p} (x_{ij}^{p} )^{l} } } } \right) + \text{var}\left( {(\lambda_{j}^{p} - \theta )(x_{ik} )^{f} } \right) + 2\text{Cov}\left( {\sum\limits_{{p \in P_{I} (i)}} {\sum\limits_{\begin{subarray}{l} j = 1 \\ j \ne o \end{subarray} }^{n} {\lambda_{j}^{p} (x_{ij}^{p} )^{l} } } ,(\lambda_{j}^{p} - \theta )(x_{ik} )^{f} } \right) \\ \end{aligned} $$

Therefore,

$$ \begin{aligned} \left( {\sigma_{i} \left( {\theta ,\lambda } \right)} \right)^{2} = \sum\limits_{{p \in P_{I} (i)}} {\sum\limits_{\begin{subarray}{l} j = 1 \\ j \ne k \end{subarray} }^{n} {((\lambda_{j}^{p} )^{2} Var(\tilde{x}_{ij}^{p} )^{l} ) + \sum\limits_{o \ne k} {\sum\limits_{j \ne k} {\lambda_{o}^{p} \lambda_{j}^{p} Cov(\tilde{x}_{io}^{p} ,\tilde{x}_{ij}^{p} )} } } \,\,\,\,} \hfill \\ + 2(\lambda_{k}^{p} - \theta )\sum\limits_{o \ne k} {\lambda_{k}^{p} Cov(\tilde{x}_{io}^{p} ,\tilde{x}_{ik}^{p} )} + (\lambda_{k}^{p} - \theta )^{2} Var(\tilde{x}_{ik}^{p} )^{f} \hfill \\ \end{aligned} $$

In the model (5), $\left( {\sigma_{i} \left( {\theta ,\lambda } \right)} \right)^{2}$ is denoted by non-negative variables $(\omega_{i}^{l} )^{2}$.