Surface waves in a cylindrical borehole through partially-saturated porous solid

Abstract

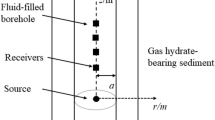
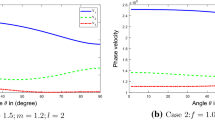
Propagation of surface waves is discussed in a cylindrical borehole through a liquid-saturated porous solid of infinite extent. The porous medium is assumed to be a continuum consisting of a solid skeletal with connected void space occupied by a mixture of two immiscible inviscid fluids. This model also represents the partial saturation when liquid fills only a part of the pore space and gas bubbles span the remaining void space. In this isotropic medium, potential functions identify the existence of three dilatational waves coupled with a shear wave. For propagation of plane harmonic waves along the axially-symmetric borehole, these potentials decay into the porous medium. Boundary conditions are chosen to disallow the discharge of liquid into the borehole through its impervious porous walls. A dispersion equation is derived for the propagation of surface waves along the curved walls of no-liquid (all gas) borehole. A numerical example is studied to explore the existence of cylindrical waves in a particular model of the porous sandstone. True surface waves do not propagate along the walls of borehole when the supporting medium is partially saturated. Such waves propagate only beyond a certain frequency when the medium is fully-saturated porous or an elastic one. Dispersion in the velocity of pseudo surface waves is analysed through the changes in consolidation, saturation degree, capillary pressure or porosity.

Appendix

In terms of measurable quantities, elastic constants in three-phase porous solid are given by

$$\begin{aligned} a_{11}= & {} K_p,\\\ a_{12}= & {} a_{21}=K_{g}\delta _{s}(1-\sigma )(K_c+K_{l})/ K,\\\ a_{13}= & {} a_{31}=K_{l}\delta _{s}\sigma (K_c+K_{g})/K,\\\ a_{22}= & {} K_{g}\delta _{g}[(1-\sigma )K_{l}+K_c]/K,\\\ a_{23}= & {} a_{32}=K_{g}K_{l}(1-\sigma )\delta _{l}/K,\\\ a_{33}= & {} K_{l}\delta _{l}(K_{g}\sigma +K_c)/K,\\ K= & {} K_{g}\sigma +K_c+K_{l}(1-\sigma ),\\\ K_c= & {} \chi \sigma (1-\sigma )K_g \end{aligned}$$

where $K_p,~K_{g}$ and $K_{l}$ are the bulk moduli of porous frame, gas and liquid phases respectively. The two pore-fluids are assumed immiscible. For miscible pore-fluids, constitutive relations involve Henry’s constant (Garg and Nayfeh 1986). As a result, the elastic coefficients $a_{ij}$ in relations (2–4) cease to be symmetric (i.e., $a_{ij}\ne a_{ji}$). The saturation degree $\sigma \in (0,~1)$ measures the share of liquid in filling the pores. $K_c$ is the equivalent bulk modulus (Garg and Nayfeh 1986) for macroscopic capillary pressure between wetting and non-wetting fluids. For partial saturation (i.e., $0<\sigma <1$), a capillary parameter ($\chi$) is used to fix the value of $K_c$ relative to the $K_g$.

Following Sharma (2012), three dilatational ($P_1,~P_2,~P_3$) waves and a shear (S) wave propagate in a three phase non-dissipative porous solid. The velocities ($\alpha _1>\alpha _2>\alpha _3$) of three dilatational waves are derived from the roots of a cubic equation in $\alpha ^2$, given by

$$\begin{aligned} D\alpha ^6-C\alpha ^4+B\alpha ^2-A=0. \end{aligned}$$

Coefficients in this cubic equation are defined as follows.

$$\begin{aligned}&\displaystyle A=\left( a_{11}+{4\over 3}G_p\right) A_1+a_{12}A_2+a_{13}A_3,\\&\displaystyle B=\left( a_{11}+{4\over 3}G_p\right) B_1-a_{12}B_2-a_{13}B_3+\delta _s\rho _{s}A_1,\\&\displaystyle C=\left( a_{11}+{4\over 3}G_p\right) C_1+\delta _s\rho _{s}B_1, ~~~D=\delta _s\rho _{s}C_1, \end{aligned}$$

where,

$$\begin{aligned} A_1= & {} a_{22}a_{33}-a_{23}a_{23},\\ A_2= & {} a_{23}a_{13}-a_{12}a_{33},\\ A_3= & {} a_{12}a_{23}-a_{13}a_{22},\\ B_1= & {} a_{22}\delta _l\rho _{l}+a_{33}\delta _g\rho _{g},\\ B_2= & {} a_{12}\delta _l\rho _{l},\\ B_3= & {} a_{13}\delta _g\rho _{g},\\ C_1= & {} \delta _g\rho _{g}\delta _l\rho _{l}. \end{aligned}$$

The velocity of lone shear wave in porous solid is given by $\beta =\sqrt{G_p/\delta _s\rho _s}$.

The coefficients for fluid–solid coupling in (10–11) are given by

$$\begin{aligned} \mu _{j}= & {} \frac{A_2-B_2\alpha _{j}^{2}}{A_1-B_1\alpha _{j}^{2}+C_1\alpha _{j}^{4}},\\ \nu _{j}= & {} \frac{A_3-B_3\alpha _{j}^{2}}{A_1-B_1\alpha _{j}^{2}+C_1\alpha _{j}^{4}},~(j=1,2,3). \end{aligned}$$