Conceptual design and virtual prototyping of a wearable upper limb exoskeleton for assisted operations

Abstract

This paper introduces a novel upper limb robotic exoskeleton designed to assist industrial operators in a wide range of manual repetitive tasks, such as tool handling and lifting/moving of heavy items. Due to its reduced size and high maneuverability, the proposed portable device may also be employed for rehabilitation purposes (e.g. as an aid for people with permanent neuromuscular diseases or post-stroke patients). Its primary function is to compensate the gravity loads acting on the human shoulder by means of a hybrid system consisting of four electric motors and three passive springs. The paper focuses on the exoskeleton mechanical design and virtual prototyping. After a preliminary review of the existent architectures and procedures aimed at defining the exoskeleton functional requirements, a detailed behavioral analysis is conducted using analytical and numerical approaches. The developed interactive model allows to simulate both kinematics and statics of the exoskeleton for every possible movement within the design workspace. To validate the model, the results have been compared with the ones achieved with a commercial multibody software for three different operator’s movements.

1 Introduction

In recent years, the interest for assistive devices has been increasing due to their proven effectiveness in many cardinal areas, such as medical treatments [1,2,3,4] and industrial manufacturing processes [5,6,7,8]. These advanced mechanical/mechatronic systems are gradually stepping from the research labs to the real life applications, mainly for the rehabilitation of injured or disabled patients [9, 10], but also for enhancing the operators performance in many work environments [11]. Under the trend of Industry 4.0 [12,13,14], the level of automation is constantly increasing in the production lines, though many manual repetitive tasks (e.g. tool handling, time-consuming overhead operations, machine loading/unloading, lifting/carrying of heavy components, operations under asymmetric un-ergonomic body postures, etc.), which cannot be automated, are still existent at large scale [15, 16]. They become arduous, exhausting or even dangerous after a certain amount of time. In fact, workers exposed to these activities are more likely to manifest work-related musculoskeletal disorders [17, 18].

Fig. 1

Examples of assistive devices for manual tasks in the manufacturing industry. From the left: the Mate [19], the AirFrame [20], the ShoulderX [21], the LegX [22] and the Laevo V2 [23]

Within this scenario, the development of portable, light-weight and ergonomic assistive devices seems to be an effective strategy to reduce the risk of injuries in manual manufacturing and also to avoid loss of productivity [5]. Their primary function is to assist people during the execution of specific movements by providing supplementary strength, making it possible, for instance, to deal with greater loads, to compensate for a lack of muscularity and to prevent from excessive fatigue. Wearable assistive devices, usually referred to as exoskeletons, are commonly designed to operate along their human counterparts, namely the lower/upper limbs or the neck area, though in the last case, if no particular functionalities are provided, the device could be better identified as a brace [24]. Ready examples of commercially available exoskeletons are the Mate, [19], the AirFrame [20] and the ShoulderX [21] for the upper limbs, the LegX [22] and the Hercule [25] for the lower limbs, and the Laevo V2 [23] for the lumbar region. Despite these promising solutions, shown in Fig. 1, have not yet been fully integrated in the industrial sector, many pilot studies highlighted their positive effects on the operators, which are well documented in [5, 8, 11, 26, 27]. Similarly, also soft exoskeletons (e.g. arm/leg exosuits [28, 29]) represent an important research topic, with several prototypes currently transitioning from lab to market. In this case, the system shall comprise deformable sensory-motor technologies, such as soft/compliant [30, 31] and sensors [32]).

Generally, the design of an efficient exoskeleton is a challenging task since it requires a deep knowledge of the biomechanics of human movements, which are often not simple and may involve many joints and parts [33]. From a kinematic standpoint, an exoskeleton must be quasi-equivalent to the related human limb, otherwise undesired motion and force contributes would be introduced during the functioning and then transmitted to the wearer, causing discomfort or even diseases [34]. These design issues are emphasized when considering the human upper limbs, because they are smaller than the lower limbs and they have mobility in a wide range of space, as clearly described in [35]. In particular, it shall be remarked that the shoulder is one of the most anatomically intricate region of the human body, as it combines four joints (i.e. the Glenohumeral joint, the Acromioclavicular joint, the Sternoclavicular joint and the Scapulothoracic joint, as shown in Fig. 2) and a large number of bones, muscles, ligaments and tendons [36]. Also, because of the intrinsic flexibility of the human musculoskeletal system, which varies between individuals based on their age, sex and state of health, a general parametric kinematic model cannot be easily formulated for the shoulder complex. Starting from [37], where the shoulder is simplified to a ball and socket joint, plenty of kinematic configurations have been proposed and analyzed. Most of these utilize serial chain manipulators and adopt a 3 Degrees of Freedom (DoFs) design for the Glenohumeral joint, where the axes of the 3 Revolute (R) joints must intersect the human shoulder center of rotation [3, 4, 38,39,40,41,42]. Other configurations employ 4R [43, 44] or 5R [34] redundant schematics with the aim of overcoming possible singular configurations. Alternative mechanical layouts can be found in [45], in [46], and in [47], where a double parallelogram linkage, a hyper-redundant chain and a scissors linkage are respectively proposed. Given that the exoskeleton is attached to the human arm and must resemble its motion, a standard design rule is to add extra DoFs in order to better follow the human shoulder’s broad variety of activities and avoid misalignment between human joints and exoskeleton joints. For a comprehensive review of the existent hardware in the field of upper limb exoskeletons, the interested reader may refer to [48,49,50].

Fig. 2

Biomechanics of the human shoulder

Fig. 3

Typical movements of the human upper limbs [51]

Besides the mechanism topology, another crucial point for the exoskeleton design is the selection of the balancing principle. According to the literature, the exoskeletons can be classified into active or passive types based on the presence or not of externally-powered actuators in the assisted mechanism [48]. The former provide reactive and precise assistance via the combined use of a sensory apparatus, a set of motors and a controller, whereas the latter rely on the presence of passive spring-like components to counterbalance the loads due to gravity. At the early design stage, the proper selection between them should be guided by the following points:

• Biomechanics of the human limb—A single DoF kinematic chain, such as the elbow joint, can adopt either active [52] or passive [53] balancing without any restriction. Obviously, in case of active balancing, the motor placement is to be carefully investigated in order to increase the overall compactness and ensure a sufficient level of mobility. Instead, when considering more complex scenarios, namely human limbs whose motions are unquestionably to be obtained by means of multi-DoFs chains (e.g. the shoulder joint), the designer may encounter issues in terms of maneuverability if an active balancing system is chosen because of the presence of many additional components installed therewith. A partial solution for this problem is the use of a remote actuation and cable-driven transmissions [50, 54, 55]. In any case, the overall assembly would be surely simplified if a passive system is implemented, as in [4].

• Balancing action—This aspect is strictly related to the field of application. As previously mentioned, the exoskeletons have potentials to be utilized in many situations, among which the assistance of workers that face repetitive tasks, but also the rehabilitation of stroke patients or the treatment of people with neuromuscular disorders. Therefore, on the basis of the specific assistance being provided, the exoskeleton balancing is expected to be more in static or dynamic conditions. Slow movements fall into the static balancing and leave the designer free to select either active or passive systems, whereas rapid movements are most likely to be assisted via a motorized solution. For industrial-oriented exoskeletons, an interesting study showing the priority joints for active assistance to prevent back and shoulder injuries can be found in [56].

• Balancing accuracy—While passive exoskeleton are usually constrained to a specific set of target tasks, the active balancing can be achieved for a broad range of movements by means of the sensory feedback and a rapid control action [57].

• Overall weight—As it may be expected, large and heavy linkages may need the use of motors to receive an adequate assistance. This is the case of heavy rehabilitation prototypes, as the ones visible in [3, 37]. Conversely, the passive balancing is promoted when light-weight and compact designs are required.

By combining these features, one could also synthesize hybrid exoskeletons, namely systems comprising both motorized joints and passive elastic elements [58]. These solutions allow to select smaller actuators, reducing the risk of collision between the components and facilitating the interaction with the wearer.

Fig. 4

Proof-of-concept design of the exoskeleton. a Example of the right-arm version on a manikin. b Detailed view of the main components. c Exploded CAD view. d Kinematic model and its DoFs

In this context, this paper aims to propose a novel portable, hybrid, interactive, upper limb exoskeleton to be used in both industrial and healthcare environments to reduce the human musculoskeletal loads. The idea is to combine the advances, in terms of mechanism efficiency, visible in recent academic research prototypes, with the benefits of the existent commercially available exoskeletons (such as the ones in Fig. 1), which can be outlined into simplified assembly, reduced weight and limited production costs. Therefore, the proposed exoskeleton makes use of a limited number of parts, which leads to a relatively simple structure. It follows the natural motions of the human shoulder (including the contributes from the shoulder girdle) and the elbow joints, i.e. the ones visible in Fig. 3. The balancing is achieved via the concurrent action of four electric DC motors and three linear springs placed between the rigid links. The paper focuses on the mechanical design of the device and describes its main characteristics. The exoskeleton kinematics and statics are considered in details. In particular, an analytical model is developed with the aim of determining the overall range of motion as well as the correct size of the motors and of the springs. Also, this parametric and efficient interactive model will surely be of interest for the controller design of the exoskeleton. As a last step, the model is validated through a commercial Multibody Dynamics (MBD) software under different working conditions.

The rest of the paper is structured as follows: Sect. 2 describes the main features of the proposed exoskeleton design, Sect. 3 recalls the background theory of planar balancers, Sect. 4 reports the developed analytical model and its numerical validation, whereas Sect. 5 provides the concluding remarks.

2 Design concept

Fig. 5

Exoskeleton primary motions. Single effect of $R_0$ (a), $R_1$ (b), $R_2$ (c), $R_3$ (d), $R_4$ (e) and $R_5$ (f)

For the design of the exoskeleton system, a number of features have been considered. First, in view of its use as a multi-tasking portable device, the compactness as well as the total weight and the user safety become primary concerns [59]. Second, the device must achieve high dexterity so as not to cause impediments to the user. This applies especially to the industrial devices (see Fig. 2), because rehabilitative devices usually need a smaller mobility and their design is focused on the motion accuracy. The embodiment design of the developed exoskeleton is described hereinafter. In particular, Fig. 4a shows the right-arm configuration of the portable device mounted on a manikin, whereas Fig. 4b and c provide a detailed view of its main components. As visible in these figures, the overall structure is compact and is connected to the human arm by means of two cuffs (i.e. Arm Holder and Forearm Holder). The kinematic model is depicted in Fig. 4d, where a simplified version of the overall exoskeleton is schematized. Differently from industrial solutions employing simplified kinematic chains (see, e.g., [19, 20]), the proposed mechanism has 6 DoFs for supporting the motion of the human shoulder and the elbow joints. With reference to Fig. 3, 2 R joints ($R_0$ and $R_1$ in Fig. 4d) are used to model the shoulder girdle movements, 3 R joints ($R_2$, $R_3$ and $R_4$ in Fig. 4d) provide the glenohumeral movements, and the last R joint ($R_5$ in Fig. 4d) is aligned with the elbow joint. Two parallelogram decoupling systems (Fig. 4c) have been included in the kinematic chain, making it possible to simplify the passive balancing [60], as it will be explained in the next section. Similar solutions can be found in [3, 42]. The basic motions of the exoskeleton, obtained by rotating a single R joint (from $R_0$ to $R_5$) while keeping the others fixed, are illustrated in Fig. 5. As visible in Figs. 5a and b, the exoskeleton can capture the glenohumeral joint deviations (displacement from S to $S^{'}$) in case of scapular abduction/adduction and shoulder girdle elevation/depression, which is a desirable quality, as clearly remarked in [61]. Naturally, to ensure a safety interaction with the operator, mechanical stoppers are implemented to limit the operative range of each R joint.

As for he gravity balancing, this is obtained by combining:

• Four electric motors, placed in $R_2$, $R_3$, $R_4$ and $R_5$. Among the available products on the market, the FLA-series of brushless DC motors (by Harmonic Drive SE), equipped with harmonic drive reducers, are here chosen mainly for their small size and high delivered torque. Clearly, the final selection from the manufacturer’s catalogs depends on the required torque, which in turn depends on the subject (and task) being assisted.

• Three Non-Zero Free Length (NZFL) linear springs, arranged between Link 0 and Link 1, Link 3 and Link 4, Auxiliary Link and Link 5. Ideally speaking, the Zero Free Length (ZFL) springs are preferable due to their simplified modeling and synthesis. However, they are not readily available and their practical realization requires the use of a wire-and-pulley mechanism [62], that is why many researches utilize NZFL springs [42].

Starting from the background theory, the above discussed points will be analyzed throughout the next sections.

3 Background on passive balancers

This section briefly summarizes the main results of previous studies in the field of passive balancers and extrapolates simple formulas that can help the designers in the synthesis process.

3.1 1 DoF balancer

The 1 DoF balancer [63] has been utilized as a basic module in many researches [64,65,66]. With reference to Fig. 6a, assuming that the link has null density, the torque produced by the mass placed at distance a from the ideal R joint, under the effect of gravity, is equal to:

$$\begin{aligned} M=mga\sin {\theta } \end{aligned}$$

(1)

Fig. 6

Planar 1 DoF balancer. a Gravity load acting on the system. b Balancing with a linear spring. c Balancing with a compliant spline beam

Fig. 7

Planar 2 DoF balancer. a Classic 2 links mechanism. b Decoupling mechanism. c Static analysis of the decoupling mechanism with external gravity forces. d Balancing with 2 linear springs

where $\theta$ represents the angular position of the link. By attaching an ideal ZFL linear spring between the ground and the link through two R joints, respectively at distance c and b from the principal R joint, as in Fig. 6b, the new moment equilibrium is as follows:

$$\begin{aligned} mga\sin {\theta }-kdb\sin {\alpha }=0 \end{aligned}$$

(2)

From the triangle of sides bcd, the following trigonometric correlation can be defined:

$$\begin{aligned} c\sin {\theta }=d\sin {\alpha } \;\; \rightarrow \;\;d=\frac{c\sin {\theta }}{\sin {\alpha }} \end{aligned}$$

(3)

By substituting Eqs. 3 in 2, the angles are elided and the expression of the spring stiffness becomes:

$$\begin{aligned} k=\frac{mga}{bc} \end{aligned}$$

(4)

or, if $a=b$:

$$\begin{aligned} k=\frac{mg}{c} \end{aligned}$$

(5)

Since the ZFL condition has practical limits, in the following two more solutions are discussed. The first considers spring with NZFL [67]. In this case, by assuming $d_0$ as the initial spring length, Eq. 2 can be rewritten as:

$$\begin{aligned} mga\sin {\theta }-k(d-d_0)b\sin {\alpha }=0 \end{aligned}$$

(6)

Then, by introducing Eq. 3, a new expression for k can be derived, i.e.:

$$\begin{aligned} k=\frac{mga}{bc\left( 1-\frac{d_0}{d}\right) } \end{aligned}$$

(7)

where $d=\sqrt{b^2+c^2-2bc\cos \theta }$ from the cosine theorem. To remove the dependence on $\theta$, one may consider $d=\sqrt{b^2+c^2}$, though this is valid if $\left| \frac{2bc}{b^2+c^2} \right| \le 1$. Under this condition, the spring stiffness becomes:

$$\begin{aligned} k=\frac{mga}{bc\left( 1-\frac{d_0}{\sqrt{b^2+c^2}}\right) } \end{aligned}$$

(8)

Note that for $d_0=0$, Eq. 8 coincides with Eq. 4. Quoting [53, 60], another possible way to reach the gravity balancing is the use of properly designed compliant mechanisms [68]. For instance, Fig. 6c shows a possible configuration of compliant balancer, namely a flexible beam whose shape is to be optimized in order to match a specific, pre-defined, force-deflection behavior ($F_b=F_b(\theta )$) in the angular range of interest [69,70,71].

3.2 2 DoFs balancer with decoupled architecture

For a 2 DoFs linkage, as the one depicted in Fig. 7a, an additional spring element (or, alternatively, a compliant mechanism) is needed. The torques due to gravity are given by:

$$\begin{aligned} M_1&=m_1ga_1\sin \theta _1+m_2g(l_1\sin \theta _1\nonumber \\&\quad -a_2\sin (\theta _1+\theta _2))=\nonumber \\&=m_1ga_1\sin \theta _1+m_2gl_1\sin \theta _1+M_2 \end{aligned}$$

(9)

$$\begin{aligned} M_2&=-m_2ga_2\sin (\theta _1+\theta _2) \end{aligned}$$

(10)

As it can be noted from Eqs. 9 and 10, both $M_1$ and $M_2$ are functions of $\theta _1$ and $\theta _2$, making it problematic to compensate the first/second R joint (see Fig. 7a) without taking into consideration the position of the other. To overcome this issue, two additional links (Auxiliary Links in Fig. 7b) can be added to form a parallelogram decoupling mechanism [60]. The direct advantages of such decoupling architecture can be deduced from the static analysis of Fig. 7c. In particular, Eq. 9 can be reformulated as:

$$\begin{aligned} M_{2,dec}=m_2ga_2\sin \theta _{2'} \end{aligned}$$

(11)

The rotational equilibrium of the auxiliary links gives:

$$\begin{aligned} R_{v2}l_1\sin \theta _1=R_{h2}l_1\cos \theta _1 \;\; \rightarrow \;\; R_{v2}=R_{h2}\frac{\cos \theta _1}{\sin \theta _1} \end{aligned}$$

(12)

and

$$\begin{aligned} M_{2,dec}=eR_{h2} \;\; \rightarrow \;\; R_{h2}= \frac{M_{2,dec}}{e} \end{aligned}$$

(13)

By knowing that $R_{v3}=m_2g$ and by considering Eqs. 12 and 13, the vertical equilibrium of the second auxiliary link becomes:

$$\begin{aligned} R_{v1}-m_1g=m_2g+\frac{M_{2,dec}}{e}\frac{\cos \theta _1}{\sin \theta _1} \end{aligned}$$

(14)

Now, being $R_{h1}=R_{h2}$, the expression of $M_{1,dec}$ can be derived as follows:

$$\begin{aligned} M_{1,dec}&=m_1ga_1\sin \theta _1+\left( m_2g+\frac{M_{2,dec}}{e}\frac{\cos \theta _1}{\sin \theta _1} \right) l_1\sin \theta _1\nonumber \\&-\frac{M_{2,dec}}{e}l_1\cos \theta _1\nonumber \\&=m_1ga_1\sin \theta _1+m_2gl_1\sin \theta _1 \end{aligned}$$

(15)

The effectiveness of the decoupling mechanism can be verified with a rapid comparison between Eqs. 9–10 and Eqs. 11–15. In case of NZFL springs (Fig. 7d), the stiffness constants are determined through the following formulas (obtained by reiterating the steps from Eqs. 2 to 8 with the new expressions of $M_{1,dec}$ and $M_{2,dec}$):

$$\begin{aligned} k_1&=\frac{m_1ga_1+m_2gl_1}{b_1c_1\left( 1-\frac{d_{01}}{\sqrt{b_1^2+c_1^2}}\right) } \end{aligned}$$

(16)

$$\begin{aligned} k_2&=\frac{m_2ga_2}{b_2c_2\left( 1-\frac{d_{02}}{\sqrt{b_2^2+c_2^2}}\right) } \end{aligned}$$

(17)

where $d_{01}$ and $d_{02}$ are the initial free lengths, to be considered null in case of ZFL springs.

4 Virtual prototype of the exoskeleton

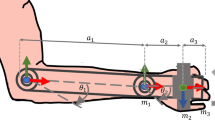
In the following, an interactive model is developed for studying the exoskeleton kinematics and statics in the design workspace. The mechanism schematic is shown in Fig. 8 and its main dimension parameters are summarized in Table 1. The length of each link (especially the ones attached to the operator’s arm and the forearm, i.e. $l_4$ and $l_5$) have been decided in accordance with the work presented in [72], considering a male whose body mass is 80 kg and height is 1.8 m. From the same study, the operator’s arm and forearm masses, and also their center of mass positions, have been determined. Obviously, these parameters can be varied and the model updated in case of different anatomical characteristics.

Fig. 8

Exoskeleton mechanism schematic with global and local coordinate systems

4.1 Kinematic model

The kinematic model of the 6 DoFs exoskeleton can be constructed based on the D-H method [73]. In particular, having defined a coordinate system for each link, $CS_i, \;i\in [0,6]$ (see Fig. 8), a set of six $4\times 4$ homogeneous transformation matrices, $A_i(\theta _i), \;i\in [0,5]$, can be easily formulated. Following the kinematic chain’s rule, being $^{6}{\mathbf {q}}=\begin{bmatrix}0&0&0&1 \end{bmatrix}^{T}$ the position vector of the end-effector with respect of the local coordinate system $CS_6$, the position vector with respect of the Global Coordinate System (GCS, aligned with $CS_0$ only in the initial configuration), ${\mathbf {Q}}=\begin{bmatrix}X&Y&Z&1 \end{bmatrix}^{T}$, is obtained as:

$$\begin{aligned} {\mathbf {Q}}={\mathbf {A}} ^{6}{\mathbf {q}} \end{aligned}$$

(18)

being ${\mathbf {A}}$ the overall transformation matrix, calculated as:

$$\begin{aligned} {\mathbf {A}}=\mathbf {A_0}\mathbf {A_1}\mathbf {A_2}\mathbf {A_3}\mathbf {A_4}\mathbf {A_5} \end{aligned}$$

(19)

where

$$\begin{aligned} \mathbf {A_0}&=\begin{bmatrix}\cos \theta _0 &{}-\sin \theta _0&{} 0 &{}0\\ sin\theta _0 &{}\cos \theta _0 &{}0&{} 0\\ 0&{} 0 &{}1 &{}0\\ 0 &{}0 &{}0 &{}1\end{bmatrix}\\ \mathbf {A_1}&=\begin{bmatrix}1&{} 0&{} 0&{} 0\\ 0&{} 1&{} 0 &{}-l_1\cos \theta _1\\ 0&{} 0&{} 1&{} -l_1\sin \theta _1\\ 0&{} 0 &{}0&{} 1\end{bmatrix}\\ \mathbf {A_2}&=\begin{bmatrix}1&{} 0&{} 0&{} r_1\\ 0 &{}\cos \theta _2 &{}-\sin \theta _2 &{}-r_3\sin \theta _2\\ 0 &{}\sin \theta _2&{} \cos \theta _2&{} r_3\cos \theta _2\\ 0 &{}0&{} 0 &{}1\end{bmatrix}\\ \mathbf {A_3}&=\begin{bmatrix}\cos \theta _3 &{}-\sin \theta _3&{} 0&{} r_2\sin \theta _3\\ \sin \theta _3&{} \cos \theta _3 &{}0&{} -r_2\cos \theta _3\\ 0 &{}0&{} 1 &{}-r_3\\ 0&{} 0&{} 0 &{}1\end{bmatrix}\\ \mathbf {A_4}&=\begin{bmatrix}1 &{}0 &{}0&{} l_4\sin \theta _4\\ 0 &{}1 &{}0&{} 0\\ 0 &{}0&{} 1&{} l_4\cos \theta _4\\ 0 &{}0&{} 0 &{}1\end{bmatrix}\\ \mathbf {A_5}&=\begin{bmatrix}\cos \theta _5 &{}0 &{}\sin \theta _5&{} l_5\sin \theta _5\\ 0&{} 1 &{}0 &{}0\\ -\sin \theta _5&{} 0 &{}\cos \theta _5 &{}l_5\cos \theta _5\\ 0 &{}0 &{}0 &{}1\end{bmatrix} \end{aligned}$$

In accordance with initial mechanism configuration visible in Fig. 8, each rotation angle is defined as $\theta _i=\theta _{i,0}+\Delta \theta _i, \;i\in [0,5]$. The motion parameters of each R joint are summarized in Table 2, and the resulting exoskeleton design workspace is illustrated in Fig. 9 (where $\theta _5=\theta _{5,0}$ for visualization purpose). These operative limits have been chosen with the aim of avoiding kinematic singularities, which otherwise may occur, as clearly pointed out in [43].

Table 1 Geometrical and mass parameters of the virtual model

Table 2 Motion parameters of the exoskeleton model considered in the analysis

Fig. 9

3D map of the exoskeleton range of motion

4.2 Static model

The main purpose of the static analysis is to return, for any generic imposed trajectory of the exoskeleton’s end-effector, the torques that need to be externally provided at the six R joints ($R_i, \; i\in [0,5]$ in Fig. 4d) so as to achieve a complete gravity balancing. In the subsequent preliminary model, the masses $m_1$ and $m_2$ are attached to the Link 4 and Link 5 respectively (with distance $r_2$, as visible in Fig. 8). Since $R_0$ rotates around the GCS z-axis, the weight will be equilibrated by the reaction force for any in-operation configuration, removing the need of external balancing actions. As for $R_1$, the scapular decoupling mechanism (gray parallelogram in Fig. 8) simplifies the calculation of the gravity torque (as explained in Sect. 3.2), which becomes:

$$\begin{aligned} M_{1}=l_1(m_1+m_2)g\cos \theta _1 \end{aligned}$$

(20)

Fig. 10

Mechanism schematics showing the influence of $\theta _2$ (a), $\theta _3$ (b) and $\theta _4$-$\theta _5$ (c) on $M_2$

The torque at $R_2$ can be formulated as:

$$\begin{aligned} M_2=h_{2,m_1}m_1g+h_{2,m_2}m_2g \end{aligned}$$

(21)

where, according to Fig. 10a:

$$\begin{aligned}&h_{2,m_1}=r_{m_1}\cos \left( \theta _2+\arctan \left( \frac{-v_{4,m_1}}{h_{3,m_1}}\right) \right) \end{aligned}$$

(22)

$$\begin{aligned}&h_{2,m_2}=r_{m_2}\cos \left( \theta _2+\arctan \left( -\frac{v_4+v_{5,m_2}}{h_{3,m_2}}\right) \right) \end{aligned}$$

(23)

$$\begin{aligned}&r_{m_1}=\sqrt{{h_{3,m_1}}^2+{v_{4,m_1}}^2} \end{aligned}$$

(24)

$$\begin{aligned}&r_{m_2}=\sqrt{{h_{3,m_2}}^2+(v_4+v_{5,m_2})^2} \end{aligned}$$

(25)

and according to Fig. 10b and c:

$$\begin{aligned}&h_{3,m_1}=h_{4,m_1}\sin \theta _3\end{aligned}$$

(26)

$$\begin{aligned}&h_{3,m_2}=\left( h_4+h_{5,m_2}\right) \sin \theta _3\end{aligned}$$

(27)

$$\begin{aligned}&h_{4,m_1}=a_4\sin \theta _4\end{aligned}$$

(28)

$$\begin{aligned}&h_4=l_4\sin \theta _4\end{aligned}$$

(29)

$$\begin{aligned}&h_{5,m_2}=a_5\sin \theta _5\end{aligned}$$

(30)

$$\begin{aligned}&v_{4,m_1}=-a_4\cos \theta _4\end{aligned}$$

(31)

$$\begin{aligned}&v_4=-l_4\cos \theta _4\end{aligned}$$

(32)

$$\begin{aligned}&v_{5,m_2}=-a_5\cos \theta _5 \end{aligned}$$

(33)

For the remaining R joints, the analysis can be further simplified by employing the rotation matrices, namely:

$$\begin{aligned} \mathbf {R_2}&=\begin{bmatrix}1&{} 0&{} 0\\ 0 &{}\cos \theta _2 &{}-\sin \theta _2 \\ 0 &{}\sin \theta _2&{} \cos \theta _2\end{bmatrix}\\ \mathbf {R_3}&=\begin{bmatrix}\cos \theta _3 &{}-\sin \theta _3&{} 0\\ \sin \theta _3&{} \cos \theta _3 &{}0\\ 0 &{}0&{} 1 \end{bmatrix}\\ \mathbf {R_4}&=\begin{bmatrix}\cos \theta _4 &{}0 &{}\sin \theta _4\\ 0&{} 1 &{}0\\ -\sin \theta _4&{} 0 &{}\cos \theta _4 \end{bmatrix}\\ \mathbf {R_5}&=\begin{bmatrix}\cos \theta _5 &{}0 &{}\sin \theta _5\\ 0&{} 1 &{}0\\ -\sin \theta _5&{} 0 &{}\cos \theta _5 \end{bmatrix} \end{aligned}$$

In fact, by defining the forces in the GCS via the vectors $\mathbf {f_1}=\begin{bmatrix}0&0&-m_1g \end{bmatrix}^{T}$ and $\mathbf {f_2}=\begin{bmatrix}0&0&-m_2g \end{bmatrix}^{T}$, and by applying the above rotations, the resulting force vectors in the local coordinate systems become:

$$\begin{aligned}&{\mathbf {f}_{\mathbf {1,CS_3}}}=\mathbf {R_3^T}\mathbf {R_2^T}\mathbf {f_1}\quad&{\mathbf {f}_{\mathbf {2,CS_3}}}=\mathbf {R_3^T}\mathbf {R_2^T}\mathbf {f_2} \end{aligned}$$

(34)

$$\begin{aligned}&{\mathbf {f}_{\mathbf {1,CS_4}}}=\mathbf {R_4^T}\mathbf {R_3^T}\mathbf {R_2^T}\mathbf {f_1}\quad&{\mathbf {f}_{\mathbf {2,CS_4}}}=\mathbf {R_4^T}\mathbf {R_3^T}\mathbf {R_2^T}\mathbf {f_2} \end{aligned}$$

(35)

$$\begin{aligned}&{\mathbf {f}_{\mathbf {2,CS_5}}}=\mathbf {R_5^T}\mathbf {R_3^T}\mathbf {R_2^T}\mathbf {f_2} \end{aligned}$$

(36)

Then, being each of these vectors in the form ${\mathbf {f}_{\mathbf {m,CS_n}}}=\begin{bmatrix}f_{mx,CS_n}&f_{my,CS_n}&f_{mz,CS_n} \end{bmatrix}^{T}$, with $m\in [1,2]$ and $n\in [3,5]$, the torques at joints $R_3$, $R_4$ and $R_5$ can be found as follows:

$$\begin{aligned}&M_3=f_{1y,CS_3}\sqrt{{v_{3,m_1}}^2+{h_{3,m_1}}^2}\nonumber \\&\quad + f_{2y,CS_3}\sqrt{{v_{3,m_2}}^2+{h_{3,m_2}}^2} \end{aligned}$$

(37)

$$\begin{aligned}&M_{4}=f_{1x,CS_4}a_4+f_{2x,CS_4}l_4 \end{aligned}$$

(38)

$$\begin{aligned}&M_5=f_{2x,CS_5}a_5 \end{aligned}$$

(39)

where

$$\begin{aligned}&v_{3,m_1}=h_{4,m_1}\cos \theta _3 \end{aligned}$$

(40)

$$\begin{aligned}&v_{3,m_2}=\left( h_4+h_{5,m_2}\right) \cos \theta _3 \end{aligned}$$

(41)

Once the expressions of $M_i, \; i\in [1,5]$ are available, one may choose to design an active balancing system consisting of five actuators. However, from a rapid overview of the proposed static model, it can be noted that the decoupling mechanisms have introduced two important simplifications, namely:

• A contribute $M_1$ which is function of the only angle $\theta _1$ (see Eq. 20) and can be balanced via a simple passive element;

• A straightforward procedure for the synthesis of the passive springs (see Sect. 3), to be placed at joints $R_1$, $R_4$ and $R_5$.

Building upon these considerations, in this paper three NZFL springs are included in the mechanical design of the exoskeleton. Their stiffness constants are defined as follows:

$$\begin{aligned} k_1&=\frac{l_1(m_1+m_2)g}{b_1c_1\left( 1-\frac{d_{01}}{\sqrt{b_1^2+c_1^2}}\right) } \end{aligned}$$

(42)

$$\begin{aligned} k_4&=\frac{a_4m_1g+l_4m_2g}{b_4c_4\left( 1-\frac{d_{04}}{\sqrt{b_4^2+c_4^2}}\right) } \end{aligned}$$

(43)

$$\begin{aligned} k_5&=\frac{a_5m_2g}{b_5c_5\left( 1-\frac{d_{05}}{\sqrt{b_5^2+c_5^2}}\right) } \end{aligned}$$

(44)

where, $b_1$, $b_4$, $b_5$, $c_1$, $c_4$, $c_5$ are the installation distances, as visible in Fig. 7, whereas $d_{01}$, $d_{04}$, $d_{05}$ are the initial free lengths of the springs. A part from $M_1$, which falls into the planar case study analyzed in Sect. 3.2, in the specific case of $M_4$ and $M_5$ a complete balancing cannot be achieved via the only use of passive springs due to the spatial motions of the second decoupling mechanism (arm and forearm) and, therefore, the motors are still necessary. The torques provided by the springs are:

$$\begin{aligned}&M_{k_{1}}=\frac{k_1b_1c_1\cos \theta _1(d_1-d_{01})}{d_1} \end{aligned}$$

(45)

$$\begin{aligned}&M_{k_{4}}=\frac{k_4b_4c_4\cos \theta _4(d_4-d_{04})}{d_4} \end{aligned}$$

(46)

$$\begin{aligned}&M_{k_{5}}=\frac{k_5b_5c_5\cos \theta _5(d_5-d_{05})}{d_5} \end{aligned}$$

(47)

where, $d_1$, $d_4$, $d_5$ are to be evaluated with the cosine theorem. Therefore, the resulting torques after spring balancing are:

$$\begin{aligned}&M_{1,b}=M_1-M_{k_{1}} \end{aligned}$$

(48)

$$\begin{aligned}&M_{4,b}=M_4-M_{k_{4}} \end{aligned}$$

(49)

$$\begin{aligned}&M_{5,b}=M_5-M_{k_{5}} \end{aligned}$$

(50)

Fig. 11

3D animations of the tested operator’s movements

4.3 Numerical validation

Fig. 12

Registered reaction torques at $R_1$ during the first (a), second (b) and third (c) imposed movements

Fig. 13

Registered reaction torque at $R_2$ during the first (a), second (b) and third (c) imposed movements

To validate the previous analysis, a 3D solid model of the exoskeleton has been tested in RecurDyn environment by imposing three overhead movements, shown in Fig. 11, within the considered workspace. The model is analyzed by enforcing a set of rotations ($\Delta \theta _i, \; i\in [0,5]$, listed in Table 3) and by measuring the resulting reaction torques at each R joint ($R_i, \; i\in [0,5]$). The effect of both ZFL and NZFL springs is modeled through the RecurDyn spring elements. The considered parameters are $b_1=0.5\;l_1$, $b_4=a_4$, $b_5=a_5$, $c_1=c_4=c_5=30$ mm, $d_{01}=20$ mm, $d_{04}=50$ mm and $d_{05}=35$ mm, with $l_1$, $a_4$ and $a_5$ as in Table 1. To exclude the inertial loads, a total simulation time of 5 s is imposed in the MBD simulations. The results of the three analysis are reported in Figs. 12, 13, 14, 15 and 16. Overall, the models show good agreement, being the medium error between them lower than $0.2\%$. The main outcomes of this test are as follows:

Table 3 Rotations applied in the simulations

• The passive elements have a remarkable influence on the computed behaviors, as it may be noticed by comparing $M_1$-$M_{1,b}$, $M_4$-$M_{4,b}$ and $M_5$-$M_{5,b}$ in Figs. 12, 15 and 16. For the totality of the cases, the springs provided large reductions of the reaction torques at joints $R_1$, $R_4$ and $R_5$.

• As expected, the ZFL springs ensure better performance than the NZFL, i.e. almost null trends in many areas of the plots. Even so, the parameters of the NZFL springs may be further refined through an optimization process to possibly increase the balancing accuracy. The presence of an efficient analytical model surely promotes this approach.

As for the motor selection, by taking into account the contributes of the NZFL springs, the maximum reached torque levels are 650 Nmm, 4500 Nmm, 1960 Nmm, 435 Nmm and 135 Nmm for $M_{1,b}$, $M_2$, $M_3$, $M_{4,b}$ and $M_{5,b}$ respectively. These values fall within the operative range of the FLA-series by Harmonic Drive SE. In particular, the FLA-11A-50FB and FLA-14A-100FB can satisfy the requirements at $R_4$–$R_5$ and at $R_2$–$R_3$ respectively.

Fig. 14

Registered reaction torque at $R_3$ during the first (a), second (b) and third (c) imposed movements

Fig. 15

Registered reaction torques at $R_4$ during the first (a), second (b) and third (c) imposed movements

Fig. 16

Registered reaction torques at $R_5$ during the first (a), second (b) and third (c) imposed movements

The reported virtual prototypes represent an effective interactive design tool for the evaluation of the design variants since early design stages and, if properly integrated within modern simulation environments, they allow to quickly identify the best exoskeleton configuration. For instance, by coding the reported analytical model in Matlab, a single candidate can be solved in less than 1 s, promoting the execution of parametric studies involving a large number of candidates. In this way, the final exoskeleton design can be reached, based on the specified motion and compensation requirements, through optimization approaches.

5 Conclusions

In this paper, the conceptual design and the virtual prototyping of an upper limb exoskeleton for assisted operations in industrial and healthcare environments is reported. This research has been motivated by the need to provide a simple, low cost, portable device that may be worn to prevent muscle pains during repetitive tasks or to facilitate medical treatments. In the last decades, a number of exoskeletons have been released, generally divided into research prototypes and industrial-oriented prototypes. The former present higher motion capabilities, whereas the latter rely on a compact and wearable structure. The proposed solution has been conceived with the aim of combining these important features. The mechanism consists of a 6 DoFs serial chain with two decoupling parallelograms, and provides the gravity balancing of the human upper limbs through the combined action of four electric motors and three NZFL springs. After a detailed description of the design methods, the paper focused on the kinematic and static analysis of the exoskeleton. An analytical model has been developed and then validated via a commercial MBD package. Three different overhead movements were simulated and the achieved results allowed for a proper motor selection. The interactive simulations of the exoskeleton showed that while the use of analytical approaches may be preferable to manage a large number of design parameters, the detailed animations made available by the MBD tool interface allow to visualize the exoskeleton’s complex 3D motion and to correct possible errors without screening large amounts of numerical data.

The presented models will be of primary importance for future developments, e.g. for the controller rapid prototyping and for the definition of event-based simulation environments (virtual and augmented reality), which are valuable methods to conduct ergonomic assessments and also to define training sessions for industrial operators and patients.