Skip to main content

Advertisement

SpringerLink
Log in

Delegation, R&D and competitiveness in a Bertrand duopoly

  • Original Paper
  • Published:
Review of Managerial Science Aims and scope Submit manuscript

Abstract

This paper studies the profitability of centralized investments in R&D versus decentralized price determination in a duopoly for Bertrand consumer markets. As a direct effect, R&D investments lower the firm’s production costs and thus increase c.p. the firm’s profits. However, as an indirect effect, lowering production costs causes market reactions and alters the competition between the firm and its competitors. In the extreme, aggressive competition can occur that diminish an investing firm’s profits. Delegating the price decision using an incentive contract distorts a manager’s perceived costs and induces a virtual cost increase in equilibrium. Trading off the factual cost reduction against a virtual cost increase we find that competition makes strategic delegation more attractive compared to investments in R&D. If firms are allowed to apply both strategies in combination, they concentrate on just one of them for strategic considerations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

Notes

  1. These strategies are also of practical interest as (voluntary) disclosure of innovation expenditures and management salary is common in some industries and countries. Studies of Zantout and Tsetsekos (1994) and Park et al. (2001) provide evidence that such disclosure can serve as credible commitment.

  2. Neus and Nippel (1996) provide an excellent review about the concept of strategic behavior and determinants of commitment strategies.

  3. Modeling decentralization we follow the strategic delegation literature. Thus, agency aspects are not considered.

  4. Fudenberg and Tirole (1984) define over- and underinvestment as a firm’s investment decision compared to that in an open-loop equilibrium, in which the firm takes the competitor’s action as given and does not try to influence him through its choice of investment. Thus, over- or underinvestment is the component that determines a strategy as a commitment strategy.

  5. In a recent study, comparing different bonus systems as pure profits, sales, market share and relative performance, Jansen et al. (2009) conclude that relative performance is superior throughout. In a different setting Dierkes (2004) investigates that relative performance is also superior to the performance evaluation based on adjusted costs.

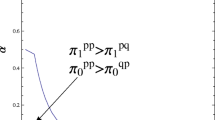
  6. As equilibria are symmetric with respect to \(\Uptheta , \) considering complements does not change our findings. However, it is worth to mention that in a model including commitment strategies, in price (quantity) competition these strategies always appear to be underinvestment (overinvestment) strategies, regardless if products are substitutes or complements. Thus, Singh and Vives’ (1984) finding of quantity competition with strategic substitutes being the dual of price competition with strategic complements, does not hold in this multi-stage setup.

  7. For a more detailed presentation of parameter restrictions in R&D games see Qiu (1997).

  8. Presenting the manager’s compensation more accurately, total compensation of a manager is given by TC i  = F i  + B i M i , where F i is a fixed component and B i is the bonus rate. Each owner selects the compensation package such that \(TC_{i}\geq \overline{U}\) holds, where the constant \(\overline{U}\) denotes the reservation utility of the manager (the amount the manager can earn elsewhere). Since owners will not overpay managers, \(TC_{i}=\overline{U}\) holds. Therefore, from an incentive point of view the constant in the owner’s objective function and F i and B i of the manager’s compensation contract can be neglected.

  9. Suppose the implementation of each strategy requires up front fixed cost investments F. This investments are small compared to achievable profits, F ≪ π i , and thus do not affect strategic considerations. However, firms might be budget constrained at t = 1 with budget B. If F < B < 2F holds, then they are not able to finance both strategies and have to select one among the available strategies.

  10. If the equilibrium value of x i  ≠ x I+ i , then x i is defined as a commitment strategy.

  11. Here \(x_{i}^{II+}\) indicates the optimal R&D investments of firm i if both firms innovate without strategic considerations. Thus, each firm determines its R&D level without taking the reaction of the competitor into account.

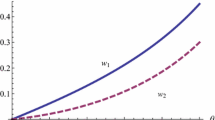
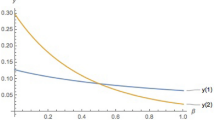
  12. As the expressions for the respective frontiers are quite intricate we abstract from presenting them in the paper. But they can be provided on request.

  13. We provide equilibrium values in Appendix B.

  14. Kopel and Löffler (2008) observe an identical behavior in a Stackelberg duopoly with Cournot competition and homogeneous products, where owners offer their managers sales quantity based incentive contracts. But their result of sticking to one single commitment strategy is inter alia driven by the very special property of their model that delegation and R&D have the same strategic effect (Kopel and Löffler 2008, p. 159). Thus, these strategies are perfect substitutes.

    Applying the Stackelberg set-up to our model, we investigate that, similar to the game at hand, the follower can choose between two strategy paths. Checking for stability and subgame perfection, we can confine this to just one subgame perfect equilibrium strategy where the follower implements only the delegation strategy for strategic considerations. Furthermore, beside the time leadership the leader does not use any additional strategy as a commitment device. This result acknowledges Kopel and Löffler’s finding and proofs that their result is not just the outcome of the special model specifications.

References

  • Adams W, Brock JW (2000) Tobacco: predation and persistent market power. In: Rosenbaum DI (ed) Market dominance. How firms gain, hold, or lose it and the impact on economic performance. Praeger Publishers, Westport

    Google Scholar 

  • Bowley AL (1924) The mathematical groundwork of economics. Oxford University Press, Oxford

    Google Scholar 

  • Brander JA, Spencer BJ (1983) Strategic commitment with R&D: the symmetric case. Bell J Econ 14(1):225–235

    Article  Google Scholar 

  • Caruana G, Einav L (2008) A theory of endogenous commitment. Rev Econ Stud 75:99–116

    Article  Google Scholar 

  • Dierkes S (2004) Strategische Kostenanpassung oder relative Leistungsbewertung—Was ist besser? Zeitschrift für betriebswirtschaftliche Forschung 56:45–59

    Google Scholar 

  • Dixon H (1985) Strategic investment in an industry with a competitive product market. J Ind Econ 33:483–499

    Article  Google Scholar 

  • Fershtman C (1985) Managerial incentives as a strategic variable in duopolistic environment. Int J Ind Organ 3:245–253

    Article  Google Scholar 

  • Fershtman C, Judd KL (1987) Equilibrium incentives in oligopoly. Am Econ Rev 77:927–940

    Google Scholar 

  • Fudenberg D, Tirole J (1984) The fat-cat effect, the puppy-dog ploy and the lean and hungry look. Am Econ Rev 74:361–368

    Google Scholar 

  • Ghemawat P (1993) Commitment to a precess innovation: Nucor, USX, and thin slab casting. J Econ Manag Strategy 2:133–161

    Article  Google Scholar 

  • Jansen T, van Lier A, van Witteloostuijn A (2007) A note on strategic delegation: the market share case. Int J Ind Organ 25:531–539

    Article  Google Scholar 

  • Jansen T, van Lier A, van Witteloostuijn A (2009) On the impact of managerial bonus systems on firm profit and market competition: the cases of pure profit, sales, market share and relative profits compared. Manag Decis Econ 30:141–153

    Article  Google Scholar 

  • Kadiyali V (1996) Entry, its deterrence, and its accommodation: a study of the U.S. photographic film industry. Rand J Econ 27:452–478

    Article  Google Scholar 

  • Kopel M, Löffler C (2008) Commitment, first-mover, and second-mover advantage. J Econ 94(2):143–166

    Article  Google Scholar 

  • Kopel M, Löffler C (2010) Organizational governance, leadership, and the influence of competition. Working Paper

  • Kopel M, Riegler C (2008) Delegation in an R&D game with spillovers. In: Cellinin R, Lambertini L (eds) The economics of innovation. Emerald, Bingley, pp 177–213

    Chapter  Google Scholar 

  • Lambertini L, Primavera G (2001) Delegation vs. cost-reducing R&D in a cournot duopoly. Rivista Internazionale di Scienze Economiche e Commerciali 48:163–178

    Google Scholar 

  • Miller NH, Pazgal AI (2001) The equivalence of price and quantity competition with delegation. Rand J Econ 32:284–301

    Article  Google Scholar 

  • Mitrokostas E, Petrakis E (2005) The scope of strategic delegation in oligopoly. Working Paper

  • Neus W, Nippel P (1996) Was ist strategisch an strategischem Verhalten. Zeitschrift für betriebswirtschaftliche Forschung 48:423–441

    Google Scholar 

  • Park Y, Nelson T, Huson M (2001) Executive pay and the disclosure environment: Canadian evidence. J Financial Res 24(3):347–365

    Google Scholar 

  • Qiu LD (1997) On the dynamic efficiency of Bertrand and Cournot equilibria. J Econ Theory 75:213–229

    Article  Google Scholar 

  • Sing N, Vives X (1984) Price and quantity competition in a differentiated oligopoly. Rand J Econ 15(4):546–554

    Article  Google Scholar 

  • Sklivas S (1987) The strategic choice of managerial incentives. Rand J Econ 18:452–458

    Article  Google Scholar 

  • Vickers J (1985) Delegation and the theory of the firm. Econ J Suppl 95:138–147

    Google Scholar 

  • Zantout Z, Tsetsekos G (1994) The wealth effects of announcements of R&D expenditure increases. J Financial Res 17(2):205–216

    Google Scholar 

Download references

Acknowledgments

We are grateful to Thomas Pfeiffer and the participants of the EARIE 2008 in Ljubljana for detailed comments and feedback. This paper has significantly improved thanks to the suggestions of Ralf Ewert (editor) and two anonymous referees.

Author information

Authors and Affiliations

  1. Department of Business Administration, University of Vienna, Brünner Straße 72, 1210, Vienna, Austria

    Clemens Löffler

Authors
  1. Clemens Löffler
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Clemens Löffler.

Appendix

Appendix

1.1 Appendix A

1.1.1 Standard Bertrand equilibrium

In the well known Bertrand equilibrium solutions are:

$$ \begin{aligned} p^{B} & = c+\frac{\left( a-c\right) \left( 1-\Uptheta \right) }{2-\Uptheta } \\ q^{B} & = \frac{a-c}{2+\Uptheta -\Uptheta^{2}} \\ \pi^{B} & = \frac{(a-c)^{2}(1-\Uptheta )}{(2-\Uptheta )^{2}(\Uptheta +1)}. \\ \end{aligned} $$

1.1.2 Subgame II: both commit by innovation

The values for p, q, x and π in this subgame are

$$ \begin{aligned} p^{II} & = c+\frac{\left( a-c\right) \left( r\left( \left( 2-\Uptheta^{2}\right)^{2}-\Uptheta^{2}\right) -2\left( 2-\Uptheta^{2}\right) \right) }{ r(\Uptheta +1)(\Uptheta +2)(\Uptheta -2)^{2}-2\left( 2-\Uptheta^{2}\right) } \\ q^{II} & = \frac{(a-c)r\left( 4-\Uptheta^{2}\right) }{r(\Uptheta +1)(\Uptheta +2)(\Uptheta -2)^{2}-2\left( 2-\Uptheta^{2}\right) }\\ x^{II} & = \frac{2(a-c)\left( 2-\Uptheta^{2}\right) }{r(\Uptheta +1)(\Uptheta +2)(\Uptheta -2)^{2}-2\left( 2-\Uptheta^{2}\right) }\\ \pi^{II} & = \frac{(a-c)^{2}r\left( r(1-\Uptheta^{2})\left( \Uptheta^{2}-4\right)^{2}-2\left( \Uptheta^{2}-2\right)^{2}\right) }{\left( r(\Uptheta +1)(\Uptheta +2)(\Uptheta -2)^{2}-2\left( 2-\Uptheta^{2}\right) \right)^{2}}. \end{aligned} $$

1.1.3 Subgame DD: both commit by delegation

The outcome of this subgame is

$$ \begin{aligned} p^{DD} & = c+\frac{\left( a-c\right) 2\left( 1-\Uptheta \right) }{4-\Uptheta (2+\Uptheta )} \\ q^{DD} & = \frac{(a-c)\left( 2-\Uptheta^{2}\right) }{(\Uptheta +1)(4-\Uptheta (2+\Uptheta ))} \\ \alpha^{DD} & = 1+\frac{(a-c)\left( 1-\Uptheta \right) \Uptheta^{2}}{4-\Uptheta (2+\Uptheta) } \\ \pi^{DD} & = \frac{2(a-c)^{2}(1-\Uptheta )\left( 2-\Uptheta^{2}\right) }{ (1+\Uptheta )\left( 4-\Uptheta (2+\Uptheta \right)^{2})}. \end{aligned} $$

1.1.4 Subgames ID and DI: one firm innovates, the other delegates

The solution of this subgame is

$$ \begin{aligned} p_{1}^{ID} &= p_{2}^{DI}=c+\frac{(a-c)(1-\Uptheta )(4+(2-\Uptheta )\Uptheta )\left( 2\left( 2-\Uptheta^{2}\right) -r\left( \Uptheta^{4}-5\Uptheta^{2}+4\right) \right) }{2\left( 2-\Uptheta^{2}\right) \left( 4-3\Uptheta^{2}-2r\left( \Uptheta^{4}-5\Uptheta^{2}+4\right) \right) } \\ p_{1}^{DI} &= p_{2}^{ID}=c+\frac{(a-c)\left( 1-\Uptheta^{2}\right) \left( 4-2\Uptheta^{2}-r(2-\Uptheta )(1-\Uptheta )(2+\Uptheta )^{2}\right) }{\left( 2-\Uptheta^{2}\right) \left( 4-3\Uptheta^{2}-2r\left( \Uptheta^{4}-5\Uptheta^{2}+4\right) \right)} \\ q_{1}^{ID} &= q_{2}^{DI}=\frac{(a-c)r(\Uptheta -2)(\Uptheta -1)(\Uptheta +2)((\Uptheta -2)\Uptheta -4)}{2\left( \Uptheta^{2}-2\right) \left( 2r\left( \Uptheta^{4}-5\Uptheta^{2}+4\right) +3\Uptheta^{2}-4\right) } \\ q_{1}^{DI} &= q_{2}^{ID}=\frac{(a-c)\left( r(\Uptheta -2)(\Uptheta -1)(\Uptheta +2)^{2}+2\Uptheta^{2}-4\right) }{4r\left( \Uptheta^{4}-5\Uptheta^{2}+4\right) +6\Uptheta^{2}-8} \\ \alpha_{1}^{DI} & = \alpha_{2}^{ID} \\ & = 1 + \frac{(a-c)\Uptheta^{2}\left( 1-\Uptheta^{2}\right) \left( r(2-\Uptheta )(1-\Uptheta )(\Uptheta +2)^{2}+2\Uptheta^{2}-4\right) }{a(1-\Uptheta )\Uptheta^{2}(\Uptheta +1)\left( r(2-\Uptheta)(1-\Uptheta )(\Uptheta +2)^{2}+2\Uptheta^{2}-4\right) -c\left( r(2-\Uptheta )(\Uptheta -1)(\Uptheta +1)(\Uptheta +2)\left( \left( \Uptheta^{2}+\Uptheta -6\right) \Uptheta^{2}+8\right) +2\left(2-\Uptheta^{2}\right)^{3}\right) } \\ x^{ID} & = x^{DI}=\frac{(a-c)(\Uptheta -1)((\Uptheta -2)\Uptheta -4)}{2r\left( \Uptheta^{4}-5\Uptheta^{2}+4\right) +3\Uptheta^{2}-4}\\ \pi_{1}^{ID} & = \pi_{2}^{DI}=\frac{(a-c)^{2}r(\Uptheta -1)^{2}((\Uptheta -2)\Uptheta -4)^{2}\left( r\left( 1-\Uptheta^{2}\right) \left( 4-\Uptheta^{2}\right)^{2}-2\left( 2-\Uptheta^{2}\right)^{2}\right) }{4\left( \Uptheta^{2}-2\right)^{2}\left( 2r\left( \Uptheta^{4}-5\Uptheta^{2}+4\right) +3\Uptheta^{2}-4\right)^{2}} \\ \pi_{1}^{DI} & = \pi_{2}^{ID}=\frac{\left( \Uptheta^{2}-1\right) (a-c)^{2}\left( r(\Uptheta -2)(\Uptheta -1)(\Uptheta +2)^{2}+2\Uptheta^{2}-4\right)^{2}}{2\left( \Uptheta^{2}-2\right) \left( 2r\left( \Uptheta^{4}-5\Uptheta^{2}+4\right) +3\Uptheta^{2}-4\right)^{2}}. \\ \end{aligned} $$

1.2 Appendix B

Solving the reduced profit function (18) of the combined setup delivers the four equilibria which are shown below.

Equilibrium 1:

$$ \begin{aligned} \alpha^{C_{1}C_{1}} & = -\frac{\left( 4-\Uptheta^{2}\right) (cr(2-\Uptheta )(1+\Uptheta )-a)}{a\Uptheta^{2}} \\ x^{C_{1}C_{1}} & = c \\ p^{C_{1}C_{1}} & = a\left( 1-\frac{1}{2-\Uptheta^{2}}\right) \\ \pi^{C_{1}C_{1}} & = \frac{a^{2}(1-\Uptheta )}{(2-\Uptheta )^{2}(1+\Uptheta )}- \frac{c^{2}r}{2}. \end{aligned} $$

Equilibrium 2 and 3

$$ \begin{aligned} \alpha_{1}^{C_{1}C_{2}} &\,=\, \alpha_{2}^{C_{2}C_{1}}\,=\,1-\frac{\left( 2-\Uptheta^{2}\right) \left( cr\left( 4r\left( \Uptheta^{4}-5\Uptheta^{2}+4\right) +(4-(\Uptheta -2)\Uptheta )\left( \Uptheta^{2}-2\right) \right) -2a\left( r(\Uptheta -1)((\Uptheta -2)\Uptheta -4)+\Uptheta^{2}-2\right) \right) }{ \Uptheta^{2}\left( a\left( r(1-\Uptheta )(2-\Uptheta^{2}-(\Uptheta -2)\Uptheta -4)\right) -cr\Uptheta \left( \Uptheta^{2}-2\right) \right) } \\ \alpha_{1}^{C_{2}C_{1}} &\,=\, \alpha_{2}^{C_{1}C_{2}}\,=\,1-\frac{r\Uptheta^{2}(1+\Uptheta )\left( c\left( 2-\Uptheta^{2}\right) -a\left( 2-\Uptheta \left( 1+\Uptheta \right) \right) \right) }{\left( 2-\Uptheta^{2}\right) (4cr(1+\Uptheta )-a(2+\Uptheta ))} \\ x_{1}^{C_{1}C_{2}} &\,=\, x_{2}^{C_{2}C_{1}}=c \\ x_{1}^{C_{2}C_{1}} &\,=\, x_{2}^{C_{1}C_{2}}\,=\,\frac{(a-c)\left( 2-\Uptheta^{2}\right) }{r(1+\Uptheta )(4-\Uptheta (2+\Uptheta ))+\Uptheta^{2}-2} \\ p_{1}^{C_{1}C_{2}} &\,=\, p_{2}^{C_{2}C_{1}}\,=\,c+\frac{a\left( 2-\Uptheta -\Uptheta^{2}\right) -c\left( 4-\Uptheta^{2}\right) -\frac{\Uptheta AB}{2-\Uptheta^{2}}}{ 4-\Uptheta^{2}} \\ p_{1}^{C_{2}C_{1}} &\,=\, p_{2}^{C_{1}C_{2}}\,=\,c+\frac{a\left( 2-\Uptheta -\Uptheta^{2}\right) -c\left( 4-\Uptheta^{2}\right) -\frac{2AB}{2-\Uptheta^{2}}}{ 4-\Uptheta^{2}} \\ \pi_{1}^{C_{1}C_{2}} &\,=\, \pi_{2}^{C_{2}C_{1}}\,=\,\frac{A\left( a\left( \Uptheta^{2}+\Uptheta -2\right) -AB\right) }{\Uptheta^{4}-5\Uptheta^{2}+4}-\frac{rA^{2}}{ 2}+\frac{\left( a\left( \Uptheta^{2}+\Uptheta -2\right) -AB\right) \left( a\left( \Uptheta^{2}+\Uptheta -2\right) -\frac{2AB}{\left( \Uptheta^{2}-2\right) }\right) }{\left( \Uptheta^{2}-4\right)^{2}\left( 1-\Uptheta^{2}\right) } \\ \pi_{1}^{C_{2}C_{1}} & \,=\, \pi_{2}^{C_{1}C_{2}}\,=\,\frac{\left( \frac{\Uptheta AB}{ \left( \Uptheta^{2}-2\right) }+a\left( \Uptheta^{2}+\Uptheta -2\right) \right)^{2}}{\left( 4-\Uptheta^{2}\right)^{2}\left( 1-\Uptheta^{2}\right) }-\frac{ c^{2}r}{2} \\ \end{aligned} $$

with

$$ \begin{aligned} A & = c+\frac{(a-c)\left( 2-\Uptheta^{2}\right) }{2-\Uptheta^{2}-r(1+\Uptheta )(4-\Uptheta (2+\Uptheta ))} \\ B & = \frac{(\Uptheta +2)\left( a\left( -r\Uptheta^{4}+(r+1)\Uptheta^{2}-2\right) +cr(\Uptheta -2)(\Uptheta +1)\left( \Uptheta^{2}-2\right) \right) }{a(\Uptheta +2)-4cr(\Uptheta +1)}. \end{aligned} $$

Equilibrium 4

$$ \begin{aligned} \alpha^{C_{2}C_{2}} & = 1+\frac{(a-c)r\Uptheta^{2}\left( 1-\Uptheta^{2}\right) }{cr(1+\Uptheta )(4-\Uptheta (\Uptheta +2))-a\left( 2-\Uptheta^{2}\right) } \\ x^{C_{2}C_{2}} & = \frac{(a-c)\left( 2-\Uptheta^{2}\right) }{r(1+\Uptheta )(4-\Uptheta (2+\Uptheta ))+\Uptheta^{2}-2} \\ p^{C_{2}C_{2}} & = c+\frac{(a-c)\left( 2-\Uptheta^{2}-2r\left( 1-\Uptheta^{2}\right) \right) }{2-\Uptheta^{2}-r(1+\Uptheta )(4-\Uptheta (2+\Uptheta ))} \\ \pi^{C_{2}C_{2}} & = \frac{(a-c)^{2}r\left( 2-\Uptheta^{2}\right) \left( 4r\left( 1-\Uptheta^{2}\right) +\Uptheta^{2}-2\right) }{2\left( r(1+\Uptheta )(4-\Uptheta (2+\Uptheta ))+\Uptheta^{2}-2\right)^{2}}. \\ \end{aligned} $$

Rights and permissions

Reprints and permissions

About this article

Cite this article

Löffler, C. Delegation, R&D and competitiveness in a Bertrand duopoly. Rev Manag Sci 6, 287–306 (2012). https://doi.org/10.1007/s11846-011-0067-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11846-011-0067-4

Keywords

JEL Classification

Search

Navigation