Sample-Based Methods of Analysis for Multistable Dynamical Systems

Abstract

In this paper we present how sample based analysis can complement classical methods for analysis of dynamical systems. We describe how sample based algorithms can be utilized to obtain better understanding of complex dynamical phenomena, especially in multistable dynamical systems that are difficult for analytical investigations. Relying on the simple, direct numerical integration algorithms we are able to detect all possible solutions including hidden and rare attractors; investigate the ranges of stability in multiple parameters space; analyse the influence of parameters mismatch or model imperfections; assess the risk of dangerous or unwanted behaviour and reveal the structure of multidimensional phase space. For each mentioned application we present methodology, example on paradigmatic non-linear dynamical system and discuss practical applications. The presented methods of analysis can be applied to solve numerous of scientific problems originating from different disciplines. Moreover, their robustness and efficiency will grow with the upcoming increase of computational power.

1 Introduction

The stability of dynamical systems have focused the interest of scientist for more than hundred years. One of the oldest example is the solar system. From our point of view, it is stable and we should not care about its destabilization, but looking in the timescale of a universe it becomes an important problem. Copernicus placed the Sun at the centre of the universe [18, 19]. Then, Kepller assumed that planets move along the perfect ellipses, hence after full revolution they follow the same trajectory [93]. This beautiful simplicity has been destroyed be the Newtons law of universal gravitation [70] which proofs that interactions occur between the Sun and all objects that orbit it. Thus, there is no reason to assume that the planet orbits are fixed ellipses. In the 18th century Lagrange and Laplace correctly formulated the equations of motion and proofed that Newton’s law is the universal explanation for the motion of the celestial bodies [68]. Since then, many scientists have considered this issue. The breakthrough work has been published by Poincaré [4, 87] where he showed that it is not possible to integrate the equations of motion of three bodies subjected to mutual interaction, and not possible to find an analytic solution representing the movement of the planets valid over infinite time interval. From this moment, we observe an intensive investigation of this problem, but the real milestone was done by applying numerical methods. Numerical computations show that the Solar system is unstable, but catastrophic phenomena leading to its destruction can take place only in a time comparable with its age (approximately 5 billion years) [47, 48, 91].

The modern study of stability starts from fundamental works of Poincaré, Lyapunov and Floquet. Henri Poincaré wrote a series of texts under common title “On curves defined by differential equations” [76]. He initiated a new branch of mathematics called qualitative theory of differential equations. He showed that even if the differential equation cannot be solved in terms of known functions, one can extract a wealth of information about the properties of solutions. Poincaré main interest was the nature of trajectories of integral curves in the plane space. He provided a classification of singular points (saddle, focus, centre, node) and introduced the concept of a limit cycle. Two years after Poincaré, in 1883 Gaston Floquet published paper [31] in which he define the stability of periodic solutions basing on eigenvalues of monodromy matrix [45]. Nine years after the publication of Floquet, in 1892 Aleksandr Lyapunov defended his PhD thesis entitled “The general problem of the stability of motion” [57]. He introduced definition of equilibrium stability, i.e. asymptotically and exponentially stable orbits. The intensive development of numerical techniques let us calculate Lyapunov exponents [6, 33, 71, 86] to characterize the stability of arbitrary type of solution. Basing on the sign of Lyapunov exponents we can also classify the types of quasi-periodic and chaotic solutions [7, 39, 74].

In aforementioned studies, the stability is calculated only in the close neighbourhood of the considered orbit. Such knowledge is enough if system is monostable, but if the system is multistable some perturbation may cause sudden change in behaviour and result in jump to different coexisting solution. Thus, we should gain better insight on the structure of the phase space in a wider range. It can be achieved via analysis of basins of attraction [5, 29, 95]. For systems with two generalized coordinates basins of attraction show all solutions as the behaviour of the system depends only on two initial conditions. Thus, we are able to reflect the structure of the phase space in a 2D plot and analyze the boundaries of basins of attraction. Most of practically inspired models have more then two dimensional phase space, which make investigations much more difficult because we can only look at the two-dimensional cuts of multi-dimensional phase space. This shows the importance of the analysis of stability and detection of basin boundaries. Such boundaries can be smooth or fractal [46, 60, 73]. If the the boundary of basin is a smooth curve or a surface the range of solution stability can be defined precisely. If boundary is more complex - fractal - initial conditions leading to different coexisting attractors are mixed [37] and we cannot predict the effects of even arbitraly small perturbation. To describe such structure and measure its complexity fractal dimension has been introduced. It provides a statistical index comparing how detail in a pattern changes with the scale at which it is measured. We can distinguish several measures like: Hausdorff dimension, box counting dimension, information dimension and ect. All of them can be used to characterize both basin and attractor [82]. If we focus on the structure of basins of attraction, we can distinguish following types: compact, eroded or riddle [40, 41]. For compact basins of attraction the attractor is surrounded with its basin. Hence, within this range we can be sure that after perturbation the system will go back to the attractor in finite time. For eroded or riddle basins it is much harder to predict if a perturbation can cause a jump to another solution. The importance of such analysis has been presented in 1989 by Thomson [89]. He discussed the basin erosion and indicated that with varying parameters of the system its basin can change from compact to completely eroded.

The studies of basins of attraction give a detailed knowledge if the dimension of system is low, but if we analyze multidimensional system we can miss important information. To overcome this problem a new methods of investigations have been proposed. Rega and Lenci proposed “basin integrity measures” [54, 55, 80] that describe the erosion of basins, i.e., global integrity measure and integrity factor. These measures enable to asses if the basin has safe, compact structure or it has fractal structure. Still, basin integrity measures are also hard to obtain for high-dimensional systems. Nevertheless, for low dimensional systems this method gives precise information about the multistable system dynamics. The advantages of this method has been proved on multiple investigations of various systems including systems with impacts [50,51,52], parametric excitation [53, 54], shells [34] and single-mode model of non-contact atomic force microscopy [81]. All these studies show that we can assess the structure of basins of attraction and basing on the obtained results we are able to propose effective control algorithms to reduce the erosion of basins.

The second method called “basin stability” has been developed by Menck et al. [62, 63]. Basin stability method enables to quantify stability basing on the probability of reaching given attractor from random initial conditions. To calculate basin stability measure one has to perform a significant number of Bernoulli trials and classify the final solutions reached in each trial. Proposed idea has been successfully applied to asses the stability of power grids [63, 85], systems with time delay [56], chimera states [79], stabilization of saddle fixed points in coupled oscillators [78] and brain dynamics [61]. In our previous papers we proposed extensions of this method [12]. Additionally to initial conditions we draw the parameters of the system. Such approach let us include in the analysis the uncertainty of parameters or just perform the very efficient investigation of coexisting solutions for systems with varying parameter values. We validate the accuracy of the proposed method with experimental study [15]. The next method “basin entropy” has been proposed by Daza et al. [22]. They propose another sample based algorithm to test the structure of basins of attraction to obtain information about its fractality. Basin entropy has been used for investigate the dynamics of propagating matter waves [21, 23] and the flux in twist Hamiltonian systems [67].

The three mentioned methods need very efficient algorithms and high computational power. Still, nowadays computational power is constantly increasing and let us use sample-based methods to analyze systems from different disciplines of science. Thanks to that, many complex problems can be solved using numerical algorithms instead of analytical derivations. Advanced computing enables to simplify scientific analysis and gives new possibilities for solving the most important problems.

In the paper we present four possible utilizations of sample-based analysis. In Sect. 2 we briefly present the basics of the basin stability and describe sample applications of this method. In Sect. 3 we show the expansion of the basin stability concept that enables effective analysis of systems with parameters mismatch. It enables to analyze the effects of system imperfections and varying working conditions. Sect. 4 is devoted to the description of how sample based methods can be used to determine ranges of stability and predict conditions that ensures the highest probability of reaching given solution. The presented approach has similar precision to classical methods of analysis but it is straight forward and can be applied for all types of dynamical systems. Moreover, basing on the data obtained with the algorithm we are able to characterize the structure of the phase space. It is described in Sect. 5 where we show how sample based approach supplements basins of attraction and dynamical integrity measures. It is especially important for multi-DoF systems where we cannot project the basins of attraction to present their boundaries and volume. In all sections we start with paradigmatic models to present the underlying methodology and supplement the description with real world example of possible utilization of the method. We conclude the presented material in Sect. 6.

2 Basin Stability Method

In this section, we show in detail the idea of basin stability method which enables to estimate the stability and number of solutions for given values of system parameters. The idea is strikingly simple but the method has found numerous successful applications and proved to be an efficient tool for dynamical analysis. The growing interest in this method comes from its two main advantages. Firstly, it is suitable for multidimensional and multistable systems where the classical approaches are difficult and time consuming to apply. Secondly, it can be easily applied to all types of systems and reproduces the inherent uncertainty of perturbations. To apply basin stability method we just need to have a reliable direct numerical integration code for the mathematical model of the investigated system. The computational effort does not grow significantly with the increase of the phase space dimensions. This makes this sample-based method even more appealing for the analysis of very high-dimensional systems such as large networks of oscillators, power grids or neural networks. Moreover, in our previous paper we prove that the results form basin stability method match with the results form the path-following analysis and experiment [15].

2.1 Methodology

The algorithm is simple and based on the series of N Bernoulli trials. For each trial we randomly select initial conditions and detect the final attractor using direct numerical integration. Based on this one can calculate the chance to reach given solution and determine the distribution of probability for all coexisting solutions. This gives information about the number of stable solutions and the sizes of their basins of attraction.

Consider the dynamical system with fixed parameters $\dot{{\mathbf {x}}}=f\,({\mathbf {x}},\,t)$, where ${\mathbf {x}}\in \mathtt {{\mathbb {R}}^{n}}$ is the state vector and $t\in {\mathbb {R}}$ is time. Let $\mathcal{B\subset \mathbb {\mathtt {{\mathbb {R}}^{n}}}}$ be a set of all possible initial conditions. Let us assume that attractor ${{\mathcal {A}}}$ exists, is stable and has a basin of attraction $\beta ({{\mathcal {A}}})$. Lets assume that within N overall trials attractor ${{\mathcal {A}}}$ was reached $n_{A}$ times. Assuming random initial conditions the probability that the system will reach attractor ${{\mathcal {A}}}$ is given by:

$$\begin{aligned} p\left( {{\mathcal {A}}}\right) =\frac{n_{A}}{N} \end{aligned}$$

(1)

This probability is the estimator of the basin stability measure that reflects the relative volume of the basin of attraction of attractor ${{\mathcal {A}}}$. If this is equal to one $(p\left( \mathcal{A}\right) =1.0)$ this means that considered solution is the only one in the taken range of initial conditions and given values of parameters. Otherwise, other attractors coexist and system is multistable. Due to physical limitation we cannot take the initial conditions form the infinite set but we draw them form set $\mathcal{B_{A}}\subset {{\mathcal {B}}}$. We can consider two possible ways to impose the limit to this set and both of them are based on preliminary analysis of the system. The first ensures that set ${{\mathcal {B}}_{A}}$ includes values of initial conditions leading to all possible solutions. This approach is appropriate if we want to get general overview of the system’s dynamics. In the second approach we use narrowed set of initial conditions that corresponds to practically accessible initial states.

2.2 Applications

The basin stability method has been already utilized in numerous applications. Originally, it has been created to analyze the synchronizability of Watts–Strogatz networks consisting of paradigmatic Rössler oscillators [62]. Authors vary the topology of the network starting form regular to random structure (which corresponds to diffident applications e.g. visual cortex, power grids and neural networks). The main conclusion is that the synchronous state is much more stable in networks that are more regular. In [85] the relationship between stability against large perturbations and topological properties of a power transmission grid has been analized. Authors introduce a very fast tool to predict the appearance of nodes with poor single-node basin stability. This algorithm can be applied during live operation of a power grid to increase safety of the network. The next study has been focused on details of modelling of power grids [3]. It proves that voltage dynamics should be taken into account in model of synchronous machines. In mountain ranges, big lakes or inland seas we often observe large closed loops in high voltage AC power grids [17]. The basins stability method has been used to identify three mechanisms which create the circulating power flows. Moreover, one can find significant number of studies that use basin stability method to show the way to increase the efficiency of power grids [2, 42, 43, 83]

Maslennikov et al. [61] study the basin stability of the burst synchronization regime in small-world networks consisting of chaotic slow-fast oscillators. The results confirm that the coupling density and the coupling strength influence the basin stability similarly and there are threshold values above which the basin stability of the burst synchronization regime significantly increase. The same method has been used to analize the explosive transitions between synchronous and non-synchronous states in networks [96]. Next, in [44] Authors consider synchronized state in time-varying complex networks (the time-varying character is ensured by stochastic rewiring of links with defined frequency). In [64] Mitra et al. propose the general framework of multiple-node basin stability for gauging the global stability and robustness of networks in response to non-local perturbations simultaneously affecting multiple nodes of a system. It helps to estimate the threshold number of simultaneously perturbed nodes that reduce the capacity of the system and triggers the return to the original solution.

In all dynamical systems the final state is always achieved after some transient time. Quite often, it is very hazardous range of the time evolution because the trajectory of the system can move very close to the boundary of stability and even a small perturbation can result in jump to another solution. To study transient dynamics an extension of basin stability method “constrained basin stability” has been created [92]. The time of recovery after perturbation has been discussed in [65].

The interesting application of the basin stability method to systems with time delay has been presented in [56]. The time delay is present in population dynamics, epidemiology, neurobiology, control engineering, optoelectronic and many more [1, 32, 35]. Due to presence of time delay the dimension of system phase space is infinite. Thus, the elaboration of the efficient tool to analyze solutions in this class of equations is extremely important. Authors propose a technique which projects the infinite dimensional initial state space to a finite-dimensional Euclidean space using three different bases: the Bernstein, the trigonometric and the Legendre and show on numerous examples that it is very effective. The basin stability has been also applied to piecewise and discontinuous systems (Amazonian vegetation model [66], externally forced oscillator with impacts [12] and system with dry friction [30]) where it gives information of co-existing solutions and volumes of their basins of attraction in multidimensional phase space.

3 Investigation of Systems with Parameters Mismatch

Basin stability measure was initially proposed as a tool to characterize the stability of different synchronous states of complex networks of oscillators. Thanks to its paradigmatic simplicity basin stability method can be easily expanded by drawing values of system’s parameters. The underlying idea is to take into consideration the fact that values of system’s parameters are measured or estimated with some finite accuracy which is often hard to determine. Moreover, values of parameters can vary during normal operation. Still, in practical applications we usually need certainty that presumed solution has enough surplus of stability to ensure safe operation. Hence, there is a need to describe how small changes of parameters’ values influence the behaviour of the system. Our method provides such description and allows to estimate the required accuracy of parameters’ values. Moreover, we can also consider the risk of unwanted phenomena under presence of model imperfections and parameters mismatch. Hence, it is time efficient, can be applied in a wide range of systems and does not require high computational power. The method is described in detail in our previous paper [12]. In this Section we briefly recall the proposed methodology, present results from paradigmatic systems and discussed some potential practical application.

3.1 Methodology

Consider the dynamical system $\dot{{\mathbf {x}}}=f\,({\mathbf {x}},\,t,\,\omega )$, where ${\mathbf {x}}\in \mathtt {{\mathbb {R}}^{n}}$ is the state vector, $t\in {\mathbb {R}}$ is time and $\omega \in {\mathbb {R}}^{m}$ are the system parameters, where m is the number of parameters that are taken into account. Let $\mathcal{B\subset \mathbb {\mathtt {{\mathbb {R}}^{n}}}}$ be a set of all possible initial conditions and $\mathcal{C}\subset \mathbb {\mathtt {{\mathbb {R}}}}^{m}$ a set of accessible values of system parameters. Let us assume that attractor ${{\mathcal {A}}}$ exists for $\omega \in {{\mathcal {C}}_{A}}\subset {{\mathcal {C}}}$ and has a basin of attraction $\beta ({{\mathcal {A}}})$. In classical approach of Menck et al. [62] the stability of attractor ${{\mathcal {A}}}$ is assessed basing on the probability of reaching ${{\mathcal {A}}}$ with random initial conditions but for fixed parameters (see Sect. 2.1).

We propose to not only draw initial conditions but also values of some selected parameters of the system from the set $\mathcal{C_{A}}\subset {{\mathcal {C}}}$ that consists of all practically accessible values of system’s parameters $\omega$. This let us ensure that given solution exists in this range (taking into account the mismatch in parameters). Next, we subdivide set $C_{A}$ in to $m=1,2,\ldots M$ equally spaced subsets. Subsets ${{\mathcal {C}}}_{A}^{m}$ do not overlap and the relation $\bigcup _{m=1\dots M}\mathcal{C}_{A}^{m}=C_{A}$ is always fulfilled. Then for each subset $\mathcal{C}_{A}^{m}$ we randomly pick N sets of initial conditions and value of the considered parameter. For each set we check the final attractor of the system. After sufficient number of Bernoulli trials we can calculate the probability of reaching presumed solution or solutions. As a result we can describe the relation between the value of the system’s parameter and volume of basin stability of reachable solutions. Value of N strongly depends on the complexity of analysed system, i.e. mainly on the size of phase space, the number of coexisting solutions and the structure of basins of attraction and size of initial conditions and parameters sets. Moreover, the computation time for single trial and should be adjusted for each system independently to ensure that the final attractor is reached. In general, we recommend that in most cases N should be at least one hundred.

3.2 Paradigmatic Examples

In this Section we present the methodology using two paradigmatic nonlinear dynamical systems: pendulum suspended to the Duffing oscillator and bilinear impacting oscillator. Both systems are excited with harmonic external force and have multiple stable attractors.

The first example presented in Fig. 1a is the Duffing oscillator with suspended pendulum that acts as a tuned mass absorber. The main body consists of mass M fixed to the ground with nonlinear spring (hardening characteristic $k_{1}+k_{2}y^{2}$) and viscous damper (damping coefficient $c_{y}$). The mass M is forced externally by harmonic excitation with amplitude F and frequency $\omega$. The pendulum has length l and mass m. The small viscous damping is present in the pivot of the pendulum that is described by parameter $c_{\varphi }$.

Fig. 1

The models of the considered paradigmatic systems: externally forced Duffing oscillator with attached pendulum (tuned mass absorber) (a) and bilinear impacting oscillator (b)

The derivation of equations of the system’s motion can be found in [13]. Here, we present the dimensionless equations of motion:

$$\begin{aligned}&\ddot{x}'-a\ddot{\varphi }'\sin \varphi '-a{\dot{\varphi }}'^{2}\cos \varphi '+x'+bx'^{3}+c{\dot{x}}'=f\cos \omega \tau ,\nonumber \\&\quad \ddot{\varphi }'-j\ddot{x}'\sin \varphi '+d\sin \varphi '+h{\dot{\varphi }}'=0, \end{aligned}$$

(2)

where dimensionless time $\tau =t\omega _{0} (\omega _{0}=\sqrt{\frac{k_{1}}{M+m}}$ is the natural linear frequency of Duffing oscillator), $a=\frac{m}{M+m}$, $b=\frac{k_{2}l^{2}}{k_{1}}$, $c=\frac{c_{y}}{(M+m)\omega _{0}}$, $f=\frac{F}{k_{1}l}$, $\omega =\frac{\nu }{\omega _{0}}$, $d=\frac{g}{\omega _{0}^{2}l}$, $h=\frac{c_{\varphi }}{ml^{2}\omega _{0}}$, $x'=\frac{y}{l}$, $\dot{x'}=\frac{{\dot{y}}}{\omega _{0}l}$, $\ddot{x'}=\frac{\ddot{y}}{\omega _{0}^{2}l}$, $\varphi '=\varphi ,$${\dot{\varphi }}'=\frac{{\dot{\varphi }}}{\omega _{0}}$ and $\ddot{\varphi }'=\frac{\ddot{\varphi }}{\omega _{0}^{2}}$. As control parameters we take the amplitude f and the frequency $\omega$ of external forcing. The dimensionless parameters have the following values: $a=0.303$, $b=0.031$, $c=0.132$, $j=0.3$, $d=0.3$, $h=0.02$. For simplicity primes in dimensionless equations will henceforth be neglected and we use x and $\varphi$ as dimensionless generalized coordinates of the system.

The second considered paradigmatic example is the system with impacts investigated previously in [72]. The system is shown in Fig. 1b and consists of mass M suspended by linear spring with stiffness $k_{1}$ and viscous damper with damping coefficient c to harmonically moving frame. The frame oscillates with amplitude A and frequency $\Omega$. When amplitude of mass M motion reaches value g we observe soft impacts (spring $k_{2}$ is significantly stiffer than spring $k_{1}$). To equation of motion is derived in [72]. Here, we present dimensionless form of equation and to obtain it we use the reference length $y_{0}=1$[mm]. Thus, the dimensionless equation of motion is as follow:

$$\begin{aligned} \ddot{x}+2\xi {\dot{x}}+x+\beta \left( x-e\right) \hbox {H}\left( x-e\right) =a\omega ^{2}\sin \left( \omega \tau \right) \end{aligned}$$

(3)

where $x=\frac{y}{y_{0}}$, ${\dot{x}}=\frac{{\dot{y}}}{\omega _{n}y_{0}}$, $\ddot{x}=\frac{\ddot{y}}{\omega _{n}^{2}y_{0}}$ are the dimensionless vertical displacement, velocity and acceleration of mass M, $\tau =\omega _{n}t$ is the dimensionless time, $\omega _{n}=\frac{k_{1}}{M}$ is natural frequency of linear system, $\beta =\frac{k_{2}}{k_{1}}$ is the stiffness ratio, $e=\frac{g}{y_{0}}$ is the dimensionless gap between equilibrium of mass M and the stop suspended on the spring $k_{2}$, $a=\frac{A}{y_{0}}$ and $\omega =\frac{\Omega }{\omega _{n}}$ are dimensionless amplitude and frequency of excitation, $\xi =\frac{c}{2m\omega _{n}}$ is the damping ratio and $\hbox {H}(\cdot )$ is the Heaviside function. In our calculations we take the following values of system’s parameters: $a=0.7$, $\xi =0.01$, $\beta =29$ and $e=1.26$. As a controlling parameter we use frequency of excitation $\omega$.

3.2.1 Results

3.2.2 Duffing System with Suspended Pendulum

At the beginning, we want to recall the results we have presented in our previous paper [13]. As a summary we show two dimensional bifurcation diagram obtained by path-following method in Fig. 2. It shows bifurcations for varying amplitude f and frequency $\omega$ of external excitation (see Eq. 2). Lines shown in the plot correspond to different types of bifurcations (period doubling, symmetry breaking, Neimark–Sacker) and resonance tongues. The main difference between solutions is the behaviour of pendulum, hence we introduce the notion which let us distinguish them. The Duffing system follows the excitations, while pendulum oscillates or rotates. The number of full period of pendulum motion differs for one period of excitation. To define it, we introduce the ratio u:z which gives information how many periods of excitation u are performed for z number of pendulum oscillations or rotations (the period of given solution corresponds to u multiply by period of excitation). We present these lines in one style because the structure is too complex to follow bifurcation scenarios and we do not need that data (details are shown in [13]). We mark areas where we observe the coexistence of one (black colour), two (grey colour) and three (hatched area) stable solutions. The remaining part of the diagram (white area) corresponds to situation where there are four or more solutions simultaneously. Additionally, by white colour we also mark areas where only Duffing system is oscillating in 1:1 resonance with frequency of excitation and the pendulum is in stable equilibrium position, i.e., hanging down pendulum (HDP) state. In this case the dynamics of the system is reduced to the oscillations of summary mass ($M+m$). As we can see, the range where less than three solutions exist is rather small.

The detailed analysis of the system given by Eq. 2 is time consuming and creation of Fig. 2 was preceded by complex analysis done with large computational effort. Additionally, the obtained results do not give us information about the size of basins of attraction of each solution and their stability margins. Thus, using the path-following analysis we can obtain detailed bifurcation structure of system but cannot assess which solutions are practically accessible and are expected to occur in the real system. For example some solutions may need initial conditions which are not accessible in practice (too large displacement or velocity) or have minimal stability margin such that even small perturbation may cause the jump into another attractor. We will present that sample based analysis serves greatly for that purpose. For illustrative purposes we focus on three solutions: 2:1 oscillating resonance, HDP and 1:1 rotating resonance assuming that only they have practical meaning.

Fig. 2

Two-parameter bifurcations diagram in plane $\left( f,\,\omega \right)$ showing periodic oscillations and rotations of pendulum. Black colour indicates one attractor, grey colour shows two coexisting attractors (the same as for black but with coexisting stable steady state of the pendulum). In the hatched area we observe the coexistence of stable rotations and stable steady state of the pendulum. Figure reprinted from [12]. Detailed analysis can be found in [13]

Firstly, we show reference results obtained with direct numerical integration. These are two bifurcation diagrams calculated for constant amplitude of excitation $f=0.5$ and frequency from the range $\omega \in [0.1,\;3.0]$ (see Fig. 3). In Fig. 3a we increase excitation frequency $\omega$ from 0.1 to 3.0 and in subplot (b) we decrease $\omega$ from 3.0 to 0.1. As the initial conditions for the first points of the bifurcation diagrams we take equilibrium position $(x_{0}={\dot{x}}_{0}=0.0$ and $\varphi _{0}={\dot{\varphi }}_{0}=0.0)$. In both panels we plot amplitude of pendulum $\varphi$ which reflects the type of attractor. In the considered range there are two dominating solutions: HDP and 2:1 internal resonance. Near $\omega =1.0$ we observe a narrow range of 1:1 and 9:9 resonances and chaotic motion (for details see Fig. 6 in [13]). Ranges where diagrams differ are marked with grey rectangles. Based on previous results we know that we detect all solutions existing in the considered range, however we do not have data about size of their basins of attraction and coexistence. Hence, the analysis with proposed method should give us new important information about system’s dynamics. Contrary to bifurcation diagram obtained by path-following presented in Fig. 3 we do not observe a rotating solutions (the other set of initial conditions should be taken). This shows the main disadvantage of classical bifurcation diagrams.

Fig. 3

Bifurcation diagrams obtained using direct numerical integration. For subplot (a) value of bifurcation parameter $\omega$ was increased while for subplot (b) we decreased value of $\omega$. Gray rectangles mark the ranges of bifurcation parameter $\omega$ for which different attractors coexist. Figure reprinted from [12]

Now, we apply the sample based analysis. The initial conditions are random numbers drawn from the following ranges: $x_{0}\in [-\,2,\,2]$, ${\dot{x}}_{0}\in [-\,2,\,2]$, $\varphi _{0}\in [-\,\pi ,\,\pi ]$ and ${\dot{\varphi }}_{0}\in [-\,2.0,\,2.0]$ (ranges there selected basing on the results from [13]). Frequency of excitation is within range $\omega \in (0.0,\,3.0]$ (Fig. 4a, c), then to have a zoom in narrower range, we refine it to $\omega \in [1.25,\,2.75]$ (Fig. 4b, d). In both cases we take 15 equally spaced subsets of $\omega$ and in each subset we calculate the probability of reaching given solution. For each subset we calculate $N=1000$ trials each time drawing initial conditions of the system and value of $\omega$ from the appropriate range. Then we plot the dot in the middle of the subset which indicate the probability of reaching given solution in each considered range. Lines that connect the dots are marked just to show the tendency. For each range we take $N=1000$ because we want to estimate the probability of solution with small basin of stability (1:1 rotating periodic solution).

In Fig. 4 we show the probability of reaching three aforementioned solutions obtained using the proposed method. In Fig. 2 we see that the 2:1 resonance solution exists in the area marked by black colour around $\omega =2.0$ and coexists with HDP in neighbouring grey zone. In Fig. 4 we mark the probability of reaching 2:1 resonance (p(2:1) ) using blue dots. As we expect for $\omega <1.4$ and $\omega >2.2$ the solution does not exist. In the range $\omega \in [1.4,\,2.2]$ the maximum value of probability $p(2:1)=0.971$ is reached in the subset $\omega \in [1.8,\,2.0]$ and outside that range the probability decreases significantly. To check if we can reach $p(2{:}1)=1.0$ (so that it is the only stable attractor) we decrease the range of parameter’s values to $\omega \in [1.25,\,2.75]$ and the size of subset to $\Delta \omega =0.1$ (to remain with 15 equally spaced subsets). The results are shown in Fig. 4b using blue colour. In the range $\omega \in [1.95,\,2.05]$ the probability p(2:1) is equal to unity and in range $\omega \in [1.85,\,1.95]$ it is slightly smaller $p(2{:}1)=0.992$. Hence, for both subsets we can be nearly sure that system reaches 2:1 solution. This gives us indication of how precise we have to set the value of $\omega$ to be sure that the system will behave in a presumed way. This has practical importance and can be used when designing the system which cannot be multistable.

The similar analysis is performed for HDP solution. The values of probability are reflected using red dots on the same plots in Fig. 4. For $\omega \le 0.8$, $\omega \in [1.2,\,1.4]$ and $\omega \in [2.6,\,2.8]$ the HDP is the only existing solution. The rapid decrease close to $\omega \approx 1.0$ indicate the 1:1 resonance and the presence of other coexisting solutions in this range (see [13]). In the range $\omega \in [1.2,\,1.4]$ the basin stability of HDP solution is a unity ($p({\mathrm {HDP}})=1.0$) which corresponds to a border between solutions born from 1:1 and 2:1 resonance. Hence, up to $\omega =2.0$ the probability of HDP solution is a mirror refection of p(2:1). The same tendency is observed in the narrowed range as presented in Fig. 4b. Finally, for $\omega >2.0$ the third considered solution comes in and we start to observe an increase of probability of rotating solution as shown in Fig. 4c. However, the chance of reaching rotating solution remains small and never exceeds $p({\mathrm {1:1}})=8\times 10^{-3}$. We also plot the probability of reaching rotating solution in the narrower range of $\omega$ in Fig. 4d. The probability is similar to the one presented in Fig. 4c—it is low and do not exceed $p({\mathrm {1:1}})=8\times 10^{-3}$. Note, that results presented in Fig. 4a, b and Fig. 4c, d are computed for different sets of random initial conditions and parameter values, hence the obtained probability can be slightly different. Still, it is inherent feature of the sample based methods and does not impede their advantages.

Fig. 4

Probability of reaching given solutions in the system 2. Subplots (a, b) present the probability of reaching 2:1 periodic oscillations (blue) and HDP (red). Subplots (c, d) presents the probability of reaching 1:1 rotations (black). (Please note that in both cases (a, b) and (c, d) the initial conditions and parameter are somehow random, hence the results may slightly differ). Figure reprinted from [12]. (Color figure online)

3.2.3 Bilinear Impacting Oscillator

Now, we present the analysis of the bilinear system with impacts. A discontinuity usually increases the number of coexisting solutions. Hence, in the considered system we observe a large number of different stable orbits, but we will consider only periodic solutions of different periods. In Fig. 5 we show two bifurcation diagrams with $\omega$ as controlling parameter. Both of them are obtained by starting with zero initial conditions $x_{0}=0.0$ and ${\dot{x}}_{0}=0.0$. In panel (a) we increase $\omega$ from 0.801 to 0.8075; while in panel (b) we decrease $\omega$ in the same range. We select the range of $\omega$ basing on the results presented in [72]. As one can see, both diagrams differ in two zones marked by grey colour. Hence, we observe a coexistence of different solutions, i.e., in the range $\omega \in [0.8033,\,0.8044]$ solutions with period-3 and -2 are present, while in the range $\omega \in [0.8068,\,0.8075]$ we detected solutions with period-2 and -5 (numbers indicate how many times the period of solution is longer then the period of excitation). As presented in [72], some solutions appear from a saddle-node bifurcation and we are not able to detect them with the classical bifurcation diagram. The proposed method solves this problem and shows all existing solutions in the considered range of excitation frequency.

Fig. 5

Bifurcation diagram showing the behaviour of impacting oscillator (see Eq. 3). Subplot a for increasing value of the bifurcation parameter $\omega$ and b for decreasing the value of $\omega$. Grey rectangles mark the range of the bifurcation parameter $\omega$ for which different attractors coexist. Figure reprinted from [12]. Further analysis can be found in [72]

We focus on periodic solutions with periods that are not longer than eight periods of excitation. Solutions with higher periods are observed in the narrow range of $\omega$ but the probability that they will occur is very small so they can be neglected. All non-periodic solutions are chaotic (quasiperiodic solutions are not present in this system). The results of our calculations are shown in Fig. 6a, b. We take initial conditions from the following ranges $x_{0}\in [-\,2,\,2]$, ${\dot{x}}_{0}\in [-\,2,\,2]$. The controlling parameter $\omega$ is changed from 0.801 to 0.8075 with step $\Delta \omega =0.0005$ in Fig. 6a and from 0.806 to 0.8075 with the step $\Delta \omega =0.0001$ in Fig. 6b. In each subrange of excitation’s frequency we pick the exact value of $\omega$ randomly from this subset, as described earlier. The probability of reaching periodic solutions is plotted with lines of different colours that are created by joining markers that reflect probability obtained for given range of $\omega$. The solutions of different periods were detected and investigated, namely solutions with period-1, -2, -3, -5 (two different attractors with large and small amplitude), -6 and -8. We also calculate the sum of reaching one of all periodic solutions’ (also with period higher then eight). It is plotted with yellow markers and lines. When its value is below 1, chaotic solution exists. Dots are drawn for mean value i.e, middle of the subset. For each range we take $N=200$ and we increase the calculation time because the transient time is sufficiently larger than in the previous example due to the piecewise smooth characteristic of spring’s stiffness.

As we can see, the chance of reaching a given solution strongly depends on $\omega$. Hence, in the sense of basin stability we can say that $\omega$ value strongly affects stability of attractors. In Fig. 6a the probability of a single solution is always smaller than one. Nevertheless, there are two dominant solutions: period-5 with large amplitude in the first half of the considered $\omega$ range and period-2 in the second half of the range. The maximum registered value of probability is $p({\mathrm {period-2}})=0.92$ and it refers to the period-2 solution for $\omega \approx 0.80675$. To check if we can achieve even higher probability we analyse a narrower range of $\omega$ and decrease the range from which we draw $\omega$ value (from $\Delta \omega =0.0005$ to $\Delta \omega =0.0001$). In Fig. 6b we see that in range $\omega \in [0.8069,\,0.807]$ the probability of reaching the period-2 solution is equal to unity. Hence, in the sense of basin stability it is the only stable solution. In the range $\omega \in [0.8065,\,0.8072]$ the probability of reaching this solution is higher then 0.9 and we can say that its basin of attraction is strongly dominant. Hence, the obtained results give the required tolerance of $\omega$ to omit multistability and be sure that period-2 solution will be observed. This proves the practical importance of the method.

Other periodic solutions presented in Fig. 6a are: period-1 is present in the range $\omega \in [0.801,\,0.8025]$ with the highest probability $p({\mathrm {period-1}})=0.4$, period-3 exists in the range $\omega \in [0.803,\,0.805]$ with the maximum probability $p({\mathrm {period-3}})=0.36$, period-2 is observed in two ranges $\omega \in [0.8025,\,0.8035]$ and $\omega \in [0.804,\,0.8045]$ with the highest probability equal to 0.18 and 0.12 respectively. Solution with period-5 (small amplitude’s attractor) exists also in two ranges $\omega \in [0.8055,\,0.8065]$ and $\omega \in [0.807,\,0.8075]$ with the highest probability equal to 0.14 and 0.43 respectively.

Fig. 6

Probability of reaching periodic solutions in the bilinear impacting oscillator 3 (a, b) and relative basins volume (c, d). In Subplots (a, c) we analyze $\omega \in [0.801,\,0.8075]$ with the step $\Delta \omega =0.0005$, and in subplots (b, d) we narrow the range $\omega \in [0.806,\,0.8075]$ and decrease the step size $\Delta \omega =0.0001$. (Note that initial conditions and parameter are somehow random, hence the results may slightly differ)

The same information can be also presented using the relative basin volume plots as shown in panels (c, d) in Fig. 6. Such plots are predisposed for presentation when we consider multiple solutions as they enable easy comparison between basins volume and make presentation more readable when many solutions have similar basin probability measure.

3.3 Practical Application

Now, we will present an example of practical application of the above technique basing on the hybrid dynamical model of the yoke-bell-clapper system. The model was validated experimentally [11] and thoroughly analysed using classical methods including direct numerical integration [10] and path-following [9, 16]. The model possess a plethora of interesting dynamical phenomena including multistability [9, 16] and new type of bifurcation called “impact adding bifurcation” [9]. This system is highly predisposed to sample analysis because in most cases we cannot determine parameter values with good precision. It is due to the fact that bellfounding (casting of bells) is still based more on traditional methods and local customs than engineering science. Similarly, when designing the yoke and propulsion one does not have the precise knowledge about the shape of the bell and clapper. Thus, we usually observe some imperfections and the real system is just a rough embodiment of the assumed design. This problem can be partly solved with the sample based analysis, in which we can introduce parameters mismatch and find ranges of crucial parameter values which guarantees the highest probability that the system will work properly.

The investigated model is based on the existing bell “The Heart of Lodz” of the Cathedral Basilica of St Stanislaus Kostka, Lodz, Poland and all parameters values were obtained in a series of dedicated experiments [10, 11]. The derivation of the model is described in detail in [11] and now we just briefly recall it. The developed mathematical model is based on the analogy between freely swinging bell and the motion of the equivalent double physical pendulum. The first pendulum has fixed axis of rotation and models the yoke together with the bell that is mounted on it. The second pendulum is attached to the first one and imitates the clapper. Figure 7a, b show schematics indicating the position of the rotation axes of the bell $o_{1}$, the clapper $o_{2}$ and presenting parameters involved in the model. For the sake of simplicity, henceforth, the term “bell” is used for the bell and its yoke, which is treated as one solid element.

Fig. 7

Schematics of the physical model of the yoke-bell-clapper system in different planes to show its geometry, kinematics and physical parameters

The model has eight physical parameters: $L_{0}$ describes the distance between the rotation axis of the bell and its centre of gravity (point $C_{b}$), l is the distance between the rotation axis of the clapper and its centre of gravity (point $C_{c}$). The distance between the bell’s and the clapper’s axes of rotation is given by $l_{c0}$. The mass of the bell is described by M, while $B_{b0}$ characterizes the bell’s moment of inertia referred to its axis of rotation. Similarly, m describes the mass of the clapper and $B_{c}$ stands for the clapper’s moment of inertia referred to its axis of rotation.

We have to remember that we consider a musical instrument, hence we cannot change most of its parameters as it could affect the sound it generates. In real applications we can easily modify the driving motor and the mounting of the bell (by changing the design of the yoke). Therefore, in our investigation we will consider alterations of these two features taking as a reference parameter values that refer to “The Heart of Lodz”.

Parameter $l_{r}$ is used to describe the modifications of the yoke, as it is presented in Fig. 7b, c. The $l_{r}$ definition is explained in detail in our previous paper [10], where $l_{r}=0$ refers to the shape of original yoke used in the Cathedral’s Basilica bell. If the centre bell’s of gravity is lowered with respect to its axis of rotation, $l_{r}<0$, otherwise $l_{r}>0$. The change of the yoke design given by the value of $l_{r}$ affects other parameters. Therefore, in the mathematical model, the following parameters that describe the system with the modified yoke are used:

$$\begin{aligned} L=L_{0}-l_{r}, \quad l_{c}=l_{c0}-l_{r}, \quad B_{b}=\left( B_{b0}-ML_{0}^{2}\right) +ML^{2}. \end{aligned}$$

(4)

The bell is excited with a linear motor. When the deflection of the yoke is smaller than $\pi /15\,[\hbox {rad}]$$(12^{\circ })$ the motor is active and generates the torque. The torque generated by the motor $T(\varphi _{1})$ is given by the piecewise formula:

$$(\varphi _{1} ) = \left\{ {\begin{aligned} {\begin{array}{*{20}c} {T_{{max}} {\mkern 1mu} {\text{sgn}}(\dot{\varphi }_{1} ){\mkern 1mu} \cos \left( {7.5\varphi _{1} } \right),} & {if} & {|\varphi _{1} | \le \frac{\pi }{{15}}} \\ {0,} & {if} & {|\varphi _{1} | > \frac{\pi }{{15}}} \\ \end{array} } \hfill \\ \end{aligned} } \right.$$

(5)

where $T_{max}$ is the maximum torque. Although, the above expression is not fully accurate reflection of the effects generated by the linear motor it is able to reproduce the characteristics of the modern bells’ driving mechanisms [11]. We can easily modify the effects generated by the motor by changing the range of bell’s deflection in which the motor is active (in our case $\left[ -\pi /15,\,\pi /15\right]$) or by altering the maximum generated torque $T_{max}$ which is much easier to realize in practice [10]. Therefore, we take $T_{max}$ as the second control parameter.

As shown in Fig. 7a we use a planar co-ordinate system where the angle between the bell’s axis and the downward vertical is given by $\varphi _{1}$ and the angle between the clapper’s axis and downward vertical by $\varphi _{2}$. Angular parameter $\alpha$ describes the impact condition as follow:

$$\begin{aligned} |\varphi _{1}-\varphi _{2}|=\alpha . \end{aligned}$$

(6)

Synonymously, contact between the bell and the clapper occurs when a relative angular displacement between the bell and the clapper is equal to $\alpha$.

The Lagrange equations of the second type are employed to derive two coupled second order ODEs that describe the motion of the system:

$$\begin{aligned}&\left( B_{b}+ml_{c}^{2}\right) \ddot{\varphi }_{1}+ml_{c}l\ddot{\varphi }_{2}\cos \left( \varphi _{2}-\varphi _{1}\right) -ml_{c}l{\dot{\varphi }}_{2}^{2}\sin \left( \varphi _{2}-\varphi _{1}\right) \nonumber \\&\quad +\left( ML+ml_{c}\right) g\sin \varphi _{1}+D_{b}{\dot{\varphi }}_{1}-D_{c}\left( {\dot{\varphi }}_{2}-{\dot{\varphi }}_{1}\right) =T(\varphi _{1}), \end{aligned}$$

(7)

$$\begin{aligned}&B_{c}\ddot{\varphi }_{2}+ml_{c}l\ddot{\varphi }_{1}\cos \left( \varphi _{2}-\varphi _{1}\right) +ml_{c}l{\dot{\varphi }}_{1}^{2}\sin \left( \varphi _{2}-\varphi _{1}\right) +mgl\sin \varphi _{2}+D_{c}\left( {\dot{\varphi }}_{2}-{\dot{\varphi }}_{1}\right) =0, \end{aligned}$$

(8)

where g stands for gravity.

We use a discreet impact model. If Eq. 6 is fulfilled, the numerical integration process is paused. Then, simulation is restarted with updated initial conditions. The bell’s and the clapper’s angular velocities are swapped from the values before the impact to the ones after the impact. The angular velocities after the impact are obtained by taking into account the energy dissipation and the conservation of the system’s angular momentum that are expressed by the following formulas:

$$\begin{aligned}&\frac{1}{2}B_{c}\left( {\dot{\varphi }}_{2,AI}-{\dot{\varphi }}_{1,AI}\right) ^{2}=k\frac{1}{2}B_{c}\left( {\dot{\varphi }}_{2,BI}-{\dot{\varphi }}_{1,BI}\right) ^{2}, \end{aligned}$$

(9)

$$\begin{aligned}&\left[ B_{b}+ml_{c}^{2}+ml_{c}l\cos \left( \varphi _{2}-\varphi _{1}\right) \right] {\dot{\varphi }}_{1,BI}+\left[ B_{c}\right. \nonumber \\&\left. \quad +ml_{c}l\cos \left( \varphi _{2}-\varphi _{1}\right) \right] {\dot{\varphi }}_{2,BI}\nonumber \\&=\left[ B_{b}+ml_{c}^{2}+ml_{c}l\cos \left( \varphi _{2}-\varphi _{1}\right) \right] {\dot{\varphi }}_{1,AI}\nonumber \\&\quad +\left[ B_{c}+ml_{c}l\cos \left( \varphi _{2}-\varphi _{1}\right) \right] {\dot{\varphi }}_{2,AI} \end{aligned}$$

(10)

where index AI stands for “after impact”, index BI for “before impact” and parameter k is the coefficient of energy restitution and in our simulations we assume $k=0.05\,[-]$ [11]. Eqs 7 and 8 together with the impact model create a hybrid dynamical system.

The mathematical model contains eleven physical parameters which values were derived experimentally in a series of dedicated experiments. Their values are the following: $M=2633$ [kg], $m=57.4$ [kg], $B_{b0}=1375\,[\hbox {kgm}^{2}]$, $B_{c}=45.15\,[\hbox {kgm}^{2}]$, $L_{0}=0.236$ [m], $l=0.739$ [m], $l_{c0}=-\,0.1$ [m] and $\alpha =30.65^{\circ }=0.5349$ [rad], $D_{c}=4.539$ [Nms], $D_{b}=26.68$ [Nms] and we consider the control parameters from the following ranges: $T_{max}\in [100,\,650]$ [Nm] and $l_{r}\in [-\,1.3,\,0.25]$ [m].

3.3.1 Results

Depending on local customs and traditions bells can have different working regimes. We can alter them easily by changing the design of yoke and/or propulsion [10]. Still, for some values of parameters the system is multistable and the final attractor depends on initial conditions or starting procedure. Moreover, as mentioned before, the final object is often a rough realization of initial concept, and we cannot predict the actual values of system parameters before it is build. Thus, instead of analyzing the dynamics for some fixed values we can apply the sample based approach. Including some parameters mismatch we can estimate the ranges of parameters that ensure proper working conditions and define the precision required to achieve mandatory level of reliability. As a reference we use the results presented in [9] where we consider alteration of the yoke design given by parameter $l_{r}$. As a reference we use “The Heart of Lodz” which works in “symmetric falling clapper” regime (collisions between the bell and the clapper occur when they perform an anti-phase motion). We consider the range of parameter $l_{r}\in [-\,0.3,\,0.2]$ [m] in which we observe 13 different types of attractors and multistable regions. The detailed description of all considered solutions is given in [9], where we also present in depth analysis done using the path-following method [20] and direct numerical integration. The obtained results enable to detect the ranges where we presume that there is only one stable attractor. Moreover, for multistable regions we do not have the knowledge about the chances of reaching given solution and structure and size its of basins of attraction. To obtain such information we apply the sample based analysis described above.

We divide the investigated range of $l_{r}\in [-\,0.3,\,0.2]$ [m] into 50 subranges of equal length 0.01 [m] which reflects the maximum expected precision of assembly. For each subset we perform 40,000 trials of direct numerical integration each time drawing the values of $l_{r}$ and initial conditions from accessible ranges which are assumed as follows:

$$\begin{aligned} \varphi _{1_{0}}\in [-\,\pi ,\,\pi ]\,[\hbox {rad}],\nonumber \\ \varphi _{2_{0}}\in [-\,\pi ,\,\pi ]\,[\hbox {rad}],\nonumber \\ {\dot{\varphi }}_{1_{0}}\in [-\,\pi /2,\,\pi /2]\,[\hbox {rad}/\hbox {s}],\nonumber \\ {\dot{\varphi }}_{2_{0}}\in [-\,\pi ,\,\pi ]\,[\hbox {rad}/\hbox {s}], \end{aligned}$$

(11)

additionally condition that ensures that clapper is inside the bell $\left| \varphi _{1_{0}}-\varphi _{2_{0}}\right| \le \alpha$ must be fulfilled. Then, for each trial we detect the final attractor and estimate probability of reaching given solution in each considered range. The results are shown in Fig. 8. In panel (a) we present the bifurcation diagram obtained using multiple trials of direct numerical integration (it was previously shown and described in [9]). In panel (b) we show how the probability of reaching given solution depends on the value of $l_{r}$. Finally, in panel (c) we present the relative volume of basins of attraction.

Fig. 8

Bifurcation diagram (a) shows possible responses of the yoke-bell-clapper system and outcomes of the sample based analysis (b, c). Panel (b) shows the changes in probability of reaching given solution and panel (c) the changes of relative basin volume. Considered solutions and corresponding colours are given in the table at the bottom. Numbers (nos) of solutions correspond to the notation used in [9]. (Color figure online)

All considered solutions are given in the table at the bottom of Fig. 8. Analysing the plots we see that in the range $l_{r}\in \left[ -\,0.09,\,0.13\right]$ [m] solution 8 has the dominant volume and the basin stability measure greater than 0.8. This solution corresponds to the original working regime of “The Heart of Lodz” and has the largest range of stability. The second larges range of stability refers to solutions 6 and 7 which are two types of “asymmetric falling clapper” and are another type of proper working regime (the impact occurs only on one side of the bell). Solutions 2, 3, 4 and 5 are all periodic with different number of impacts per period of motion. Moreover, for solutions 3, 4 and 5 we can define the range in which they have basin stability greater than 0.98, so theoretically, they can be applied in the real system and assure reliable operation. Solution 1 refers to periodic oscillations without impacts, hence we should omit it similarly as all non periodic solutions depicted in panel (c) with grey colour. In the righthand side of the plot we see the sequence of impact adding bifurcations in which solutions 9, 10 and 11with different number of impacts are created. However only solution 9 have basin stability greater then 0.96 in the range $l_{r}\in \left[ 0.14,\,0.16\right]$ [m] and can be realized in practice. Finally, for $l_{r}>0.17$ [m] solution 12, which corresponds to the “sticking clapper” regime (working regime in which the clapper and the bell remain in contact for a certain amount of time), has the dominant basin. Summarizing, the sample based analysis presented above enables to detect the ranges of parameter values that ensure predictable behavior and reliable operation.

4 Analysis of Multistability

There is a rich variety of mathematical tools to analyze multistable dynamical systems. Still, more sophisticated methods are usually difficult to apply. For example, there are a number of different toolboxes that enable the path-following analysis but their functionality is strictly limited to the type of the investigated system and its dimensionality [25, 28, 90]. The dynamical analysis is especially challenging for multistable systems, where we have to consider multiple steady states that coexist in the phase space. It is a challenging problem and multistability is widely studied in many disciplines [26, 38, 58, 59, 75, 84, 88, 94]. Therefore, new sample based tools for dynamical analysis are being developed such as survivability [36] that includes the analysis of the transient motion and basin entropy [22] that measures the basin compactness. The concept presented in the previous Section is also suitable for investigation of multiple coexisting attractors. Moreover, it enables to perform simultaneous analysis in a multi-parameter space. In this Section we will show analysis in two-parameter space and compare the results from sample-based analysis with detailed two parameter bifurcation diagrams obtained using the path-following method. Then, to validate the method we confront the results with experimental data. By that we are able to critically compare the accuracy of both methods and show their strengths and weaknesses. Finally, we show that the sample-based approach can be applied without a precise knowledge of parameter values and it gives results that can be used in practice.

4.1 Investigated System

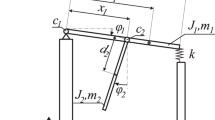
We consider the specific type of a double pendulum (see Fig. 9) which is a paradigmatic example in nonlinear dynamics. The first pendulum rod is mounted horizontally and connected to the base with a pin joint at one end and via a spring on the second end. Hence, the first pendulum always performs oscillatory motion. The second pendulum is connected to the first one with a rotational pivot at the distance $x_{1}$ between both pin joints. The support is mounted on a shaker and excited kinematically in the vertical direction. This is a physical model of the existing experimental rig shown in the photographic picture in Fig. 9b. The dynamics of this system was analysed in the recent article [15].

The system has two degrees of freedom. The angular displacement of the first pendulum is given by generalized coordinate $\varphi _{1}$ and the position of the second pendulum by $\varphi _{2}$. The shaker excites the system kinematically with a harmonic function of the amplitude A and frequency $\omega$. The upper pendulum has the length $l_{1}$, the mass $m_{1}$, the moment of inertia $J_{1}$ and the centre of gravity located at the distance $d_{1}$ from its pin joint. The stiffness of the spring that supports the end of the pendulum is given by k. The second pendulum has the mass $m_{2}$, the moment of inertia $J_{2}$ and the center of gravity located at $d_{2}$ from its pin joint. Due to the relatively small damping in the system we neglect effects of dry friction and other non-linearities of damping characteristics and in both pivots we assume the viscoelastic damping. For the first pendulum the damping coefficient is given by $c_{1}$ and for the second one by $c_{2}$.

Fig. 9

The physical model of the considered double pendulum excited kinematically (Eq. 12) with its parameters

The equations of motion of the system shown in Fig. 9 are given by the following second order ODEs:

$$\begin{aligned}&\left( J_{2}+m_{2}d_{2}^{2}\right) \ddot{\varphi }_{2}+m_{2}d_{2}\left( A\omega ^{2}\cos (\omega t)+g\right) \sin \varphi _{2}\nonumber \\&\qquad +\,m_{2}d_{2}\left( x_{1}\left( \cos \left( \varphi _{1}-\varphi _{2}\right) {\dot{\varphi }}_{1}^{2}+\sin \left( \varphi _{1}-\varphi _{2}\right) \ddot{\varphi }_{1}\right) \right) +c_{2}{\dot{\varphi }}_{2}=0, \nonumber \\&\quad \left( J_{1}+m_{1}d_{1}^{2}+m_{2}x_{1}^{2}\right) \ddot{\varphi }_{1}+c_{1}{\dot{\varphi }}_{1}+\frac{1}{2}l_{1}^{2}k\sin \left( 2\varphi _{1}\right) \nonumber \\&\qquad +\,m_{2}x_{1}d_{2}\left( \sin \left( \varphi _{1}-\varphi _{2}\right) \ddot{\varphi }_{2}-\cos \left( \varphi _{1}-\varphi _{2}\right) {\dot{\varphi }}_{2}^{2}\right) \nonumber \\&\qquad -\,\left( m_{1}d_{1}+m_{2}x_{1}\right) \left( A\omega ^{2}\cos (\omega t)+g\right) \cos \varphi _{1}=0. \end{aligned}$$

(12)

The parameters have the following values: $J_{1}=4.524\,[{\mathrm {10^{-3}\,kgm^{2}}}]$, $m_{1}=0.5562\,[{\mathrm {kg}}]$, $l_{1}=0.315\,[{\mathrm {m}}]$, $d_{1}=0.180\,[{\mathrm {m}}]$, $x_{1}=0.153\,[{\mathrm {m}}]$, $c_{1}=0.05\,[{\mathrm {Nms}}]$, $k=6850\,[{\mathrm {N/m}}]$, $J_{2}=4.469\,[{\mathrm {10^{-5}\,kgm^{2}}}]$, $m_{2}=0.02077\,[{\mathrm {kg}}]$, $d_{2}=0.063\,[{\mathrm {m}}]$, $c_{1}=7\,[{\mathrm {10^{-6}\,Nms}}]$, $g=9.81\,[{\mathrm {m/s^{2}}}]$. All the parameter values were determined in a series of dedicated experiments. Thanks to the shaker the amplitude and frequency of excitation can be changed in the following ranges $A\in \left[ 0,\,0.0077\right] \,[{\mathrm {m}}]$ and $\omega \in \left[ 0,\,60\right] \,[{\mathrm {rad/s}}]$. These ranges are defined by the limitations of the experimental rig, higher amplitudes of the shaker are impossible to achieve and for higher values of frequencies the accessible amplitude of the excitation $A_{max}$ is rapidly dropping.

We have to estimate the ranges of initial conditions that can be applied on our experimental rig. In a number of dedicated experiments we defined the accessible ranges of initial conditions that describe physical restrictions of our rig: $\varphi _{1}\epsilon \left[ -\,0.0015,\,0.0015\right] \,[{\mathrm {rad}}]$, $\varphi _{2}\epsilon \left[ -\,\pi ,\,\pi \right] \,[{\mathrm {rad}}]$, ${\dot{\varphi }}_{1}\epsilon [-\,1.2,\,1.2]\,[{\mathrm {rad/s}}]$, ${\dot{\varphi }}_{2}\epsilon [-\,60,\,60]\,[{\mathrm {rad/s}}]$. Then, we divide the considered ranges of parameter values into a regular two dimensional grid in the following way: for the frequency of excitation ($\omega \epsilon [0,\,60]\,[{\mathrm {rad/s}}]$) we assume 23 subsets with equal width of $2.5\,[{\mathrm {rad/s}}]$. We intentionally omit extremely small values of $\omega$ and start from the range$\left[ 1.25,\,3.75\right] \,[{\mathrm {rad/s}}]$ (for first column of the grid) and finish with $\left[ 56.25,\,58.75\right] \,[{\mathrm {rad/s}}]$ (for the last column). For the amplitude of forcing $A\epsilon \left[ 0,\,7.7\right] \,[10^{-3}{\mathrm {m}}]$ we take 15 equally spaced subsets with the step of $0.5\,[10^{-3}{\mathrm {m}}]$. Here, we also ignore values near the accessible boundaries and start the lower row of the grid with the range of $\left[ 0.25,\,0.75\right] \,[10^{-3}{\mathrm {m}}]$ and finish the grid with $\left[ 7.25,\,7.75\right] \,[10^{-3}{\mathrm {m}}]$. By that, we receive a lattice of 345 boxes each covering the range of $2.5\,[{\mathrm {rad/s}}]$ and $0.5\,[10^{-3}{\mathrm {m}}]$ of the forcing frequencies and amplitudes respectively. For each box in the grid we perform 500 trials of direct numerical integration. Each time we randomly pick the initial conditions from the accessible ranges and draw the values of A and $\omega$ from the ranges assigned to the grid box. For every trial we recognize the final attractor that is reached by the system. In a procedure described above, we obtain a large data set of 172, 500 Bernoulli trials that we use to characterize the possible behaviors of the system.

4.2 Methodology

We investigate the ranges of stability of coexisting solutions in two-parameters space using two different approaches and validate them with experiments. We start with the path-following method to get a precise boundaries of solutions’ stability in two-parameters. The path-following analysis is done with the AUTO-07p software [24]. Each time we start with a direct numerical integration to prepare the initial periodic solution for continuation. Then, we perform with one parameter continuation in selected parameter. We detect the bifurcation points in which the stability of solution changes and perform continuation of the bifurcation points in two parameters space. For the solutions detected numerically, we experimentally find the boundaries of the stability similarly in the two parameter space (here we use the amplitude and frequency of excitation A and $\omega$, respectively).

Then, for each solution we perform experiments to assess the stability ranges. The starting points for the experimental study are located far from the boundary of stability to ensure that the given solution is reachable experimentally. Depending on the shape and area of the stability range, we select a number of starting points and for each apply the following procedure:

• We start the parameter values taken from numerical results and try to reach the given solution by applying proper initial conditions.

• When the system reaches the presumed state we mark current parameters values as a starting point (black dots in Fig. 10) in the two parameter space.

• Then, we slowly change the value of one parameter with given step. After each step we wait to check if the system remains on the presumed attractor. The range of the parameter value where the solution stays stable is marked as a trace with a black line in Fig. 10d, e.

• Eventually, we reach the parameter value for which the solution becomes unstable and the system jumps to a different attractor. We note the parameter value for which the solution changed.

• In each case we repeat the above steps four times and compute the average values of parameters for which the solution looses its stability. We take this value as the boundary of stability and mark it with the perpendicular end of the stability trace (see Fig. 10d, e).

To estimate the position of a line that indicates the boundary of stability obtained by the path-following method in the two parameter space, we repeat the above procedure for different pairs of parameters values (starting points).

Finally, we apply the sample-based approach (as described in Sect. 3) to determine the ranges of parameters for which the given solution can be reached. We divide the considered ranges of parameter values into a regular two dimensional grid. For each box in the grid we perform N trials of direct numerical integration. Each time we randomly pick the initial conditions from the accessible ranges and draw the values of investigated parameters from the ranges assigned to the grid box. For every trial we recognize the final attractor that is reached by the system. The data enable us to estimate the ranges of stability for each considered attractor. For that purpose, we detect all the trajectories that go to the investigated attractor and mark the parameters value (A and $\omega$) for which it has been approached. Then, we plot those values as a set of points that indicates the region of stability of the investigated solution. Apart from that, the collected data enable us to calculate the maps of basin stability in the two parameter space, as shown in Fig. 10c and f where we show the probability of occurrence of the considered solution.

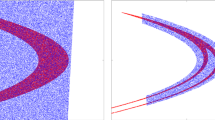
In Fig. 10 we show the presentation scheme that we use. It enables to show all of the obtained results and ensures an easy comparison between the methods. In Fig. 10 we present the results yielded for some exemplary solution (1:2 oscillations of system given by equations 12) and explain the presentation layout. Arrows in Fig. 10 show how the data are interchanged between the panels.

We start with the path-following method. We begin with one parameter continuation performed to detect the bifurcation points in which the stability of the solution changes. These results are not presented but we use these points to perform two parameter continuation. The sample results are shown in panel (a) where lines depict bifurcations and the region of stability is marked with a coloured area. In panel (d) we show the results from the experimental analysis, while in panels (b), (c) and (f) we present the outcome of the sample-based approach. In panel (b) we plot a single colour dot (here purple) each time the investigated solution is reached in a trial. The extended basin stability approach provides a basin stability map shown in panel (c). Such plot enables to detect where the solution is more likely to appear due to the increased basin stability. It is possible to obtain 2D density plots without the grid as shown in panel (c). Such diagram enables better estimation of the stability boundaries and allows to find exact parameter values for which the probability of reaching given solution achieves extreme value.

To simplify the comparison between the results obtained with different approaches, we combine the results from panels (a), (b) and (d) in a single plot as shown in panel (e) in Fig. 10. However, the maps of basin stability provide an additional knowledge about the attractor stability. Hence, for each solution we present three diagrams corresponding to panels (c), (e) and (f). To underline this fact these three panels are surrounded with a dashed line.

Fig. 10

Presentation scheme for the stability analysis performed using different methods for 1:2 oscillatory solution of system 12. Panel (a) was obtained from the continuation of a periodic solution, in b, c, f the results obtained with a sample-based method and in d we present experimental data. In subplot (e) we compare the three numerical approaches. Line types in a indicate the following bifurcations: continuous line—saddle node, dashed line—period doubling, dotted line—symmetry breaking pitchfork and dashed-dotted line—branching point where the equilibrium destabilizes and lower pendulum starts to move

4.3 Ranges of Stability

Analyzing the ranges of stability we take as controlling parameters the amplitude A and the frequency $\omega$ of the external excitation. In the considered ranges of parameters $A\in \left[ 0,\,0.0077\right] \,[{\mathrm {m}}]$ and $\omega \in \left[ 0,\,60\right] \,[{\mathrm {rad/s}}]$ we found 12 different solutions. The upper pendulum always performs an oscillatory motion, while for the second pendulum we observe both oscillations and rotations with different locking ratios in respect to the frequency of excitation. Therefore, we name each solution basing on the behaviour of the second pendulum and ratio n:m which means that for m periods of excitation we observe n full oscillations or rotations of the second pendulum. We detected and further consider: 1:1, 1:2, 1:3, 1:4, 1:6, 1:8 oscillations, and 1:1, 1:2, 1:3, 5:5, 6:6, 2:3 rotations. The methodology of the investigation was described in Sect. 4.2 and in Fig. 11 we present the outcome from three considered methods using the described presentation scheme. The first six panels (a–f) refer to oscillatory solutions while in the last six panels we show the results corresponding to the rotary solutions.

We start the description from the oscillatory case. In panel (a) of Fig. 11 we show the results obtained for 1:1 oscillations of the second pendulum. In this solution the amplitude of oscillations is small, and because of that this solution can be reported as a semi-trivial one. Moreover, if one increase the damping coefficient in the pin joint of the second pendulum its motion would be not or barely observable. This solution is stable in almost the whole analysed range of parameter values except the narrow resonance tongue that occurs for $\omega =20\,[{\mathrm {rad/s}}]$. During experimental investigations four runs were performed, as we wanted to find the location of bifurcation lines predicted in the path-following analysis. In each run we slowly changed the value of $\omega$ until we reach the moment when the system jumps into another solution. The position of the branching bifurcation lines have been detected by path-following and confirmed using both experimental analysis and sample-based approach. The agreement between the results obtained using all three approaches is remarkably good. The second analysed solution is 1:2 oscillations which corresponds to the resonance tongue mentioned earlier (around $\omega =20\,[{\mathrm {rad/s}}]$). The results are shown in Fig. 11b. The path following analysis reveals that this solution loses its stability either in a saddle node bifurcation (for $A\le 5\,[10^{-3}{\mathrm {m}}]$) or in a symmetry braking bifurcation (for $A>5\,[10^{-3}{\mathrm {m}}]$) that is immediately followed by a cascade of period doubling bifurcations. The experimental analysis confirms that the position of the right-hand side border of the resonance tongue has been obtained with excellent precision. However, the detected range of stability differs from the results obtained via the numerical continuation. The difference is especially visible for $A=4\,[10^{-3}{\mathrm {m}}]$ (in horizontal direction) and for $\omega =16\,[{\mathrm {rad/s}}]$ in vertical direction. In these cases the sample-based method enables a better precision, especially when detecting the left-hand side border of stability. We see that the density of points decreases significantly before the bifurcation lines are reached. Thus, using the sample-based approach we can better predict the range in which it is possible to obtain 1:2 oscillations in real life. For the third analysed solution 1:3 oscillations the results from both methods of analysis are in good agreement with the experimental data [see panel (c)]. Similarly, for 1:6 oscillations [panel (e)] and 1:8 oscillations [panel (f)] we observe a concurrence of the results from all the applied methods. The difference between the experimental and numerical results is clearly distinguishable only in two cases. The experimental investigation revealed that the 1:6 oscillations can be achieved also below the line detected using the path-following method. Also, the position of a period doubling bifurcation which destroys the stability of 1:8 oscillations is different from what we observe experimentally. We think that the difference between the numerical results and the experiment mainly comes from the dissipation modelling approach which strongly simplifies the real phenomena [14, 49]. In panel (d) we show the results that correspond to 1:4 oscillations. For this solution, with the sample based approach can obtain the boundary of stability that better fits the experimental results then the bifurcation lines obtained via path-following method. It is especially visible for the left and the lower boundaries in the (A,  $\omega$) plane.

Fig. 11

Comparison between the ranges of stability obtained using the path-following method (colour lines), the sample-based approach (dots) and the experimental investigation (black lines). Each panel correspond to a different solution. Colour line type depicts the type of bifurcation. (Color figure online)

Having considered all oscillatory solutions we can now focus on the rotary ones. The results are presented in the last six panels (g–l) of Fig. 11. It is important to notice that we were unable to perform experimental analysis of last three rotary solutions, namely 2:3, 5:5, 6:6 rotations. We were only able to imitate 2:3 rotations but this solution is extremely susceptible to perturbations and the system jumps to another solution as soon as we try to change the amplitude or frequency of excitation, so it was impossible to reach the boundary of stability. In panel (g) we show the results obtained for 1:1 rotations of the second pendulum. This solution is stable in a noticeably wide range of excitation parameters and both numerical methods enable to predict the boundary of stability with good precision referring to the experimental result. Similar conclusions can be drawn from the analysis of the results obtained for 1:2 and 1:3 rotations that are shown in panels (h) and (i) respectively. Analysing the last three panels (j, k, l) of Fig. 11 we see that the location of stability boundaries predicted using the sample based procedure coincide with bifurcation lines calculated using the path-following method. To sum up, for all rotary solutions we see a good convergence between the results obtained using both numerical methods which reflects the gathered experimental data with good precision.

The results presented in Fig. 11 prove that for the considered system the path-following method and the sample-based approach offer similar accuracy. Also, when comparing the numerical results with the experimental data we observe good convergence. The advantage of the sample based analysis is that looking at the density of points we can also estimate the basin stability measure and probability density as described in the following sections. Such additional knowledge gives insight on the susceptibility to perturbations and one may expect the difficulties observed during experimental analysis. The important advantage of the sample-based approach is that during a large number of trials we are able to detect hidden attractors [27] or solutions with rather meager basins of attraction. In the investigated case we also found solutions that occurred only once for 172,500 trials, such as for example 2:5 oscillations or 3:15 rotations. Moreover, analysing Fig. 11, we see that with the sample-based approach we find the regions with the maximum density of points. This, in consequence enables to quantify the stability for different values of parameters using the basin stability measure or to prepare 2D probability density plots to find parameter values for which . To further investigate this topic for each solution we obtain maps indicating the changes of basin stability in the two-parameter space.

4.4 Basin Stability Maps

In the previous Section we show the results proving that the sample-based approach enables to predict the boundaries of stability with precision comparable to path-following method. Now, we show how we can utilize the results from the sample based method to obtain additional information about the system dynamics. In particular we will focus on the susceptibility to perturbations. The described algorithm is predisposed to such analysis because including random initial conditions we somehow investigate how the system reacts to sudden changes in working conditions. Basin stability measure is based on this concept and proved to be an efficient tool in a number of practical applications. Now we use data obtained from the aforementioned series of Bernoulli trials to analyse the changes of basin stability measure in the two parameter space. In Fig. 12 we demonstrate the results for all 12 considered solutions. It is important to notice that we use the grid that reflects the parameter ranges predefined in the calculation procedure and for each box we perform 500 trials. For all presented diagrams we hold the same colour scale for the basin stability that is given at the bottom of Fig. 12.

Fig. 12

Two parameters maps of the basin stability for 12 investigated solutions. The grid corresponds to the lattice used during the calculations. Below is the common basin stability scale used for all panels

Panel (a) refers to the 1:1 oscillations which has the largest range of stability (see Fig. 11a). The plot reveals that also in the large range of parameters this solution has basin stability greater than 0.5 so it has the dominant volume of the basin of attraction. In these ranges, with probability grater than 0.5 we expect that after random perturbation the system will end up in the basin of attraction of 1:1 oscillations. Thus, this solution has relatively low susceptibility to perturbations. Panels (b–f) correspond to the remaining oscillatory solutions. We see that for most of them, basin stability calculated in the assumed grid never exceeds 0.3. Still, for 1:2 and 1:4 oscillations we uncover regions with higher basin stability. Especially for 1:2 oscillations we observe increase of basin stability measure for $\omega \in [18.75,\,21.25]\,[{\mathrm {rad/s]}}$ and $A>0.004\,[{\mathrm {m}}]$, i.e., in the middle of the resonance tongue. For rotary solutions [panels (g–l)] we observe the similar structure of basin stability maps with maximum value of basin stability measure never exceeding. The only exception is the region around $\omega \in [25,\,35]\,[{\mathrm {rad/s}}]$ and $A>0.005\,[{\mathrm {m}}]$ where the probability of reaching 1 : 1 rotations is higher than 0.3.

Using the data obtained during the numerical procedure we can draw the 2D density plots reflecting continuous maps of basin stability (not using the lattice) by using interpolation. For that purpose we use the two-dimensional kernel density estimation in R software (R-project for statistical computing) [77]. With that functions we obtain plots presented in Fig. 13 that enables to detect where the given solution has the biggest relative volume of the basin of attraction. Thus, we are able to find the ranges in parameter space for which the solution is the most likely to appear and has low susceptibility to perturbations. The colour scale reflects the relative probability, so with such plots we cannot asses the value of basin stability measure but we can analyse the changes in the basins volume. Such plots are also convenient for estimating the boundary of stability.

Fig. 13

Two parameters probability density estimations for 12 investigated solutions. Below is the color scale for relative probability of reaching each solution. (Color figure online)

Analysing the results presented in Figs. 12 and 13 we can divide the considered range of parameter values into three regions:

• 1. The range where the semi-trivial solution has the dominant basin of attraction [see panels (a)].

• 2. The resonance tongue of 1:2 oscillations in which this solution has the biggest volume of the basin of attraction [see panels (b)].

• 3. The region where, the 1:1 rotations has the dominant basin of attraction and we observe the coexistence of many stable solutions [see panels (g)].

The above results prove that with the sample based procedure we are able to obtain additional knowledge about the systems dynamics that can be presented using basin stability maps (as show in Fig. 12) or probability density plots (as presented in Fig. 13).

4.5 Investigation with Parameters Mismatch

The important advantage of sample based methods is the ease to include parameters mismatch as described in [15]. It has huge practical importance, because we often cannot obtain the exact values of the system parameters [69]. The parameter identification procedure is especially difficult when the model contains parameters whose values cannot be measured directly such as, for example, a value of the viscous damping coefficient in a pin joint. Apart from that, when modelling the mechanical and structural objects, we often simplify complex phenomena using simple models. This can decrease the accuracy of simulations and cause the divergence between numerical and experimental results. In this section we show that the extended basin stability method can be applied without the knowledge of actual parameter values and still maintain the high accuracy of the yielded results.

Let us assume that we do not know precisely the values of some parameters of the system. In a classical approach, we have to set their values which may lead to wrong results. In the sample-based approach, instead of setting a value of the parameter, we can estimate the range to which this parameter belongs. Then, during a series of trials we draw the values of uncertain parameters. Before we apply that to our problem, we divide the parameters of our system (Eq. 12) into four specific groups basing on the ease of measurements:

• 1. Parameters that are easy to measure: $m_{1}$, $m_{2}$, $l_{1}$, $x_{1}$. This group contains the parameters that can be determined easily with good precision, namely masses and lengths of the physical objects. During calculations we assume that we determined values of these parameters precisely and do not draw them.

• 2. Parameters that can be estimated with good precision: $J_{1}$, $J_{2}$, $d_{1}$, $d_{2}$, k. The methods to measure these parameters values are not straight forward. In this group there are also parameters whose values are given by manufacturer with certain precision - as for example the stiffness of the spring. We assume that the error for the parameters from that group is $\pm 5\%$ and for each trial we draw the values of parameters from a certain range.

• 3. Parameters that are difficult to estimate: $c_{1}$, $c_{2}$. In this group we put parameters that require complex procedures or approach to infer their values and parameters that refers to phenomena that are difficult to model, such as energy dissipation. Values of parameters from this group are drawn from the range [80%, 120%] of the estimated value.

• 4. Parameters whose special influence we investigate: $A,\,\omega$. The aim of the study is to analyse the influence of these parameters on the stability of solutions. For these parameters we do not estimate the error. Instead, we draw values of these parameters from a “grid” as described in the Methods section.

Apart from the above, we want to maintain the value of the natural frequency of the second pendulum which can be easily measured using a simple stopwatch. For that purpose, we draw the inertia of the second pendulum and recalculate the position of its center of gravity to preserve the natural frequency.

With the above assumptions we repeat all the calculations. In Fig. 14 we present the comparison between the results obtained with fixed values of parameters and when drawing the parameter values. In the first two columns of Fig. 14 we show the results that refer to 1 : 2 oscillations and last two columns refers to 1 : 3 oscillations. In panels (a) and (e) we show the results from the sample based method with fixed parameters and in (b) and (f) the points obtained when drawing the parameter values. Similarly, we compare the maps of the basin stability for fixed parameters (c,g) and obtained with the assumed mismatch (d,h). Results that refer to the remaining 10 solutions are simmilar, hence we do not present them.

Fig. 14

Comparison between the results obtained from the model with and without the parameters mismatch. Panels (a, c, e, g) present the results from sample-based approach with fixed parameters while panels (b, d, f, h) with parameters mismatch (parameters are drawn from the assumed ranges)

The difference in the results from the extended basin stability analysis are barely visible despite the fact, that the positions of the bifurcation lines change when we modify the parameter values within the assumed ranges. This shows that the sample-based approach can be applied even without time consuming detailed measurements of the system’s parameters and still ensures sensible results. Instead of precisely measure the parameter values, we only have to asses the precision for each of the determined parameter.

4.6 Example of Practical Application

In this Section we apply the above described procedure to analyze the ranges of stability of different working regimes of the yoke-bell-clapper system described in Sect. 3.3. The system is multistable and there are two influencing parameters that can be changed to optimize working conditions while not affecting the generated sound, namely the amplitude of exciting torque $T_{max}$ and geometry of yoke given by parameter $l_{r}$ described in Fig. 7. Altering these two parameters we are able to change the response of the system significantly as described in [10]. Fig. 15a is a fragment of the plot presented and described in detail in [10]. It shows which type of proper working regime will be achieved assuming zero initial conditions ($\varphi _{1}=0.0$ [rad], $\varphi _{2}=0.0$ [rad], ${\dot{\varphi }}_{1}=0.0$ [rad/s], ${\dot{\varphi }}_{2}=0.0$ [rad/s]). Still, the results presented in Fig. 8 prove that due to multistability, for fixed parameter values we are able to obtain different working regimes by applying non zero initial conditions or using alternative starting procedure. This may be beneficial in practice as given bell can work differently depending on occasion. To enable such property we should know the precise boundaries of stability of solutions with respect to $T_{max}$ and $l_{r}$ as these parameters determine the needed power of linear motor propulsion and geometry of a yoke. This can be achieved using the sample based approach described above.

Fig. 15

Two parameter ringing schemes diagram showing the attractor reached starting from zero initial conditions. In the table we briefly characterize the possible solutions. For more details please see [10]

We consider the following ranges of parameters values: $T_{max}\in [100,\,300]$ [Nm] and $l_{r}\in [-\,0.3,\,0.2]$ [m] and run 400,000 simulations each time drawing values of $T_{max}$, $l_{r}$ and initial conditions from the ranges given in Eq. 11. We are especially interested in solutions that correspond to proper working regimes or have significantly large range of stability. Hence, we will only present ranges of stability for solutions given in the table on the right hand side of Fig. 15. The results are presented in Fig. 16. Each panel corresponds to different solution and presents the estimation of probability density of reaching it. Moreover, with white dashed lines we mark the regions in which the solution is reached from zero initial conditions.

Fig. 16

Two parameters probability density estimations for 6 investigated solutions. White dashed lines mark the region in which given solution is reached from zero initial conditions. Below is the color scale of the relative probability of reaching each solution

In panel (a) we show results for solution 1 (period 1 attractor with no impacts). We see that in the whole stability region the probability of reaching this attractor is similar and stability boundary overlaps with white dashed line which depicts the range of parameters for which solution 1 is reached from zero initial conditions. Such agreement is observed only for solution 1. Panel (b) refers to asymmetric falling clapper regime (solution 6 or 7) and we see that at the right hand side boundary of stability the probability of reaching this solution is gradually decreasing while it drops suddenly on the left boundary. There is a significant range of parameter values for which this solution coexists with symmetric falling clapper (solution 8) as shown in panel (c). In this multistable region solution 8 has dominant volume of basin of attraction. Panels (d) and (e) present the results obtained for solutions 9 and 12 respectively. In both cases the probability of reaching considered solution does not fluctuate strongly in the stability range. The overall probability of reaching a non periodic solution is shown in panel (f). The stability boundary more less overlaps with the white dashed lines which depict the range of parameters for which starting from zero initial conditions we do not reach proper working regime. However, between the white lines the probability of reaching non-periodic solution strongly varies. This means that in that range there are some stable attractors which was also detected in one parameter analysis (see Sect. 3.3) as shown in Fig. 8. We do not prepare additional plots for these solutions as they are not significant from practical point of view. It is important to notice, that even if there is only one stable attractor we can observe some variability of relative probability density. This is the effect of the sample based approach in which we do not ensure same density of trials in the analyzed parameters region. However, with sufficient number of trails we can neglect it. Summarizing, using the sample based approach we can prepare plots that precisely indicates the ranges of stability in two-parameters space and enables to determine parameter values that ensure biggest relative probability of reaching presumed solution.

5 Characterization of Phase Space Structure

Another important application of the sample based methods refers to the analysis of phase space organization which is largely unexplored especially for multi-degrees-of-freedom systems due to the computational challenge requested to build basins of attraction. Sample based analysis may help to overcome this problem. We propose to estimate the probability of reaching the attractors using a reasonable number of trials with random initial conditions. Then, we use the obtained results to investigate how this probability depends on particular generalized coordinate or a pair of coordinates. In the analysis we include all initial conditions, and reflect their influence on the final behaviour. The method allows to obtain information about the basins compactness and reveals particular features of the phase space topology. To analyse the trustworthiness of the proposed approach we compare the results with the classical computation of basins of attraction performed in the full range of initial conditions. Finally, we present example of practical application basing on the previously described hybrid dynamical model of the yoke-bell-clapper system.

5.1 Methodology and Exemplary Paradigmatic System

In this section we present the methodology basing on the analysis of the phase space structure of externally forced Duffing oscillator with attached pendulum. It is the model presented in Fig. 1a and described in Sect. 3.2. It is given by Eq. 2 but we change the parameter values to better fit the purpose. The parameters have the following values: $a=0.091$, $b=6.4$, $c=0.302$, $j=1,$, $d=3.37$, $h=0.0129$, $f=0.5$ and $\omega =1.1$, for which we observe two stable solutions. We start with explanation of the methodology and description of the presentation scheme for the obtained results. Then, we focus on the advantages of the sample based approach.

In the system we observe two stable solutions. The solution I is period-1 oscillation (it has the same period of the excitation) of mass M with pendulum remaining in the hanging down position. The second possible orbit (solution II) is period-2 solution (its period is double than that of the excitation) in which both mass M and pendulum performs oscillatory motion. At first, we consider the probability of reaching solution I from random initial conditions. We perform $2.5\times 10^{6}$ trials of direct numerical integration each time drawing the initial conditions from the following ranges $x\in \left[ -\,2,\,2\right]$, $\varphi \in \left[ -\pi ,\,\pi \right]$, ${\dot{x}}\in \left[ -\,2,\,2\right]$, ${\dot{\varphi }}\in \left[ -4,\,4\right]$. These ranges ensure that all stable solutions can be reached and refer to the practically accessible initial conditions that could be implied in the real world realization of the investigated system. The overall probability of reaching solution I is 54.3% which corresponds to basin stability measure of this attractor. Hence, the second solution has probability of reaching equal to 45.7%. Now, we want to investigate how this value change for different regions of the phase space.

5.1.1 One-Coordinate Histograms

Firstly, we consider how each particular coordinate influences the probability of reaching solution I. For this purpose we calculate histograms for each generalized coordinate separately. Each time we use 42 equal steps receiving on average 600,000 trials for each subset. In Fig. 17a–d we show how the probability of reaching solution I evolves with respect to coordinates x, ${\dot{x}}$, $\varphi$ and ${\dot{\varphi }}$ respectively. Each dot on the histograms corresponds to the series of trials in which all initial conditions are random but for one initial condition given on vertical axis we narrow down the range of drawing its value to $\frac{1}{42}$ of the whole accessible range. Hence, we see 42 discrete ranges which show the changes of probability as a function of one selected initial condition. Panel (a) shows how the probability of reaching solution I depends on the initial value of x. We see that there is no dominant trend and the value is scattered around the overall average probability. Hence, we expect that the initial value of x can affect the structure of basins of attraction, but not its overall volume. This is confirmed by the sample 3D projections of the full basins of attraction, obtained for $x_{0}=-\,2.0$, $x_{0}=0.0$ and $x_{0}=1.0$ presented in panels (a.1, a.2, a.3) respectively. Moreover, in our previous paper [8] we present supplementary material video1 which revels the evolution of 3D projection of the phase space for $x\in \left[ -\,2,\,2\right]$.

Fig. 17

Histograms showing how the probability of reaching solution I changes with respect to four generalized coordinates (a–d) supplemented by examples of 3D plots of basins of attraction

Panel (b) refers to the influence of initial condition ${\dot{x}}$ which is much less scattered.Thus, changes in initial value of ${\dot{x}}$ should have minor influence on the basins structure and compactness. It is also visible in the sample 3D plots (panels (b.1, b.2, b.3)) calculated for ${\dot{x}}_{0}=-\,2.0$, ${\dot{x}}_{0}=0.0$ and ${\dot{x}}_{0}=1.0$ respectively.

Panels (c) and (d) correspond to histograms calculated for $\varphi$ and ${\dot{\varphi }}$ respectively. In both plots we see similar shape of histograms. The probability is scattered on both ends of the considered ranges of initial conditions while in the middle there is clearly visible trend with the maximum around zero. Hence, we expect that around zero value the basins have large volume (maximum along the histogram) and more compact structure (clearly visible trend). Contrary, on both ends of the considered range we expect basins with smaller volume and more complex structure (lower probability and large dispersion in the histogram). These predictions are confirmed both on the sample 3D projections—panels (c.1, c.2, c.3, d.1, d.2, d.3). Animations showing full evolutions of the 3D basins of attraction can be found in the supplementary material to our recent paper [8]. The presented results show that one coordinate histograms may indicate the changes in the structure and volume of basins of attraction. We see that large dispersion along the histograms indicate fractal structure of basins while clearly visible trends refer to more compact shapes of basins. Apart from that, the proposed histogram plots can be used to detect the ranges of initial conditions for which we observe minimum or maximum volume of the basin of attraction.

5.1.2 Two-Coordinate Density Plots

In this section we consider 2D density plots showing how the probability of reaching solution I changes with respect to two particular coordinates. To obtain the density plot we perform large number of trials with random initial conditions. Then, we clusterize trials with respect to two initial conditions and for each group we calculate the probability of reaching solution I. By that, we obtain drawings that are somehow squeezed reflections of phase space that can be interpreted similarly as 1D histograms but brings more information. They are especially meaningful for mechanical systems because they are able to reflect the influence of the initial conditions of single degree of freedom (position and velocity). If we want to have the information how other pairs of initial conditions influence the density we can easily plot such diagrams. Moreover 2D plot is the limit of clear visualization method that enables convenient interpretation. The above reasons make the proposed density plots an efficient tool for the analysis of phase space structure.

In Fig. 18 we show 2D density plots obtained for the investigated system. In panels (a, b) we consider initial conditions that refer to separated single degree of freedom. In panel (a) we show how the probability is changing with varying x and ${\dot{x}}$. We see that for ${\dot{x}}\in \left( -1.6,\,1.4\right)$ the probability of reaching assumed solution is much larger than outside this range. The same conclusion can be drawn based on 1D diagram. The advantage of 2D plot is visible in the middle of the plot, where we clearly see that there is a narrow area of small probability (blue colour) in the high probability range. The second considered degree of freedom ($\varphi$, ${\dot{\varphi }}$) is shown in panel (b) of Fig. 18. The plot is significantly different from the first one. We observe a high probability in the center of plot and rapid decrease of probability outside this range. The highest probability is marked with dashed line ellipse.

Fig. 18

2D density plots presenting dependence of the overall probability of reaching solution I with respect to the initial state of Duffing oscillator (a) and pendulum (b). c, d Show basins of attraction calculated for points with minimum (c) and maximum (d) probability marked in a. The green and yellow color refer to basins of attraction of solutions I and II respectively. Dashed ellipse refers to the region in $\varphi$ and ${\dot{\varphi }}$ plane with high probability of reaching solution I. (Color figure online)

To present the advantage of 2D plots in panels (c) and (d) we show basins of attraction calculated for fixes initial conditions of the Duffing oscillator. The green and yellow colours refer to basins of attraction of solutions I and II respectively. Panel (c) corresponds to the point from panel (a) with minimum probability ($x=-\,0.24$, ${\dot{x}}=0.74$) and panel (d) refers to the point with maximum probability ($x=-0.18$, ${\dot{x}}=1.70$). Comparing panels (c) and (d) we see that indeed the amount of yellow colour that refers to solution II basins differs strongly. Moreover, on both plots we see unchanged range of high probability of reaching solution I marked with the dashed line ellipse [the same area as in panel (b)]. The above consideration shows that 2D density plots can be effectively utilized to investigate the structure of the phase space in multidimensional systems and provides additional knowledge over traditional presentation methods.

5.2 Practical Application

In this Section we one more time refer to the experimentally validated model of the yoke-bell-clapper system described in Sect. 3.3. We analyse the structure of the phase space for the following set of parameter values: $T_{max}=230$ [Nm], $l_{r}=-\,0.075$ [m]. Analyzing Figs. 8 and 16 we see that two stable attractors coexist for that case. Both of them are falling clapper hence the collisions between the bell and the clapper occur when they perform an anti-phase motion. The first attractor corresponds to asymmetric falling clapper with one impact per period of motion (solution 6 or 7) and the second one to symmetric falling clapper with two impacts per period—one on each side of the bell (solution 8). Assuming the ranges of applicable initial conditions given by Eq. 11 we analyze the structure of the phase space.

Results are presented in Fig. 19 where the first three panels (a, b, c) refer to the relative probability of reaching solution 6 or 7 and panels (d, e, f) placed in the lower row reflect the results for solution 8. In the first column we present the influence of initial angular position and velocity of the bell while in the second column of the clapper. We see that to obtain the symmetric solution with two impacts per period (solution 8) we have to imply some initial deflection of the bell and the clapper.

Fig. 19

2D density plots presenting dependence of the overall probability of reaching coexisting stable solutions with respect to the initial state of the bell (a, d), the clapper (b, e) and initial deflections of the bell and the clapper (c, f). The color scale is presented at the bottom of the figure. (Color figure online)

It is also much easier to obtain precise initial deflection than angular velocity. Hence, for practical application, in the last column we plot how the relative probability depends on the initial deflections of the bell and clapper. The white triangles reflect the geometrical boundaries of accessible initial states of the system (as aforementioned the initial angular potions of bell and clapper must fulfil the relation $\left| \varphi _{1_{0}}-\varphi _{2_{0}}\right| <\alpha$, see Eq. 11). Panels (c, f) are of practical importance as they indicate that it is impossible to reach symmetric solution without implying some specific initial state of the system or sophisticated starting procedure.

6 Conclusions

Recent rapid increase in computational power and ensuing development of parallel computing create immense opportunities for novel sample based methods of dynamical analysis. At first glance, these methods seem complex and sophisticated as they need powerful numerical apparatus. Still, they enable to reproduce the inherent uncertainty of perturbations and have numerous advantages which make them appropriate especially for analysis of multistable systems.

The first is the fact that we are able to detect all possible solutions also hidden and rare attractors. This feature is extremely important when analyzing systems with unknown number of possible stable solutions. With sample based methods we are able to detect all solutions with basin stability greater than some threshold that depends on the number of trials. We can create basin stability maps or two-dimensional probability density plots to show ranges of stability and find parameter values that ensure the highest possible basin stability measure. The presented results prove that sample based algorithm ensures precision similar to classical methods (direct numerical integration, path-following) and the obtained results reflect the experimental data.

Secondly, we are able to investigate the ranges of stability in multiple parameters space including parameters mismatch and variation of parameter values. We can take into account the fact that values of parameters are measured or estimated with some finite precision and also that they can slightly change during normal operation. We can extend the analysis by adding model imperfections or different types of noise. The obtained results enable to assess the robustness of solutions and estimate the risk of unwanted behavior. Moreover, with sample based methods we can concurrently investigate dynamics in multiple parameters space.

The last revealed application of the sample based approach is analysis of the phase space structure of mulit-DOF dynamical systems. The proposed method enables to investigate the influence of particular initial condition. The presented results show that the method enables to obtain additional knowledge of the basin compactness and reveal regions in the phase space that have some specific features. Crucial part of the approach is proposed presentation scheme that enables to overcome some limitations of the currently know methods. Probability histograms are useful to analyze single initial condition and detect ranges with maximum or minimum probability of reaching the solution of interest. Two dimensional density plots correspond to squeezed reflections of phase space and reveal the influence of given degree-of-freedom or a pair of initial conditions. These plots are obtained assuming random initial conditions, hence they uncover the overall influence of considered the initial condition or conditions.

The above advantages prove that sample based methods are efficient tool that can be effectively utilized to investigate the dynamics of wide range of dynamical systems and provide additional knowledge over traditional methods.