1 Introduction

The International Maritime Organization (IMO) requires that all new ships meet minimum energy efficiency levels according to the Energy Efficiency Design Index (EEDI). This requirement can be satisfied by reducing emissions, a measure that also decreases fuel costs. To reach this goal, optimizing a ship’s hull for least resistance became a relevant design issue because hull shape significantly affects ship performance. Successful optimization involves geometric variation of the hull form. Combined with computational fluid dynamics (CFD) methods, we applied a computer-aided design (CAD) method to parametrically model and subsequently optimize the hull shape of three generic containerships.

Parametric modeling techniques in CAD can be subdivided into three phases, namely, wireframe modeling, surface modeling, and solid modeling. Of these, a fully parametric modeling method portrays the entire hull, whereas a partially parametric model describes only the changed part of an existing hull. Tin and Tun (2016), for example, employed a partially parametric model to optimize the bulbous bow of a containership. The fully parametric modeling method is the preferred approach to improve the efficiency at the early stages of ship design. Nowacki (1977) used the fully parametric design method to optimize hull curves by means of cubic B-splines with vertices obtained from form parameters. Kracht (1978) presented a set of form coefficients to characterize a bulbous bow and concluded that the volumetric parameter has the largest influence on resistance. Employing hull parametric modeling, Kracht and Jacobsen (1992) defined certain parameters to control the hull form of a new model series, the so-called D Series, originating from a twin-screw round bilged ship. Harries and Abt (1998) selected 13 parameters representing positional, integral, and differential shape requirements to generate a flexible geometry that adopted these shape requirements. Harries (1998) developed a special technique to simplify the generation of the parametric hull form via surface curves using form parameters that control the hull from. This parametric approach was fully based on uniform B-spline curves, and form parameters defined the hull surfaces via a variation formula. Brizzolara et al. (2015) compared two parametric approaches, namely, the free-form deformation (FFD) approach and the full parametric approach (FPA). They found out that the FPA approach is better able to provide feasible and realistic hull forms, both in terms of stability of the optimization procedure and design viability of the attained optimum shape. Therefore, we applied also the FPA approach to generate parametric models.

Automatic optimization procedures are computationally demanding. A surrogate-based optimization can be used to reduce the computational burden. Queipo et al. (2005) presented an overview of surrogate-based optimizations. They compared several approaches in design space sampling, surrogate model construction, model selection and validation, sensitivity analysis, and surrogate-based optimization. The surrogate acceleration technique has been widely used in ship design and optimization. Scholcz et al. (2015) used surrogates to obtain approximate Pareto fonts for a chemical tanker. They found that the ship design process can be accelerated, leading to more efficient ships. Rotteveel et al. (2016) studied the effect of numerous hull forms and conditional variations. They applied surrogate models for different water depths for the final design trade-offs. Scholcz and Veldhuis (2017) reduced the computer time from two weeks to only one day by using the surrogate-based global optimization (SBGO) technique instead of a multi-objective genetic algorithm (MOGA). They demonstrated that the SBGO technique is a promising approach to mitigate the computational burden for multi-dimensional design spaces or multi-level optimization problems that arise naturally in naval ship designs.

Our aim was to apply an automatic optimization process on three different sized of containerships, namely, the Duisburg Test Case (DTC), the Kriso containership (KCS), and the S-175 containership. For the DTC, El Moctar et al. (2012) provided experimental results based on model tests for benchmarking. Previous research of El Moctar et al. (2017) numerically investigated wave added resistance for this ship and for a cruise ship using the two Reynolds-averaged Navier-Stokes (RANS) solvers, OpenFOAM and COMET. They applied an implicit solver to compute nonlinear six degrees-of-freedom ship motions and obtained comparable results that agreed fairly well with model test measurements. Riesner and El Moctar (2018) developed a nonlinear time-domain Rankine source method to calculate the wave-induced added resistance of the DTC and a large tanker at constant forward speed in regular head waves. Riesner et al. (2018) computed speed loss, engine output, and fuel consumption for this DTC, for the KVLCC2 tanker, and for a cruise ship.

For the KCS, research involved model testing at the Korean Research Institute of Ships and Ocean Engineering (Van 1997; Van 1998a, b) and at the Ship Research Institute of Japan (Kume 2000). Larsson et al. (2003) selected the KCS for one of their self-propulsion test cases to validate predicted mean velocities, surface pressures, wave profiles, and resistances for this ship under stern flow conditions with and without an operating propeller. Kim et al. (2001) provided a benchmark database using CFD techniques to validate ship hydrodynamic predictions, including global forces, wave patterns, and local mean velocity components around the KCS measured in a towing tank. Zhang (2010), computing the flow around the KCS on three computational grids, verified and validated resistance predictions and wave profiles based on ITTC (2002a) recommended procedures. Gaggero et al. (2015) used an OpenFOAM RANS solver to predict calm water resistance and propeller open water characteristics for the KCS. Chen et al. (2019) performed RANS simulations to calculate the resistance of a model of the KCS under similar conditions.

For the S-175, Fujii (1975) conducted numerous experimental investigations and numerical simulations to predict the wave added resistance and the corresponding motions in regular waves. Fonseca and Guedes Soares (2004), after carrying out experiments on a model of the S-175 at constant speed in regular head waves, demonstrated that the nonlinear behavior of the vertical responses is similar at Froude numbers between 0.15 and 0.25. Papanikolaou and Liu (2010) implemented a three-dimensional frequency domain panel code in their method to predict the wave added resistance of the S-175 in waves, and they showed that their method is reliable and robust for routine predictions of the wave added resistance of a ship in waves. Somayajula et al. (2014) developed a three-dimensional panel code based on Green functions to determine the S-175’s wave-induced motions and wave added resistance using the near field pressure integration technique. Kim et al. (2017) applied a two-dimensional and a three-dimensional flow scheme and an unsteady Reynolds-averaged Navier-Stokes (URANS) approach to predict motions and wave added resistance of the S-175 in regular head and oblique waves.

Applying the fully parametric modeling technique of CAESES, we generated a parametric hull of the DTC, i.e., a hull of a containership with a bulbous bow. We used this process also for the hull of the smaller but similar KCS containership by changing only the parameters. For the smallest S-175 containership, which is a hull without a bulbous bow, we generated another parametric hull, and for this hull and its optimal hull, we carried out numerical simulations. For the two containerships DTC and KCS, we analyzed total resistance at various speeds under calm water conditions and compared results with experimental data. The wave added resistance of DTC at the Froude number of 0.139 and KCS at the Froude number of 0.26 in head waves was predicted and compared with experimental results. For S-175, we also predicted the added resistance at the Froude number of 0.250 in regular waves and compared the results with corresponding experimental data. The potential flow solver GL Rankine performed all our numerical simulations. This solver is a nonlinear free surface Rankine panel method. Heinrich et al. (2014) employed a new Rankine panel method and an extended RANS solver to predict wave added resistance in head waves at different Froude numbers of a Wigley hull, a large tanker, and a modern containership. They concluded that the potential flow method GL Rankine was appreciably faster than the RANS solver for the prediction of wave added resistance of ships in waves. Meanwhile, RANS-based simulations provided validation data for potential codes. With this validated potential code, as in our previous work, where we optimized the hull of a wind offshore supply vessel (Feng et al. 2020a), we combined GL Rankine with CAESES using two different genetic algorithms. Here in this study, to reduce the computational effort, we relied on the SBGO optimization algorithm implemented in the open source software DAKOTA (Adams et al. 2009). Similar process was developed in our previous work for DTC (Feng et al. 2020b). The parametric hull created for DTC is used here to check whether it is suitable to KCS, which has a similar ship hull as DTC. We compared results of our optimization process with experimental data from former researchers’ work and analyzed the influence of optimal hulls on the resistances of these three containerships. The influence of the optimization process on different sizes of containerships is discussed and analyzed.

2 The Subject Containerships

We considered three differently sized containerships, here identified as DTC, KCS, and S-175. The DTC is a modern 14000TEU post-Panamax container carrier, the so-called Duisburg Test Case (DTC). Its hull was developed at the Institute of Ship Technology, Ocean Engineering and Transport Systems (ISMT). The KCS is the well-known 3600TEU KRISO containership test case. It was designed by the Maritime and Ocean Engineering Research Institute (MOERI) to provide data to examine flow physics and to validate CFD computations for a modern container ship with a bulbous bow and a bulbous stern. The S-175 is one of the benchmark hull forms used by researchers to study its seakeeping capability. Figure 1 shows the original hull forms of these vessels, and Table 1 lists their principal particulars. An IGES model of the DTC was available from ISMT (2012), and model data and test conditions of the KCS were documented by MOERI (2008).

Figure 1
figure 1

Original hull forms of the DTC (top), the KCS (center), and the S-175 (bottom)

Full size image
Table 1 Principal hull particulars of the DTC, the KCS, and the S175
Full size table

3 Parametric Modeling

The new hull form, i.e., a three-dimensional parametric model was created from a set of parameters that relate hull dimensions and selected design constraints. By changing one of these parameters, the other parameters that depend on these parameters were automatically updated. The parts to be optimized were cut out or removed and finally replaced by a parametric geometry. We optimized the entire hull body of the subject containerships. Therefore, we replaced the imported IGES model files with a parametric model. We relied on fully parametric modeling to create a parametric model of the ships’ hulls, which were defined by specific design requirements satisfied by generating or changing specific descriptors.

Obtaining a parametric model required three steps. First, basic curves had to be confirmed; second, curve engines had to be defined; third, meta surfaces had to be generated. Most curves of the parametric model were obtained using poly-curves with F-splines that allowed the user to control the entrance and the run angle of each curve and the area and centroid of some segments of the curve. To achieve this goal, some parameters were created for the entrance and run angles, and other parameters that represented an area coefficient for the segments were manipulated when needed.

The first step to generate an F-spline was to obtain input form parameters, such as start and end points, entrance locations, and run angles. We used a parameter named “fullness” to change different areas of curves. Figure 2 presents an example of an F-spline with three different area constraints. The fullness of curves C1, C2, and C3 was 1.0, 0.5, and 1.5, respectively. We obtained the needed curves by changing the chosen design variables, such as entrance angle, run angle, and fullness. We divided the parametric design of the hull form into four phases, namely, specification of main particulars, obtaining the basic parametric design curves, determining the parametric design section curves, and generating the hull form.

Figure 2
figure 2

Fairness-optimized parametric curves with different area constraints

Full size image

3.1 Specifying the Hull’s Main Particulars

To satisfy specific requirements, we specified principal dimensions and coefficients, such as Lpp, B, T, and CB. The overall dimensions defined the frame of the ship hulls.

3.2 Parametric Design of Basic Curves

The model for the hull surface of each ship was primarily constructed of basic curves, which were determined by the parameters. Starting from the stem, these curves comprised bulbous bow curves, longitude curves, and diagonal curves.

  1. 1)

    A bulbous bow, if designed appropriately, reduces the ship’s resistance, and, therefore, its shape is relevant for hull design. Curves to create the bulbous bow were grouped as follows: top elevation curves for the upper profile (TopElevation), keel elevation curves for the lower profile (KeelElevation), beam elevation curves for the height at maximum width (BeamElevation), and beam curves for the maximum width of the beam curves (MaxBeam). Longitudinal positions (Xpos) were specified for each of these curves, and fullness curves (FullnessCurves) and tangent curves (TangentCurves) defined entrance and run angles of each curve.

    Both DTC and KCS have bulbous bows, while the S-175 does not. For the KCS, we used the profile curves of the DTC as we only had to change the parameters to fit the size of the KCS’s hull. For the S-175, instead of creating curves for its bulbous bow, we used only one single curve to control the stem of its hull. The fullness of the stem curve determined the shape of the stem. Figure 3 presents the difference between profile curves of the bulbous bow for the DTC and the KCS as well as of the stem profile for the S-175. This figure shows perspective views to better identify these curves for each hull. All subsequent figures refer to these three hull forms, created by following the same procedure.

  2. 2)

    For the DTC and the KCS, the longitude curves that modeled the hull frame comprised deck curves (Deck), over deck curves (Overdeck), the design waterline (DWL), flat of side curves (FOS), flat of bottom curves (FOB), center plane curves (CPC), and transom curves (Transom). For the S-175, the longitude curves comprise only DECK, FOS, DWL, FOB, and CPC curves. Figure 4 shows longitude curves of each hull.

  3. 3)

    For the DTC and the KCS, three diagonal curves (diagonal 1, diagonal 2, and diagonal 3) controlled the shape of their stern. For the S-175, only one single stern curve was created to control the shape of its stern; see Figure 5.

Figure 3
figure 3

Profile curves of the bulbous bow of the DTC (left) and the KCS (center), and the stem profile of the S-175 (right)

Full size image
Figure 4
figure 4

Longitude curves of the hull for the DTC, the KCS, and the S-175

Full size image
Figure 5
figure 5

Profile curves of the ships’ aft body for the DTC, the KCS, and the S-175

Full size image

3.3 Parametric Design of Ship Sections

To create meta surfaces with adequate accuracy for the parametric models, we defined additional cross sections extending from stem to stern as shown in Figure 6. As seen, only the DTC has a midbody, while the KCS and the S-175 do not. We created the parametric hull for the DTC, which has a midbody length of 24.4m. Therefore, when applying the parametric model to the KCS, the midbody had to be deleted. However, deleting the midbody directly would have destroyed their connections, but connections were necessary to regenerate a new parametric hull. As creating new connections was time-consuming, we assumed the length of the midbody to be relatively small. Then the midbody was slim enough to be considered as a line. Here, for the KCS we assumed a length of 0.1 m for its midbody. The parametric hull of the DTC was not suitable for the S-175, because its shape was too different. For the S-175, we created a new parametric hull without a midbody and, instead, we constructed a midship line.

Figure 6
figure 6

Ship section curves along the longitudinal direction for the DTC (top), the KCS (center), and the S-175 (bottom)

Full size image

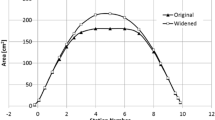
Figure 6 shows 13 section lines along the longitudinal direction of the DTC’s hull and, due to its missing the midbody, one section line less on the KCS’s hull. For the S-175, only eight sections sufficed to define the entire hull because diagonal curves were not required for its stern and its midbody. All longitudinal positions were individually specified. Table 2 lists the positions of these sections for the DTC, the KCS, and the S-175 as well as relevant details. The entry “None” in this table means that sections did not exist for the associated ship hull.

Table 2 Definition of section positions of the DTC, the KCS, and the S-175
Full size table

3.4 Generation of Hull Forms

A generated parametric hull consisted of so-called meta surfaces as seen in Figure 7. A meta surface is a parametric sweep surface subject to several user controls. Hence, it is a highly flexible surface, especially convenient for efficient shape optimization by means of a simulation tool. The following three steps were necessary to generate a meta surface:

  1. 1)

    Curve definition: the custom curve definition was based on feature definitions that specified, for example, the type of curve, their start and end points, and their entrance and run angles.

  2. 2)

    Curve engine setup: the curve engine connected the functional curves defined in step 1.

  3. 3)

    Meta surface generation: meta surfaces were created within a specified interval using the curve engine of step 2.

Figure 7
figure 7

Parametric hulls for the DTC, the KCS, and the S-175

Full size image

Figure 8 shows comparative body plans and side profiles of the parent hull and the parametric hull for the DTC, KCS, and S-175. Blue lines mark bodylines of the original hulls; red lines, bodylines of the parametric hulls. As seen, for DTC and KCS, compared to the original bodylines, the parametric bodylines differ only slightly. This demonstrated that it was possible to apply the parametric hull of DTC also to the similar hull of the KCS by changing the corresponding design variables. In the same way, this parametric hull can be applied to other containerships with a similar hull, which helped to reduce computational costs. For the S-175, these differences were comparatively greater than for the other two hulls. We started with offset values of the S-175 to specify the input information of the other hulls, which led to somewhat irregular bodylines of the original S-175 hull. The changed hull form and its optimization were then based on the parametric hull. However, the resulting slight difference was a measure for reliable results.

Figure 8
figure 8

Comparative body plans and side profiles of the parent hull (blue) and the parametric hull (red) for the DTC, KCS, and S-175

Full size image

4 Numerical Approach

4.1 Linear Reponses in Waves Using Rankine Sources

The GL Rankine method we applied is a frequency domain method based on Rankine sources. Söding et al. (2012) developed this code to calculate frequency dependent hydrodynamic response coefficients and diffraction forces. This method accounts for the interaction between the nonlinear stationary flow in calm water (including steady ship waves and dynamic trim and sinkage) and the periodic flow in waves. In potential theory, the fluid is assumed to be ideal, i.e., incompressible and inviscid, and the flow is assumed irrotational. If the flow velocity is an irrotational vector field, a velocity potential exits. The total potential ϕt(ωe) in waves is assumed to be a superposition of the steady potential −ux + ϕ0 and the periodic potential of complex amplitude \(\hat{\phi^1}\), which oscillates with encounter frequency ωe:

$${\phi}^t\left(\boldsymbol{x},\boldsymbol{t}\right)= ux+{\phi}^0\left(\underline{\boldsymbol{x}}\right)+\text{Re}\left(\hat{\phi^1}{\mathrm{e}}^{\mathrm{i{\omega}}_et}\right)$$
(1)

where \(\underline{\boldsymbol{x}}\) designates the same location as \(\underline{\boldsymbol{x}}\) expressed in a coordinate system fixed to the ship’s hull. It is assumed that ϕ1depends linearly on the wave amplitude.

The dynamic boundary condition is expressed as follows:

$${ \begin{array}{c}\nabla \phi^0 -\boldsymbol{U}\left[\nabla \hat{\phi^1}+\boldsymbol{a}\times \nabla {\phi}^0-\left({\nabla}^2{\phi}^0\right)\boldsymbol{v}\right]\\ {}+\mathrm{i}{\upomega}_e\left(\hat{\phi^1}-\boldsymbol{v}\nabla {\phi}^0\right)+g\left(\hat{\zeta^1}-\boldsymbol{v}\nabla {\upzeta}^0\right)=0\end{array}}$$
(2)

where U = [u, 0, 0]T denotes the ship velocity vector of the steady inflow, \(\hat{\boldsymbol{a}}\) the amplitude of the ship rotation vector, \(\hat{\boldsymbol{v}}\) the amplitude of the total motion of a point on the ship, i the imaginary unit number, and ζ0 = ζ0(x, y) the free surface elevation. The superscript 0 is used for the steady solution. The kinematic boundary condition reads as follows:

$${ \begin{array}{c}\mathrm{i}{\omega}_e\left(\hat{\zeta^1}-\hat{\boldsymbol{v}}\nabla {\upzeta}^0\right)+\nabla {\upzeta}^0\nabla \hat{\phi^1}+\left(\nabla {\phi}^0-\boldsymbol{U}\right)\nabla \hat{\zeta^1}\\ {}+\frac{\partial }{\partial z}\hat{\phi^1}+\hat{\boldsymbol{a}}{\left[-\frac{\partial {\phi}^0}{\partial y},\frac{\partial {\phi}^0}{\partial x},u\frac{\partial {\upzeta}^0}{\partial y}\right]}^T+\hat{A}=0\end{array}}$$
(3)

where \(\hat{A}\) includes all second order derivatives and is written as follows:

$$\hat{A}=\frac{-\hat{\boldsymbol{v}}{\boldsymbol{n}}^0}{{\left|{\boldsymbol{n}}^0\right|}^2}{\boldsymbol{n}}^0\left[\left({\nabla}^2{\phi}^0\right){\boldsymbol{n}}^0+\left({\nabla}^2\zeta^0\right)\left({\nabla}{\phi}^0-\boldsymbol{U}\right)\right]$$
(4)

where n0 is the normal vector of the stationary free surface:

$${\boldsymbol{n}}^0={\left[\frac{{\partial \zeta}^0}{\partial x},\frac{{\partial \zeta}^0}{\partial y},-1\right]}^{\mathrm{T}}$$
(5)

Relying on the approach of Hachmann (1991), terms involving second derivatives of the steady potential are transformed from the body boundary condition to the kinematic boundary condition on the free surface. Based on experience, this approach ensures more accurate results, particularly at large Froude numbers. Söding et al. (2012) described additional details about this frequency domain approach. The special feature of Hachmann’s strip method is that the steady flow filed follows not only the average forward motion of the ship, but also participates in the periodic flow motion. This, together with the interaction between the steady potential ϕ0 and the periodic first-order potential \({\phi}_1\left(\boldsymbol{x},t\right)=\mathbf{\text{Re}}\hat{\Big({\phi}^{1}}{\mathrm{e}}^{{\mathrm{i}\omega}_et}\Big)\), yields more accurate predictions at higher forward speeds.

In Eq. (1), the difference between vectors x in inertial coordinates and \(\underline{\boldsymbol{x}}\) in body-fixed coordinates is described by the following second-order equation:

$$\boldsymbol{x}=\underline{\boldsymbol{x}}+{\boldsymbol{v}}_{\mathbf{1}}+{\boldsymbol{v}}_{\mathbf{2}}$$
(6)

where \({\boldsymbol v}_{\mathbf2}=\boldsymbol a\times\left(\boldsymbol a\times\underline{\boldsymbol x}-{\underline{\boldsymbol x}}_g\right)/2\) represents first-order terms, and \({\boldsymbol v}_{\mathbf1}=\boldsymbol u+\boldsymbol a\times\left(\underline{\boldsymbol x}-{\underline{\boldsymbol x}}_g\right)\) represents second-order terms, respectively. Here, u denotes the displacement of the ship’s center of gravity and a the rotation of the hull.

The second-order force is separated into two main contributions, namely, the pressure force FA acting on the hull up to the average waterline (expressed in hull-bound coordinates) and the force FB caused by the variation of hull submergence. Force FB is the sum of three contributions:

(7)

where indices 0, 1, and 2 designate the order of pressure \({\underline{p}}\) in hull-fixed coordinates and of the area vectors f of the panels in inertial coordinates. Area vectors f are normal vectors on hull panels, pointing into the hull, with magnitudes equal to panel areas. They are defined as follows:

$${\boldsymbol f}_0=\underline{\boldsymbol f},\;{\boldsymbol f}_1=\boldsymbol a\times\boldsymbol f,\;{\boldsymbol f}_{\mathbf2}=\boldsymbol a\times\left(\boldsymbol a\times\boldsymbol f\right)/2$$
(8)

Pressure of order 0, 1, and 2 are defined as follows:

$${\hat{\underline{p}}}_0/\rho =- gz$$
(9)
$${p}_1/\rho =\text{Re}\left({\hat{p}}_1{\mathrm{e}}^{-\mathrm{i}{\omega}_et}\right)/\rho$$
(10)

with

$${ \begin{array}{c}{\underline{\hat{p}}}_1/\rho =-\left(\nabla {\phi}^0-\boldsymbol{U}\right)\left(\nabla \hat{\phi}+\boldsymbol{a}\times \nabla {\phi}^0\right)\\ {}-\mathrm{i}{\omega}_e\left(\hat{\phi}-{\hat{v}}_1\nabla {\phi}^{\mathbf{0}}\right)-g{\hat{v}}_{1z}\end{array}}$$
(11)

and

$${ \begin{array}{l}{\underline{\hat{p}}}_2/\rho =-{\dot{\boldsymbol{v}}}_2\nabla {\phi}^0+{\dot{\boldsymbol{v}}}_1\left(\nabla \nabla {\phi}^0\right){\boldsymbol{v}}_1+\left(\boldsymbol{a}\times {\boldsymbol{v}}_1\right)\nabla {\phi}^0\\ {}-\nabla {\dot{\phi}}^1{\boldsymbol{v}}_1-{g\boldsymbol{v}}_{2z}-{\left(\nabla {\phi}^1-\nabla {\phi}^0\times \boldsymbol{a}\right)}^2/2\\ {}\begin{array}{l}-\left(\nabla {\phi}^0-\boldsymbol{U}\right)\cdot \Big[{\boldsymbol{v}}_1\nabla \nabla {\phi}^0\times \boldsymbol{a}+\left({\boldsymbol{v}}_1\times \boldsymbol{a}\right)\nabla \nabla {\phi}^0\\ {}+{\boldsymbol{v}}_1\nabla \nabla {\phi}^1-{\boldsymbol{v}}_1\left(\nabla \nabla \nabla {\phi}^0\right){\boldsymbol{v}}_1\Big]\end{array}\end{array}}$$
(12)

respectively. Symbol ∇∇ in the expression ∇ ∇ ϕ0 denotes an outer product, producing a matrix when applied to a scalar. Symbol ∇ ∇ ∇ in the expression ∇ ∇  ∇ ϕ0 also denotes an outer product, producing a tensor of third-order when applied to a scalar.

The three terms in parentheses A, B, and C in Eq. (7) comprise two harmonically oscillating factors contributing to the second-order force and moments, denoted as \(a=\text{Re}\left(\hat{a}{\mathrm{e}}^{\mathrm{i{\omega}}_et}\right)\) and \(b=\text{Re}\left(\hat{a}{\mathrm{e}}^{\mathrm{i{\omega}}_et}\right)\). The product of factors a and b are written as follows:

$${ \begin{array}{l} ab=\text{Re}\left(\hat{a}{\mathrm{e}}^{\mathrm{i{\omega}}_et}\right)\text{Re}\left(\hat{b}{\mathrm{e}}^{\mathrm{i{\omega}}_et}\right)\\ {}=\text{Re}\left[\hat{a}{\mathrm{e}}^{\mathrm{i{\omega}}_et} \text {Re}\left(\hat{b}{\mathrm{e}}^{\mathrm{i{\omega}}_et}\right)\right]\\ {}\begin{array}{l}=\text{Re}\left[\hat{a}{\mathrm{e}}^{\mathrm{i{\omega}}_et}\ \frac{1}{2}\text{Re}\right(\hat{b}{\mathrm{e}}^{\mathrm{i{\omega}}_et}+\left({\hat{b}}^{\ast }{\mathrm{e}}^{-\mathrm{i{\omega}}_et}\right)\Big]\\ {}=\frac{1}{2}\text{Re}\left(\hat{a}\hat{b}{\mathrm{e}}^{2\mathrm{i{\omega}}_et}+\hat{a}{\hat{b}}^{\ast}\right)\end{array}\end{array}}$$
(13)

where the upper index ∗ designates the complex conjugate. The first term oscillates harmonically at frequency 2ωe; its time average is zero. Therefore, the time average of ab is as follows:

$$\overline{ab}=\frac{1}{2}\text{Re}\left(\hat{\mathrm{a}}{\hat{b}}^{\ast}\right)$$
(14)

This formula is used to evaluate the time-average of a product of two first-order quantities. The time averages of terms A and B in Eq. (7) are thus evaluated as follows:

$$\overline{A}=\frac{1}{2}\text{Re}\left(\hat{\boldsymbol{\upalpha}}\times {{\hat{p}}^{\ast}}_1\underset{\_}{\boldsymbol{f}}\right),\overline{B}=\text{Re}\left[\hat{\boldsymbol{\upalpha}}\times \left({\hat{\boldsymbol{\upalpha}}}^{\ast}\times {p}_0\underset{\_}{\boldsymbol{f}}\right)\right]$$
(15)

To determine the time average of \({\underline{p}}_2\) at hull-fixed points in the term C in Eq. (7), terms containing third-order space derivatives of steady potential ϕ0 are neglected, which yields the following result:

$${ \begin{array}{l}\overline{C}=\frac{\rho {\boldsymbol{f}}_0}{2}\text{Re}\left\{\mathrm{i}{\omega}_e\left(\hat{\boldsymbol{\upalpha}}\times {\hat{\boldsymbol{v}}}_1^{\ast}\right)\nabla {\phi}^0-\mathrm{i{\omega}}_e\nabla \hat{\phi}{\hat{\boldsymbol{v}}}_1^{\ast}\right\}\\ {}+\frac{1}{2}{\left[0,0,-g\right]}^{\mathrm{T}}\Big[\hat{\boldsymbol{\alpha}}\times \left({\hat{\boldsymbol{\alpha}}}^{\ast}\times \underline{\boldsymbol{x}}\Big)\right]\\ {}\begin{array}{l}-\frac{1}{2}{\left|\nabla \hat{\phi}-\nabla {\phi}^0\times \hat{\boldsymbol{\alpha}}\right|}^2\\ {}-\left(\nabla {\phi}^0-\boldsymbol{U}\right)\Big[{\hat{\boldsymbol{v}}}_{\mathbf{1}}\nabla \nabla {\hat{\phi}}^0\times {\hat{\boldsymbol{\alpha}}}^{\ast}\\ {}-\left({\hat{\boldsymbol{v}}}_{\mathbf{1}}\times {\hat{\boldsymbol{\upalpha}}}^{\ast}\right)\nabla \nabla {\phi}^0+{\boldsymbol{v}}_1\nabla \nabla {\hat{\phi}}^{\ast}\left]\right\}\end{array}\end{array}}$$
(16)

The time-averaged value of the remaining force contribution FB caused by the varying hull submergence is as follows:

$$\overline{{\boldsymbol{F}}_B}=\sum\limits_{\text{WL}\ \text{panels}}\frac{{\left|{\hat{p}}_w\right|}^2}{4\rho g}\ \frac{{\Delta} _s\left(\underline{\boldsymbol{f}}\times {{\Delta} }_s\right)}{{\left(\underline{\boldsymbol{f}}\times {{\Delta} }_s\right)}_3}$$
(17)

where \({\hat{p}}_w\) is the pressure oscillation amplitude on the time-averaged waterline and \({\hat{p}}_w/\left(\rho g\right)\) is the linearized vertical relative motion between the water surface and hull, including swell-up. Waterline (WL) panels are panels on the hull surface with two of their three corners located on the waterline, ∆S is the vector between these corners, and index 3 designates the vertical component. Second-order moments are calculated in a similar way.

4.2 Calm Water Resistances

Hughes (1954) proposed that total resistance RT can be described as the sum of wave resistance RW and frictional resistance RF, formulated as follows:

$${R}_T={R}_W+\left(1+k\right){R}_F$$
(18)

where k is the form factor, which is generally calculated based on experimental data. It can be also estimated using for instance RANSE-CFD code with double-body flow at the model scale. The double body flow method dictated that the flow around the underwater body is symmetrical without free surface. In this situation, the form factor is expressed as 1 + k = CV/CF, CV is the viscous pressure coefficient, which was obtained from the simulation results from Starccm+, and CF could be obtained by Eq. (20). Detail calculation process can be found in the research of Dogrul et al. (2020). With this method, we obtain the form factors for DTC, KCS, and S-175, which are 0.094, 0.155, and 0.129, respectively.

Wave resistance Rw was calculated directly using code GL Rankine. To determine the total resistance, the tangential contribution due to viscosity, i.e., the frictional resistance RF, was also needed. It was estimated as follows:

$${R}_w=0.5\rho {V}^2{SC}_F$$
(19)

for a water density of ρ = 998.8 kg/m3 and for ship speed, V, where S is the wetted area of the hull. The normalized resistance coefficient CF, according to the ITTC (1957), was expressed as follows:

$${C}_F=\frac{0.075}{{\left({\log}_{10}\left(\mathit{{Re}}\right)-2.0\right)}^2}$$
(20)

where Re = VL/v is Reynolds number, L is ship length between perpendiculars, and v = 1.09 × 10−6 m2/s is kinematic viscosity of water.

4.3 Wave Added Resistance

A ship sailing in the sea encounters waves from different directions. The total resistance in waves RTw consists of calm water resistance Rcw and wave added resistance Raw. It was expressed as follows:

$${R}_{Tw}={R}_{cw}+{R}_{aw}$$
(21)

Angle μ represented the wave heading angle as shown in Figure 9. In head waves, μ = 180°; in beam waves from port, μ varies between 60° and 120°. Here we only computed the added resistance in regular waves and the associated the heave and pitch motions in head waves.

Figure 9
figure 9

Definition of incident wave directions

Full size image

Using the GL Rankine code, we obtained the Froude-Krylov force, the radiation and diffraction forces, the waterline force, and the time-averaged drift force. The time-averaged drift force represents the wave added resistance Raw. An associated normalized wave drift force, here known as the wave added resistance coefficient Caw, was expressed as follows:

$${C}_{aw}=\frac{R_{aw}}{\rho g{\xi}^2{B}^2/L}$$
(22)

where ρ, g, and ξ are density, gravitational acceleration, and wave amplitude, respectively, and Raw is the average value of added resistance obtained directly from numerical simulations. For comparison with experimental results, we presented the mean added resistance of this ship in waves by this added resistance coefficient.

The ship motions were normalized as follows:

$$\ddot{\theta}=\frac{\theta_a\ L}{2\pi \xi}$$
(23)
$$\ddot{z}=\frac{z_a}{\xi }$$
(24)

where θa and Za are, respectively, pitch and heave amplitude. Symbol ¨ identifies normalized values.

4.4 Numerical Performance

In the simulation solver GL Rankine, we used unstructured grids with triangular panels on the submerged body surface and block-structured grids with quadrilateral panels on the free surface. Due to the symmetric structure of ships, only half of the ships’ bodies and free surfaces were discretized. The same grid was used on a body, both for the steady and seakeeping problems. Typically, about 2000 panels per half body were employed. According to Riesner et al. (2019), a medium size grid of about 2000 panels was sufficiently fine to obtain reliable resistance predictions. Therefore, we could just set up the panel number in the reliable range; the grid study process could be omitted. Here we performed our GL Rankine computations (at model scale) for the DTC, the KCS, and the S-175 on grids comprising 1723, 2178, and 2187 panels, respectively, as shown in Figure 10.

Figure 10
figure 10

Comparison of panels of the model scaled ship DTC, KCS, and S-175 for GL Rankine computations

Full size image

5 Multi-Objective Optimization Problem

We formulated our general optimization problem as follows:

$$\text{Minimize}:f\left(\boldsymbol{x}\right),\boldsymbol{x}\in {\mathfrak{R}}^n$$
(25)
$$\text{Subject to}:\kern0.5em { \begin{array}{c}{\boldsymbol{x}}_l\mathbf{\le}\boldsymbol{x}\mathbf{\le}{\boldsymbol{x}}_u\\ {}{\boldsymbol{g}}_l\mathbf{\le}\boldsymbol{g}\left(\boldsymbol{x}\right)\mathbf{\le}{\boldsymbol{g}}_u,\boldsymbol{h}\left(\boldsymbol{x}\right)={\boldsymbol{h}}_t\\ {}{\boldsymbol{a}}_l\le {\boldsymbol{A}}_l\left(\boldsymbol{x}\right)\le {\boldsymbol{a}}_u,{\boldsymbol{A}}_e\left(\boldsymbol{x}\right)={\boldsymbol{a}}_t\end{array}}$$
(26)

In this formulation, f(x)is the objective function, while x = [x1, x2, ⋯xn]T is an n-dimensional vector of real-valued design variables. Vectors xl and xu specify the lower and upper bounds of design variables, respectively. These bounds ensured that design variables changed within a reasonable range. The optimization goal was to minimize the objective function f(x), while satisfying the constraints. These constraints were categorized as linear or nonlinear and as an inequality or an equality. The linear inequality constraints created a linear system Al(x), where Al is the coefficient matrix for the linear system and al and au are their lower and upper bounds, respectively. The linear equality constraints created a linear system Ae(x), where Ae is the coefficient matrix for the linear system and vectors at specify the target values. Vectors g(x) designate the nonlinear inequality constraints with lower and upper bounds gl and gu, respectively. The nonlinear equality constraints h(x) had target values specified by ht. The constraints partitioned the parameter space into feasible and infeasible regions. A feasible design point had to satisfy all constraints.

5.1 Objective Functions

The objective functions to be minimized were the wave resistance RW and the frictional resistance RF, both of which were described above.

5.2 Constraints

In the process of optimization, the selection of constraints was difficult. The entire hull form optimization was formulated to minimize total resistance under design conditions while satisfying the geometric constraints. The new hull form was subject to the following constraints:

  • Change of total displacement was limited to one percent of the original displacement.

  • Change of the longitudinal center of buoyancy was limited to one percent of the original longitudinal center of buoyancy.

  • Change of the metacentric radius was limited to one percent of the original metacentric radius.

To obtain a reliable and flexible hull, technological constraints had to be considered as well. These constraints provided the upper and lower bounds of the design variables.

5.3 Sensitivity Analysis

A sensitivity analysis identified design parameters that had the greatest influence on response quantities. We employed framework CAESES and its optimization package DAKOTA to analyze the sensitivity of design variables and to identify those variables that significantly affected hull resistance. DAKOTA was useful for multi-objective optimizations, parameter predictions, uncertainty analyses, and sensitivity analyses.

Here, we exemplarily analyzed the sensitivity of the DTC’s hull. Our executable file for this sensitivity analysis considered 100 samples. We analyzed the sensitivity of design variables for three parts of the hull, namely, the bulbous bow (14 parameters), the forebody (10 parameters), and the aftbody (13 parameters). Based on these results, we selected seven design parameters for the bulbous bow, five design parameters for the forebody, and six parameters for the aftbody. Due to the similarity of hull shapes of the DTC and the KCS, the selected design variables for the KCS were the same as those for the DTC.

Table 3 lists these design variables and their definitions. To meet ship stability requirements, the parametric model was only allowed to be changed within in a predefined range.

Table 3 Design variables, their definitions, and their lower and upper limits for the DTC and the KCS
Full size table

Table 3 includes also the lower and upper limits of the design variables for the DTC and the KCS. Unlike the DTC and the KCS, the S-175 does not have a bulbous bow. Therefore, the selected design variables for the S-175 differed from those for the DTC and the KCS. Table 4 lists the design values for the S-175, the limits of the selected design variables, and the associated lower and upper limits.

Table 4 Design variables, their definitions, and their lower and upper limits for the S-175
Full size table

Taking the DTC as an example, Figures 11, 12 and 13 plot the influence of each design variable on ship resistance components RW and RF for the bulbous bow, the forebody, and the aftbody, respectively. It is worthy to mention that because we used potential solver to predict the resistance, that is, the pressure viscous resistance was not considered in this process. The changes of resistance on the aftbody, see Figure 13, were caused by the deformation of the stern. The individual graphs in these figures include straight (least squares) red lines drawn through the resulting values of RW and RF to demonstrate the influence of the changing parameter values.

Figure 11
figure 11

Sensitivity analysis of the seven design variables for the bulbous bow of the DTC (Feng et al. 2020b)

Full size image
Figure 12
figure 12

Sensitivity analysis of the five design variables for the forebody of the DTC (Feng et al. 2020b)

Full size image
Figure 13
figure 13

Sensitivity analysis of the six design variables for the aftbody of the DTC (Feng et al. 2020b)

Full size image

6 Optimization Algorithm

In general, there is no unique optimum to design a multi-objective optimization problem. However, there is a set of points that represents the best compromise between different objectives, the so-called Pareto optimal values. Genetic algorithms are frequently used to perform multi-objective optimizations. We applied the surrogate-based global optimization (SBGO) method for multi-objective optimizations in CAESES with DAKOTA.

Often, extensive calculations are necessary to evaluate the generated data. To reduce the computational effort of the optimization process, surrogate-based acceleration techniques can be used. Figure 14 presents the framework of the optimization process of Forrester and Keane (2009). This global method was originally designed for a multi-objective genetic algorithm (MOGA). In this method, the MOGA is conducted on an iteratively built-up surrogate model. For the initial model, data from the sensitivity analysis can be recycled as well. Since MOGA needs thousands of points to produce optimal solutions, surrogates can help by reducing the necessary model evaluations.

Figure 14
figure 14

Framework of a surrogate-based optimization process of Forrester and Keane (2009)

Full size image

7 Results and Discussion

Due to their similar hull forms, simulation results and flow patterns were similar for the DTC and the KCS. For the DTC, we analyzed the influence of design variables on RW and RF and then listed the changes of resistance after the ship hull was optimized. After that, we calculated the dimensionless added resistance coefficient Caw of ship in head waves at Fr = 0.139 for DTC and at Fr = 0.260 for KCS. For the KCS, we compared wave profiles of the optimized hull with experimental data, and, instead of analyzing the resistance, we compared the simulated resistance coefficients with experimental results. These coefficients expressed the resistance values normalized against dynamic pressure times nominal wetted area. For the S-175, we simulated wave-induced the ship motions at Fr = 0.250 and compared these with experimental data.

7.1 The DTC

7.1.1 Calm Water Resistance

We demonstrated the use of a multi-objective optimization procedure to optimize the hull of the DTC for least resistance. We relied on fully parametric modeling to generate the hull in CAESES. The wave resistance and frictional resistance components were the objective functions. Figures 11, 12 and 13 graphically illustrate the influence of the selected design variables on the objective functions, i.e., on the two resistance components RW and RF.

In Figure 11 we see that, for the bulbous bow, the influence of design variables Bulblength, yBeamStart, and xTop on RW and RF oppose each other. For the other four design variables, the influence of design parameters on RW and RF is the same. Specifically, the trend of variable Bulblength shows that the longer bulb decreased wave resistance and increased frictional resistance.

In Figure 12 we see that, for the forebody, the influence of design variables fullnessDWL and EntranceTanDWL on RW and RF oppose each other. For the other three design variables, the influence of design parameters on RW and RF is the same. Specifically, the trends of the variable fullness of the DWL indicate that the fuller forebody decreased wave resistance and increased frictional resistance.

In Figure 13 we see that, for the aftbody, the influence of design variables fullnessTransom, fullnessFOBaft, fullnessDiag1, and fullnessDiag3 on RW and RF oppose each other. For the other two design variables, the influence of design parameters on RW and RF is the same. Specifically, the trends of variable fullnessTransom indicate that the fuller transom increased wave resistance and decreased frictional resistance.

Figure 15 compares the parametric hull and the optimal hull at design speed (Fr = 0.218) of the DTC, and Figure 16 compares the DTC’s parametric and optimal forebody and the aftbody. From these figures, we can see that the optimized hull has a longer and sharper bulbous bow than the parametric hull, and its keel region is slightly wider at the aftbody than the parametric hull.

Figure 15
figure 15

Comparison of the parametric hull and the optimal hull for the DTC at design speed

Full size image
Figure 16
figure 16

Comparison of the parametric hull and optimal hull of the forebody and the aftbody for the DTC at design speed

Full size image

After developing the parametric hull, we employed the validated potential flow code GL Rankine to compute wave resistance for the original hull, the parametric hull, and the optimal hull. For the six Froude numbers considered, Table 5 lists the resulting resistances for the parametric hull (Par) and the optimal hull (Opt) and the associated percentage reduction (Diff). At these Froude numbers, ranging from 0.174 and 0.218, optimizing the parametric hull reduced wave resistance by at least 44.47% and by at most 67.15%. At medium speeds, the decrease of wave resistance for the optimized hull was less than at low or high speeds.

Table 5 Comparative calm water resistances of the parametric hull (Par) and the optimal hull (Opt) and their differences (Diff) for the DTC
Full size table

Apart from the resulting wave and frictional resistances, Table 5 also lists the total resistance we obtained for the parametric hull and the optimal hull and their percentage difference. For the six Froude numbers considered, the optimization decreased total resistance for the parametric hull by at least 2.02% and by at most 4.15%. These changes of total resistance show the same trend as the wave resistance. Thus, the successful reduction of wave resistance after optimization led to a decrease of total resistance for the optimized hull.

To compare these results, Figure 17 plots total resistance for the original hull, the parametric hull, and the optimal hull together with experimental data. Computed and experimental results differed by small amounts. The window inserted in this figure shows an enlarged view of the difference between the three hulls and the experimental data. For the six Froude numbers considered, Table 5 lists the resulting total resistance for the parametric hull and the optimal hull and the associated percentage reduction. As seen, at these Froude numbers, ranging from 0.174 and 0.218, the optimization affected frictional resistance only marginally.

Figure 17
figure 17

Comparison of total resistance for the original hull, the parametric hull, and the optimal hull of the DTC with experimental data

Full size image
Figure 18
figure 18

Wave added resistance coefficients and total resistance for the DTC in head waves at Fr = 0.139

Full size image
Figure 19
figure 19

Heave and pitch responses for the DTC in head waves at Fr = 0.139

Full size image

We stated total resistance for the DTC via its resistance coefficient, expressed as the total resistance normalized by the dynamic pressure and the nominal wetted area according to the ITTC (2002b) formula as follows:

$${C}_T=\frac{R_T}{0.5{\rho SV}^2}$$
(27)

Table 6 lists the resistance coefficient for the DTC at six different Froude numbers obtained from experiments (Exp) (El Moctar et al., 2012), from GL Rankine simulations for the parametric hull (GLR), and from GL Rankine simulations for the optimal hull. The percentage differences (Diff) of these coefficients for the parametric and optimal hull are also listed in Table 6. From this table we can see that, at Froude numbers ranging between 0.174 and 0.218, the total resistance coefficient of the optimal hull was reduced by at least 1.81% and by the most 3.83%. Comparing with low and middle speeds, the reduction of total resistance coefficient increased at higher speeds.

Table 6 Comparative resistance coefficients obtained from experiments (Exp), from GL Rankine simulations of the parametric hull (GLR), from GL Rankine simulations of the optimal hull (Opt), and their differences (Diff) for the DTC
Full size table

Figure 20 plots the comparison results more intuitively. From this figure we can see that, the calculated results with GL Rankine code were bigger than the experimental data. But it shows the same tendency as the experimental results.

Figure 20
figure 20

Comparative total resistance coefficients for the DTC

Full size image

7.1.2 Resistance in Regular Waves

Simulations were performed for DTC advancing at Fr = 0.139 in regular head waves of different wavelengths with λ/Lpp ratios ranging between 0.45 and 2.5. The wave frequency ranged between 2.2 and 5.6 rad/s. Figure 18 plots wave added resistance coefficients and total resistances, respectively, against wave length to ship length ratio λ/Lpp for the DTC in regular head waves at Fr = 0.139, and Figure 19 plots the associated heave and pitch responses against wave length to ship length ratio λ/Lpp, also under these condition. Solid lines mark results for the parametric hull of the DTC obtained from code GL Rankine; dashed lines, the corresponding results for the optimal hull. Red squares represent experimental data provided by the Technical University Berlin (TUB). The DTC model was tested at the former Berlin Model Basin VWS at a scale of 1:89.11. Blue triangles represent experimental model tests of MARINTEK at a scale of 1:63.65 under deep water conditions.

As seen, added resistance coefficients based on GL Rankine computations are similar to added resistance coefficients based on experimental measurements. For the optimal hull, wave added resistance coefficients are slightly reduced at λ/Lppof about 1.0. The trends of total resistance of the original hull and optimal hull of the DTC are similar to the trends of wave added resistance coefficient. Numerical results of heave and pitch responses are almost identical when λ/Lpp < 0.5. At λ/Lpp of about 1.0, numerically predicted heave response exceeds experimental measurements, while numerically predicted pitch response is only slightly higher than the experimental measurements. After the optimization process, heave and pitch responses in head waves changed only marginally when λ/Lpp < 1.0.

During all model tests, the DTC model was equipped with segmented bilge keels and a single rudder. However, our numerical simulations of the DTC were performed for the model without a rudder. As the rudder’s contribution to overall resistance consisted mainly of friction, we evaluated its frictional resistance Rfr as follows:

$${R}_{fr}={R}_F\frac{S_r}{S}$$
(28)

where Sr is the wetted surface of rudder. For the DTC, the rudder is totally underwater. Thus, its wetted surface represents its area. According to classification society rules (DNVGL 2015), the frictional resistance caused by the rudder is less than 0.4% of total resistance. Therefore, the influence of the rudder was small enough to be neglected.

7.2 The KCS

7.2.1 Calm Water Resistance

Due to similar hull shape of the DTC and the KCS, we chose the same design variables and objective functions for the KCS, and their design variables had the same influence on wave resistance and frictional resistance as for the DTC. Hence, we omitted the process of selecting design variables for the KCS and described the optimal results directly. Figure 21 compares the parametric (original) hull and the optimal hull for the KCS at design speed (Fr = 0.260), and Figure 22 compares the associated parametric and optimal forebody and the aftbody. These figures show that the optimal hull is longer and has a sharper bulbous bow than the original hull, while the aftbody is only slightly altered after optimization. Therefore, here too we concluded that a longer and sharper bulbous bow lowered the resistance of the KCS’s hull.

Figure 21
figure 21

Comparison of the parametric hull and the optimal hull for the KCS at design speed

Full size image
Figure 22
figure 22

Comparison of the parametric hull and the optimal hull of the forebody and the aftbody for the KCS at design speed

Full size image

We considered six Froude numbers ranging from 0.108 to 0.282. Table 7 lists the comparative resistances for the parametric hull (Par) and the optimal hull (Opt) of the KCS. The optimization reduced wave resistance of the parametric hull at least by 38.22% and at most by 98.29%. At low speeds, the decrease of wave resistance for the optimized hull was more than at medium or high speeds. From the frictional resistance results, we see that the frictional resistance only decreased at least by 0.09% and at most by 1.21%. These results were similar to those we obtained for the DTC, i.e., the optimization affected frictional resistance only marginally. For total resistance, the optimization decreased for the parametric hull at least by 2.65% and at most by 10.78%. These changes of total resistance also show the same trend as the wave resistance.

Table 7 Comparative calm water resistances of the parametric hull (Par) and the optimal hull (Opt) and their differences (Diff) for the KCS
Full size table

To validate our simulated results, we compared the GL Rankine computed wave profiles obtained for the parametric and the optimal hull with experimentally measured wave profiles. Figure 23 plots these profiles as normalized wave elevations, z/Lpp, versus normalized horizontal distance from amidships, x/Lpp, where solid lines identify computed results for the parametric hull; dotted lines, computed results for the optimal hull; and black dots, experimental results for the model tested hull. This figure depicts also two so-called wave cuts, located at y/Lpp = 0.0741 and at y/Lpp = 0.1509. These wave cuts are wave profiles as they appear on a vertical plane parallel the hull’s center plane located some distance from its centerline. Although the wave profile along the hull was generally well predicted by the GL Rankine method, the first wave peak and the second wave trough are somewhat under predicted. Nevertheless, in general, the predicted results compared favorably to the experimental results. For the optimal hull, wave peaks are lower and wave troughs are higher, and the first wave peak is slightly over predicted. These results demonstrated that the predicted wave field compared favorably to the measurements. Especially at the bow, the agreement is excellent in terms of both wave elevation and shape of the diverging wave groups.

Figure 23
figure 23

Comparison of wave profiles on the hull, on the wave cut at y/Lpp = 0.0741, and on the wave cut at y/Lpp = 0.1509

Full size image

We validated our predictions not only of total resistance, but also of the ship’s sinkage and its trim against experimental data. Table 8 lists the resistance coefficient for the KCS at six different Froude numbers obtained from experiments (Exp), from GL Rankine simulations for the parametric hull (GLR), and from GL Rankine simulations for the optimal hull. Also listed are the percentage differences (Diff) of these coefficients for the parametric and the optimal hull. We see that, at Froude numbers ranging between 0.108 and 0.282, the total resistance coefficient of the optimal hull was reduced by at least 1.87% and by at most 10.77%. At the ship’s design speed (Fr = 0.260), the decrease of total resistance for the optimized hull was more than at lower speeds. Generally, at higher speeds, the reduction of total resistance increased.

Table 8 Comparative resistance coefficients obtained from experiments (Exp), from GL Rankine simulations of the parametric hull (GLR), from GL Rankine simulations of the optimal hull (Opt), and their differences (Diff) for the KCS
Full size table

Table 9 and 10 list, respectively, comparative values of sinkage and trim. As seen, over the range of ship speeds considered, optimizing the hull led to a relatively large reduction of trim and only slight decrease of sinkage. Specifically, optimizing the hull caused trim to decrease by at least by 4.71% and by at most 17.09% and sinkage to decrease by at least only 4.30% and by at most only 6.38%. At lower and higher speeds, the reduction of trim was larger than at medium speeds.

Table 9 Comparative values of sinkage obtained from experiments (Exp), from GL Rankine simulations of the parametric hull (GLR), from GL Rankine simulations of the optimal hull (Opt), and their differences (Diff) for the KCS
Full size table
Table 10 Comparative values of trim obtained from experiments (Exp), from GL Rankine simulations of the parametric hull (GLR), from GL Rankine simulations of the optimal hull (Opt), and their differences (Diff) for the KCS
Full size table

Figure 24 summarizes these results graphically, showing plots of total resistance coefficients and values of sinkage and trim obtained from experiments (Exp), from GL Rankine simulations of the parametric hull (GLR), and from GL Rankine simulations of the optimal hull (Opt).

Figure 24
figure 24

Comparative total resistance coefficients and values of sinkage and trim for the KCS

Full size image

7.2.2 Resistance in Regular Waves

Simulations were performed for KCS advancing at Fr = 0.260 in regular head waves of different wavelengths with λ/Lpp ratios ranging between 0.3 and 2.1. Wave frequencies ranged between 2.0 and 5.4 rad/s. Figure 25 presents comparative wave added resistance coefficients and total resistances of the KCS in regular head waves of different encounter frequencies at Fr = 0.260. Figure 26 presents the heave and pitch responses for the KCS under the same condition. Similar to the results of DTC, solid lines mark results for the parametric hull of the KCS using GL Rankine code; dashed lines, results of the optimal hull. Red squares and blue triangles, respectively, represent experimental data of Sadat-Hosseini et al. (2015) for the ship model with length 2.10 m and for the ship model with length 6.07 m. The orange dot represents the experimental data of Simonsen et al. (2013) for the ship model with length 4.37 m. As seen, the general trend of numerical results and experimental data of wave added resistance coefficient are consistent, but the numerical wave added resistance coefficients are slightly lower than the experimental ones when λ/Lpp< 1.0. The wave added resistance coefficients for the optimal hull are lower than those for the original hull when λ/Lpp> 1.0. Especially when λ/Lpp in the range 1.2 and 1.4, this reduction is noticeable. Similar observations apply by comparing the total resistance of the original hull and optimal hull. The numerical results of heave and pitch responses are slightly higher than the experimental results when 1.0 < λ/Lpp< 1.8. After the optimization process, heave and pitch responses in head waves changed only marginally.

Figure 25
figure 25

Wave added resistance coefficients and total resistance for the KCS in head waves at Fr = 0.260

Full size image
Figure 26
figure 26

Heave and pitch responses for the KCS in head waves at Fr = 0.260

Full size image

7.3 The S-175

7.3.1 Calm Water Resistance

The hull shape of the S-175 differed from the hull shapes of the DTC and the KCS. Figure 27 compares the original hull and the optimal hull for the S-175 at the Froude number of Fr = 0.250, and Figure 28 compares the associated original and optimal stem and stern configurations. These figures show that the optimal hull has a longer stem and a thinner stern, which was also the case for the DTC and the KCS.

Figure 27
figure 27

Comparison of the original hull and the optimal hull for the S-175 at Fr = 0.250

Full size image
Figure 28
figure 28

Comparison of stem and stern of the original and the optimal hull for the S-175 at Fr = 0.250

Full size image

Table 11 lists comparative resistances for the parametric hull (Par) and the optimal hull (Opt) for the S-175 at the Froude number of Fr = 0.250 under calm water conditions. Symbol Diff represents for the difference values of resistance between parametric hull and optimal hull. Wave resistance, RW, was reduced by 45.14% after the ship was optimized. Similar to the results of the DTC and the KCS, the frictional resistance, RF, increased by 2.2%. However, the total resistance, RT, decreased by 8.71% after the optimization process.

Table 11 Comparative calm water resistances of the parametric hull (Par) and the optimal hull (Opt) and their differences (Diff) for the S-175 at Fr = 0.250
Full size table

7.3.2 Resistance in Regular Waves

Figure 29 shows the numerical results of wave added resistance coefficient and total resistance for different incident wave amplitudes for the ship S-175 at Fr = 0.250 in regular head waves. Figure 30 presents the heave and pitch responses under the same conditions. Solid lines identify computed results for the parametric hull; dashed lines, computed results for the optimal hull; red squares, experimental results of Fujii (1975); blue dots, experimental results of Nakamura and Naito (1977); green triangles, experimental results of Fonseca and Guedes Soares (2004). The left figure indicates that the results from the GL Rankine method agree reasonable well with the experimental results. The results of optimal hull for S-175 show a remarkable reduction on both wave added resistance coefficient and total resistance when λ/Lpp > 1.0. The left graph of Figure 30 shows that the results from the GL Rankine method overestimated the heave motions compared with experimental data when λ/Lpp is in the range between 1.2 and 1.6. Nevertheless, the computed values followed the same trend as the experimental data. The right graph of Figure 30 shows that the numerical results of pitch motions are close to the experimental data of pitch motions. The difference of heave and pitch motions between the original and the optimal hull for the S-175 was minimal. Therefore, the changing design variables for the ship hull hardly influenced heave and pitch motions in head waves.

Figure 29
figure 29

Wave added resistance coefficients and total resistance for the S-175 in head waves at Fr = 0.250

Full size image
Figure 30
figure 30

Heave and pitch responses for the S-175 in head waves at Fr = 0.250

Full size image

8 Conclusions

Applying fully parametric modeling method, we created parametric hulls for three different sizes of containerships. Due to high similarity, the parametric hull for DTC can be applied on KCS after changing the corresponding parameters. As the KCS did not have a parallel midbody, a comparatively small value was assigned to its midbody to control its length. This reduced computational costs for generating a new parametric hull. Similarly, it can be also used to other containerships that are similar to DTC (i.e., a bulbous bow included). After the parametric hull was generated, with wave resistance and frictional resistance as the objective functions, the open source software DAKOTA was applied to develop the optimization procedure and to obtain the optimal hull shapes. To simulate the involved resistance, we employed the potential code GL Rankine to compute calm water resistance. The influence of ship sizes on the optimization process is compared and analyzed. Based on the optimization results, we predicted the wave added resistance and ship motions in head waves for the optimal hulls at certain Froude numbers (DTC, Fr = 0.139; KCS, Fr = 0.260; S-175, Fr = 0.250). The influence of the optimal hull on wave added resistance and ship motions were analyzed. The numerical results were compared with corresponding experimental data. All experimental measurements available for comparison with numerical results were obtained from model tests. Therefore, to avert scaling errors, all numerical investigations were conducted at model scale. The scale ratios for DTC, KCS, and S-175 were 1/59.407, 1/31.599, and 1/40, respectively.

The optimizations of ship hulls under calm water conditions led to several conclusions. First, for the two larger containerships (with a bulbous bow), a longer sharper bulbous bow and a wider keel at the aftbody reduced wave resistance and, for the smaller containership (without a bulbous bow), a longer stem and a thinner stern reduced wave resistance. Second, at lower speeds, wave resistance for the optimized hulls was decreased by a larger amount than at medium and higher speeds. Third, at the considered range of Froude numbers, the optimization affected frictional resistance only marginally. Forth, the decrease of total resistance in calm water showed the same trend as the decrease of wave resistance. Fifth, for the studied containerships in this paper, the size of containerships did not show obvious and regular influence on the optimization results.

The GL Rankine code was employed to perform linear seakeeping analyses for three ships in regular head waves. Heave and pitch responses and wave added resistances agreed reasonably well with experimental measurements. Numerical results of optimal hulls of the three different size containerships demonstrated that the optimal hulls reduced wave added resistance and total resistance, especially for the small containership. However, the optimization process only slightly affected ship motions in head waves.