Abstract
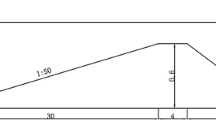
Green-Naghdi (G-N) theory is a fully nonlinear theory for water waves. Some researchers call it a fully nonlinear Boussinesq model. Different degrees of complexity of G-N theory are distinguished by “levels” where the higher the level, the more complicated and presumably more accurate the theory is. In the research presented here a comparison was made between two different levels of G-N theory, specifically level II and level III G-N restricted theories. A linear analytical solution for level III G-N restricted theory was given. Waves on a planar beach and shoaling waves were both simulated with these two G-N theories. It was shown for the first time that level III G-N restricted theory can also be used to predict fluid velocity in shallow water. A level III G-N restricted theory is recommended instead of a level II G-N restricted theory when simulating fully nonlinear shallow water waves.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Demirbilek Z, Webster WC (1992a). Application of the Green-Naghdi theory of fluid sheets to shallow-water waves, Report 1, Model formulation. US Army Wat. Exp. Sta., Coastal Engng. Res. Cntr., Vicksburg, Technical Report No. CERC-92-11.
Demirbilek Z, Webster WC (1992b). User’s manual and examples for GNWAVE. US Army Wat. Exp. Sta., Coastal Engng. Res. Cntr., Vicksburg, Technical Report No. CERC-92-13.
Green AE, Laws N, Naghdi PM (1974). On the theory of water waves. Proc R Soc Lond A, 338, 43–55.
Luth HR, Klopman G, Kitou N (1994). Kinematics of waves breaking partially on an offshore bar: LVD measurements for waves without a net onshore current. Delft Hydraulics, Delft, The Netherlands, Technical Report No. H1573.
Madsen PA, Bingham HB, Liu H (2002). A new Boussinesq method for fully nonlinear waves from shallow to deep water. Journal of Fluid Mechanics, 462, 1–30.
Madsen PA, Bingham HB, Schafer HA (2003). Boussinesq-type formulations for fully nonlinear and extremely dispersive water waves: derivation and analysis. Proc R Soc Lond A, 459, 1075–1104.
Rienecker MM, Fenton JD (1981). A Fourier approximation method for water waves. Journal of Fluid Mechanics, 104, 119–137.
Wang Yanying (2008). Discussion on the parameters of design waves. Journal of Marine Science and Application, 7(3), 162–167.
Webster WC, Kim DY (1990). The dispersion of large-amplitude gravity waves in deep water. Proceeding of 18th Symposium on Naval Hydrodynamics, National Academy Press, Michigan, 397–415.
Zhao Binbin, Duan Wenyang (2009). Research on the Green-Naghdi theory for fully nonlinear deep water waves. Journal of Harbin Engineering University, 30(8), 860–866. (in Chinese)
Author information
Authors and Affiliations
Corresponding author
Additional information
Foundation item: Supported by the National Natural Science Foundation of China under Grant No. 50779008 and the 111 Project (B07019).
Bin-bin Zhao was born in 1984. He is presently a PhD candidate for fluid mechanics at Harbin Engineering University. His current research interests include Green-Naghdi theory and nonlinear wave-body interactions based on BEM.
Wen-yang Duan was born in 1967. He is a professor and a PhD supervisor at Harbin Engineering University. His current research interests include nonlinear wave-body interactions, SPH method and Boussinesq model.
Rights and permissions
About this article
Cite this article
Zhao, Bb., Duan, Wy. Fully nonlinear shallow water waves simulation using Green-Naghdi theory. J. Marine. Sci. Appl. 9, 1–7 (2010). https://doi.org/10.1007/s11804-010-9031-y
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11804-010-9031-y