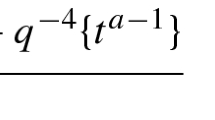Towards Generalized Riesz Systems Theory

Abstract

Pseudo-Hermitian Hamiltonians have recently become a field of wide investigation. Originally, the generalized Riesz systems (GRS) have been introduced as an auxiliary tool in this theory. In contrast, the current paper, GRSs are analysed in terms of basis theory. The relationship between semi-regular sequences and GRSs is provided. Various characterizations of GRSs are discussed.

1 Introduction

Theory of non self-adjoint operators attracts a steady interests in various fields of mathematics and physics, see, e.g., [7] and the reference therein. This interest grew considerably due to the recent progress in theoretical physics of ${\mathcal {P}}{\mathcal {T}}$-symmetric (pseudo-Hermitian) Hamiltonians [10, 11, 24]. Studies of pseudo-Hermitian operators carried out in [22, 23, 27] shows that, even if the eigenvalues of a Hamiltonian are real, the Riesz basis property of its eigenstates might be lost.

Such kind of phenomenon is typical for ${{\mathcal {P}}}{{\mathcal {T}}}$-symmetric Hamiltonians and it gives rise to a natural problem: How to generalize the Riesz basis to be suitable to the theory of pseudo-Hermitian Hamiltonians?

One of possible generalizations was proposed by Davies [13]: the concept of tame and wild sequences. Each basis is a tame sequence. The tameness of eigenstates of non self-adjoint operators H with a purely discrete real spectrum allows one to discover additional properties of H. In particular, a polynomially bounded behavior of the corresponding resolvent was established in [13, Theorem 3]. However, in major part, eigenstates of a pseudo-Hermitian Hamiltonian forms a wild system that is much more complicated for the investigation [13, 22, 23].

Another approach to the generalization of Riesz bases is based on the rigged Hilbert spaces framework instead of the original Hilbert space [9].

In the present paper, we study generalized Riesz systems (GRS) which were originally introduced in [17, 19] and then, slightly modified in [6, 8]. In order to explain the idea of definition we note that vectors of a Riesz basis $\{\phi _n\}$ have the form $\phi _n=Re_n$, where R is a bounded and boundedly invertible operator in a Hilbert space ${\mathcal {H}}$ and $\{e_n\}$ is an orthonormal basis (ONB) of ${\mathcal {H}}$. Using the polar decomposition of $R=|R^*|U=e^{Q/2}U$, where U is a unitary operator in ${\mathcal {H}}$, we conclude: a sequence$\{\phi _n\}$is called a Riesz basis if there exists a bounded self-adjoint operatorQin${\mathcal {H}}$and an ONB$\{e_n\}$such that$\phi _n=e^{Q/2}e_n$. This simple observation leads to:

Definition 1.1

A sequence $\{\phi _n\}$ is called a generalized Riesz system (GRS) if there exists a self-adjoint operator Q in ${\mathcal {H}}$ and an ONB $\{e_n\}$ such that $e_n\in {\mathcal {D}}(e^{Q/2})\cap {\mathcal {D}}(e^{-Q/2})$ and $\phi _n=e^{Q/2}e_n.$

For a GRS $\{\phi _n\}$, the dual GRS is determined by the formula $\{\psi _n=e^{-Q/2}e_n\}$. Obviously, $\{\phi _n\}$ and $\{\psi _n\}$ are bi-orthogonal sequences.

Dual GRS’s can be considered as a particular case of ${\mathcal {G}}$-quasi bases introduced by Bagarello in [4], and then analyzed in a series of papers, see, [7] and the references therein.

The main objective of the paper is further development of the GRS theory. In contrast to the standard approach [5, 6, 16,17,18,19], where GRS’s were mainly used as auxiliary tools for the definition and investigation of manifestly non self-adjoint Hamiltonians and relevant physical operators, we consider them as a self-contained object of the basis theory [12, 15]. Our studies are based on advanced methods of extension theory of symmetric operators, see [2, 3] and Sect. 2.1.

We say that a sequence of vectors $\{\phi _n\}$ in a Hilbert space ${\mathcal {H}}$ is semi-regular if $\{\phi _n\}$ is minimal and complete in ${\mathcal {H}}$. The minimality of $\{\phi _n\}$ yields the existence of a bi-orthogonal sequence $\{\psi _n\}$. The completeness of $\{\phi _n\}$ guarantees the uniqueness of $\{\psi _n\}$. The positive symmetric operator S that relates $\{\phi _n\}$ and $\{\psi _n\}$, see (2.4), plays an important role in our studies. We show that a semi-regular sequence $\{\phi _n\}$ is a GRS if and only if the Friedrichs extension $A_F$ of S is a positive operator (Theorem 2.5). It should be noted that our definition of semi-regular sequences is more general than the definition given by Inoue in [17]. We discuss this point in Remark 2.6.

Theorem 2.5 allows one to explain the nonuniqueness of self-adjoint operators Q in the definition of GRS (Sect. 2.3). Further we show that each semi-regular sequence $\{\phi _n\}$ with the property of being Bessel sequence has to be a GRS and we characterize this important case in terms of Q (Theorem 2.13). The Olevskii’s result [25, Theorem 1] allows one to establish a relationship between essential spectra of self-adjoint operators Q and conditional bounded bases (Proposition 2.14).

The end of Sect. 2 is devoted to an important particular case (which fits well the specific of ${{\mathcal {P}}}{{\mathcal {T}}}$-symmetric Hamiltonians) where a semi-regular sequence $\{\phi _n\}$ is J-orthonormal. Following [8], we define J-orthonormal sequences of the first/second type and discuss advantages of first type sequences. In particular, eigenstates of the shifted harmonic oscillator form a J-orthonormal sequence of the first type and it seems natural to suppose that eigenstates of a ${{\mathcal {P}}}{{\mathcal {T}}}$-symmetric Hamiltonian with unbroken ${{\mathcal {P}}}{{\mathcal {T}}}$-symmetry [10, p. 41] form a first type sequence. In Sect. 3.3 we describe a general method which allows one to construct of the first/second type sequences.

Throughout the paper, ${\mathcal {D}}(A)$, ${\mathcal {R}}(A)$, and $\ker {A}$ denote the domain, the range, and the null-space of a linear operator A, respectively. The symbol $\{u_n\}$ means the collection of vectors $u_n$ parametrized by a set ${\mathcal {I}}$ of integers. Usually, ${\mathcal {I}}={\mathbb {N}}$.

2 General Theory of GRS

2.1 Preliminaries

Here, all necessary results of extension theory of symmetric operators are presented in a form convenient for our exposition. The articles [1,2,3] and [26, Chap. 10] are recommended as complementary reading on the subject.

Let ${\mathcal {H}}$ be a complex Hilbert space with inner product $(\cdot , \cdot )$ linear in the first argument. An operator A is called positive [nonnegative] if $(Af,f)>0$ [$(Af,f)\ge {0}$] for non-zero $f\in {\mathcal {D}}(A)$.

Let A and B be nonnegative self-adjoint operators. We say that Ais greater or equalB, i.e., $A\ge {B}$ if

$$\begin{aligned} {\mathcal {D}}(A^{1/2})\subseteq {\mathcal {D}}(B^{1/2}) \quad \text{ and } \quad \Vert A^{1/2}f\Vert \ge \Vert B^{1/2}f\Vert , \quad f\in {\mathcal {D}}(A^{1/2}). \end{aligned}$$

(2.1)

The next technical result follows from (2.1) (see [26, Corollary 10.12]).

Lemma 2.1

If $A\ge {B}$ and B is positive, then A is also positive.

Let S be a nonnegative densely defined operator in ${\mathcal {H}}$. M. Krein established that the set of nonnegative self-adjoint extensions $\{A\}$ of S can be ordered as follows [3, Theorem 3.5]: $A_F\ge {A}\ge {A_K}$, where the greatest self-adjoint extension $A_F$ is called the Friedrichs extension, while the smallest one $A_K$ is called the Krein-von Neumann extension.

The extensions $A_K$ and $A_F$ are examples of extremal extensions. We recall [2] that a nonnegative self-adjoint extension A of S is called extremal if

$$\begin{aligned} \inf _{f\in {\mathcal {D}}(S)}{(A(\phi -f),(\phi -f))}=0 \quad \text{ for } \text{ all } \quad \phi \in {\mathcal {D}}(A). \end{aligned}$$

(2.2)

If a nonnegative self-adjoint extension A of S is positive, we can set $A=e^{-Q}$, where $Q=-\ln {A}$ is a self-adjoint operator in ${\mathcal {H}}$ and define the new Hilbert space ${\mathcal {H}}_{-Q}$ as the completion of ${\mathcal {D}}(A)={\mathcal {D}}(e^{-Q})$ with respect to the new inner product

$$\begin{aligned} (f, g)_{-Q}:=(e^{-Q}f, g)=(e^{-Q/2}f, e^{-Q/2}g), \qquad f,g\in {\mathcal {D}}(e^{-Q}). \end{aligned}$$

(2.3)

Rewriting (2.2) as

$$\begin{aligned} \inf _{f\in {\mathcal {D}}(S)}{(\phi -f, \phi -f)_{-Q}}=\inf _{f\in {\mathcal {D}}(S)}\Vert \phi -f\Vert _{-Q}^2=0 \quad \text{ for } \text{ all } \quad \phi \in {\mathcal {D}}(e^{-Q}) \end{aligned}$$

we obtain the following.

Lemma 2.2

A positive self-adjoint extension $A=e^{-Q}$ of S is an extremal extension if and only if ${\mathcal {D}}(S)$ is a dense set in ${\mathcal {H}}_{-Q}$.

A non-negative, non-densely defined symmetric operator S admits self-adjoint extensions, but not necessarily non-negative ones. The well-known Ando-Nishio result is [1, Theorem 1]:

Lemma 2.3

A closed non-negative symmetric operator S admits a non-negative self-adjoint extension if and only if it is positively closable, i.e., if the relations

$$\begin{aligned} \lim _{n\rightarrow \infty }(Sf_n, f_n)=0 \qquad \text{ and } \qquad \lim _{n\rightarrow \infty }Sf_n=g \end{aligned}$$

implies $g=0$.

Lemma 2.3 is obvious for densely defined operators because each densely defined operator S is positively closable [1, p. 67]. Another useful result follows from [1, Corollary 4]:

Lemma 2.4

Let S be a closed densely defined positive operator. Then the Friedrichs extension $A_F$ of S is positive if and only if $S^{-1}$ admits a non-negative self-adjoint extension.

2.2 Conditions of Being GRS

Let $\{\phi _n\}$ be a GRS. In view of Definition 1.1, the sequence $\{\psi _n=e^{-Q/2}e_n\}$ is well defined and it is a bi-orthogonal sequence for $\{\phi _n=e^{Q/2}e_n\}$. Obviously, $\{\psi _n\}$ is a GRS which we call a dual GRS.

The existence of a bi-orthogonal sequence means that each GRS $\{\phi _n\}$ has to be a minimal sequence, i.e., $\phi _j\notin {\overline{span}}{\{\phi _k\}_{k\not =j}}$ [12, Lemma 3.3.1]. However, not each minimal sequence is a GRS.

We say that a minimal sequence $\{\phi _n\}$ is semi-regular if $\{\phi _n\}$ is complete in ${\mathcal {H}}$ and regular if its bi-orthogonal sequence $\{\psi _n\}$ is also complete. For a semi-regular sequence $\{\phi _n\}$ the corresponding bi-orthogonal sequence $\{\psi _n\}$ is determined uniquely.

Let $\{\phi _n\}$ be a minimal sequence. Then there exists a bi-orthogonal sequence $\{\psi _n\}$ and we can consider an operator S defined initially on

$$\begin{aligned} S\phi _n=\psi _n, \end{aligned}$$

(2.4)

and extended on ${{\mathcal {D}}}(S)=span\{\phi _n\}$ by the linearity. By the construction,

$$\begin{aligned} (Sf, f)=\sum _{n=1}^k\sum _{m=1}^kc_n{\overline{c}}_m(\psi _n, \phi _m)=\sum _{n=1}^k{|c_n|^2} \quad \text{ for } \text{ all } \quad f=\sum _{n=1}^k{c_n}\phi _n\in {{\mathcal {D}}(S)}. \end{aligned}$$

Therefore, S is a positive operator. For a semi-regular sequence $\{\phi _n\}$, the operator S is densely defined and the Friedrichs extension $A_F$ of S exists.

Theorem 2.5

Let $\{\phi _n\}$ be a semi-regular sequence. The following are equivalent:

• (i) $\{\phi _n\}$ is a GRS;

• (ii) the Friedrichs extension $A_F$ of S is a positive operator;

• (iii) the closure ${\overline{S}}$ of S is a positive operator and the relations

  $$\begin{aligned} \lim _{n\rightarrow \infty }({\overline{S}}f_n, f_n)=0 \qquad \text{ and } \qquad \lim _{n\rightarrow \infty }f_n=g \end{aligned}$$

  (2.5)

  imply that $g=0$;

• (iv) the set $D(\phi )=\{f\in {\mathcal {H}} \ : \ \sum _{n=1}^\infty |(f, \phi _n)|^2<\infty \}$ is dense in ${\mathcal {H}}$.

Proof

$\mathrm{(i)}\rightarrow \mathrm{(ii)}$ If $\{\phi _n\}$ is a GRS, then $e^{-Q}\phi _n=e^{-Q/2}e_n=\psi _n$. In view of (2.4), $e^{-Q}$ is a positive self-adjoint extension of S and $A_F\ge {e^{-Q}}$ since the Friedrichs extension is the greatest nonnegative self-adjoint extension of S. By virtue of Lemma 2.1, $A_F$ is positive.

$\mathrm{(ii)}\rightarrow \mathrm{(i)}$ The positivity of $A_F$ means that $A_F=e^{-Q}$, where Q is a self-adjoint operator in ${\mathcal {H}}$. Denote $e_n=e^{-Q/2}\phi _n$. Due to (2.4), $e_n=e^{Q/2}\psi _n$. Therefore, $e_n\in {\mathcal {D}}(e^{Q/2})\cap {\mathcal {D}}(e^{-Q/2})$ and $(e_n, e_m)=(e^{-Q/2}\phi _n, e^{Q/2}\psi _m)=(\phi _n, \psi _m)=\delta _{nm}$.

The orthonormal sequence $\{e_n\}$ turns out to be an ONB if $\{e_n\}$ is complete in ${\mathcal {H}}$. Assume that $\gamma$ is orthogonal to $\{e_n\}$ in ${\mathcal {H}}$. Then there exists a sequence $\{f_m\}$$(f_m\in {\mathcal {D}}(e^{-Q}))$ such that $e^{-Q/2}{f_m}\rightarrow \gamma$ in ${\mathcal {H}}$ (because $e^{-Q/2}{\mathcal {D}}(e^{-Q})$ is a dense set in ${\mathcal {H}}$). In this case, due to (2.3), $\{f_m\}$ is a Cauchy sequence in ${\mathcal {H}}_{-Q}$ and therefore, ${f}_m$ tends to some $f\in {\mathcal {H}}_{-Q}$. This means that

$$\begin{aligned} 0=(\gamma , e_n)=\lim _{m\rightarrow \infty }(e^{-Q/2}{f_m}, e_n)=\lim _{m\rightarrow \infty }(f_m, \phi _n)_{-Q}=(f, \phi _n)_{-Q}. \end{aligned}$$

(2.6)

By Lemma 2.2, the set ${\mathcal {D}}(S)=span\{\phi _n\}$ is dense in the Hilbert space ${\mathcal {H}}_{-Q}$. Due to (2.6), $f=0$ that means $\lim _{m\rightarrow \infty }\Vert f_m\Vert _{-Q}=\lim _{m\rightarrow \infty }\Vert e^{-Q/2}f_m\Vert =0$ and hence, $\gamma =0$. Thus, $\{e_n\}$ is complete in ${\mathcal {H}}$ and $\{e_n\}$ is an ONB of ${\mathcal {H}}$.

The implication $\mathrm{(ii)}\rightarrow \mathrm{(iii)}$ is obvious.

$\mathrm{(iii)}\rightarrow \mathrm{(ii)}$ The operator ${\overline{S}}$ has the inverse ${{\overline{S}}}^{-1}$ since ${\overline{S}}$ is positive. The operator ${{\overline{S}}}^{-1}$ is closed and (2.5) can be rewritten as follows:

$$\begin{aligned} \lim _{n\rightarrow \infty }(g_n, {{\overline{S}}}^{-1}g_n)=0 \qquad \text{ and } \qquad \lim _{n\rightarrow \infty }{{\overline{S}}}^{-1}g_n=g \qquad (g_n={\overline{S}}f_n) \end{aligned}$$

This means that ${{\overline{S}}}^{-1}$ is positively closable. Hence, it admits a non-negative self-adjoint extension (Lemma 2.3) Applying Lemma 2.4 we complete the proof of $\mathrm{(iii)}\rightarrow \mathrm{(ii)}$.

The implication $\mathrm{(i)}\rightarrow \mathrm{(iv)}$ follows from the fact that ${\mathcal {R}}(e^{-Q/2})\subset {D(\phi )}$ since, for all $u\in {\mathcal {D}}(e^{-Q/2})$,

$$\begin{aligned} \sum _{n=1}^\infty |(e^{-Q/2}u, \phi _n)|^2=\sum _{n=1}^\infty |(u, e^{-Q/2}\phi _n)|^2=\sum _{n=1}^\infty |(u, e_n)|^2=\Vert u\Vert ^2<\infty . \end{aligned}$$

$\mathrm{(iv)}\rightarrow \mathrm{(ii)}$ Following [17] we consider the densely defined operators

$$\begin{aligned} T_{e\phi }f=\sum _{n=1}^\infty (f, \phi _n)e_n, \quad {\mathcal {D}}(T_{e\phi })=D(\phi ), \qquad T_{\phi {e}}g=\sum _{n=1}^\infty (g, e_n)\phi _n, \end{aligned}$$

${\mathcal {D}}(T_{\phi {e}})=\{g\in {\mathcal {H}} : \ \text{ the } \text{ series } \ \sum _{n=1}^\infty (g, e_n)\phi _n \ \text{ converges } \text{ in } \ {\mathcal {H}}\}$.

It is easy to see that $T_{e\phi }$ is a closable operator and $\ker {\overline{T}}_{e\phi }=\{0\}$, where ${\overline{T}}_{e\phi }$ is the closure of $T_{e\phi }$. Therefore, the operator $B=T_{e\phi }^*{\overline{T}}_{e\phi }$ is positive self-adjoint in ${\mathcal {H}}$. Here $T_{e\phi }^*\supset {T_{\phi {e}}}$, since $(T_{e\phi }f, g)=(f, T_{\phi {e}}g)$ for $f\in {\mathcal {D}}(T_{e\phi })$ and $g\in {\mathcal {D}}(T_{\phi {e}})$. Taking into account that $T_{e\phi }\psi _n=e_n$ and $T_{\phi {e}}e_n=\phi _n$, we obtain $B\psi _n=\phi _n$. Hence, B is a positive self-adjoint extension of $S^{-1}$. This means that $A=B^{-1}$ is a positive self-adjoint extension of S and, in view of Lemma 2.1, the Friedrichs extension $A_F$ of S is also a positive operator. $\square$

Remark 2.6

The item (iv) of Theorem 2.5 was proved in [17] [item (2) of Theorem 3.4]. The definition of a semi-regular sequence $\{\phi _n\}$ given in [17] (Definition 3.3) involves the condition (iv) as an additional assumption. For this reason each Inoue’s semi-regular sequence $\{\phi _n\}$ has to be a GRS.

It is worth mentioning that the example of semi-regular sequence $\{\phi _n\}$ given in [17] after Definition 3.3 may be misleading because $\{\phi _n\}$ is not a semi-regular sequence in the sense of [17] and it cannot be a GRS. Indeed, the sequence $\{\phi _n\}$ is defined as $\phi _n={\mathsf {e}}_n+{\mathsf {e}}_0$, $n=1,2\ldots$, where $\{{\mathsf {e}}_n\}_{n=0}^{\infty }$ is an ONB of ${\mathcal {H}}$. It is easy to see that $\{\phi _n\}$ is complete in ${\mathcal {H}}$ and $\{\phi _n\}$ is minimal (since there exists a bi-orthogonal sequence $\{\psi _n={\mathsf {e}}_n\}_{n=1}^\infty$). If $f=\sum _{n=0}^\infty {f_n}e_n$ belongs to $D(\phi )$, then $\sum _{n=1}^\infty |(f, \phi _n)|^2=\sum _{n=1}^\infty |f_n+f_0|^2<\infty$. The last inequality is possible only for the case $f_0=0$. Therefore, the vector ${\mathsf {e}}_0$ is orthogonal to $D(\phi )$. A generalization of this example is considered in Sect. 3.1.

Corollary 2.7

A regular sequence is a GRS.

Proof

Let $\{\phi _n\}$ be a regular sequence. Its regularity means that ${\mathcal {R}}(S)$ is a dense set in ${\mathcal {H}}$. The latter means that each nonnegative self-adjoint extension A of S must be positive. In particular, the Friedrichs extension $A_F$ is positive. By Theorem 2.5, $\{\phi _n\}$ is a GRS. $\square$

A shifting of the orthonormal Hermite functions $e_n(x)$ in the complex plane gives rise to regular sequences in $L_2({\mathbb {R}})$. In particular, eigenfunctions of the shifted harmonic oscillator $\{\phi _n(x)=e_n(x+ia)\}$ form a regular sequence and $\phi _n=e^{Q/2}e_n$, where $Q=2ai\frac{d}{dx}$ is an unbounded self-adjoint operator in $L_2({\mathbb {R}})$ [8, Subsection IV.1]. We refer [16, 19] to the relationship between general regular sequences and some physical operators.

Remark 2.8

Theorem 2.5 can be generalized to the case of non-complete minimal sequence $\{\phi _n\}$ such that its bi-orthogonal $\{\psi _n\}$ is also non-complete. In this case, S is a non-densely defined positive symmetric operator in ${\mathcal {H}}$. We should suppose the existence of a positive self-adjoint extension A of S. Similarly to the proof of Theorem  2.5 we set $A=e^{-Q}$ and determine the orthonormal system $\{e_n\}$ in ${\mathcal {H}}$. By virtue of (2.6), the completeness of $\{e_n\}$ in ${\mathcal {H}}$ is equivalent to the completeness of $\{\phi _n\}$ in ${\mathcal {H}}_{-Q}$. This means that $\{e_n\}$ is an ONB of ${\mathcal {H}}$ if and only if $\{\phi _n\}$ is complete in ${\mathcal {H}}_{-Q}$. Summing up: Let$\{\phi _n\}$be a minimal sequence and let$\{\psi _n\}$be its bi-orthogonal sequence. These sequences are GRS if and only if there exists a positive self-adjoint extension$A=e^{-Q}$ofSsuch that$\{\phi _n\}$is a complete set in the Hilbert space${\mathcal {H}}_{-Q}$.

Another approach to the study of non-complete minimal sequences can be found in [6].

2.3 The Uniqueness of Q in the Definition of GRS

Let $\{\phi _n\}$ be a basis in ${\mathcal {H}}$. Then $\{\phi _n\}$ is a regular sequence because its bi-orthogonal sequence $\{\psi _n\}$ has to be a basis [15, Corollary 5.22]. By Corollary 2.7, $\{\phi _n\}$ is a GRS, i.e., $\phi _n=e^{Q/2}e_n$. Moreover, by [8, Proposition II.9], the pair $(Q, \{e_n\})$ in Definition 1.1 is determined uniquely for every basis $\{\phi _n\}$. For this reason, a natural question arise: is the pair$(Q, \{e_n\})$determined uniquely for a given GRS$\{\phi _n\}$?

The choice of the Friedrichs extension $A_F=e^{-Q}$ of S in the proof of Theorem 2.5 was related to the fact that ${\mathcal {D}}(S)$ must be dense in the Hilbert space ${\mathcal {H}}_{-Q}$ (that, in view of (2.6), is equivalent to the completeness of $\{e_n\}$ in ${\mathcal {H}}$). Due to Lemma 2.2, each positive extremal extension $A=e^{-Q}$ can be used instead of $A_F$ in the proof of Theorem 2.5. This observation leads to the following result ([8, Proposition II.10]):

Proposition 2.9

Let a semi-regular sequence $\{\phi _n\}$ be a GRS. Then a self-adjoint operator Q and an ONB $\{e_n\}$ are determined uniquely in the formula $\phi _n=e^{Q/2}e_n$ if and only the symmetric operator S in (2.4) has a unique positive extremal extension.

Remark 2.10

The above mentioned unique positive extremal extension coincides with the Friedrichs extension $A_F$. Indeed, the existence of another positive extension $A\not =A_F$ means that $A_F$ is also positive (Lemma 2.1). Due to the uniqueness of positive extension, we get $A=A_F$.

2.4 Bases and Bessel Sequences

Various classes of GRS’s can be easily characterized in terms of spectral properties of the corresponding self-adjoint operators Q.

We recall that a semi-regular sequence $\{\phi _n\}$ is called a Riesz basis if there exists $0<a\le {b}$ such that¹

$$\begin{aligned} {a}\Vert f\Vert ^2\le \sum _{n}|(f, \phi _n)|^2\le {b}\Vert f\Vert ^2 \quad \text{ for } \text{ all } \quad f\in {\mathcal {H}}. \end{aligned}$$

(2.7)

Proposition 2.11

The following are equivalent:

• (i) a sequence $\{\phi _n\}$ is a Riesz basis with bounds $0<a\le {b}$;

• (ii) $\{\phi _n\}$ is a GRS, i.e., $\phi _n=e^{Q/2}e_n$, where Q is a bounded self-adjoint operator such that $\sigma (Q)\subset [\ln {a}, \ln {b}]$.

Proof

If $\{\phi _n\}$ is a Riesz basis, then $\phi _n=e^{Q/2}e_n$, where Q is a bounded operator (see Sect. 1). The substitution of $\phi _n=e^{Q/2}e_n$ into (2.7) gives

$$\begin{aligned} a(f,f)={a}\Vert f\Vert ^2\le \sum _{n}|(e^{Q/2}f, e_n)|^2\le \Vert e^{Q/2}f\Vert ^2=(e^Qf, f)\le {b}\Vert f\Vert ^2=b(f,f). \end{aligned}$$

Therefore, $aI\le {e^Q}\le {bI}$ that justifies $\mathrm{(i)}\rightarrow \mathrm{(ii)}$. The converse statement is obvious. $\square$

Lemma 2.12

Let Q be a self-adjoint operator such that $\sigma (Q)\subset (-\infty , \ln {b}]$ and let $\{e_n\}$ be an arbitrary ONB of ${\mathcal {H}}$. Then the sequence $\{\phi _n=e^{Q/2}e_n\}$ is a GRS with the pair $(Q, \{e_n\})$.

Proof

Since $\sigma (Q)\subset (-\infty , \ln {b}]$, the self-adjoint operator $e^{Q/2}$ is bounded. Hence, the elements $\phi _n=e^{Q/2}e_n$ are well-defined. If $\gamma$ is orthogonal to $\{\phi _n\}$, then $0=(\gamma , e^{Q/2}e_n)=(e^{Q/2}\gamma , e_n)$ implies that $e^{Q/2}\gamma =\gamma =0$. Therefore $\{\phi _n\}$ is semi-regular and its bi-orthogonal sequence $\{\psi _n\}$ is defined uniquely. According to Definition 1.1, it is sufficient to show that $e_n\in {\mathcal {D}}(e^{-Q/2})$ and $\psi _n=e^{-Q/2}e_n$. By virtue of the relation $\delta _{mn}=(\phi _m, \psi _n)=(e^{Q/2}e_m, \psi _n)=(e_m, e^{Q/2}\psi _n)$ we obtain that $e^{Q/2}\psi _n=e_n$ . The last relation means that $e_n\in {\mathcal {D}}(e^{-Q/2})$ and $\psi _n=e^{-Q/2}e_n$. $\square$

A sequence $\{\phi _n\}$ is called a Bessel sequence if there exists $b>0$ such that

$$\begin{aligned} \sum _{n}|(f, \phi _n)|^2\le {b}\Vert f\Vert ^2 \quad \text{ for } \text{ all } \quad f\in {\mathcal {H}}. \end{aligned}$$

(2.8)

Theorem 2.13

The following are equivalent:

• (i) a semi-regular sequence $\{\phi _n\}$ is a Bessel sequence;

• (ii) $\{\phi _n\}$ is a GRS, i.e., $\phi _n=e^{Q/2}e_n$, where Q is a self-adjoint operator such that $\sigma (Q)\subset (-\infty , \ln {b}]$.

Proof

$\mathrm{(i)}\rightarrow \mathrm{(ii)}$ If $\{\phi _n\}$ is a Bessel sequence, then the synthesis operator $R\{c_n\}=\sum {c_n\phi _n}$ defines a bounded operator which maps $l^2({\mathbb {N}})$ into ${\mathcal {H}}$ [15, p. 190]. The minimality of $\{\phi _n\}$ implies that $\{\phi _n\}$ is $\omega$-independent [15, p. 156]. The latter means that the series $\sum {c_n\phi _n}$ converges and equal 0 only when $c_n=0$. Therefore, $\ker {R}=\{0\}$.

Let $\{\delta _n\}$ be the canonical basis of $l^2({\mathbb {N}})$. Then $R\delta _n=\phi _n$. Identifying $\{\delta _n\}$ with an ONB $\{{\tilde{e}}_n\}$ of ${\mathcal {H}}$ we obtain a bounded operator²R in ${\mathcal {H}}$ such $R{\tilde{e}}_n=\phi _n$. The polar decomposition of R is $R=|R^*|U$, where $|R^*|=\sqrt{RR^*}$ and U is an isometric operator mapping the closure of ${{\mathcal {R}}}(\sqrt{R^*R})$ onto the closure of ${{\mathcal {R}}}(R)$ [21, Chapter VI, Subsect. 2.7]. We remark that ${{\mathcal {R}}}(\sqrt{R^*R})$ and ${{\mathcal {R}}}(R)$ are dense sets in ${\mathcal {H}}$, since, respectively, $\ker \sqrt{R^*R}=\ker {R}=\{0\}$ and $\{\phi _n\}$ is a complete set in ${\mathcal {H}}$. Therefore, U is a unitary operator in ${\mathcal {H}}$. Moreover, $|R^*|$ is a positive bounded self-adjoint operator (since $\ker |R^*|=\ker {R}=\{0\}$). The positivity of $|R^*|$ leads to the formula $|R^*|=e^{Q/2}$, where Q is a self-adjoint operator in ${\mathcal {H}}$. Denote $e_n=U{\tilde{e}}_n$. Obviously, $\{e_n\}$ is an ONB of ${\mathcal {H}}$ and

$$\begin{aligned} \phi _n=R{\tilde{e}}_n=|R^*|U{\tilde{e}}_n=e^{Q/2}U{\tilde{e}}_n=e^{Q/2}e_n. \end{aligned}$$

After the substitution of $\phi _n=e^{Q/2}e_n$ into (2.8),

$$\begin{aligned} \sum _{n}|(f, e^{Q/2}e_n|^2=\sum _{n}|(e^{Q/2}f, e_n|^2=\Vert e^{Q/2}f\Vert ^2=(e^{Q}f, f)\le {b}(f, f). \end{aligned}$$

The obtained inequality leads to the conclusion that $\sigma (Q)\subset (-\infty , \ln {b}]$. Applying Lemma 2.12 we complete the proof of $\mathrm{(i)}\rightarrow \mathrm{(ii)}$.

$\mathrm{(ii)}\rightarrow \mathrm{(i)}$ In view of Lemma 2.12, $\{\phi _n\}$ is a semi-regular sequence. The operator $e^Q$ is bounded and $\Vert e^Q\Vert \le {b}$ (since $\sigma (Q)\subset (-\infty , \ln {b}]$). Hence,

$$\begin{aligned} \sum _{n}|(f, \phi _n)|^2= \sum _{n}|(e^{Q/2}f, e_n|^2=\Vert e^{Q/2}f\Vert ^2=(e^{Q}f, f)\le {b}\Vert f\Vert ^2 \end{aligned}$$

that completes the proof. $\square$

A sequence $\{\phi _n\}$ is called bounded if $0<a\le \Vert \phi _n\Vert \le {b}$ for all n. A basis $\{\phi _n\}$ is called conditional if its property of being basis depends on the permutation of elements $\phi _n$.

Proposition 2.14

Let Q be a self-adjoint operator in ${\mathcal {H}}$ such that $\sigma (Q)\subset (-\infty , \ln {b}]$. The following are equivalent:

• (i) there exists an ONB $\{e_n\}$ of ${\mathcal {H}}$ such that the sequence $\{\phi _n=e^{Q/2}e_n\}$ is a conditional bounded basis;

• (ii) there exists $\beta <0$ such that each interval $[(n+1)\beta , n\beta ]$ ($n=0,1,\ldots$) includes at least one point of essential spectrum of Q.

Proof

Applying [25, Theorem 1] to the positive bounded operator $e^{Q/2}$ and taking into account properties of an essential spectrum [26, Proposition 8.11] we arrive at the conclusion that the item $\mathrm{(i)}$ is equivalent to the existence of $0<q<1$ such that the essential spectrum of $e^{Q/2}$ has a non-zero interaction with each interval $[q^{n+1}, q^n]$. Since $Q=2\ln {e^{Q/2}}$, the later statement is equivalent to $\mathrm{(ii)}$ with $\beta =2\ln {q}$. $\square$

Let ${\mathcal {H}}=L_2(-\pi , \pi )$ and Q is an operator of multiplication by $\alpha \ln |x|$ ($0<\alpha$) in ${\mathcal {H}}$. Obviously, Q is self-adjoint, its spectrum coincides with $(-\infty , \ln {\pi ^\alpha }]$ and it is essential. By Proposition 2.14, there exists an ONB $\{e_n\}$ of $L_2(-\pi , \pi )$ such that $\{\phi _n=e^{Q/2}e_n\}$ is a conditional bounded basis. In view of the Babenko example [15, Example 5.13], for $0<\alpha <\frac{1}{2}$, the corresponding ONB can be chosen as $\{e_n=\frac{1}{\sqrt{2\pi }}e^{inx}\}_{-\infty }^\infty$.

2.5 J-Orthonormal Sequences and GRS

Let J be a bounded self-adjoint operator in a Hilbert space ${\mathcal {H}}$ such that $J^2=I$. The Hilbert space ${\mathcal {H}}$ equipped with the indefinite inner product $[\cdot , \cdot ]:=(J\cdot , \cdot )$ is called a Krein space.

A sequence $\{\phi _n\}$ is called J-orthonormal if $|[\phi _n, \phi _m]|=\delta _{nm}$.

Each J-orthonormal sequence $\{\phi _n\}$ is minimal since its bi-orthogonal one is determined as

$$\begin{aligned} \psi _n=[\phi _n,\phi _n]J\phi _n. \end{aligned}$$

(2.9)

In view of (2.9), the positive symmetric operator S in (2.4) acts as $S\phi _n=[\phi _n, \phi _n]J\phi _n$.

Proposition 2.15

Let $\{\phi _n\}$ be a complete J-orthonormal sequence. Then $\{\phi _n\}$ is a Bessel sequence if and only if $\{\phi _n\}$ is a Riesz basis.

Proof

Let us assume that $\{\phi _n\}$ is a Bessel sequence. Then $\{\psi _n\}$ is also a Bessel sequence. Indeed, substituting Jf instead of f into (2.8) and using (2.9), we obtain

$$\begin{aligned} \sum _{n}|(Jf, \phi _n)|^2=\sum _{n}|(f, J\phi _n)|^2=\sum _{n}|(f, \psi _n)|^2\le {b}\Vert Jf\Vert ^2=b\Vert f\Vert ^2. \end{aligned}$$

Due to Theorem 2.13, $\{\phi _n\}$ is a GRS and $\phi _n=e^{Q/2}e_n$, where $\sigma (Q)\subset (-\infty , \ln {b}]$. Since $\{\psi _n\}$ is also a Bessel sequence, applying Theorem 2.13 again we obtain $\sigma (-Q)\subset (-\infty , \ln {b}]$ or $\sigma (Q)\subset [-\ln {b}, \infty )$. Therefore, $\sigma (Q)\subset [\ln {a}, \ln {b}]$, where $a=1/b$. In view of Proposition 2.11, $\{\phi _n\}$ is a Riesz basis. The inverse statement is obvious. $\square$

If $\{\phi _n\}$ is complete in ${\mathcal {H}}$, then $\{\psi _n\}$ in (2.9) is complete too. Therefore, $\{\phi _n\}$ is regular and, by Corollary 2.7, $\{\phi _n\}$ is a GRS. Thus, each complete J-orthonormal sequence is a GRS.

It follows from the proof of Corollary 2.7 that each extremal extension A of S is positive. Therefore, the corresponding operator $Q=-\ln A$ in Definition 1.1 can be determined by every extremal extension A. If Q is determined uniquely, then [8, Theorem III.3]:

$$\begin{aligned} JQ=-QJ. \end{aligned}$$

(2.10)

However, if Q is not determined uniquely, not each $Q=-\ln {A}$ satisfies (2.10). In particular, as follows from [20], the operator Q that corresponds to the Friedrichs extension $A_F$ does not satisfy (2.10). Moreover, there exist complete J-orthonormal sequences for which no operators Q satisfying (2.10) can be found.

We say that a completeJ-orthonormal sequence$\{\phi _n\}$is of the first type if there exists a self-adjoint operator Q in Definition 1.1 such that (2.10) holds. Otherwise, $\{\phi _n\}$ is of the second type.

J-orthonormal bases are examples of the first type sequences. The next statement was proved in [20], where the notation “quasi-bases” was used for the first type sequences.

Proposition 2.16

The following are equivalent:

• (i) a complete J-orthonormal sequence $\{\phi _n\}$ is of the first type;

• (ii) the sequence $\{\phi _n\}$ is regular and the corresponding pair $(Q, \{e_n\})$ in Definition 1.1 can be chosen as follows: Q satisfies (2.10) and $e_n$ are eigenfunctions of J, i.e., $Je_n=e_n$ or $Je_n=-e_n$.

In what follows, by considering a first type sequence $\{\phi _n=e^{Q/2}e_n\}$, we assume that the pair $(Q, \{e_n\})$ satisfies conditions $\mathrm{(ii)}$ of Proposition 2.16. A detailed analysis of the first/second type sequences can be found in [8]. We just mention that a first type sequence $\{\psi _n=e^{Q/2}e_n\}$ generates a ${\mathcal {C}}$-symmetry operator³${\mathcal {C}}=e^QJ$ with the same operator Q. The latter allows one to construct the new Hilbert space ${\mathcal {H}}_{-Q}$ involving $\{\phi _n\}$ as ONB, directly as the completion of ${\mathcal {D}}({\mathcal {C}})$ with respect to “${\mathcal {C}}{{\mathcal {P}}}{{\mathcal {T}}}$-norm”: $(\cdot , \cdot )_{-Q}=[{\mathcal {C}}\cdot , \cdot ]=(Je^QJ\cdot ,\cdot )=(e^{-Q}\cdot , \cdot ).$

For a second type sequence, the inner product $(\cdot ,\cdot )_{-Q}$ defined by (2.3) cannot be expressed via $[\cdot , \cdot ]$ and one should apply much more efforts for the precise definition of $(\cdot ,\cdot )_{-Q}$.

3 Examples

3.1 A Semi-regular Sequence that Cannot be a GRS

Let $\{{\mathsf {e}}_n\}_{n=0}^{\infty }$ be an ONB of ${\mathcal {H}}$. Denote

$$\begin{aligned} \phi _n=\frac{1}{n^\beta }{\mathsf {e}}_n+\frac{1}{n^\alpha }{\mathsf {e}}_0, \qquad \alpha , \beta \in {\mathbb {R}}, \quad n=1,2,\ldots \end{aligned}$$

The sequence $\{\phi _n\}_{n=1}^\infty$ is minimal since $\{\psi _n=n^{\beta }{\mathsf {e}}_n\}_{n=1}^\infty$ is bi-orthogonal to $\{\phi _n\}$. It is easy to see that $\{\phi _n\}$ is complete in ${\mathcal {H}}$ if and only if $\alpha -\beta \le \frac{1}{2}$. The last relation determines admissible parameters $\alpha , \beta$ for which $\{\phi _n\}$ is a semi-regular sequence. Throughout Sect. 3.1 we suppose that this inequality holds.

In view of (2.4), $S(\frac{1}{n^\beta }{\mathsf {e}}_n+\frac{1}{n^\alpha }{\mathsf {e}}_0)=n^{\beta }{\mathsf {e}}_n$ and the operator S can be described as:

$$\begin{aligned} Sf=\sum _{n=1}^k{n^{2\beta }}c_n{\mathsf {e}}_n \quad \text{ for } \text{ all } \quad f=\sum _{n=1}^k{c_n}{\mathsf {e}}_n+\left( \sum _{n=1}^k\frac{n^{\beta }c_n}{n^{\alpha }}\right) {\mathsf {e}}_0 \ \in {\mathcal {D}}(S). \end{aligned}$$

(3.1)

It follows from (3.1) that the non-negative self-adjoint operator

$$\begin{aligned} Af=A\left( \sum _{n=0}^\infty {c}_n{\mathsf {e}}_n\right) =\sum _{n=1}^\infty {n^{2\beta }}c_n{\mathsf {e}}_n \end{aligned}$$

(3.2)

with the domain ${\mathcal {D}}(A)=\left\{ f=\sum _{n=0}^\infty {c_n}{\mathsf {e}}_n : \{c_n\}_{n=1}^\infty , \{n^{2\beta }c_n\}_{n=1}^\infty \in {\ell _2({\mathbb {N}})}\right\}$ is an extension of S.

If $\beta \le {0}$, then the semi-regular sequence $\{\phi _n\}$ cannot be a GRS. Indeed, in this case, the operator A is bounded. Therefore, A coincides with the closure ${\overline{S}}$ of S. In view of (3.2), ${\overline{S}}{\mathsf {e}}_0=A{\mathsf {e}}_0=0$. By Theorem 2.5, $\{\phi _n\}$ cannot be a GRS.

Assume now that $\beta >0$. Then A is an unbounded non-negative self-adjoint extension of S. Hence, A is an extension of ${\overline{S}}$. Using (3.1) and (3.2), we obtain that $f=\sum _{n=0}^\infty {c_n}{\mathsf {e}}_n$ belongs to ${\mathcal {D}}({\overline{S}})$ if and only if

$$\begin{aligned} \{c_n\},\ \{n^{2\beta }c_n\}\in \ell _2({\mathbb {N}}), \ \text{ the } \text{ series } \ \sum _{n=1}^\infty \frac{n^{\beta }c_n}{n^{\alpha }} \ \text{ converges } \text{ and } \ c_0=\sum _{n=1}^\infty \frac{n^{\beta }c_n}{n^{\alpha }}. \end{aligned}$$

Since $({\overline{S}}f,f)=\sum _{n=1}^\infty {n^{2\beta }}|c_n|^2$, the operator ${\overline{S}}$ is positive. Using statement (iii) of Theorem 2.5 we show that the semi-regular sequence $\{\phi _n\}$ is a GRS for $\alpha >\frac{1}{2}$. To that end, it suffices to verify the implication (2.5).

Let ${f_m=\sum _{n=0}^\infty {c_n^m}{\mathsf {e}}_n}$ be a sequence of elements $f_m\in {\mathcal {D}}({\overline{S}})$ satisfying (2.5). Then

$$\begin{aligned} \lim _{m\rightarrow \infty }({\overline{S}}f_m, f_m)=\lim _{m\rightarrow \infty }\sum _{n=1}^\infty {n^{2\beta }}|c_n^m|^2=\Vert \{n^{\beta }c_n^m\}\Vert ^2_{\ell _2({\mathbb {N}})}=0 \end{aligned}$$

and, since $\{{1}/{n^{\alpha }}\}\in \ell _2({\mathbb {N}})$ for $\alpha >\frac{1}{2}$,

$$\begin{aligned} g= & {} \lim _{m\rightarrow \infty }f_m=\lim _{m\rightarrow \infty }\sum _{n=1}^\infty {c_n^m}{\mathsf {e}}_n+ \lim _{m\rightarrow \infty }\sum _{n=1}^\infty \frac{n^{\beta }c_n^m}{n^{\alpha }}{\mathsf {e}}_0 \nonumber \\= & {} \lim _{m\rightarrow \infty }(\{n^{\beta }c_n^m\}, \{1/{n^{\alpha }}\})_{\ell _2({\mathbb {N}})}{\mathsf {e}}_0=0 \end{aligned}$$

(3.3)

that justifies the implication (2.5).

3.2 A Semi-regular Bessel Sequence

Let $\{{\mathsf {e}}_n\}_{{\mathbb {Z}}}$ be an ONB of ${\mathcal {H}}$. Denote $\phi _n=K{\mathsf {e}}_n, \ n\in {\mathbb {Z}}\setminus \{0\}$, where K is a bounded operator in ${\mathcal {H}}$. The sequence $\{\phi _n\}_{{\mathbb {Z}}\setminus \{0\}}$ is a Bessel sequence since

$$\begin{aligned} \sum _{n\not =0}|(f, \phi _n)|^2=\sum _{n\not =0}|(K^*f, {\mathsf {e}}_n)|^2\le \Vert K^*f\Vert ^2\le \Vert K^*\Vert ^2\Vert f\Vert ^2. \end{aligned}$$

Proposition 3.1

The following are equivalent:

• (i) $\{\phi _n\}$ is semi-regular in ${\mathcal {H}}$;

• (ii) $\ker K^*=\{0\}$ and there exists a unique sequence of numbers $\{\alpha _n\}_{{\mathbb {Z}}\setminus \{0\}}$ such that ${\mathsf {e}}_n-\alpha _n{\mathsf {e}}_0\in {\mathcal {R}}(K^*)$.

Proof

$\mathrm{(i)}\rightarrow \mathrm{(ii)}$ In view of the equality $(h, \phi _n)=(K^*h, {\mathsf {e}}_n)$ where $n\in {\mathbb {Z}}\setminus \{0\}$, the completeness of $\{\phi _n\}$ is equivalent to the conditions: $\ker K^*=\{0\}$ and ${\mathsf {e}}_0\not \in {\mathcal {R}}(K^*)$. Let $\{\psi _n\}$ be the bi-orthogonal sequence for $\{\phi _n\}$. Then

$$\begin{aligned} \delta _{nm}=(\phi _n, \psi _m)=({\mathsf {e}}_n, K^*\psi _m) \end{aligned}$$

that means $K^*\psi _m={\mathsf {e}}_m+\alpha _m{\mathsf {e}}_0$, where $\alpha _m$ is determined uniquely (since ${\mathsf {e}}_0\not \in {\mathcal {R}}(K^*)$).

$\mathrm{(ii)}\rightarrow \mathrm{(i)}$ The vector ${\mathsf {e}}_0$ does not belong to ${\mathcal {R}}(K^*)$ since the sequence $\{\alpha _n\}$ is determined uniquely in the relation ${\mathsf {e}}_n-\alpha _n{\mathsf {e}}_0\in {\mathcal {R}}(K^*)$. This fact and $\ker K^*=\{0\}$ give the completeness of $\{\phi _n\}$ in ${\mathcal {H}}$. The minimality of $\{\phi _n\}$ follows from the fact that $\{\psi _n={K^*}^{-1}({\mathsf {e}}_n-\alpha _n{\mathsf {e}}_0)\}$ is a bi-orthogonal sequence for $\{\phi _n\}$. $\square$

In view of Theorem 2.13, the sequence $\{\phi _n\}$ is a GRS if and only if the condition $\mathrm{(ii)}$ of Proposition 3.1 holds. In this case, $\{\phi _n=e^{Q/2}e_n\}_{{\mathbb {Z}}\setminus \{0\}}$, where Q is a self-adjoint operator such that $\sigma (Q)\subset (-\infty , 2\ln \Vert K\Vert ]$ and $\{e_n\}_{{\mathbb {Z}}\setminus \{0\}}$ is an ONB of ${\mathcal {H}}$.

In the space ${\mathcal {H}}=L_2(0,1)$, the operator $Kf=x^Nf(x)$ ($N\in {\mathbb {N}}$) is bounded. Consider the sequence $\{\phi _n=x^N{\mathsf {e}}_n\}_{{\mathbb {Z}}\setminus \{0\}}$, where $\{{\mathsf {e}}_n=e^{2\pi {i}nx}\}_{\mathbb {Z}}$ is the trigonometric ONB of ${\mathcal {H}}=L_2(0,1)$. It is easy to see that the condition $\mathrm{(ii)}$ of Proposition 3.1 holds for $N=1$ only (then $\alpha _n=1$ for all $n\in {\mathbb {Z}}\setminus \{0\}$). Therefore, the sequence $\{\phi _n=x^Ne^{2\pi {i}nx}\}_{{\mathbb {Z}}\setminus \{0\}}$ is a GRS for $N=1$, see [15, p.158] and [28].

3.3 J-Orthonormal Sequences of the First/Second type

Let a sequence of real numbers $\{\alpha _{k}\}_{k=0}^{\infty }$ satisfy the conditions

$$\begin{aligned} 0\le \alpha _{0}<\alpha _{1}<\alpha _{2}\ldots , \qquad \lim _{k\rightarrow \infty }\alpha _k=\infty \end{aligned}$$

(3.4)

and let $\{{\mathsf {e}}_n\}_{n=0}^{\infty }$ be an ONB of ${\mathcal {H}}$ such that $J{\mathsf {e}}_n=(-1)^n{\mathsf {e}}_n$.

Each pair of orthonormal vectors $\{{\mathsf {e}}_{2k}, {\mathsf {e}}_{2k+1}\}_{k=0}^\infty$ can be identified with ${\mathbb {C}}^2$ assuming that

$$\begin{aligned} U{\mathsf {e}}_{2k}=\left[ \begin{array}{c} 1 \\ 0 \end{array}\right] , \qquad U{\mathsf {e}}_{2k+1}=\left[ \begin{array}{c} 0 \\ 1 \end{array}\right] . \end{aligned}$$

(3.5)

The operator U is an isometric mapping of the space ${\mathcal {H}}_k=\text{ span }\{{\mathsf {e}}_{2k}, {\mathsf {e}}_{2k+1}\}$ onto ${\mathbb {C}}^2$ and $UJ=\sigma _3{U}$, where $\sigma _3=\left[ \begin{array}{cc} 1 &{} 0 \\ 0 &{} -1 \end{array}\right]$. Since ${\mathcal {H}}=\sum _{k=0}^\infty \oplus {\mathcal {H}}_k$, the operator U can be extended to the isometric mapping of ${\mathcal {H}}$ onto the Hilbert space ${\mathbb {H}}$ of infinitely many copies of ${\mathbb {C}}^2$: ${\mathbb {H}}=\sum _{k=0}^\infty \oplus {\mathbb {C}}^2$. In the space ${\mathbb {H}}$, we define self-adjoint operators

$$\begin{aligned} {\mathbb {Q}}= & {} 2\sum _{k=0}^\infty \oplus \alpha _k\sigma _1, \quad e^{\mathbb {-Q}}=\sum _{k=0}^\infty \oplus {e^{-2\alpha _k\sigma _1}}, \nonumber \\ e^{{\mathbb {Q}}/2}= & {} \sum _{k=0}^\infty \oplus {e^{\alpha _k\sigma _1}}, \quad {\mathbb {J}}=\sum _{k=0}^\infty \oplus \sigma _3, \end{aligned}$$

(3.6)

where $\sigma _1=\left[ \begin{array}{cc} 0 &{}\quad 1 \\ 1 &{}\quad 0 \end{array}\right] .$ Theirs unitary equivalent copies in ${\mathcal {H}}$ are:

$$\begin{aligned} Q=U^{-1}{\mathbb {Q}}U, \quad e^{-Q}=U^{-1}e^{-{\mathbb {Q}}}U, \quad e^{Q/2}=U^{-1}e^{{\mathbb {Q}}/2}U, \quad J=U^{-1}{{\mathbb {J}}}U.\nonumber \\ \end{aligned}$$

(3.7)

By the construction, Q anticommutes with J: $JQ=-QJ$.

Consider vectors $\{\phi _n\}_{n=0}^\infty$ defined by the formulas:

$$\begin{aligned} \phi _{2k}= & {} \cosh \alpha _k{\mathsf {e}}_{2k}+\sinh \alpha _k{{\mathsf {e}}_{2k+1}}, \quad k=0,1,\dots \nonumber \\ \phi _{2k+1}= & {} \frac{c_k}{\sqrt{\mu _{2k+1}}}\sum _{n=0}^{\infty }\frac{\chi _n\cosh \alpha _n}{1-\mu _{2k+1}\cosh ^2\alpha _n}(\cosh \alpha _n{\mathsf {e}}_{2n+1}+\sinh \alpha _n{\mathsf {e}}_{2n}),\quad \end{aligned}$$

(3.8)

where $\{\chi _n\}_{n=0}^\infty$ is a vector from ${\ell _2({\mathbb {N}})}$ such that $\chi _n\not =0$; the set of numbers $0<\mu _{1}<\mu _{3}<\mu _{5}\ldots <1$ are roots of the equation

$$\begin{aligned} \sum _{n=0}^{\infty }\frac{|\chi _n\cosh \alpha _n|^2}{1-\mu \cosh ^2\alpha _n}=0 \end{aligned}$$

(3.9)

and

$$\begin{aligned} c_k=\left( {\sum _{n=0}^{\infty }\frac{|\chi _n|^2\cosh ^4\alpha _n}{(1-\mu _{2k+1}\cosh ^2\alpha _n)^2}}\right) ^{-\frac{1}{2}}, \quad k=0,1\ldots \end{aligned}$$

(3.10)

Theorem 3.2

Let the sequences $\{\alpha _{n}\}$ and $\{\chi _{n}\}$ satisfy the conditions above and let the sequence $\{\chi _n\cosh ^2\alpha _n\}$ do not belong to ${\ell _2({\mathbb {N}})}$. Then the vectors $\phi _n$ determined by (3.8) form a complete J-orthonormal sequence $\{\phi _n\}_{n=0}^\infty$ of the first type if $\{\chi _n\cosh \alpha _n\}\not \in {\ell _2({\mathbb {N}})}$ and of the second type if $\{\chi _n\cosh \alpha _n\}\in {\ell _2({\mathbb {N}})}$.

For the first type sequence $\{\phi _n\}$ the formula $\phi _n=e^{Q/2}e_n$ holds where Q and $e^{Q/2}$ are determined by (3.7) and an ONB $\{e_n\}$ has the form

$$\begin{aligned} e_{2k}={\mathsf {e}}_{2k}, \qquad e_{2k+1}= \frac{c_k}{\sqrt{\mu _{2k+1}}}\sum _{n=0}^{\infty }\frac{\chi _n\cosh \alpha _n}{1-\mu _{2k+1}\cosh ^2\alpha _n}{\mathsf {e}}_{2n+1}. \end{aligned}$$

(3.11)

For the second type sequence such a choice of Q and $\{e_n\}$ is impossible because the orthonormal system (3.11) is not dense in ${\mathcal {H}}$. A suitable operator Q can be chosen as $Q=-\ln {A_F}$, where $A_F$ is the Friedrichs extension of the symmetric operator S acting as $S\phi _n=(-1)^nJ\phi _n$ on vectors $\phi _n$ and extended onto ${\mathcal {D}}(S)=\text{ span }\{\phi _n\}$ by the linearity.

The proof of Theorem 3.2 is given in Sect. 4.

Let us consider a particular case assuming that

$$\begin{aligned} \tanh \alpha _n=\sqrt{\frac{n}{n+1}}, \qquad \chi _n=\frac{1}{(n+1)^{\frac{\delta +1}{2}}}, \quad n\ge {0}, \end{aligned}$$

and $0<\delta \le {2}$ (the condition $0<\delta$ guarantees that $\{\chi _n\}\in {\ell _2({\mathbb {N}})}$ while $\delta \le {2}$ ensures that $\{\chi _n\cosh ^2\alpha _n=1/(n+1)^{\delta /2-1/2}\}\not \in {\ell _2({\mathbb {N}})}$). Then the root Eq. (3.9) takes the form

$$\begin{aligned} \sum _{n=1}^{\infty }\frac{1}{n^\delta }\cdot \frac{1}{1-n\mu }=0, \end{aligned}$$

(3.12)

$c_k=\left( {\sum _{n=1}^{\infty }\frac{n^{1-\delta }}{(1-\mu _{2k+1}n)^2}}\right) ^{-\frac{1}{2}}$, and the sequence $\{\phi _n\}_{n=0}^\infty$:

$$\begin{aligned} \phi _{2k}= & {} \sqrt{k+1}{\mathsf {e}}_{2k}+\sqrt{k}{{\mathsf {e}}_{2k+1}}, \quad k=0, 1, 2\dots \\ \phi _{2k+1}= & {} \frac{c_k}{\sqrt{\mu _{2k+1}}}\sum _{n=1}^{\infty }\frac{1}{n^{\delta /2}}\cdot \frac{1}{1-n\mu _{2k+1}}(\sqrt{n}{\mathsf {e}}_{2n-1}+\sqrt{n-1}{\mathsf {e}}_{2n-2}), \end{aligned}$$

turns out to be the first kind if $0<\delta \le {1}$ and the second kind if $1<\delta \le {2}$.

Figure 1 contains a numerical localization of the first 5 roots of (3.12).

Fig. 1

First five roots to the Eq. (3.12) for different $\delta$ parameter value

Appendix: The Proof of Theorem 3.2

We refer [8, Subsection III.1] and [20] for results of the Krein space theory which are necessary for our exposition.

1.1 Preliminaries

An operator T defined by the formula

$$\begin{aligned} Te_{2k}=\tanh \alpha _k{\mathsf {e}}_{2k+1}, \qquad Te_{2k+1}=\tanh \alpha _k{\mathsf {e}}_{2k}, \qquad k=0,1,2\dots \end{aligned}$$

(4.1)

on the ONB $\{{\mathsf {e}}_n\}_{n=0}^\infty$ and extended onto ${\mathcal {H}}$ by the linearity is a self-adjoint strong contraction (‘strong’ means that $\Vert Tf\Vert <\Vert f\Vert$ for non-zero f). Moreover

$$\begin{aligned} JT=-TJ, \end{aligned}$$

(4.2)

since $J{\mathsf {e}}_n=(-1)^n{\mathsf {e}}_n$. The properties of T allow one to define J-orthogonal maximal positive ${\mathfrak {L}}_+$ and maximal negative ${\mathfrak {L}}_-$ subspaces of the Krein space $({\mathcal {H}}, [\cdot ,\cdot ])$ [20, Lemma 2.2]:

$$\begin{aligned} {\mathfrak {L}}_+=(I+T){\mathcal {H}}_+, \qquad {\mathfrak {L}}_-=(I+T){\mathcal {H}}_-, \end{aligned}$$

(4.3)

where ${\mathcal {H}}_+$ and ${\mathcal {H}}_-$ are the closure (in ${\mathcal {H}}$) of $\text{ span }\{{\mathsf {e}}_{2k}\}_{k=0}^\infty$ and $\text{ span }\{{\mathsf {e}}_{2k+1}\}_{k=0}^\infty$, respectively.

Consider a vector $\chi =\sum _{k=0}^\infty \chi _k{\mathsf {e}}_{2k+1}$, where $\{\chi _k\}$ belongs to ${\ell _2({\mathbb {N}})}$. By the construction, $\chi \in {\mathcal {H}}_{-}$ and

$$\begin{aligned} {\mathfrak {L}}_-^0=\{(I+T)g ,\ g\in M_- \}, \quad \text{ where } \quad M_-=\{g\in {\mathcal {H}}_-,\ (g, \chi )=0 \} \end{aligned}$$

(4.4)

is a subspace of the maximal negative space ${\mathfrak {L}}_-$ defined by (4.3).

The J-orthogonal sum ${\mathfrak {L}}_+{\dot{+}}{\mathfrak {L}}_-$ is dense in ${\mathcal {H}}$ since ${\mathfrak {L}}_\pm$ are maximal subspaces. However, we can not state that the set ${\mathfrak {L}}_+{\dot{+}}{\mathfrak {L}}_-^0$ remains dense in ${\mathcal {H}}$ since ${\mathfrak {L}}_-^0$ is a proper subspace of ${\mathfrak {L}}_-$.

Lemma 4.1

The sum ${\mathfrak {L}}_+{\dot{+}}{\mathfrak {L}}_-^0$ is dense in ${\mathcal {H}}$ if and only if $\left\{ \chi _n\cosh ^2\alpha _n\right\} \not \in \ell _2({\mathbb {N}})$.

Proof

Assume that $h\in {\mathcal {H}}$ is orthogonal to ${\mathfrak {L}}_+{\dot{+}}{\mathfrak {L}}_-^0$. Then Jh is orthogonal to ${\mathfrak {L}}_+$ with respect to the indefinite inner product $[\cdot ,\cdot ]$. Since ${\mathfrak {L}}_-$ is the J-orthogonal complement of ${\mathfrak {L}}_+$, the vector Jh belongs to ${\mathfrak {L}}_-$. By (4.3), $Jh=(I+T)f$, where $f\in {\mathcal {H}}_-$ and $h=J(I+T)f=(I-T)Jf=-(I-T)f.$

By the assumption, h is also orthogonal to ${\mathfrak {L}}_-^0$. In view of (4.4) this means that $0=(h, (I+T)g)=-((I-T)f, (I+T)g)=-((I-T^2)f, g)$ for all $g\in M_-$. Therefore, without loss of generality we can assume that $(I-T^2)f=\chi$. Here, $f=\sum _{k=0}^{\infty }{f_k {\mathsf {e}}_{2k+1}}$ since $f\in {\mathcal {H}}_-$. In view of (4.1),

$$\begin{aligned} (I-T^2)f=\sum _{k=0}^{\infty }{(1-\tanh ^2\alpha _k)f_k{\mathsf {e}}_{2k+1}} =\sum _{k=0}^{\infty }\frac{f_k}{\cosh ^2\alpha _k} {\mathsf {e}}_{2k+1}=\sum _{k=0}^{\infty }{\chi _k{\mathsf {e}}_{2k+1}}=\chi . \end{aligned}$$

Therefore, $f_k=\chi _k\cosh ^2\alpha _k$ and we arrive at the conclusion that ${\mathfrak {L}}_+\dot{+}{\mathfrak {L}}_-^0$ is a non-dense set in ${\mathcal {H}}$ if and only if $\{\chi _k\cosh ^2\alpha _k\}^\infty _{k=0}\in \ell _2({\mathbb {N}})$. $\square$

1.2 Complete J-Orthonormal Sequence $\{\phi _n\}$

Lemma 4.2

If $\{\chi _n\cosh ^2\alpha _n\}\not \in {\ell _2({\mathbb {N}})}$, then the vectors $\{\phi _n\}$ defined by (3.8) form a complete J-orthonormal sequence in ${\mathcal {H}}$.

Proof

The vectors $\{\phi _{2k}\}_{k=0}^\infty$ in (3.8) are J-orthonormal because [$\phi _{2k}, \phi _{2k'}]=0$ for $k\not =k'$ and $[\phi _{2k}, \phi _{2k}]=\cosh ^2\alpha _k-\sinh ^2\alpha _k=1.$ Moreover, in view of of (4.1), the vectors $\{\phi _{2k}\}$ can be presented as $\phi _{2k}=\cosh \alpha _k(I+T){\mathsf {e}}_{2k}$. This relation and (4.3) imply that the closure of $\text{ span }\{\phi _{2k}\}_{k=0}^{\infty }$ coincides with ${\mathfrak {L}}_+$.

By virtue of (4.1),

$$\begin{aligned} (I-T^2)f=\sum _{k=0}^{\infty }{(1-\tanh ^2\alpha _k)f_k{\mathsf {e}}_{2k+1}} \quad \text{ for } \text{ all } \quad f=\sum _{k=0}^{\infty }{f_k {\mathsf {e}}_{2k+1}}\in {\mathcal {H}}_-. \end{aligned}$$

This relation yields that $I-T^2$ is a compact operator in ${\mathcal {H}}_-$, since $\lim _{k\rightarrow \infty }(1-\tanh ^2\alpha _k)=0$, see [14, problem 132]. Therefore, $P_{M_-}(I-T^2)P_{M_-}$, where $P_{M_-}$ is an orthogonal projection in ${\mathcal {H}}_-$ onto the subspace $M_-$ defined in (4.4), is a self-adjoint compact operator in $M_-$. This implies the existence of an ONB $\{\gamma _{2k+1}\}$ of $M_-$ which is formed by eigenfunctions of $P_{M_-}(I-T^2)P_{M_-}$. Let $\{\mu _{2k+1}\}_{k=0}^\infty$ be the corresponding eigenvalues, i.e., $P_{M_-}(I-T^2)\gamma _{2k+1}=\mu _{2k+1}\gamma _{2k+1}$. Since $I-T^2$ is a positive contraction, we can state that $0<\mu _{2k+1}<{1}$ and $\lim _{k\rightarrow \infty }\mu _{2k+1}=0$.

Denote

$$\begin{aligned} \phi _{2k+1}=\frac{1}{\sqrt{\mu _{2k+1}}}(I+T)\gamma _{2k+1}, \qquad k=0,1\ldots \end{aligned}$$

(4.5)

The vectors $\{\phi _{2k+1}\}_{k=0}^\infty$ are J-orthonormal because

$$\begin{aligned} {[ \phi _{2k+1}, \phi _{2k'+1}]}= & {} -\frac{((I-T^2)\gamma _{2k+1}, \gamma _{2k'+1})}{\sqrt{\mu _{2k+1}\mu _{2k'+1}}} \nonumber \\= & {} -\sqrt{\frac{\mu _{2k+1}}{\mu _{2k'+1}}}(\gamma _{2k+1}, \gamma _{2k'+1})=-\delta _{kk'}. \end{aligned}$$

(4.6)

Moreover, in view of (4.4), $\phi _{2k+1}\in {{\mathfrak {L}}}_-^0$ and the closure of $\text{ span }\{\phi _{2k+1}\}_{k=0}^\infty$ coincides with ${{\mathfrak {L}}}_-^0$. Applying now Lemma 4.1 we arrive at the conclusion that, for the case $\{\chi _n\cosh ^2\alpha _n\}\not \in {\ell _2({\mathbb {N}})}$, the J-orthonormal sequence $\{\phi _n\}_{n=0}^\infty$, where $\{\phi _{2k}\}_{k=0}^\infty$ and $\{\phi _{2k+1}\}_{k=0}^\infty$ are defined by (3.8) and (4.5), respectively, is complete in ${\mathcal {H}}$.

To finish the proof of Lemma 4.2 it suffices to show that the formulas (3.8) and (4.5) determine the same vectors $\{\phi _{2k+1}\}_{k=0}^\infty$. To do that, we describe the eigenvalues $\mu _{2k+1}$ and the normalized eigenfunctions $\gamma _{2k+1}$ of the equation

$$\begin{aligned} P_{M_-}(I-T^2)g=\mu {g}, \qquad g\in {M_-}. \end{aligned}$$

(4.7)

In view of (4.4), the condition $g\in {M_-}$ means that

$$\begin{aligned} \sum _{k=0}^{\infty }g_k{\overline{\chi }}_k=0, \quad \text{ where } \quad g=\sum _{k=0}^{\infty }{g_k {\mathsf {e}}_{2k+1}}. \end{aligned}$$

(4.8)

Let $f=\sum _{k=0}^{\infty }{f_k {\mathsf {e}}_{2k+1}}$ be an arbitrary element of ${\mathcal {H}}_-$. Then

$$\begin{aligned} P_{M_-}f=\sum _{k=0}^{\infty }{(f_k-\alpha [f]\chi _k){\mathsf {e}}_{2k+1}}, \qquad \alpha [f]=\frac{1}{\Vert \chi \Vert ^2}\sum _{k=0}^{\infty }f_k{\overline{\chi }}_k. \end{aligned}$$

(4.9)

Using (4.9) we rewrite (4.7) as

$$\begin{aligned}&P_{M_-}\sum _{k=0}^{\infty }(1-\tanh ^2\alpha _k)g_k{\mathsf {e}}_{2k+1}\\&\qquad =\sum _{k=0}^{\infty }[(1-\tanh ^2\alpha _k)g_k-\alpha [(I-T^2)g]\chi _k]{\mathsf {e}}_{2k+1}=\mu \sum _{k=0}^{\infty }{g_k {\mathsf {e}}_{2k+1}} \end{aligned}$$

that implies

$$\begin{aligned} (1-\tanh ^2\alpha _k-\mu )g_k=\alpha [(I-T^2)g]\chi _k, \qquad k=0,1,\ldots \end{aligned}$$

(4.10)

It is important that $\alpha [(I-T^2)g]\not =0$ in (4.10). Indeed, if $\alpha [(I-T^2)g]=0$, then $(1-\tanh ^2\alpha _k-\mu )g_k=0$ for all k. Due to conditions imposed on $\alpha _n$ in (3.4), there exists a unique $k'$ such that $g_{k'}\not =0$ and $\mu =1-\tanh ^2\alpha _{k'}$. This means that $g=g_{k'}{\mathsf {e}}_{2k'+1}$ belongs to $M_-$. The last fact is impossible because $0=<g, \chi >=g_{k'}{\overline{\chi }}_{k'}\not =0$ (we recall that $\chi _n\not =0$ for all n by the assumption). The obtained contradiction shows that $\alpha [(I-T^2)g ]\not =0$. This means that $(1-\tanh ^2\alpha _k-\mu )g_k\not =0$ and (4.10) can be rewritten as

$$\begin{aligned} g_k=\alpha [(I-T^2)g]\frac{\chi _k\cosh ^2\alpha _k}{1-\mu \cosh ^2\alpha _k}, \qquad k=0,1,2\dots \end{aligned}$$

The corresponding solution $g(\mu )=\sum _{k=0}^{\infty }g_k{\mathsf {e}}_{2k+1}$ of (4.7) must be in $M_-$. By virtue of (4.8), $g(\mu )$ belongs to $M_-$ if and only if $\mu$ is the root of (3.9). The Eq. (3.9) has infinitely many roots $0<\mu _{1}<\mu _{3}<\ldots<\mu _{2k+1}\ldots <1$ that coincide with eigenvalues of $P_{M_-}(I-T^2)P_{M_-}$. The eigenfunctions of $P_{M_-}(I-T^2)P_{M_-}$ corresponding to $\mu _{2k+1}$ have the form

$$\begin{aligned} g(\mu _{2k+1})=\alpha [(I-T^2)g(\mu _{2k+1})]\sum _{n=0}^{\infty }\frac{\chi _n\cosh ^2\alpha _n}{1-\mu _{2k+1}\cosh ^2\alpha _n}{\mathsf {e}}_{2n+1}, \qquad k=0,1\ldots \end{aligned}$$

Then

$$\begin{aligned} \gamma _{2k+1}=\frac{g(\mu _{2k+1})}{\Vert g(\mu _{2k+1})\Vert }={c_k}\sum _{n=0}^{\infty }\frac{\chi _n\cosh ^2\alpha _n}{1-\mu _{2k+1}\cosh ^2\alpha _n}{\mathsf {e}}_{2n+1}, \qquad k=0,1\ldots , \end{aligned}$$

where the normalizing factor $c_k$ is defined in (3.10). By the construction, $\{\gamma _{2k+1}\}_{k=0}^\infty$ is an ONB of $M_-$. Substituting the obtained expression for $\gamma _{2k+1}$ into (4.5) and taking (4.1) into account, we obtain the vectors $\{\phi _{2k+1}\}$ from (3.8). $\square$

Lemma 4.3

If $\{\chi _n\cosh \alpha _n\}\not \in \ell _2({\mathbb {N}})$, then the sequence $\{\phi _n\}$ is of the first type. The corresponding operator Q in Definition 1.1 is defined by (3.7) while ONB $\{e_n\}$ has the form (3.11).

Proof

If $\{\chi _n\cosh \alpha _n\}\not \in {\ell _2({\mathbb {N}})}$, then $\{\chi _n\cosh ^2\alpha _n\}\not \in {\ell _2({\mathbb {N}})}$ and, by Lemma 4.2, $\{\phi _n\}$ is a complete J-orthonormal sequence. In view of (2.9), the operator S defined by (2.4) acts as $S\phi _n=(-1)^nJ\phi _n$. On the other hand, taking the relation $e^{-2\alpha _k\sigma _1}=\cosh {2\alpha _k}\sigma _0-\sinh {2\alpha _k}\sigma _1$ into account, we directly verify that $e^{-Q}\phi _n=(-1)^nJ\phi _n$, where $e^{-Q}$ is defined by (3.7). Therefore, $e^{-Q}$ is a positive self-adjoint extension of S. Denote $e_n=e^{-Q/2}\phi _n$. In view of (3.6),

$$\begin{aligned} e^{-Q/2}= & {} U^{-1}\sum _{k=0}^\infty \oplus [\cosh {\alpha _k}\sigma _0-\sinh {\alpha _k}\sigma _1]U\\= & {} U^{-1}\sum _{k=0}^\infty \oplus \left[ \begin{array}{cc} \cosh \alpha _k &{} -\sinh \alpha _k \\ -\sinh \alpha _k &{} \cosh \alpha _k \end{array}\right] U. \end{aligned}$$

This expression, (3.5), and (3.8) allow one to calculate $\{e_n\}$ precisely, as (3.11).

By analogy with the proof of Theorem  2.5 we obtain that $\{e_n\}$ is an orthonormal sequence in ${\mathcal {H}}$. Moreover, $\{e_n\}$ is an ONB if and only if $\{\phi _n\}$ is complete in the Hilbert space ${\mathcal {H}}_{-Q}$. Below we show that the completeness of $\{\phi _n\}$ in ${\mathcal {H}}_{-Q}$ is equivalent to the condition $\{\chi _n\cosh \alpha _n\}\not \in \ell _2({\mathbb {N}})$.

We begin with the remark that

$$\begin{aligned} e^{-Q}=(I-T)(I+T)^{-1}, \end{aligned}$$

(4.11)

where T is determined by (4.1).

Indeed, since the subspaces ${\mathcal {H}}_k=\text{ span }\{{\mathsf {e}}_{2k}, {\mathsf {e}}_{2k+1}\}$ are invariant with respect to T and U satisfies (3.5), we get that $UTU^{-1}|_{{\mathcal {H}}_k}$ acts as the multiplication by $\tanh \alpha _k\sigma _1$ in ${\mathbb {C}}^2$ and $U(I-T)(I+T)^{-1}U^{-1}|_{{\mathcal {H}}_k}$ coincides with

$$\begin{aligned} \left[ \begin{array}{cc} \cosh \alpha _k &{} -\sinh \alpha _k \\ -\sinh \alpha _k &{} \cosh \alpha _k \end{array}\right] ^2= & {} \left[ \begin{array}{cc} \cosh 2\alpha _k &{} -\sinh 2\alpha _k \\ -\sinh 2\alpha _k &{} \cosh 2\alpha _k \end{array}\right] \\= & {} (\cosh 2\alpha _k\sigma _0-\sinh 2\alpha _k\sigma _1)^2=e^{-2\alpha _k\sigma _1}. \end{aligned}$$

This relation and the decomposition ${\mathcal {H}}=\sum _{k=0}^\infty \oplus {\mathcal {H}}_k$ justify (4.11).

The formulas (4.3) and (4.11) lead to the conclusion that ${\mathcal {D}}(e^{-Q})={\mathfrak {L}}_+{\dot{+}}{\mathfrak {L}}_-$, where the subspaces ${\mathfrak {L}}_\pm$ are orthogonal with respect to the inner product (2.3). Therefore, the space ${\mathcal {H}}_{-Q}$ has the decomposition

$$\begin{aligned} {\mathcal {H}}_{-Q}=\widehat{{\mathfrak {L}}}_+{\dot{+}}\widehat{{\mathfrak {L}}}_- \end{aligned}$$

where the subspaces $\widehat{{\mathfrak {L}}}_\pm$ are the completions of linear manifolds ${{\mathfrak {L}}}_\pm$ in ${\mathcal {H}}_{-Q}$.

To prove the completeness of $\{\phi _n\}$ in ${\mathcal {H}}_{-Q}$ we note that $\{\phi _{2k}\}$ is a complete set in $\widehat{{{\mathfrak {L}}}}_+$. This fact can be justified as follows: due to the proof of Lemma 4.2, $\text{ span }\{\phi _{2k}\}$ is dense in the subspace ${\mathfrak {L}}_+$ of ${\mathcal {H}}$. In view of (4.2), (4.3), and (4.11),

$$\begin{aligned} \Vert f\Vert _{-Q}^2=(e^{-Q}f,f)=((I-T)x_+, (I+T)x_+)=[f,f]\le \Vert f\Vert ^2 \end{aligned}$$

for each $f=(I+T)x_+\in {\mathfrak {L}}_+$. Therefore, each $f\in {\mathfrak {L}}_+$ can be approximated by vectors from $\text{ span }\{\phi _{2k}\}$ with respect to the norm $\Vert \cdot \Vert _{-Q}$. Since $\widehat{{{\mathfrak {L}}}}_+$ is the completion of ${\mathfrak {L}}_+$ in ${\mathcal {H}}_{-Q}$, the set $\{\phi _{2k}\}$ is complete in $\widehat{{{\mathfrak {L}}}}_+$.

Similar arguments and the fact that $\text{ span }\{\phi _{2k+1}\}$ is dense in the subspace ${\mathfrak {L}}_-^0$ lead to the conclusion that each vector $f\in {\mathfrak {L}}_-^0$ can be approximated by vectors of $\text{ span }\{\phi _{2k+1}\}$ with respect to $\Vert \cdot \Vert _{-Q}$. Therefore, in order to proof the completeness of $\{\phi _{2k+1}\}$ in $\widehat{{{\mathfrak {L}}}}_-$ it suffices to find when ${\mathfrak {L}}_-^0$ turns out to be dense in $\widehat{{{\mathfrak {L}}}}_-$ with respect to $\Vert \cdot \Vert _{-Q}$.

Let $h\in \widehat{{{\mathfrak {L}}}}_-$ be orthogonal to ${\mathfrak {L}}_-^0$ in ${\mathcal {H}}_{-Q}$. Since ${\mathfrak {L}}_-$ is dense in $\widehat{{{\mathfrak {L}}}}_-$ we can approximate h by a sequence $\{f_n\}$, where $f_n\in {\mathfrak {L}}_-$. In view of (2.3), the sequence $\{e^{-Q/2}f_n\}$ is fundamental in ${\mathcal {H}}$ and, hence, $\lim _{n\rightarrow \infty }e^{-Q/2}f_n=f\in {\mathcal {H}}$. Due to (4.3), $f_n=(I+T)x_{-}^n$, where $x_-^n\in {\mathcal {H}}_-$. Moreover, $e^{-Q/2}=[(I-T)(I+T)^{-1}]^{1/2}$ in view of (4.11). This means that

$$\begin{aligned} e^{-Q/2}f_n=[(I-T)(I+T)^{-1}]^{1/2}(I+T)x_{-}^n=(I-T^2)^{1/2}x_-^n \end{aligned}$$

and, since $(I-T^2)^{1/2}$ leaves ${\mathcal {H}}_\pm$ invariant, $f=\lim _{n\rightarrow \infty }e^{-Q/2}f_n=\lim _{n\rightarrow \infty }(I-T^2)^{1/2}x_-^n=f\in {\mathcal {H}}_-$. On the other hand, for each vector $(I+T)g\in {\mathfrak {L}}_-^0$, the relation $e^{-Q/2}(I+T)g=(I-T^2)^{1/2}g$ holds. After such kind of auxiliary work we obtain:

$$\begin{aligned} 0= & {} (h, (I+T)g)_{-Q}=\lim _{n\rightarrow \infty }(f_n, (I+T)g)_{-Q}= \lim _{n\rightarrow \infty }(e^{-Q/2}f_n, e^{-Q/2}(I+T)g)\\= & {} (f, (I-T^2)^{1/2}g)=((I-T^2)^{1/2}f, g) \quad \text{ for } \text{ all } \quad g\in M_-. \end{aligned}$$

Therefore, without loss of generality we can assume that $(I-T^2)^{1/2}f=\chi$. Reasoning by analogy with the final part of the proof of Lemma 4.1, we obtain that ${\mathfrak {L}}_-^0$ is dense in $\widehat{{{\mathfrak {L}}}}_-$ if and only if $\{\chi _n\cosh \alpha _n\}\not \in \ell _2({\mathbb {N}})$. This relation guarantees the completeness of $\{\phi _n\}$ in ${\mathcal {H}}_{-Q}$. $\square$

1.3 The Proof of Theorem 3.2

The implication $`\{\chi _n\cosh \alpha _n\}\not \in {\ell _2({\mathbb {N}})} \rightarrow \{\phi _n\}$ is a first type sequence’ was proved in Lemma 4.3. Let us assume that $\{\phi _n\}$ is of the first type, i.e., there exists a self-adjoint operator $Q'$ anti-commuting with J and such that $\phi _n=e^{Q'/2}e_n'$, where $\{e_n'\}$ is an ONB of ${\mathcal {H}}$.

Denote ${\mathcal {C}}=Je^{-Q'}$. Since $Q'$ anti-commutes with J, the operator ${\mathcal {C}}$ satisfies the relation ${\mathcal {C}}^2f=f$ for $f\in {\mathcal {D}}({\mathcal {C}})$ and $J{\mathcal {C}}=e^{-Q'}$ is a positive self-adjoint operator in ${\mathcal {H}}$. In view of [7, Theorem 6.2.3], there exists J-orthonormal maximal positive ${\mathfrak {L}}_+'$ and maximal negative ${\mathfrak {L}}_-'$ subspaces of the Krein space $({\mathcal {H}}, [\cdot ,\cdot ])$ which uniquely characterize ${\mathcal {C}}$ in the following way: ${\mathcal {C}}{f_+}=f_+$ and ${\mathcal {C}}{f_-}=f_-$ for $f_\pm \in {\mathfrak {L}}_\pm '$.

Since $e^{-Q'}$ is an extension of S, we obtain ${\mathcal {C}}\phi _n=Je^{-Q'}\phi _n=JS\phi _n=(-1)^{n}\phi _n$. Therefore, the operator ${\mathcal {C}}$ acts as the identity operator on elements of the subspace ${\mathfrak {L}}_+$ defined by (4.3) (since $\text{ span }\{\phi _{2k}\}_{k=0}^{\infty }$ is dense in ${\mathfrak {L}}_+$). This yields that ${\mathfrak {L}}_+'={\mathfrak {L}}_+$ and, moreover ${\mathfrak {L}}_-'={\mathfrak {L}}_-$ since the maximal negative subspace ${\mathfrak {L}}_-'$ is determined uniquelly as J-orthogonal complement of ${\mathfrak {L}}_+'={\mathfrak {L}}_+$. We obtain that the J-orthogonal sum ${\mathfrak {L}}_+\dot{+}{\mathfrak {L}}_-$ determines two operators $Je^{-Q'}$ and $Je^{-Q}$. Applying again [7, Theorem 6.2.3], we conclude that $Q'=Q$, where Q is determined by (3.7). In this case, $e_n'=e^{-Q'/2}\phi _n=e^{-Q/2}\phi _n=e_n$, where $\{e_n\}$ is determined by (3.11). Therefore, $\{e_n\}$ is an ONB of ${\mathcal {H}}$ that, in view of the proof of Lemma 4.3 is equivalent to the condition $\{\chi _n\cosh \alpha _n\}\not \in {\ell _2({\mathbb {N}})}$. The inverse implication ‘first type sequence $\{\phi _n\} \rightarrow \{\chi _n\cosh \alpha _n\}\not \in {\ell _2({\mathbb {N}})}$ ’ is proved.

If $\{\phi _n\}$ is second type, the choice of Q as in (3.7) leads to the non-complete orthonormal sequence (3.11) in ${\mathcal {H}}$. Trying to keep the GRS’s formula $\phi _n=e^{Q/2}e_n$ we have to use $Q=-\ln A$, where A is a positive extremal extension of S (without loss of generality, we may assume that $A=A_F$). In this case, the ONB $\{e_n\}$ will be different from (3.11).