Skip to main content
SpringerLink
Log in

Performance analysis of high-static-low-dynamic stiffness vibration isolator with time-delayed displacement feedback

  • Published:
Journal of Central South University Aims and scope Submit manuscript

Abstract

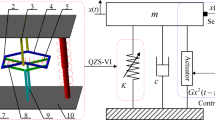
The displacement feedback with time delay considered is introduced in order to enhance the vibration isolation performance of a high-static-low-dynamic stiffness (HSLDS) vibration isolator. Such feedback is detailedly analyzed from the viewpoint of equivalent damping. Firstly, the primary resonance of the controlled HSLDS vibration isolator subjected to a harmonic force excitation is obtained based on the multiple scales method and further verified by numerical integration. The stability of the primary resonance is subsequently investigated. Then, the equivalent damping is defined to study the effects of feedback gain and time delay on primary resonance. The condition of jump avoidance is obtained with the purpose of eliminating the adverse effects induced by jumps. Finally, the force transmissibility of the controlled HSLDS vibration isolator is defined to evaluate its isolation performance. It is shown that an appropriate choice of feedback parameters can effectively suppress the force transmissibility in resonant region and reduce the resonance frequency. Furthermore, a wider vibration isolation frequency bandwidth can be achieved compared to the passive HSLDS vibration isolator.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. IBRAHIM R A. Recent advances in nonlinear passive vibration isolators [J]. Journal of Sound and Vibration, 2008, 314(3): 371-452.

    Article  Google Scholar 

  2. PLATUS D L. Negative-stiffness-mechanism vibration isolation systems [C]// Proceedings of SPIE-The International Society for Optical Engineering. Denver: International Society for Optical Engineering, 1999: 98-105.

    Google Scholar 

  3. CARRELLA A, BRENNAN M J, WATERS T P. Static analysis of a passive vibration isolation with quasi zero-stiffness characteristic [J]. Journal of Sound and Vibration, 2007, 301(3): 678-689.

    Article  Google Scholar 

  4. CARRELLA A, BRENNAN M J, WATERS T P, LOPES J V. Force and displacement transmissibility of a nonlinear isolator with high-static-low-dynamic-stiffness [J]. International Journal of Mechanical Sciences, 2012, 55(1): 22-29.

    Article  Google Scholar 

  5. ROBERTSON W S, KIDNER M R F, CAZZOLATO B S, ZANDER A C. Theoretical design parameters for a quasi-zero stiffness magnetic spring for vibration isolation [J]. Journal of Sound and Vibration, 2009, 326(1, 2): 88-103.

    Article  Google Scholar 

  6. ZHOU N, LIU K. A tunable high-static low-dynamic stiffness vibration isolator [J]. Journal of Sound and Vibration, 2010, 329(9): 1254-1273.

    Article  Google Scholar 

  7. XU D L, YU Q P, ZHOU J X, BISHOP S R. Theoretical and experimental analyses of a nonlinear magnetic vibration isolator with quasi-zero-stiffness characteristic [J]. Journal of Sound and Vibration, 2013, 332(14): 3377-3389.

    Article  Google Scholar 

  8. LIU X T, HUANG X C, HUA H X. On the characteristics of a quasi-zero stiffness isolator using Euler buckled beam as negative stiffness corrector [J]. Journal of Sound and Vibration, 2013, 332(14): 3359-3376.

    Article  Google Scholar 

  9. HUANG X C, LIU X T, SUN J Y, ZHANG Z Y, HUA H X. Effect of the system imperfections on the dynamic response of a high-static-low-dynamic stiffness vibration isolator [J]. Nonlinear Dynamics, 2014, 76(2): 1157-1167.

    Article  MathSciNet  Google Scholar 

  10. SHAW A D, NEILD S A, WAGG D J, WEAVER P M, CARRELLA A. A nonlinear spring mechanism incorporating a bistable composite plate for vibration isolation [J]. Journal of Sound and Vibration, 2013, 332(24): 6265-6275.

    Article  Google Scholar 

  11. ZHOU J X, WANG X L, XU D L, BISHOP S R. Nonlinear dynamic characteristics of a quasi-zero stiffness vibration isolator with cam-roller-spring mechanisms [J]. Journal of Sound and Vibration, 2015, 346: 53-69.

    Article  Google Scholar 

  12. CHENG C, LI S M, WANG Y, JIANG X X. On the analysis of a piecewise nonlinear-linear vibration isolator with high-static-lowdynamic- stiffness under base excitation [J]. Journal of Vibroengineering, 2015, 17(7): 3453-3470.

    Google Scholar 

  13. HU H Y, DOWELL E H, VIRGIN L N. Resonances of a harmonically forced Duffing oscillator with time delay state feedback [J]. Nonlinear Dynamics, 1998, 15(4): 311-327.

    Article  MATH  Google Scholar 

  14. ELLIOTT S J, SERRAND M, GARDONIO P. Feedback stability limits for active isolation system with reactive and inertial actuators [J]. Journal of Vibration and Acoustics, 2001, 123(2): 250-261.

    Article  Google Scholar 

  15. LIU Y, WATERS T P, BRENNAN M J. A comparison of semi-active damping control strategies for vibration isolation of harmonic disturbances [J]. Journal of Sound and Vibration, 2005, 280(1, 2): 21-39.

    Article  MathSciNet  MATH  Google Scholar 

  16. LI K A, XIAO H, CUI R F. Bifurcation control of nonlinear oscillator in primary and secondary resonance [J]. Journal of Central South University, 2007, 14(6): 826-831.

    Article  Google Scholar 

  17. GAO X, CHEN Q. Nonlinear analysis, design and vibration isolation for a bilinear system with time-delayed cubic velocity feedback [J]. Journal of Sound and Vibration, 2014, 333(6): 1562-1576.

    Article  Google Scholar 

  18. HUANG D M, XU W, XIE W X, HAN Q. Principle resonance response of a stochastic elastic impact oscillator under nonlinear delayed state feedback [J]. Chinese Physics B, 2015, 24(4): 040502.

    Article  Google Scholar 

  19. WANG Y, LI S M, CHENG C, JIANG X X. Dynamic analysis of a high-static-low-dynamic-stiffness vibration isolator with timedelayed feedback control [J]. Shock and Vibration, 2015, 2015: 1-19.

    Google Scholar 

  20. SUN X T, XU J, JIN X J, CHENG L. Beneficial performance of a quasi-zero-stiffness vibration isolator with time-delayed active control [J]. International Journal of Mechanical Sciences, 2014, 82: 32-40.

    Article  Google Scholar 

  21. SCHMIDT G, TONDL A. Non-Linear Vibrations [M]. Cambridge: Cambridge University Press, 1986.

    Book  MATH  Google Scholar 

  22. JAZAR G N, HOUIM R, NARIMANI A, GOLNARAGHI M F. Frequency response and jump avoidance in a nonlinear passive engine mount [J]. Journal of Vibration and Control, 2006, 12(11): 1205-1237.

    Article  MATH  Google Scholar 

  23. JAZAR G N, MAHINFALAH M, DESHPANDE S. Design of a piecewise linear vibration isolator for jump avoidance [J]. Proceedings of the Institution of Mechanical Engineers, Part K: Journal of Multi-body Dynamics, 2007, 221(3): 441-449.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. College of Energy and Power Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing, 210016, China

    Chun Cheng  (程春), Shun-ming Li  (李舜酩), Yong Wang  (王勇) & Xing-xing Jiang  (江星星)

Authors
  1. Chun Cheng  (程春)
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Shun-ming Li  (李舜酩)
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Yong Wang  (王勇)
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Xing-xing Jiang  (江星星)
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Shun-ming Li  (李舜酩).

Additional information

Foundation item: Project(KYLX15_0256) supported by the Funding of Jiangsu Innovation Program for Graduate Education, China; Project(SV2015-KF-01) supported by the Open Project of State Key Laboratory for Strength and Vibration of Mechanical Structures, China; Project(XZA15003) supported by the Fundamental Research Funds for the Central Universities, China

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Cheng, C., Li, Sm., Wang, Y. et al. Performance analysis of high-static-low-dynamic stiffness vibration isolator with time-delayed displacement feedback. J. Cent. South Univ. 24, 2294–2305 (2017). https://doi.org/10.1007/s11771-017-3641-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11771-017-3641-3

Key words

Search

Navigation