Skip to main content
SpringerLink
Log in

A branch-price-and-cut algorithm for the vehicle routing problem with time windows and multiple deliverymen

  • Original Paper
  • Published:
TOP Aims and scope Submit manuscript

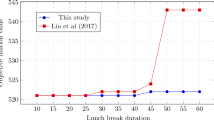
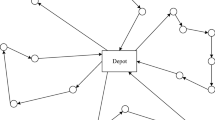
Abstract

We address a variant of the vehicle routing problem with time windows that includes the decision of how many deliverymen should be assigned to each vehicle. In this variant, the service time at each customer depends on the size of the respective demand and on the number of deliverymen assigned to visit this customer. In addition, the objective function consists of minimizing a weighted sum of the total number of routes, number of deliverymen and traveled distance. These characteristics make this variant very challenging for exact methods. To date, only heuristic approaches have been proposed for this problem, and even the most efficient optimization solvers cannot find optimal solutions in a reasonable amount of time for instances of moderate size when using the available mathematical formulations. We propose a branch-price-and-cut method based on a new set partitioning formulation of the problem. To accelerate the convergence of the method, we rely on an interior-point column and cut generation process, a strong branching strategy and a mixed-integer programming-based primal heuristic. Additionally, a hierarchical branching strategy is used to take into account the different components of the objective function. The computational results indicate the benefits of using the proposed exact solution approach. We closed several instances of the problem and obtained upper bounds that were previously unknown in the literature.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Achterberg T, Koch T, Martin A (2005) Branching rules revisited. Oper Res Lett 33(1):42–54

    Article  Google Scholar 

  • Álvarez A, Munari P (2016) Metaheuristic approaches for the vehicle routing problem with time windows and multiple deliverymen. Gest Prod 23(2):279–293

    Article  Google Scholar 

  • Archetti C, Speranza MG (2014) A survey on matheuristics for routing problems. EURO J Comput Optim 2(4):223–246

    Article  Google Scholar 

  • Baldacci R, Mingozzi A, Roberti R (2012) Recent exact algorithms for solving the vehicle routing problem under capacity and time window constraints. Eur J Oper Res 218(1):1–6

    Article  Google Scholar 

  • Bard JF, Kontoravdis G, Yu G (2002) A branch-and-cut procedure for the vehicle routing problem with time windows. Transp Sci 36(2):250–269

    Article  Google Scholar 

  • Ben Amor HM, Desrosiers J, Frangioni A (2009) On the choice of explicit stabilizing terms in column generation. Discrete Appl Math 157(6):1167–1184

    Article  Google Scholar 

  • Berbeglia G, Cordeau J-F, Gribkovskaia I, Laporte G (2007) Static pickup and delivery problems: a classification scheme and survey. Top 15(1):1–31

    Article  Google Scholar 

  • Briant O, Lemarechal C, Meurdesoif P, Michel S, Perrot N, Vanderbeck F (2008) Comparison of bundle and classical column generation. Math Program 113(2):299–344

    Article  Google Scholar 

  • Ceselli A, Righini G, Tresoldi E (2014) Vehicle routing problems with different service constraints: a branch-and-cut-and-price algorithm. Networks 64(4):282–291

    Article  Google Scholar 

  • Chabrier A (2006) Vehicle routing problem with elementary shortest path based column generation. Comput Oper Res 33(10):2972–2990

    Article  Google Scholar 

  • Contardo C, Desaulniers G, Lessard F (2015) Reaching the elementary lower bound in the vehicle routing problem with time windows. Networks 65(1):88–99

    Article  Google Scholar 

  • Desaulniers G, Lessard F, Hadjar A (2008) Tabu search, partial elementarity, and generalized k-path inequalities for the vehicle routing problem with time windows. Transp Sci 42(3):387–404

    Article  Google Scholar 

  • Desaulniers G, Madsen OB, Ropke S (2014) The vehicle routing problem with time windows. In: Vehicle routing: problems, methods, and applications. Society for industrial and applied mathematics, chap 5, 2nd edn, pp 119–159

    Chapter  Google Scholar 

  • Desrosiers J, Lübbecke ME (2011) Branch-price-and-cutalgorithms. In: Cochran JJ, Cox LA, Keskinocak P, Kharoufeh JP, Smith JC (eds) Wiley encyclopedia of operations research and management science. Wiley, Berlin

    Google Scholar 

  • Elhedhli S, Goffin J-L (2004) The integration of an interior-point cutting plane method within a branch-and-price algorithm. Math Program 100:267–294

    Article  Google Scholar 

  • Feillet D, Dejax P, Gendreau M, Gueguen C (2004) An exact algorithm for the elementary shortest path problem with resource constraints: application to some vehicle routing problems. Networks 44:216–229

    Article  Google Scholar 

  • Ferreira VO, Pureza V (2012) Some experiments with a savings heuristic and a tabu search approach for the vehicle routing problem with multiple deliverymen. Pesqui Oper 32:443–463

    Article  Google Scholar 

  • Ford LR, Fulkerson DR (1958) A suggested computation for maximal multi-commodity network flows. Manag Sci 5(1):97–101

    Article  Google Scholar 

  • Frangioni A (2002) Generalized bundle methods. SIAM J Optim 13:117–156

    Article  Google Scholar 

  • Fukasawa R, Longo H, Lysgaard J, de Aragão MP, Reis M, Uchoa E, Werneck RF (2006) Robust branch-and-cut-and-price for the capacitated vehicle routing problem. Math Program 106(3):491–511

    Article  Google Scholar 

  • Goffin JL, Vial JP (2002) Convex nondifferentiable optimization: a survey focussed on the analytic center cutting plane method. Optim Methods Softw 17(5):805–867

    Article  Google Scholar 

  • Golden BL, Raghavan S, Wasil EA (2008) The vehicle routing problem: latest advances and new challenges, vol 43. Springer, Berlin

    Book  Google Scholar 

  • Gondzio J (2012) Interior point methods 25 years later. Eur J Oper Res 218(3):587–601

    Article  Google Scholar 

  • Gondzio J, Gonzalez-Brevis P, Munari P (2013) New developments in the primal-dual column generation technique. Eur J Oper Res 224(1):41–51

    Article  Google Scholar 

  • Gondzio J, González-Brevis P, Munari P (2016) Large-scale optimization with the primal-dual column generation method. Math Program Comput 8(1):47–82

    Article  Google Scholar 

  • Iori M, Martello S (2010) Routing problems with loading constraints. Top 18(1):4–27

    Article  Google Scholar 

  • Irnich S, Desaulniers G (2005) Shortest path problems with resource constraints. In: Desaulniers G, Desrosiers J, Solomon MM (eds) Column generation. Springer, New York, pp 33–65

    Chapter  Google Scholar 

  • Jepsen M, Petersen B, Spoorendonk S, Pisinger D (2008) Subset-row inequalities applied to the vehicle routing problem with time windows. Oper Res 56(2):497–511

    Article  Google Scholar 

  • Klabjan D, Johnson E, Nemhauser G, Gelman E, Ramaswamy S (2001) Solving large airline crew scheduling problems: random pairing generation and strong branching. Comput Optim Appl 20(1):73–91

    Article  Google Scholar 

  • Linderoth JT, Savelsbergh MW (1999) A computational study of search strategies for mixed integer programming. INFORMS J Comput 11(2):173–187

    Article  Google Scholar 

  • Lübbecke ME, Desrosiers J (2005) Selected topics in column generation. Oper Res 53(6):1007–1023

    Article  Google Scholar 

  • Munari P, Gondzio J (2013) Using the primal-dual interior point algorithm within the branch-price-and-cut method. Comput Oper Res 40(8):2026–2036

    Article  Google Scholar 

  • Munari P, Gondzio J (2015) Column generation and branch-and-price with interior point methods. In: Proceeding series of the Brazilian society of computational and applied mathematics, vol 3, no. 1. https://doi.org/10.5540/03.2015.003.01.0525

  • Pecin D, Contardo C, Desaulniers G, Uchoa E (2017a) New enhancements for the exact solution of the vehicle routing problem with time windows. INF J Comput 29(3):489–502

    Article  Google Scholar 

  • Pecin D, Pessoa A, Poggi M, Uchoa E (2017b) Improved branch-cut-and-price for capacitated vehicle routing. Math Program Comput 9(1):61–100

    Article  Google Scholar 

  • Pessoa A, Sadykov R, Uchoa E, Vanderbeck F (2013) In-out separation and column generation stabilization by dual price smoothing. In: International symposium on experimental algorithms. Springer, pp 354–365

  • Pureza V, Morabito R, Reimann M (2012) Vehicle routing with multiple deliverymen: modeling and heuristic approaches for the VRPTW. Eur J Oper Res 218(3):636–647

    Article  Google Scholar 

  • Ralphs T, Kopman L, Pulleyblank WR, Trotter LE (2003) On the capacitated vehicle routing problem. Math Program 94(2–3):343–359

    Article  Google Scholar 

  • Righini G, Salani M (2008) New dynamic programming algorithms for the resource constrained elementary shortest path problem. Networks 51(3):155–170

    Article  Google Scholar 

  • Ropke S, Cordeau J-F (2009) Branch and cut and price for the pickup and delivery problem with time windows. Transp Sci 43(3):267–286

    Article  Google Scholar 

  • Rousseau L-M, Gendreau M, Feillet D (2007) Interior point stabilization for column generation. Oper Res Lett 35(5):660–668

    Article  Google Scholar 

  • Santos LM, Munari P, Costa AM, Santos RH (2015) A branch-price-and-cut method for the vegetable crop rotation scheduling problem with minimal plot sizes. Eur J Oper Res 245(2):581–590

    Article  Google Scholar 

  • Senarclens de Grancy G, Reimann M (2014) Vehicle routing problems with time windows and multiple service workers: a systematic comparison between ACO and GRASP. Cent Eur J Oper Res 23:1–20

    Google Scholar 

  • Senarclens de Grancy G, Reimann M (2015) Evaluating two new heuristics for constructing customer clusters in a VRPTW with multiple service workers. Cent Eur J Oper Res 23:479–500

    Article  Google Scholar 

  • Solomon MM (1987) Algorithms for the vehicle routing and scheduling problems with time window constraints. Oper Res 35(2):254–265

    Article  Google Scholar 

  • Spliet R, Desaulniers G (2015) The discrete time window assignment vehicle routing problem. Eur J Oper Res 244(2):379–391

    Article  Google Scholar 

  • Subramanian A, Uchoa E, Ochi LS (2013) A hybrid algorithm for a class of vehicle routing problems. Comput Oper Res 40(10):2519–2531

    Article  Google Scholar 

  • Toth P, Vigo D (eds) (2014) Vehicle routing: problems, methods and applications. MOS-SIAM series in optimization, 2nd edn. https://doi.org/10.1137/1.9781611973594

    Google Scholar 

  • Vanderbeck F (2005) Implementing mixed integer column generation. In: Desaulniers G, Desrosiers J, Solomon MM (eds) Column generation. Springer, New York, pp 331–358

    Chapter  Google Scholar 

  • Wentges P (1997) Weighted Dantzig–Wolfe decomposition for linear mixed-integer programming. Int Trans Oper Res 4(2):151–162

    Google Scholar 

Download references

Acknowledgements

We would like to thank the two anonymous referees, who have made valuable comments and certainly improved the content of this paper.

Author information

Authors and Affiliations

  1. Production Engineering Department, Federal University of Sao Carlos, Rodovia Washington Luis Km 235, Sao Carlos, SP, Brazil

    Pedro Munari & Reinaldo Morabito

Authors
  1. Pedro Munari
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Reinaldo Morabito
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Pedro Munari.

Additional information

This research has been supported by FAPESP (Sao Paulo Research Foundation, Brazil) under project numbers 2014/00939-8 and 2016/01860-1 and CNPq (Conselho Nacional de Desenvolvimento Cientifico e Tecnologico, Brazil) under project numbers 482664/2013-4 and 479328/2013-7.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Munari, P., Morabito, R. A branch-price-and-cut algorithm for the vehicle routing problem with time windows and multiple deliverymen. TOP 26, 437–464 (2018). https://doi.org/10.1007/s11750-018-0481-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11750-018-0481-8

Keywords

Mathematics Subject Classification

Search

Navigation