Abstract
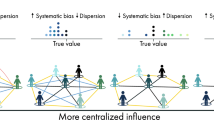
We propose an agent-based model of collective opinion formation to study the wisdom of crowds under social influence. The opinion of an agent is a continuous positive value, denoting its subjective answer to a factual question. The wisdom of crowds states that the average of all opinions is close to the truth, i.e., the correct answer. But if agents have the chance to adjust their opinion in response to the opinions of others, this effect can be destroyed. Our model investigates this scenario by evaluating two competing effects: (1) agents tend to keep their own opinion (individual conviction), (2) they tend to adjust their opinion if they have information about the opinions of others (social influence). For the latter, two different regimes (full information vs. aggregated information) are compared. Our simulations show that social influence only in rare cases enhances the wisdom of crowds. Most often, we find that agents converge to a collective opinion that is even farther away from the true answer. Therefore, under social influence the wisdom of crowds can be systematically wrong.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Problems of collective decisions are tackled in different scientific disciplines, from biology to sociology, from computer science to management science, from robotics to statistical physics. But the overarching research interest is the same: Collective decision processes should, in the best case, ensure an unanimous outcome, often denoted as consensus (Bose et al. 2017). Taking a social perspective, individuals likely have deviating opinions regarding a particular issue. But thanks to social interactions during the process of collective opinion formation, individuals are able to adapt their opinions such that eventually a majority converges to the same opinion. This ideal picture is distorted in reality in several ways. To put forward the problem addressed in this paper: converging to the same opinion does not imply converging to the right opinion. Collective decision processes can easily converge to a consensus that is wrong in an objective sense, because of social influence among individuals.
The term social influence encompasses several aspects that are underestimated, or not yet understood regarding their consequences for opinion dynamics (Flache et al. 2017). For example, what is the role of social pressure, external influences, or affective involvement in collective decisions? Of particular importance is the question how individuals respond to the information they obtain about the opinions of others. This question will be further addressed in our paper. For a systematic investigation, we utilize agent-based models that allow to vary such responses and to study their impact on the collective opinion.
Many agent-based models of opinion dynamics use a binary characterization of opinions, e.g., \(\{0,1\}\) or \(\{-1,+1\}\). A particular class of stochastic models, the so-called “voter models” (Dornic et al. 2001; Castellano et al. 2009), study how agents respond to the frequencies of these opinions in a predefined neighborhood (Banisch 2014; Fernández-Gracia et al. 2014). In the linear voter model, the majority rule assumes that the opinion of the (local) majority is adopted with a probability directly proportional to the frequency of a given opinion. It can be shown analytically that such assumptions usually result in consensus. The question thus is how long it takes before this outcome is reached (Suchecki et al. 2005). Interestingly, a slow-down of the opinion dynamics on the agent level, i.e., a certain reluctance to change the opinion, can lead to a speed up of the opinion dynamics on the systemic level: consensus is reached faster (Stark et al. 2008). Also, the topology of the social network that facilitates agent interactions has an important influence on the consensus formation (Min and San Miguel 2017), as well as possible nonlinear responses to the frequency of opinions (e.g., minority voting, voting against the trend, etc.) (Schweitzer and Behera 2009). Eventually, such models can be extended to include assumptions of social impact theory (Nowak et al. 1990; Lewenstein et al. 1992), such as different weights of opinions, persuasion from agents with different opinions and support from agents with the same opinion (Holyst et al. 2001).
The advantage of this model class is its analytical tractability, in addition to computer simulations, its disadvantage is in the many simplifications made (Schweitzer 2018). More realistic models are based on a continuous characterization of opinions, e.g., as positive real numbers in a given interval, [0, 1]. The most prominent class of such models is the “bounded confidence model” that assumes agents only interact if the difference in their opinions is less than a certain threshold \(\varepsilon\) (Deffuant et al. 2000; Hegselmann and Krause 2002). In this case, agents converge toward the mean of their opinions because of their interactions. The possibility to reach consensus then depends on the value of \(\varepsilon\) (Lorenz 2007). To foster consensus, assumptions about the topology of social interactions (e.g., group interactions) (Meng et al. 2018), hierarchical decisions (Perony et al. 2013), the influence of in-groups (agents known from previous interactions) (Groeber et al. 2009) can be taken into account.
Still, this model class is rather abstract, focusing on effects on the conceptual level. Toward more realistic models, the next step is to consider multi-dimensional opinions (Schweighofer et al. 2020b, a). Usually, individual’s opinions on different subjects are not independent, but show correlations such that, out of a multi-dimensional opinion space, characteristic dimensions, e.g., left-right, conservative-liberal emerge (Schweighofer et al. 2020a). In addition to the simple attractive force assumed in the bounded confidence model (convergence toward the mean), now we have to consider also repulsive forces: agents increase the distance of their opinions as a result of their interaction. In political space, this often leads to polarized opinions (Banisch and Olbrich 2019; Mäs and Flache 2013). Consensus in such scenarios is a rare exception, studies rather focus on the possibility to obtain qualified majorities (Baldassarri and Bearman 2007; Garcia et al. 2012; Bornschier 2015). Such models, while more complex, already allow to capture relations in real-world surveys. They can be further enhanced by including the affective response of individuals and emotional influences (Schweitzer et al. 2020; Schweighofer et al. 2020a), in addition to social ones.
In conclusion, to formally model collective decision processes, we can build on a number of agent-based approaches at different levels of complexity. In this paper, we will use the second model class described above, which uses a continuous opinion representation and a mutual convergence of individual opinions, to describe a particular phenomenon of collective decisions, namely the wisdom of crowds (WoC). It applies to scenarios with factual questions where a true opinion \({\mathcal {T}}\) exists, even if it is not known to individuals (Galton 1907). Our running example: “How long is the border between Switzerland and Italy in kilometers?” (Lorenz et al. 2011) has a true answer (734 km), while individuals usually only have raw estimates. The WoC effect then states that the average over all individual opinions is remarkably close to the true opinion. Hence, it denotes a purely statistical effect but, interestingly, there is a lot of empirical evidence for it (Kittur and Kraut 2008; Ray 2006; Mannes 2009). This is quantified by the small collective error, \({\mathcal {E}}\), which is the squared difference between the average and the true opinion.
According to Surowiecki (2005), four criteria are required to form a wise crowd: diversity of opinions, independence of opinions, some expertise, and the ability to aggregate individual opinions into collective opinions. “Expertise” only refers to the basic ability to give a meaningful answer to the question, e.g., the border of Switzerland is neither 0.1 kilometers, nor 3 million miles. The ability to aggregate implies that someone, e.g., the social planner, indeed has access to all individual opinions, to calculate the aggregate. The other two criteria are more important to us. The diversity of opinions is large only if individuals have independent opinions. But what happens if individuals obtain information about the opinions of others and then have the opportunity to revise their own opinion? This question was investigated in a large empirical study (Lorenz et al. 2011), where individuals had to answer the same question consecutively a number of times, while receiving different information from others. In the so-called aggregated-information regime, they obtained at each time step information about the aggregated opinion of others. In the full-information regime, they instead obtained at each time step information about each individual opinion. These two information regimes allowed them to revise their own opinion accordingly.
The study had two important findings: (i) In the presence of information about the opinions of others, the group diversity of opinions drastically decreased. That means, individuals tried to converge with their opinions, i.e., subjectively they got the impression to reach consensus. (ii) Despite this convergence, the collective error, which measures the distance to the truth, did not decrease, but increased. That means, the group collectively converged to an opinion which was objectively the wrong one. This scenario, which was obtained quite frequently, is very dangerous because the group, converging to a common opinion, was collectively convinced that the wrong opinion was the right one. This effect was stronger in the full-information regime compared to the aggregated-information regime.
To answer the question, under what conditions this will happen, we need an agent-based model that reflects these two different information regimes and further allows to vary the strength of the social influence of other opinions, in comparison to the own conviction. The aim of our paper is to provide such a model, as an extension of the bounded confidence model. In particular, we want to model the full-information regime, which has shown the strongest effects, while the aggregated-information regime is used as a reference case.
The rest of the paper is organized as follows. Section 2 introduces our agent-based model of opinion dynamics and relates it to macroscopic indicators to quantify the WoC effect. Section 3 then presents the results of extensive agent-based simulations with respect to the three macroscopic measures of the wisdom of crowds: the collective error, the group diversity of opinions, and the WoC indicator. Finally, the main conclusions are summarized in Sect. 4.
2 Modeling the wisdom of crowds
2.1 Micro dynamics of opinion formation
With the term “micro dynamics” we refer to the dynamics of the system elements, i.e., the agents. We build on the framework of Brownian agents (Schweitzer 2003), which considers that agents have a continuous internal degree of freedom. In our case, this is the opinion \(x_{i}(t)\), different for each agent \(i=1,\ldots ,N\). We assume that the values of \(x_{i}\) can be mapped to nonzero positive real numbers, i.e., \(x_{i}(t)>0\), but are not bound to a defined interval. This reflects the experimental situations described before (Lorenz et al. 2011).
These opinions can change over time because of influences from other agents or simply because agents change their mind. \(x_{i}(0)\) denotes the initial value. We propose the following general dynamics (Schweitzer 2020):
This dynamics resembles the stochastic equation proposed by Langevin in 1906 to describe Brownian motion. His main idea was the additive superposition of deterministic and stochastic influences. While Brownian particles are physical entities moving in physical space, this idea can be used to describe the stochastic dynamics of agents in any (virtual) space. It has been developed into a modeling framework of Brownian agents (Schweitzer 2003) with applications in various areas, from active matter (Schweitzer 2019) to emotional influence (Schweitzer et al. 2020).
The term \(-\beta x_{i}\) describes, in the absence of other influences, a relaxation process toward zero at a time scale \(\beta\). The term \(S_{i}(t)\) is an additive stochastic force that describes random influences on the dynamics of opinions. We assume that these fluctuations are centered around the initial opinion \(x_{i}(0)\), to reflect the fact that individual convictions about certain subjects are likely to be long-lived. Hence, \(\left\langle S_{i}(t) \right\rangle \propto x_{i}(0)\) up to a constant. We find it more convenient to rewrite the stochastic part as:
\(\mbox{where}\ \xi _{i}(t)\) is a Gaussian white noise, i.e., it is not correlated in time and zero on average, A denotes the strength of the stochastic force and is set equal to all agents.
The term \({\mathcal {F}}_{ij}(t)\) eventually describes how the change of opinion of agent i is influenced by the opinion of other agents j. To better understand its impact, let us first assume \({\mathcal {F}}_{ij}(t)\equiv 0\), i.e., agents do not have any information about the opinions of others. We call this the no-information regime. It implies that agents update their opinions stochastically without considering any other information. With Eqs. (1), (2) the opinion dynamics for this case simply reads:
This stochastic equation denotes a standard Ornstein–Uhlenbeck process which also has an analytic solution (Mavrodiev and Schweitzer 2021). In this case the time average of the individual opinion, \(\overline{x_{i}(t)}\), equals \(x_{i}(0)\) for large t with decreasing variance.
Differently from this trivial case, in this paper we discuss the case that agent i has full information about the opinions of others and can take these into account in weighted manner, to update her own opinion. This is reflected in the following assumption for \({\mathcal {F}}_{ij}(t)\):
That means the social influence from the opinion of other agents increases with the difference between opinions. While this sounds like a simplified assumption, it has been empirically justified in (Mavrodiev et al. 2013); therefore, we use it here.
The coupling variable \(w_{ij}\) is chosen to decay with the difference in opinions (Latane 1981):
with a normalization constant \({\mathcal {N}}_{i}\), such that \(\sum _{j=1}^{N}w_{ij}=1\). The parameter \(\alpha\) acts as a measure of the strength of the social influence in the population. Small values for \(\alpha\) indicate that agents are less susceptible to others’ opinions, even if these opinions are similar. Conversely, large values for \(\alpha\) imply that agents with potentially very different opinions will be able to influence each other, as their susceptibility to social influence is now much higher. In the limit case that \(\left| x_{j}-x_{i} \right|\) can be ignored, which is discussed further below, we see from Eq. (5) that for \(\alpha \rightarrow 0\) also \(w_{ij}\rightarrow 0\), as one would expect. Further, for the relevant range of values \(0.2 \le \alpha \le 0.8\), \(w_{ij}\propto \alpha\).
In summary, the stochastic dynamics for the opinion of agent i in the full information regime becomes:
To make the impact of individual conviction, represented by the second term including \(\beta\), comparable to the impact of social influence, represented by the first term including \(\alpha\), we choose parameter values \(0 \le \alpha \le 1\) and \(1\le \beta \le 2\). The above dynamics does not easily lend itself to analytical treatment; hence, we will simulate it in Sect. 3. But to interpret the results, we first need to think about some comparison.
2.2 Reference scenario
We want to compare our results to a reference case, in which agents have information only about the average opinion of all other agents. We call this the aggregated-information regime (Mavrodiev et al. 2012; Mavrodiev and Schweitzer 2021). In this case the coupling variable \(w_{ij}\) is effectively a constant, equal for all agents: \(w_{ij}\equiv \alpha\). Then, we can express the influence of other opinions as follows:
where \(\left\langle x(t) \right\rangle\) is denoted as the mean opinion in the following. Eq. (7) results in the stochastic dynamics:
Because of the coupling to the mean opinion, this type of opinion dynamics relates to earlier studies that address the averaging of opinions (Degroot 1974; Ganser and Keuschnigg 2018) and the problems related to this (Hogarth 1978). At the same time, our dynamics differs from the opinion dynamics that is assumed in the so-called bounded confidence model (Deffuant et al. 2000) precisely because it does not restrict the interaction of agents to a confidence interval \(\varepsilon\) which denotes the tolerable difference in opinions. Also, the bounded confidence model does not include an individual conviction \(\beta\), nor a dependence on the initial opinion, nor any stochastic influences. For a further discussion about the class of models that include our proposed opinion dynamics as well as the bounded confidence model, we refer to (Schweitzer 2020).
2.3 Macroscopic measures for the wisdom of crowds
To evaluate the outcome of our model, we entirely focus on the systemic properties. Individual trajectories from the experiments can be found in (Lorenz et al. 2011, Fig. 1A). Data about individual estimates have also been shown and analyzed in (Mavrodiev et al. 2013, Fig. 1). These trajectories strongly fluctuate and not allow to deduce useful information. Apart from this restriction, there is also a principle argument. Our paper addresses a collective effect, the wisdom of crowds (WoC). In the presence of social influence, WoC is no longer just a statistical average, it becomes an emergent phenomenon because of the collective interactions of agents. As such, it cannot be decomposed into individual contributions, and we should avoid raising wrong expectations.
Therefore, in this paper, we focus on macroscopic measures to analyze the impact of social influence on the collective level. We remind that WoC is expected to work if the diversity of individual opinions is large, while the deviation of the average opinion from the true value \({\mathcal {T}}\) is small. Therefore, in line with previous studies (Lorenz et al. 2011), we will use the collective error, \({\mathcal {E}}\), the group diversity, \({\mathcal {D}}\), and the wisdom of crowds indicator, \({\mathcal {W}}\), as measures to evaluate these conditions.
In order to define these measures, we need to keep in mind that the distribution of opinions in the considered experimental setup is very broad, and can be proxied by a log-normal distribution. Therefore, the average opinion is not well represented by the arithmetic mean, \(\left\langle x \right\rangle =\sum _{i}x_{i}/N\), but by the geometric mean, which is equivalent to the arithmetic mean of the \(\log\) values, \(\left\langle \ln x \right\rangle\), (Lorenz et al. 2011). Further, because opinions change over time according to Eq. (6), we are only interested in the long-term (LT) values of these macroscopic measures. In a strict mathematical sense long-term is defined as the time when the dynamics reaches a stationary state, i.e., neither the collective error nor the group diversity change. In Sect. 2.4 we give a practical definition for our numerical simulations.
The long-term collective error \({\mathcal {E}}_{\mathrm {LT}}\) shall be defined as the squared deviation of the average opinion from the true value, \({\mathcal {T}}\):
The long-term group diversity \({\mathcal {D}}_{\mathrm {LT}}\) is given by the variance of the distribution of opinions:
The WoC indicator \({\mathcal {W}}\) measures to what extent the truth is bracketed by the opinion distribution. In other words, it indicates how central the position of true value \({\mathcal {T}}\) is within the distribution of opinions.
More formally, we define it as follows. Let \(X_{N}\) be the set of all N opinions. Consider the set of ordered opinions \(\{{\bar{x}}_{i} | {\bar{x}}_{i} \in X_{N}, {\bar{x}}_{i} \le {\bar{x}}_{j}, ~\forall ~i<j\}\). The indicator \({\mathcal {W}}\) is defined as \(\max \{i | {\bar{x}}_{i} \le {\mathcal {T}} \le {\bar{x}}_{N-i+1}\}\). It reaches a maximum of [N/2] when the truth is either the most central opinion or is bracketed by the two most central opinions, and a minimum of 0 when \({\mathcal {T}} \notin ({\bar{x}}_{0},{\bar{x}}_{N})\). To illustrate this, let us assume we have a set of 100 ordered opinions such that \(\{1,2,3,\ldots ,99,100\}\). The two most central opinions in this set are 49 and 50, or 50 and 51, respectively. If the true value would be 50, it is just bracketed by the two most central opinions. This would give us \({\mathcal {W}}=50=N/2\). If the true value would be 70, it is no longer bracketed by the two most central opinions. Instead, it is 20 positions away from the central opinions, hence \({\mathcal {W}}=30\).
2.4 Initial configuration and numerics
In order to perform agent-based simulations using Eqs. (6), (8) we need to specify the initial distribution of opinions, from which N values \(x_{i}(0)\) are sampled. We take as an input two different log-normal distributions \(P^{(1)}(x)\), \(P^{(2)}(x)\) with two different mean values \(\mu ^{(1)}_{\ln x}=-2.9\) and \(\mu ^{(2)}_{\ln x}=-3.0\), but the same variance \(\sigma ^{2}_{\ln x}=0.72\). The histograms of the \(N=100\) opinions sampled from these two initial distributions are plotted in Fig. 1.
Further, we have considered three different true values, \(\ln {\mathcal {T}}={-2.00}\), \(\ln {\mathcal {T}}=-2.90\), \(\ln {\mathcal {T}}=-3.12\). With these values and the parameters of the initial distributions, we can determine the initial collective error \({\mathcal {E}}(0)\) from Eq. (9) and the initial group diversity \({\mathcal {D}}(0)\) from Eq. (10). With these specifications, we run a simulation of \(N=100\) agents in each information regime.
Histograms of initial opinions, \(x_{i}(0)\), sampled from two different log-normal distributions. The blue lines indicate the different mean values \(\mu ^{(1)}_{\ln x}=-2.9\) (left) and \(\mu ^{(2)}_{\ln x}=-3.0\) (right), the variance \(\sigma ^{2}_{\ln x}=0.72\) is the same. Note the logarithmic values of the x-axis (Color figure online)
The dynamics are solved using the 4th order Runge–Kutta method for the full-information regime, Eq. (6), and the Euler method for the aggregated-information regime, Eq. (8). We used a constant time step \(\varDelta t=0.01\). The noise intensity was chosen as a rather small value, \(A=10^{-3}\).
We ran the simulations for \(t=3000\) time steps to approximate long-term behaviour for all quantities of interest in both information regimes. In fact, in Mavrodiev and Schweitzer (2021) we demonstrate that the dynamics of the aggregate regime has an exact solution and converges to a stationary collective error, stationary (nonzero) group diversity and wisdom of crowds indicator. We found that \(t=3000\) time steps is more than enough to ensure convergence to these theoretical values. The dynamics of the full information regime also reaches a stationary state within the numerical precision of our calculations. Hence, we use \(t=3000\) for it as well.
3 Results of agent-based simulations
3.1 Collective error
We present all our results as heat maps of the relevant quantities, \({\mathcal {E}}_{\mathrm {LT}}\), \({\mathcal {D}}_{\mathrm {LT}}\) or \({\mathcal {W}}_{\mathrm {LT}}\), dependent on the two model parameters, social influence, \(\alpha\), and individual conviction, \(\beta\), for which we have performed a thorough parameter sweep. The right column always refers to the full-information regime, the focus of our paper. The left column shows the matching results for the reference case, the aggregated-information regime, which has been discussed in (Mavrodiev et al. 2012) regarding agent-based simulations and in (Mavrodiev and Schweitzer 2021) regarding analytic solutions for the macroscopic measures.
Agent-based simulations of the long-term collective error \({\mathcal {E}}_{\mathrm {LT}}\) (color coded) dependent on the values of social influence \(\alpha\) (x-axis) and individual conviction \(\beta\) (y-axis). Red color corresponds to high collective error (detrimental), while blue corresponds to low collective error (beneficial). (left) Aggregated-information regime, Eq. (8), (right) full-information regime, Eq. (6). Parameters: \(N=100\), \(t=3000\), \(A=10^{-3}\), \(\varDelta t=0.01\). Different initial conditions: (a) \({\mathcal {E}}(0)=0.81\), \(\ln {\mathcal {T}}={-2.00}\), \(\left\langle \ln x(0) \right\rangle =-2.9\), (b) \({\mathcal {E}}(0)=0.014\), \(\ln {\mathcal {T}}=-3.12\), \(\left\langle \ln x(0) \right\rangle =-3.0\), (c) \({\mathcal {E}}(0)=0.01\), \(\ln {\mathcal {T}}=-2.90\), \(\left\langle \ln x(0) \right\rangle =-3.0\). Black contour lines indicate regions in the parameter space where \({\mathcal {E}}_{\mathrm {LT}}={\mathcal {E}}(0)\). Note that these are vertical lines at \(\alpha =0\) in all plots, in (c) there is an additional line (Color figure online)
Figure 2 shows the results for \({\mathcal {E}}_{\mathrm {LT}}\) for three different initial conditions (a)-(c). The color code indicates the value of \({\mathcal {E}}_{\mathrm {LT}}\): (red) for high values, which is detrimental, and (blue) for low values, which is beneficial. We note that for each plot the color code represents different values. A black line indicates parameter combinations \((\alpha ,\beta )\) for which \({\mathcal {E}}_{\mathrm {LT}}={\mathcal {E}}(0)\). Mostly, these lines are not noticeable because they coincide with \(\alpha =0\).
In Figure 2(a), the initial condition is chosen such that the average initial opinion is far away from the true value, i.e., the initial collective error is high. Then, we find that an increase of social influence \(\alpha\) considerably decreases the collective error, which means it improves the wisdom of crowds, whereas individual conviction has little impact on the outcome. This positive finding is much stronger in the full-information regime, in which agents have access to the opinions of all other agents. It decreases if they have access only to the aggregated opinion.
The situation inverts if instead the initial condition is chosen such that the average initial opinion is close to the true value, i.e., the initial collective error is low. Then, an increase in social influence \(\alpha\) can worsen the outcome, leading the average opinion farther away from the true value, as shown in Fig. 2(a). This is the most dangerous case: agents collectively converge to a common opinion, but this, from an objective perspective, is the wrong one. This effect, again, is much stronger in the full-information regime. In the aggregated-information regime, we could still identify parameter ranges with low \(\alpha\), where the wisdom of crowds is not much distorted. But more information for the agents destroys this possibility. Individual conviction, as the second influential parameter, impacts the results mainly for the aggregated-information regime, but is less noticeable in the full-information regime.
This leads us to the question why there is this monotonous deterioration of the wisdom of crowds with increasing social influence. A theoretical investigation of the average opinion \(\left\langle \ln x(t) \right\rangle\) in the aggregated-information regime (Mavrodiev and Schweitzer 2021) tells us that it can only increase over time, \(d \left\langle \ln x(t) \right\rangle /dt >0\). Therefore, if initially \(\left\langle \ln x(0) \right\rangle < \ln {\mathcal {T}}\), there is a chance that \(\left\langle \ln x(t) \right\rangle \rightarrow \ln {\mathcal {T}}\) over time, if \(\alpha\) is large enough and \(\beta\) is not too strong. However, if initially \(\left\langle \ln x(0) \right\rangle > \ln {\mathcal {T}}\), the interaction dynamics of the agents can only lead their average opinion further away from the true value. This is the case shown in Fig. 2(b), and it becomes worse both if social influence increases or if full information about the opinion of others is provided.
Consequently, we should also expect situations without a monotonous deterioration. This is shown in Fig. 2(c), which illustrates a non-monotonous dependence of the collective error on the social influence. Here, the initial collective error is also low, as in (b), but now the initial distribution of opinions is such that \(\left\langle \ln x(0) \right\rangle < \ln {\mathcal {T}}\). Hence, we find that for low values of the social influence the collective opinion indeed converges to the true value (indicated by deep blue). But the parameter range is rather small, and much smaller than in the aggregated-information regime. Hence, we can conclude that for relatively low initial collective error and \(\left\langle \ln x(0) \right\rangle < \ln {\mathcal {T}}\) low levels of social influence can improve the wisdom of crowds, whereas large social influence most likely deteriorates it.
The impact of the second model parameter, individual conviction \(\beta\), becomes more visible for the chosen initial conditions (c). Taking a fixed social influence, e.g., \(\alpha =0.5\), we find that individual conviction can improve the collective error, because it acts as a kind of reluctance against converging to the (wrong) collective opinion.
We also point to the visible black line which indicates the conditions under which the collective error does not change, i.e., is equal to the initial value. In the full-information regime, this is not a straight line as found for the reference case. That means, nonlinear effects become much stronger if agents have access to all other opinions.
3.2 Group diversity
The second macroscopic measure for the wisdom of crowds is shown in Fig. 3, again in comparison to the reference case. Note that the long-term group diversity \({\mathcal {D}}_{\mathrm {LT}}\) does not depend on the initial conditions, but only on \((\alpha ,\beta )\) and the initial group diversity \({\mathcal {D}}(0)\). Therefore, the plot is the same for all initial conditions shown in Fig. 2. The color scale is chosen such that large group diversity, which is generally beneficial for the wisdom of crowds effect, is indicated by red, whereas small group diversity, generally undesirable, is shown in blue. We find that in the full-information regime the group diversity is drastically reduced by means of social influence. Its high initial value cannot be maintained, not even for the case of high initial conviction \(\beta\).
This becomes a problem for those parameter ranges, where a low group diversity is combined with a high collective error. In this case, the agent population collectively converges to the (objectively) wrong opinion. We see that this is most likely the case for the full-information regime, whereas in the reference case the parameter range for \(\alpha\) and \(\beta\) that still maintains relatively high group diversity is larger.
Agent-based simulations of the long-term group diversity \({\mathcal {D}}_{\mathrm {LT}}\) (color coded) dependent on the values of social influence \(\alpha\) (x-axis) and individual conviction \(\beta\) (y-axis). Red color corresponds to large group diversity (beneficial), while blue corresponds to low group diversity (undesirable). (left) Aggregated-information regime, Eq. (8), (right) full-information regime, Eq. (6). Parameters: \(N=100\), \(t=3000\), \(A=10^{-3}\), \(\varDelta t=0.01\). Initial condition: \({\mathcal {D}}(0)=0.72\) (Color figure online)
3.3 WoC indicator
Finally, we discuss the results for the long-term WoC indicator \({\mathcal {W}}_{LT}\), which measures the extent to which the truth is bracketed by the opinion distribution. Ideally, the true value should be central with respect to the opinion distribution. For our configuration with \(N=100\) agents, it would attain the ideal maximum value of \([N/2]=50\).
Figure 4 presents the results for the full-information regime and the reference case, for two different initial conditions (a) and (b). The color code is chosen such that (red) indicates high beneficial values for the WoC indicator, while (blue) corresponds to low values, which are undesirable.
Initial condition in Fig. 4a corresponds to the initial conditions in Fig. 2b. It has a small initial collective error, but the true value \(\ln {\mathcal {T}}\) is smaller than the initial collective opinion \(\left\langle \ln x(0) \right\rangle\). The initial WoC indicator for this starting configuration has the correspondingly moderate value of \({\mathcal {W}}(0)=43.\) Furthermore, in accordance with the discussion of Fig. 2b the collective opinion deviates away from the true value for any nonzero social influence strength \(\alpha\). Hence, the starting configuration in Fig. 4a represents an undesirable initial condition—a moderately unwise initial crowd (\({\mathcal {W}}(0)=43\)) inexorably drifts further and further away from the truth with any amount of social influence.
Initial condition (b), on the other hand, which is the same as in Fig. 2c, is comparably better suited for reaching the true value and correspondingly maximizing the WoC indicator. It has a relatively large \({\mathcal {W}}(0)=46\), i.e., \(\ln {\mathcal {T}}\) is bracketed better by the initial distribution of opinions. This starting configuration also has a small initial collective error, but the true value \(\ln {\mathcal {T}}\) is larger than the initial collective opinion \(\left\langle \ln x(0) \right\rangle\). This means that the collective opinion can possibly converge to the true value with social influence.
Agent-based simulations of the long-term wisdom-of-crowds indicator \({\mathcal {W}}_{\mathrm {LT}}\) (color coded) dependent on the values of social influence \(\alpha\) (x-axis) and individual conviction \(\beta\) (y-axis). Red indicates high beneficial values for the WoC indicator, while blue corresponds to low values, which are undesirable. (left) Aggregated-information regime, Eq. (8), (right) full-information regime, Eq. (6). Parameters: \(N=100\), \(t=3000\), \(A=10^{-3}\), \(\varDelta t=0.01\). Different initial conditions: (a) \({\mathcal {W}}(0)=43\), \({\mathcal {E}}(0)=0.02\). (b) \({\mathcal {W}}(0)=46\), \({\mathcal {E}}(0)=0.01\). Both: \(\left\langle \ln x(0) \right\rangle =-3.0\), \({\mathcal {D}}(0)=0.72\) (Color figure online)
Still, as we illustrate in Fig. 4, the more favorable initial condition (b) does not automatically lead to a better wisdom of crowds. This is due to the opinion dynamics fully controlled by the parameters \((\alpha ,\beta )\). Because of the interplay between social influence \(\alpha\) and individual conviction \(\beta\), agents change their opinions such that (i) the final opinion distribution becomes more narrow, and (ii) the mean \(\left\langle \ln x_{\mathrm {LT}} \right\rangle\) shifts toward higher values. How far it shifts depends on these two social parameters.
The parameter dependence displayed in Fig. 4 shows that in most cases an increasing social influence \(\alpha\) leads to a decreasing WoC indicator (blue region). This effect again becomes much stronger in the full-information regime than in the reference case. As a counter-balance increasing individual conviction is able to mitigate the deterioration. For the initial condition (b), we observe a non-monotonous dependence of \({\mathcal {W}}_{\mathrm {LT}}\) on the strength of the social influence, very similar to the dependence shown in Fig. 2(c) for the collective error. In this case, rather small values of \(\alpha\) enhance the chance to converge to the true value, which is shown by a high WoC indicator. Higher values of \(\beta\) are able to strengthen this effect, enlarging the favorable red region in Fig. 4(b), even in the full-information regime.
We can conclude that for both the collective error, Fig. 2, and the WoC indicator, Fig. 4, we find the same parameter regions where social influence can be beneficial for the wisdom of crowds. Provided suitable initial conditions, the collective opinion can even converge to the true value, indicated by the minimum collective error, \({\mathcal {E}}_{\mathrm {LT}}=0,\) and the maximum WoC indicator, \({\mathcal {W}}_{\mathrm {LT}}=[N/2]=50\). Despite the loss of group diversity, shown by low values of \({\mathcal {D}}_{\mathrm {LT}}\) in Fig. 3, the crowd becomes “wiser” for moderate values of the social influence. It is non-trivial and interesting to see that all observed effects are much stronger in the full-information regime, in comparison to the reference case. Because the opinion dynamics is quite sensitive to the available information, the parameter ranges for a favorable outcome considerably decrease in the presence of stronger agent interactions, i.e., in the full-information regime.
4 Conclusion
The wisdom of crowds refers to cases in which a large number of individuals has an opinion about a question for which a true answer exists, although this is not public knowledge. Then, it was observed already by Galton in 1907 (Galton 1907) that the average opinion is remarkably close to the true opinion. This works best if the diversity of individual opinions is large and all opinions are independent. In most real-world scenarios, however, individuals become aware of the opinions of others and then tend to adjust their own opinion based on this information, which can be seen as a social influence from others.
In the presence of social influence, the wisdom of crowds is no longer just a statistical average, it becomes an emergent phenomenon because of the mutual influence between individuals. To analyze the impact of social influence on the collective level, we need aggregated measures, three of which are calculated in this paper, namely the collective error, group diversity and WoC indicator.
To obtain these aggregated measures, we have proposed an agent-based model that reflects two competing influences: (i) the individual conviction about the own initial opinion (parameter \(\beta\)), (ii) the influence of the opinions of others (parameter \(\alpha\)). The latter reflects a mutual social influence via the exchange of information. Two different regimes are considered: a full-information regime in which agents get to know the opinion of each other agent, and an aggregated-information regime in which agents only get to know the average opinion. The model assumes that agents have a stronger incentive to adjust their opinion if the difference to other opinions, or to the average opinion, is larger. This is reasonable: if someone thinks the length of the border between Switzerland and Italy is 500 km and then sees many opinions with values between 2000 and 3000 km, there is a stronger “force” to adapt to the majority (even if this is wrong: the true value is 734 km). This type of adaptation has already been confirmed by experiments (Lorenz et al. 2011; Mavrodiev et al. 2013). Hence, social influence eventually leads to a decreasing group diversity of opinions. This is perceived as converging to some sort of consensus, which likely gives more confidence in the outcome of the collective decision process.
Unfortunately, as the mentioned experiments (Lorenz et al. 2011; Mavrodiev et al. 2013) have also shown, because of this convergence crowds become easily convinced that their collective opinion is also the right one, even if it is objectively wrong. Thus, the main objective of our paper is to understand under which conditions this distorted wisdom of crowds could emerge. Our agent-based model plays a valuable role in systematically evaluating these conditions (a) regarding the parameters involved, and (b) regarding the impact of the initial conditions.
Our results demonstrate that the role of social influence cannot be reduced to simplistic conclusions. Instead, they reflect that collective opinion dynamics, as most social processes, are more complex. Specifically, we do find scenarios in which social influence is beneficial for the wisdom of crowds, as in Fig. 2a, c. But as illustrated in the figure, these scenarios are heavily dependent on the initial average opinion and the position of the true value with respect to it. The positive effect quickly reverses if either condition changes, as shown in Fig. 2b. It is this dependency of the WoC effect on the initial conditions that we regard as critical, because, under practical circumstances, these initial conditions are unknown. This means, we cannot have a-priori knowledge of whether social influence will enhance or distort the WoC. To ensure steady collective improvement one needs to regularly re-evaluate the crowd performance, rather than fixing social mechanisms and policies a-priori.
With these insights we distinguish our work from other studies such as (Kao et al. 2018), where the focus is on correcting group estimates. This requires to collect enough training data from the same decision-making domain, which is not always possible. We do not presume that enough decision-making history is available to take any corrective actions, and we do not want to correct estimates. Instead, we show that social influence is not unilaterally detrimental for the wisdom of crowds, an insight that is not considered in many empirical or theoretical works in this field.
Our insights help to explain the “range reduction effect” found empirically Lorenz et al. (2011). Because of the adjustment of individual opinions, the opinion distribution, in particular its mean and its median shifts over time such that the true opinion is displaced to peripheral regions of the opinion distribution, while the collective opinion becomes narrowly centered around a wrong value. This generates a dangerous situation because relying on the average opinion in this case would give the wrong information. Our investigations show the range of parameters \((\alpha ,\beta )\) and the necessary initial configuration of the crowd (in terms of collective error and group diversity), where social influence generates such an outcome, effectively distorting the wisdom of crowds.
Comparing the full-information regime with our reference case, the aggregated-information regime, we note that all effects are much stronger if the information about the opinions of all agents becomes available. Individual conviction could counterbalance the social influence, but plays a lesser role. This is also understandable: in the full-information regime, someone not only realizes the differences in opinions, in comparison to the own one, but also how many other individuals deviate from it. This is hidden in the aggregated-information regime, where someone only knows the difference to the average opinion; hence, its impact may be smaller from a psychological perspective.
One could rightly argue against the latter point, because the wisdom of crowds only works with respect to the average opinion which should be close to the true opinion. So, someone with a basic understanding of the wisdom of crowds should find the average opinion much more reliable, and influential, than knowing all other opinions. This argument ignores one main point: the wisdom of crowds only works if we have a large number of independent opinions. Only then, the average opinion may generate the better signal. Once individuals get to know other opinions, their opinions are no longer adjusted independently, but in response to the social influence generated. Hence, even a small social influence has the potential to distort the wisdom of crowds, as it was found in experiments and confirmed by our agent-based simulations.
References
Baldassarri, D., & Bearman, P. (2007). Dynamics of political polarization. American Sociological Review, 72(5), 784–811.
Banisch, S. (2014). From Microscopic heterogeneity to macroscopic complexity in the contrarian voter model. Advances in Complex Systems, 17(5), 1450025.
Banisch, S., & Olbrich, E. (2019). Opinion polarization by learning from social feedback. Journal of Mathematical Sociology, 43(2), 76–103.
Bornschier, S. (2015). The new cultural conflict, polarization, and representation in the swiss party system, 1975–2011. Swiss Political Science Review, 21(4), 680–701.
Bose, T., Reina, A., & Marshall, J. A. (2017). Collective decision-making. Current Opinion in Behavioral Sciences, 16, 30–34.
Castellano, C., Fortunato, S., & Loreto, V. (2009). Statistical physics of social dynamics. Reviews of Modern Physics, 81(2), 591.
Deffuant, G., Neau, D., Amblard, F., & Weisbuch, G. (2000). Mixing beliefs among interacting agents. ACS - Advances in Complex Systems, 3, 87–98.
Degroot, M. H. (1974). Reaching a consensus. Journal of the American Statistical Association, 69(345), 118–121.
Dornic, I., Chaté, H., Chave, J., & Hinrichsen, H. (2001). Critical coarsening without surface tension: The universality class of the voter model. Physical Review Letters, 87(4), 045701.
Fernández-Gracia, J., Suchecki, K., Ramasco, J. J., San Miguel, M., & Eguíluz, V. M. (2014). Is the voter model a model for voters? Physical Review Letters, 112(15), 158701.
Flache, A., Mäs, M., Feliciani, T., Chattoe-Brown, E., Deffuant, G., Huet, S., et al. (2017). Models of social influence: Towards the next frontiers. Journal of Artificial Societies and Social Simulation, 20(4), 2.
Galton, F. (1907). Vox Populi. Nature, 75(1949), 450–451.
Ganser, C., & Keuschnigg, M. (2018). Social influence strengthens crowd wisdom under voting. Advances in Complex Systems, 21(06n07):1850013.
Garcia, D., Mendez, F., Serdult, U., & Schweitzer, F. (2012). Political polarization and popularity in online participatory media : An integrated approach. In Proceedings of the 1st Workshop on Politics, Elections and Data - PLEAD ’12, pp. 3–10.
Groeber, P., Schweitzer, F., & Press, K. (2009). How groups can foster consensus: The case of local cultures. Journal of Aritificial Societies and Social Simulation, 12(2):4 (1–22).
Hegselmann, R., & Krause, U. (2002). Opinion dynamics and bounded confidence models, analysis, and simulation. Journal of Artificial Societies and Social Simulation, 5, 3.
Hogarth, R. M. (1978). A note on aggregating opinions. Organizational Behavior and Human Performance, 21(1), 40–46.
Holyst, J., Kacperski, K., & Schweitzer, F. (2001). Social impact models of opinion dynamics. Annual Reviews of Computational Physics, 9, 253–273.
Kao, A. B., Berdahl, A. M., Hartnett, A. T., Lutz, M. J., Bak-Coleman, J. B., Ioannou, C. C., et al. (2018). Counteracting estimation bias and social influence to improve the wisdom of crowds. Journal of The Royal Society Interface, 15, 20180130.
Kittur, A. & Kraut, R.E. (2008). Harnessing the wisdom of crowds in wikipedia: quality through coordination. In Proceedings of the 2008 ACM conference on Computer supported cooperative work, CSCW ’08, pp 37–46, New York, NY, USA. ACM.
Latane, B. (1981). The psychology of social impact. American Psychologist, 36(4), 343–356.
Lewenstein, M., Nowak, A., & Latané, B. (1992). Statistical mechanics of social impact. Physical Review A, 45, 703–716.
Lorenz, J. (2007). Continuous opinion dynamics under bounded confidence: A survey. International Journal of Modern Physics C, 18(12), 1819–1838.
Lorenz, J., Rauhut, H., Schweitzer, F., & Helbing, D. (2011). How social influence can undermine the wisdom of crowd effect. Proceedings of the National Academy of Sciences of the United States of America, 108(22), 9020–9025.
Mannes, A. E. (2009). Are we wise about the wisdom of crowds? The use of group judgments in belief revision. Management Science, 55(8), 1267–1279.
Mäs, M., & Flache, A. (2013). Differentiation without distancing explaining bi-polarization of opinions without negative influence. PloS ONE, 8(11), e74516.
Mavrodiev, P., & Schweitzer, F. (2021). The ambiguous role of social influence on the wisdom of crowds: An analytic approach. Physica A, 567, 125624.
Mavrodiev, P., Tessone, C.J., & Schweitzer, F. (2012). Effects of social influence on the wisdom of crowds. In Proceedings of the Conference on Collective Intelligence CI-2012. arXiv:1204.2991.
Mavrodiev, P., Tessone, C. J., & Schweitzer, F. (2013). Quantifying the effects of social influence. Scientific Reports, 3, 1360.
Meng, X. F., Van Gorder, R. A., & Porter, M. A. (2018). Opinion formation and distribution in a bounded-confidence model on various networks. Physical Review E, 97(2), 022312.
Min, B., & San Miguel, M. (2017). Fragmentation transitions in a coevolving nonlinear voter model. Scientific Reports, 7(1), 1–9.
Nowak, A., Szamrej, J., & Latané, B. (1990). From private attitude to public opinion: A dynamic theory of social impact. Psychological Review, 97, 362–376.
Perony, N., Pfitzner, R., Scholtes, I., Tessone, C. J., & Schweitzer, F. (2013). Enhancing consensus under opinion bias by means of hierarchical decision making. Advances in Complex Systems, 16(06), 1350020.
Ray, R. (2006). Prediction markets and the financial “wisdom of crowds”. Journal of Behavioral Finance, 7(1), 2–4.
Schweighofer, S., Garcia, D., & Schweitzer, F. (2020a). An agent-based model of multi-dimensional opinion dynamics and opinion alignment. Chaos, 30(9), 093139.
Schweighofer, S., Schweitzer, F., & Garcia, D. (2020b). A weighted balance model of opinion hyperpolarization. Journal of Artificial Societies and Social Simulation, 23(3), 5.
Schweitzer, F. (2003). Brownian Agents and Active Particles. Collective Dynamics in the Natural and Social Sciences. Berlin: Springer.
Schweitzer, F. (2018). Sociophysics. Physics Today, 71(2), 40–46.
Schweitzer, F. (2019). An agent-based framework of active matter with applications in biological and social systems. European Journal of Physics, 40(1), 014003.
Schweitzer, F. (2020). The law of proportionate growth and its siblings: Applications in agent-based modeling of socio-economic systems. In H. Aoyama, Y. Aruka, & H. Yoshikawa (Eds.), Complexity, Heterogeneity, and the Methods of Statistical Physics in Economics, chapter 8 (pp. 145–176). Tokyo: Springer.
Schweitzer, F., & Behera, L. (2009). Nonlinear voter models: The transition from invasion to coexistence. The European Physical Journal B, 67(3), 301–318.
Schweitzer, F., Krivachy, T., & Garcia, D. (2020). An agent-based model of opinion polarization driven by emotions. Complexity, 2020, 5282035.
Stark, H. U., Tessone, C. J., & Schweitzer, F. (2008). Slower is faster: Fostering consensus formation by heterogeneous inertia. Advances in Complex Systems, 11(04), 551–563.
Suchecki, K., Eguíluz, V., & San Miguel, M. (2005). Voter model dynamics in complex networks: Role of dimensionality, disorder, and degree distribution. Physical Review E, 72(3), 36132.
Surowiecki, J. (2005). The Wisdom of Crowds. Anchor.
Funding
Open access funding provided by Swiss Federal Institute of Technology Zurich.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Mavrodiev, P., Schweitzer, F. Enhanced or distorted wisdom of crowds? An agent-based model of opinion formation under social influence. Swarm Intell 15, 31–46 (2021). https://doi.org/10.1007/s11721-021-00189-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11721-021-00189-3